基于改进粒子群算法的支持向量机遥感影像分类
姜 雯,吴 陈
(江苏科技大学 计算机学院,镇江 212100)
遥感影像分类是遥感应用的基础,而影响分类精度的关键在于选择合适的分类方法.支持向量机在小样本、非线性以及高维度的数据分类中具有显著优势,因此适用于复杂的遥感影像分类[1-3].在支持向量机模型中,惩罚因子C和核参数γ是影响分类结果的主要因素[4].人工智能算法[5-7]为启发式算法,即不用去遍历解空间里的所有位置,就可以寻找到问题的最优解,从而能够高效地寻找到最优的支持向量机(support vector machine,SVM)参数.文中采用粒子群算法(particle swarm optimization,PSO)来优化SVM参数,提高SVM的分类性能.粒子群算法是一种基于种群的全局优化方法,具有算法简单,易于实现以及收敛速度快的优点,但在演化过程中很容易过早收敛并陷入局部最优,因此很多学者提出对粒子群算法进行优化[8-11].传统的粒子群算法在优化支持向量机时存在着易陷入局部最优,分类精度低以及早熟收敛的缺点,文中从两个方面对粒子群算法进行优化:一方面,采用自适应权重代替传统的惯性权重来平衡粒子的全局和局部搜索能力;另一方面,引入模拟退火算法对粒子群算法进行优化,使得粒子以一定概率接受较差的解,从而跳出局部最优解,达到全局最优.文中利用改进后的粒子群算法找到最优SVM参数,并将其运用到遥感领域,提高遥感影像的分类精度.
1 支持向量机
支持向量机的原理是建立一个最优分类超平面,并使其在正确分开不同类别的样本的同时,还能分类间隔最大化.当样本线性不可分时,可以利用非线性映射,将低维空间的数据映射到高维特征空间,使得样本在高维特征空间中线性可分,即找到非线性变换:
φ:x∈Rn→φ(x)∈Rmm>p
(1)
假设训练样本集为:
D={(x1,y1),(x2,y2),…,(xl,yl)}
yi∈{+1,-1}i=1,2,…,l
可求得最优分类超平面为:
s.tyi(wTφ(xi)+b)≥1-ξi
ξi≥0,i=1,2,…,l
(2)
式中:w为超平面法向量;ξi为松弛因子;C为惩罚因子;xi为第i个样本的特征;yi为类别标签;φ(xi)为映射函数.
将数据映射到高维特征空间,可解决优化问题:
(3)
由于特征空间的维度较高,为了避免“维度灾难”,引入核函数[12]:
K(Xi,Xj)=(φ(Xi)·φ(Xj))
(4)
将原优化问题转换为:
(5)
式(5)的最优化函数为:
式中:αi为Lagrange乘子;文中采用高斯核函数[12]作为SVM模型中的核函数,其数学形式为:
K(xi,xj)=exp(-γ‖xi-xj‖2)
(6)
式中:γ为核参数.
2 改进的粒子群算法
2.1 标准粒子群算法
粒子群算法是由Eberhart和Kennedy在1995年提出的一种群智能优化算法[13],假设所求解问题的空间是d维,种群大小为m,种群中的每个粒子代表一个可行解,则第i个粒子的位置和速度分别为Xi=(xi1,xi2,…,xid)和Vi=(vi1,vi2,…,vid).记第i个粒子经过的最好位置为pbest=(ppbest,1,ppbest,2,…,ppbest,d),整个种群经过的最优位置为gbest=(pgbest,1,pgbest,2,…,pgbest,d).在迭代过程中,粒子可通过个体极值pbest和群体极值gbest来更新速度和位置,即:
(7)
(8)
式中:w为惯性权重;c1,c2为学习因子,为常数;r1,r2为[0,1]区间内的随机数;k为进化的代数,1≤i≤m,1≤j≤d.
2.2 自适应权重优化粒子群算法
惯性权重w的大小影响粒子群算法在求解过程中的搜索能力.若w较大,则有利于提高粒子的全局最优能力,使得算法跳出局部最优点;若w较小,则会提高粒子的局部最优能力,使得算法趋于收敛.文中采用自适应权重[14-15]来取代惯性权重,从而平衡粒子的全局和局部最优能力:
(9)
式中:wmax为权重的最大值,wmin为权重的最小值,通常取wmax=0.9,wmin=0.4;fi为第i个粒子的适应度值,favg为种群平均适应度值,fg为种群最优适应度值.
将每个粒子的位置变量设定为二维,分别对应SVM的惩罚因子C和核参数γ,用粒子的适应度值来评价粒子所处位置的好坏程度.利用台湾林智仁教授开发的LIBSVM工具箱里的svmtrain函数来计算各个粒子的适应度值.具体计算:
model=svmtrain(train-label,train,cmd)
cmd=[′-v′,num2str(v),′-c′,num2str(x(i,1)),
′-g′,num2str(x(i,2))]
f(i)=model
式中:v为交叉验证数;c为惩罚因子C;g为核参数γ;f(i)为第i个粒子在当前位置的适应度值,算法中用fi表记;train-label为训练数据集标签;train为训练数据集;model为训练得到的支持向量机模型,是一个结构体,但是如果参数配置cmd中用到-v,得到的就不是结构体了,而是交叉验证下的平均分类准确率,即粒子的适应度值.
文中将数据集按照一定的比例划分为训练集和测试集,利用LIBSVM工具箱在训练集中使用三折交叉验证,获得最高分类准确率SVM参数组合,并将最优参数组合的SVM模型对测试集进行预测,最终得到测试集的分类准确率.
自适应权重优化粒子群(WPSO-SVM)算法步骤如下:
步骤1 初始化PSO的相关参数.在一定范围内随机生成粒子的初始位置,每个粒子的初始位置的两个分量分别为x(i,1)和x(i,2).其中,x(i,1)的范围为(Cmin,Cmax),x(i,2)的范围为(γmin,γmax).
步骤2 计算粒子的适应度值.将每个粒子的位置分量x(i,1)和x(i,2)代入适应度函数中得到适应度值.
步骤3 根据粒子初始适应度值,可得到粒子的个体极值pbest和群体极值gbest.
步骤4 根据式(9)更新权重;根据式(7)和式(8)更新粒子的速度和位置.
步骤5 计算粒子当前适应度值,更新粒子个体极值pbest和群体极值gbest.
步骤6 判断是否达到最大迭代次数,若满足则转至步骤7,否则转至步骤2.
步骤7 输出种群最优位置(对应SVM的惩罚因子C和核参数γ).
步骤8 输入最佳参数,进行分类.
2.3 模拟退火算法优化粒子群算法
模拟退火(simulated annealing,SA)算法[16]在搜索过程中不仅接受比当前解更好的解,也会以一定的概率接受较差解.SA算法在搜索过程中具有一定突跳概率[17],可跳出局部最优解,最终达到全局最优.文中采用带压缩因子的PSO算法来选取合适的参数,确保PSO算法能够有效收敛.粒子的速度和位置可更新为:
(10)
(11)
式中:压缩因子
(12)
为了提高PSO算法全局最优的能力,在所有pi中选取一个位置,来替代公式中的gbest.文中采用轮盘赌策略来确定pi,则粒子的速度公式可更新为:
(13)
式中:g′best为选中的粒子.
由于选取的粒子g′best是比gbest差的一个特殊解,因此要选取性能较好的粒子来进行替代gbest.可计算在温度t时,pi相对于gbest的突跳概率为:
(14)
式中:N为种群大小,f为适应度值.
SAPSO算法步骤如下:
步骤1 初始化PSO相关参数(参数设置同WPSO-SVM算法),设置初始温度.
步骤2 计算粒子的适应度值(方法同WPSO-SVM算法, 即2.2节中算法步骤2).
步骤3 根据粒子的初始适应度值,可得到粒子的个体极值pbest和群体极值gbest.
步骤4 根据轮盘赌策略,确定gbest的替代值g′best,根据式(13)和式(11)更新粒子的速度和位置.
步骤5 计算粒子当前适应度值,更新粒子的个体极值pbest和群体极值gbest.
步骤6 进行退火操作.
步骤7 判断是否达到最大迭代次数,若满足则转至步骤8,否则转至步骤2.
步骤8 输出种群最优解(对应SVM的惩罚因子C和核参数γ).
步骤9 输入最佳参数,进行分类.
3 实验结果与分析
3.1 算法验证
文中采用UCI数据库中的Seeds和Wine数据集对改进的算法进行验证分析.Seeds数据集共有3个类别,210个样本.将Seeds数据集的每个类别随机抽取40组数据作为训练集,剩余的90个样本数据作为测试集.Wine 数据集共有3个类别,178个样本.将Wine 数据集的178个样本按照一定比例随机抽取108个训练样本和70个测试样本.
分别用PSO-SVM算法和改进的WPSO-SVM及SAPSO-SVM算法进行MATLAB仿真实验.表1和表2分别记录了测试集中每个类别的错分数目(1、2、3)、总错分数目(总)、算法在训练集上的交叉验证的准确率(CV)以及算法在测试集上的分类精度.结果表明,改进的WPSO-SVM和SAPSO-SVM算法分类精度均优于PSO-SVM,其中WPSO-SVM的分类精度最优.
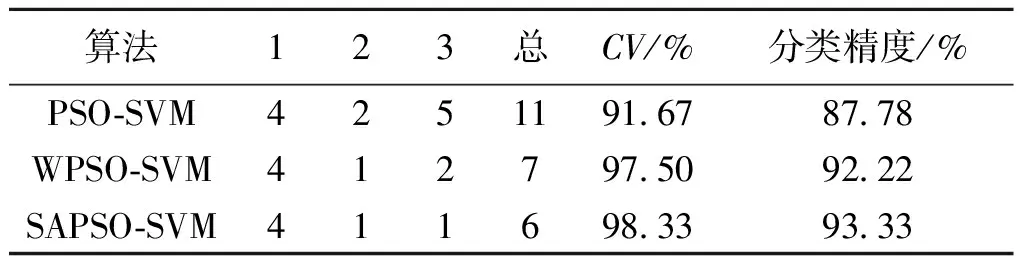
表1 Seeds数据集实验结果Table 1 Seeds experimental result

表2 Wine数据集实验结果Table 2 Wine experimental result
3.2 遥感影像分类
3.2.1 实验一
选取江苏科技大学东校区在2017年4月14日获取的遥感数据作为实验数据,图像的像素大小为450×350,实验区主要包括7个类别,分别为草地、树木、操场、建筑物、水体、道路和阴影.图1为实验区的遥感影像.
参数设置如下,种群进化次数为200,种群数量为20,学习因子c1=1.5,学习因子c2=1.7,惯性权重wmax=0.9,wmin=0.4,SVM参数C的范围为0.01~100,核参数r的范围为0.01~10.实验操作系统为Windows 7,编译软件为Matlab R2014a,硬件为Inter(R) Core (TM) i5-2450M CPU @2.50GHz.

图1 江苏科技大学遥感影像Fig.1 Jiangsu University of Science and Technologyremote sensing image
实验选取了1 800个样本作为训练集,首先在训练集上进行三折交叉验证,找到平均分类准确率最高的SVM参数组合,又随机选取了520个样本作为测试集,最后使用最优参数组合的SVM模型对测试集进行预测,并采用分类混淆矩阵对分类结果进行精度评价.训练集和测试集的具体样本数量如表3,实验结果如表4,5和6.
从表4可以看出,PSO-SVM算法对水体和操场的分类效果较好,均达到了90%以上,但对建筑物和道路的分类较差,部分建筑物被误认为是道路和树木,部分道路被误认为是建筑物和草地.从表4可以看出,WPSO-SVM算法对建筑物和道路的分类效果得到了提升,WPSO-SVM的分类精度相较于PSO-SVM算法提高了2.12%.从表5可以看出,SAPSO-SVM算法的分类精度要优于WPSO-SVM算法,WPSO-SVM算法相较于PSO-SVM算法分类精度提高了2.89%.综上所述,WPSO-SVM算法和SAPSO-SVM算法在一定程度上提高了遥感图像的分类精度.

表3 数据集1Table 3 Dataset 1

表4 PSO-SVM分类混淆矩阵Table 4 PSO-SVM classification confusion matrix

表5 WPSO-SVM分类混淆矩阵Table 5 WPSO-SVM classification confusion matrix

表6 SAPSO-SVM分类混淆矩阵Table 6 SAPSO-SVM classification confusion matrix
3.2.2 实验二
为了进一步验证算法的有效性,选取了苏州工业园区在2017年7月28日获取的遥感数据作为实验数据.实验区图像的像素大小为460×300,实验区主要包括7个类别,分别为树木、居民区、湖泊、广场、裸地、建筑物和阴影.图2为实验区的遥感影像.实验步骤以及实验参数设置同实验一,测试集以及训练集具体设置如表7,实验结果如表8.从表8可以看出,WPSO-SVM和SAPSO-SVM的分类精度均优于PSO-SVM,其中WPSO-SVM的分类精度提高了4.33%,SAPSO-SVM的分类精度提高了3.67%.

图2 苏州工业园区遥感影像Fig.2 Suzhou industrial park remote sensing image

表7 数据集2Table 7 Dataset 2

表8 分类精度评价Table 8 Classification accuracy evaluation
4 结论
(1) 针对粒子群算法在优化SVM参数时易陷入局部最优的问题,文中提出了WPSO-SVM算法和SAPSO-SVM算法,WPSO-SVM算法引入自适应权重进行优化,使得粒子的全局和局部优化能力能达到良好的平衡,避免了粒子早熟收敛.
(2) SAPSO-SVM算法引入SA算法进行优化,赋予粒子一定的突跳概率,能够跳出局部最优解,从而达到全局最优.
(3) 通过UCI数据集和遥感影像进行实验论证,结果表明,文中提出的WPSO-SVM和SAPSO-SVM两种算法相较于PSO-SVM算法能够更容易提取地物特征,提高了遥感影像的分类精度.

