基于故障分量的系统侧谐波阻抗计算方法

卿俊杰李官宇张择策曾 雪令狐静波陈子阳李媛媛

(1.国网成都供电公司，四川 成都 610041；2.国网西藏电力科学研究院，西藏 拉萨 850000)

0 引 言

随着社会经济的发展，电网规模越来越大，并朝着更智能、更坚强的方向发展，这对电力系统的电能质量也提出了更高的要求。而电力系统中的谐波问题是影响电能质量的主要原因之一。电气化铁路是电力系统内最大的三相不平衡谐波源，除此之外还有数量庞大的变频装置、整流装置、电弧炉等非线性负荷，它们会使电压、电流波形产生畸变，对系统造成谐波污染。

只有正确、科学地区分谐波污染责任，才能为系统侧和用户侧的谐波治理提供依据。评估公共耦合点(point of common coupling，PCC) 用户谐波发射水平是谐波污染责任划分的前提，而获得用户谐波发射水平的关键在于准确地计算系统侧的谐波阻抗，这也是国内外研究的热点和难点[1-4]。

系统侧和用户侧的等效电路模型是评估PCC 处谐波污染最常用的工具[5-8]。计算系统侧谐波阻抗的方法主要分为干预式方法[9-11]和非干预式方法[12-17]。其中干预式方法会干扰电力系统，因此误差较大，比如通过投切电容器来实现谐波阻抗的计算；非干预式方法则更为科学，被大多数研究人员采用，计算原理也更为多样。波动量法是最为常用的非干预式方法[18]，利用 PCC 处电压和电流波动量比值的符号进行判别，但该方法需要假设谐波电压波动的主导侧，因此不能保证计算精度。二元线性回归方法基于在PCC处采集的电流和电压，将其进行快速傅里叶变换并提取谐波分量，根据电路理论推导回归方程求取谐波阻抗。然而，该方法仅适用于背景谐波变化不大的情况时，当背景谐波变化很大时，系统侧谐波阻抗的计算将出现较大的估计误差。文献[19]介绍的极大似然估计法是以系统中的背景谐波服从正态分布为前提来求解似然方程，最后计算得出系统侧谐波阻抗值，而显然在实际的电力系统中，背景谐波并不服从标准的正态分布。为了减少了背景谐波的干扰，文献[20]基于独立随机矢量协方差等于0的特点，提出了随机独立矢量法，但该方法在系统侧谐波发射水平变高的情况下，误差也会随之变大。文献[21]介绍了基于贝叶斯理论的系统侧谐波阻抗计算，可以较为准确地计算背景谐波在非正态分布情况下的谐波阻抗，但仍需假设阻抗在估计时间段内不产生突变以及阻抗的先验分布是区间上的均匀分布。

无论是干预式或者非干预式的方法，都是在稳态下进行分析和建模，它们的区别主要在于对数据处理的假设和方法不同。下面，着眼于计算系统侧谐波阻抗的核心目标，研究故障状态下PCC处谐波电压波动与系统及用户侧的电气量关系，提出基于故障分量的系统侧谐波阻抗计算方法。仿真分析表明，无论背景谐波是否视为服从正态分布，采用所提方法都可以较为准确地计算系统侧的谐波阻抗值。所提出的基于故障分量的系统侧谐波阻抗计算方法是对用户侧故障状态下PCC处电气量分析的积极探索，是对快速准确计算具有工程意义的系统侧谐波阻抗的有益尝试，对评估用户谐波发射水平以及划分谐波污染责任有一定指导作用。

1 基本原理

1.1 谐波污染等效分析模型

谐波分析通常采用诺顿等效电路[1-5]，如图1所示。

图1 系统侧和用户侧谐波分析等效电路

根据诺顿定理可列写出等效电路方程为

(1)

文献[14]定义了PCC 点谐波波动伏安特性比KhVA，它实际表征了谐波伏安特性曲线的斜率。通过PCC处的谐波电压、电流波动量的比值来进一步分析系统侧谐波阻抗与两侧电流波动量的关系，如式(2)所示。若仅有系统侧或用户侧的波动引起PCC 点谐波波动时，KhVA的计算变换为式(3)。

(2)

(3)

1.2 用户侧故障状态下PCC电气量分析

1.3 基于故障分量的系统侧谐波阻抗计算

用户侧发生故障的一般情况如图2所示。

图2 用户侧发生故障的一般情况

表1 不同时间段影响PCC处谐波波动量的因素

2 仿真分析

根据图1和图2，使用PSCAD搭建10 kV系统仿真模型，用4种方法(方法1为基于快速独立分量分析的系统侧谐波阻抗计算方法；方法2为二元回归法；方法3为基于贝叶斯定理的系统谐波阻抗估计；方法4为所提方法)，对该10 kV仿真系统的典型谐波(3次、5次、7次、9次、11次、13次谐波)进行测量计算，并对结果误差进行对比分析。

图3 10 kV系统仿真模型

仿真模型设置的系统侧阻抗为ZS=0.5+j1，在负荷侧加入±5%的随机正弦波动。针对所提方法，在PCC点处设置两相接地短路故障，搭建接地电弧模型，随着接地电弧电阻不断变化，从而向系统中注入谐波。

在PCC处提取10 000个仿真数据，每100个数据为一个数据段，进行递推归算。

2.1 基于PSCAD建模的电弧电阻模型

所采用的电弧电阻模型能够准确、有效地反应10 kV系统短路接地时电弧电阻的特性[22]，电弧电压畸变明显，且与实际变电站的故障录波波形相符合，如图4所示。

电弧电导的非线性数学表达式为

(4)

式中：g为电弧电导；τs为时间常数；Gs为稳态电导；β为常量系数；Is为10 kV系统接地故障稳态电流；ih为电弧电流；Vs0为弧隙每厘米压降的常量系数；l为电弧长度。根据现场实际取β=7.53×10-6，Vs0=75 V/cm，l=5 cm。

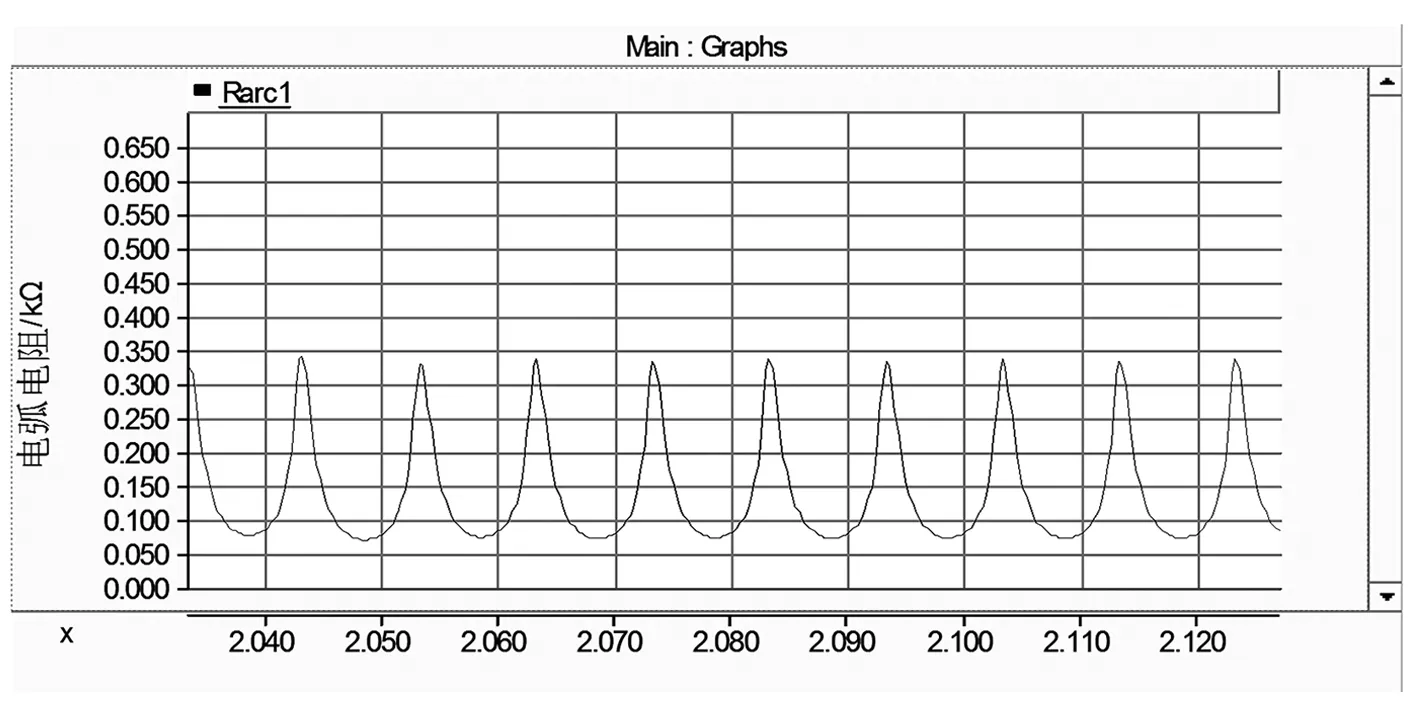
图4 接地电弧电阻仿真结果

2.2 系统谐波阻抗测量

2.2.1 正态背景谐波

负荷侧加入±5%的随机正弦扰动，并且设置为正态随机扰动，提取10 000个仿真数据，分别利用方法1、2、3、4进行数据处理分析；设置10 kV两相短路接地故障，提取故障2个周波后10 000个仿真数据以及短路前两个周波的10 000个仿真数据，利用故障分量进行数据处理分析及谐波阻抗计算。仿真结果如表2和表3所示。

由表2、表3可以看出，仿真系统在正态扰动下，方法4的计算结果较其他方法误差最小。4种方法对3次、5次、7次、9次、11次、13次谐波的测量值如图5和图6所示。

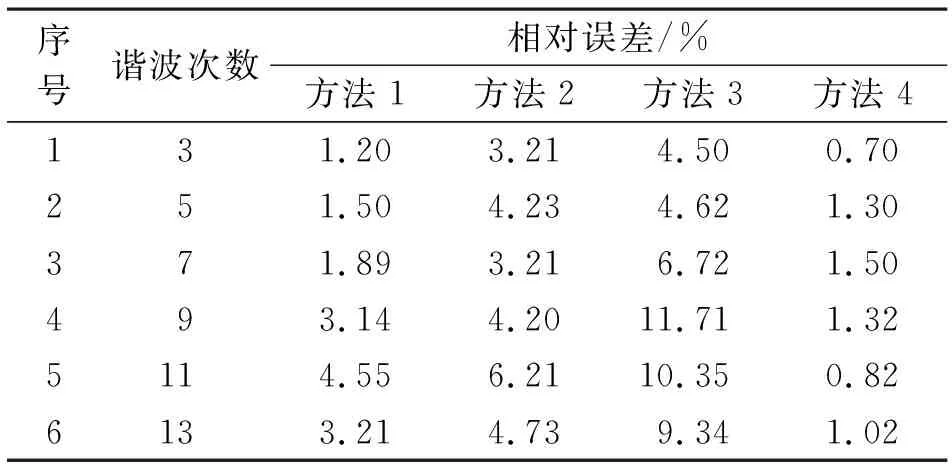
表2 系统阻抗幅值误差

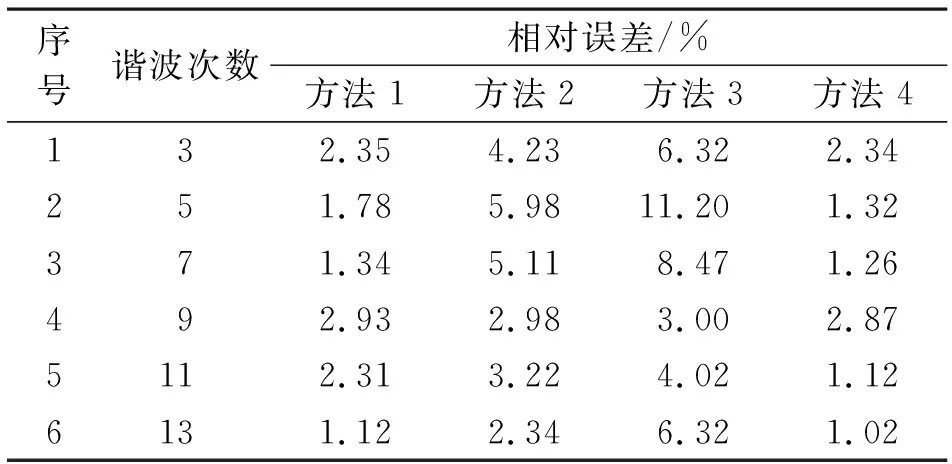
表3 系统阻抗相角误差

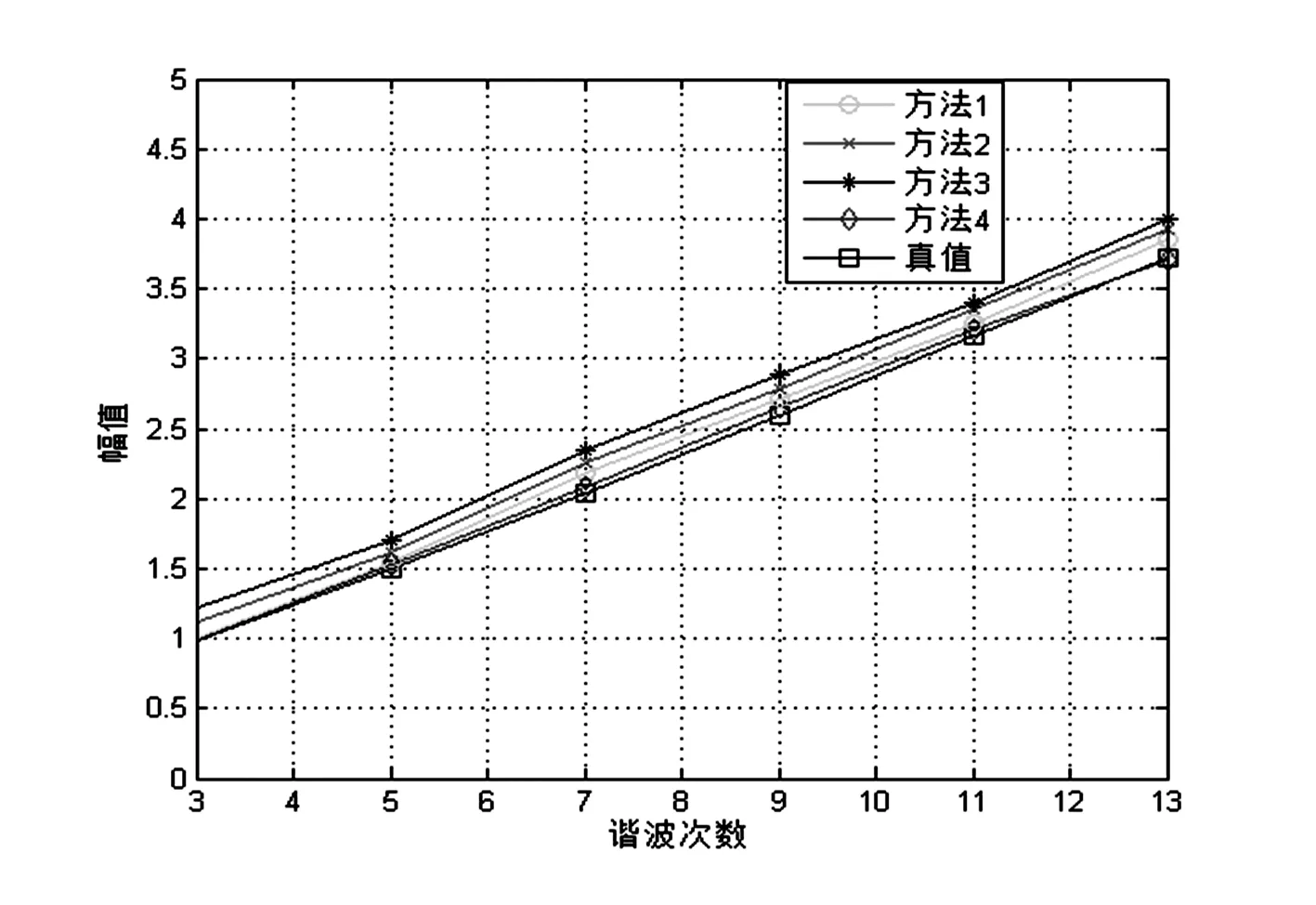
图5 正态谐波背景下不同方法计算的阻抗幅值

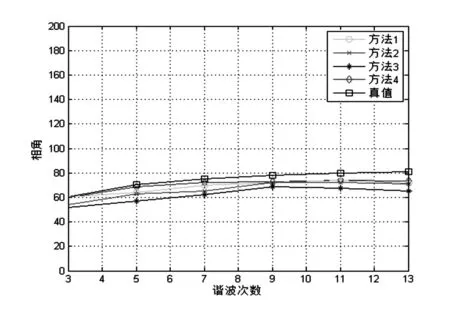
图6 正态谐波背景下不同方法计算的阻抗相位

2.2.2 非正态背景谐波

将负荷侧扰动设置为非正弦扰动，与2.2.1节做相同的建模和计算，结果见表4、表5、图7、图8。

表4 系统阻抗幅值误差

表5 系统阻抗相角误差

图7 非正态谐波背景下不同方法计算的阻抗幅值

图8 非正态谐波背景下不同方法计算的阻抗相位

由表4和表5 的仿真结果可以发现，在非正态随机扰动之下，所提的方法4对典型谐波的测量计算仍然保持着较高的准确率。并且，对比表2至表5，可以发现方法4在正态扰动和非正态扰动下计算结果十分接近，表明该方法可以有效地抑制背景谐波的干扰，从而使得计算效果更加准确稳定。

3 结 语

系统侧谐波阻抗的计算是评估用户谐波发射水平以及研究谐波在系统中各类特性的基础。区别于对谐波污染等效分析模型中数据处理的算法研究，根据大量实际工程经验，以及在用户侧变电站故障录波装置中获取的波形与数据，提出了系统侧谐波阻抗计算的新思路，即聚焦于用户侧发生故障时的前期阶段，PCC处的谐波波动量只与用户侧谐波波动量有关的特点。在该情况下，可以认为系统侧谐波波动量不影响PCC处的谐波波动伏安特性比。因此，可据此快速计算系统侧谐波阻抗。

通过仿真分析以及和其他计算系统侧谐波阻抗方法的对比，可以看出所提方法的计算结果最接近真值，受到用户侧谐波发射水平的影响也最小。此外，所提的基于故障分量的系统侧谐波阻抗计算方法十分简便，可以通过用户侧变电站的故障录波装置获取数据与波形，是工程研究人员非常易于掌握的计算方法。所做研究工作对更科学地评估用户谐波发射水平以及划分谐波污染责任有一定指导作用。