车载捷联惯导双里程计组合导航方法研究

郭楠楠，申亮亮，邵会兵，苑艳华

(北京控制与电子技术研究所，北京 100038)

0 引言

导航是指将运动载体从甲地引导到乙地的技术。为了完成引导任务，首要问题是确定载体的即时位置；为了实现经济和快速导航，还需要测定载体的速度和姿态等运动参数，进而引导运载体迅速精确地驶向既定目标。所以导航的基本任务是确定载体的姿态、速度和位置等导航参数。

在军事领域中，现代地面战争要求载车能够在广阔的作战地域内灵活机动，并为武器发射提供精确的地理坐标和水平北向基准，做到停车就打或者边走边打，提升车载武器平台的机动性，提高生存能力和快速反应能力，保证精确打击精度，提升作战效能。随着卫星导航系统的逐步完善，由于卫星导航定位精度高且长期稳定性好，惯性/卫星组合导航技术很容易满足车载导航系统动态定位和定向的要求。但是，卫星导航需要接收外部无线电信号，容易受到干扰甚至欺骗，在敏感地区和时间内载车不能完全依赖车载捷联惯导系统和卫星进行组合导航[2]，各国的军用车载导航系统都对卫星导航采用了用而不靠的原则。因此，研制成本低、精度高、准备时间短和自主性强的车载组合导航系统具有重要的军事和现实意义。

作为军事用途的车辆，自主性和隐蔽性至关重要，在系统构成上应优先采用“不接收任何信息，也不向外辐射任何信息”的导航子系统。车载捷联惯导和车载里程计都具有不依赖外部设备和不受外部信号干扰的特点，所以该组合是一种理想的车载导航方案。在目前公开的文献中，车载捷联惯导和车载里程计组合导航时，将里程计安装在车底盘左侧或右侧位置，该方法虽然是自主式组合导航的有效手段，但由于安装误差的存在，里程计信息未能真实反映车体中心的实际运行状态，且里程计量测信息误差会引入未知的导航误差，从而影响系统组合导航的定位精度。

本文针对军事车辆对自主导航的需求背景和高精度精确打击的要求，系统地提出了一种由车载捷联惯导和车载双里程计构成的高精度全自主车载组合导航方案。该方案分别在车底盘左侧和右侧位置各安装一个里程计，将双里程计信息作为量测量设计组合导航融合算法，并采用序贯处理的方式进行Kalman滤波组合导航以减少计算量；且在导航过程中对双里程计输出信息进行χ2检测，有效剔除了车体作大转弯运行或有外部干扰时引起的里程计信息异常，确保了里程计信息的有效性，且相对于单里程计具有容错功能，从而保证了系统的定位和定向精度。

1 组合导航系统原理

在算法设计上，一方面惯性测量单元(Inertial Measurement Unit，IMU)信息分别与两路里程计信息组合解算出载体的速度、位置和姿态信息；另一方面，两路里程计量测信息考虑安装误差变化后，通过构造速度/位置量测模块，形成速度/位置量测Kalman滤波导航系统，再将两路量测信息形成故障检测系统，通过χ2检测方案对系统量测值的可信度，即双里程计的输出进行对比判断，判别应使用哪个里程计进行导航计算。在2个里程计均有效的情况下，采用序贯处理的方式使用双里程计的量测值进行Kalman滤波处理。每隔一段时间对惯性导航系统的速度误差、姿态误差、位置误差、加速度计零偏、陀螺漂移等误差和里程计误差参数进行闭环修正，实时输出修正后的位置、速度和姿态信息，形成高精度的组合导航系统。具体原理如图1所示。

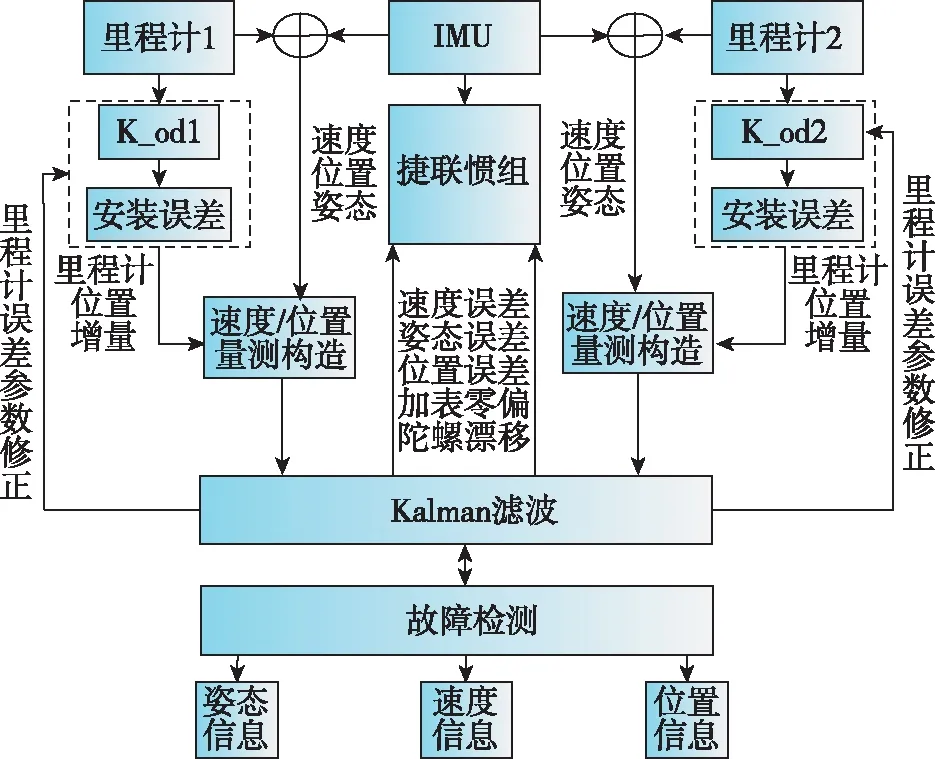
图1 组合导航系统原理图Fig.1 Schematic diagram of integrated navigation system

2 组合导航融合算法模型

2.1 里程计输出模型

里程计通常采用脉冲数方式输出采样时间间隔内的里程增量。定义里程计坐标系为m系，Y轴沿车体纵轴指向正前方，x轴沿车体横轴指向右侧，z轴垂直于X轴和Y轴并构成右手直角坐标系。里程计采样时间间隔内输出的脉冲数Ni在m系的投影写成矢量形式为

(1)

设惯导系统确定的载体坐标系为b系，则里程计输出的位置增量在b系的投影为

(2)

(3)

(4)

式中，ωd为随机噪声干扰，忽略二阶小量，里程计输出的b系位置增量可以写成

(5)

其中

2.2 INS /OD状态方程和量测方程

状态量为27维，包含SINS的15维和6维里程计1误差、6维里程计2误差(刻度因子误差、俯仰安装误差、航向安装误差以及杆臂误差dL)，双里程计刻度系数误差和安装误差均视为随机常数，状态方程如下

dLk1,dKd2,dαθ2,dαψ2,dLk2]T

(6)

(8)

(9)

(10)

(11)

(12)

(13)

式中

M2=

M4=(vn×)(M1+M′)

M6=

若采用速度量测方式，构造量测方程如下

(14)

(15)

考虑到平台失准角φn，有

忽略二阶小量

(16)

故由此可得速度量测为

(17)

Zv=Hv·X+VD

(18)

Hv=

(19)

式中

同理可得另一路里程计量测方程。

2.3 Kalman滤波

2.3.1 系统离散化

Kalman滤波方程适合离散型的系统方程和量测方程式，将上述系统方程和量测方程式离散化为如下形式

(20)

连续状态矩阵F(t)的计算周期Ts可大于惯性导航解算周期Δt，本方案中取值为0.01s，即滤波器的时间更新周期为0.01s。对计算出的矩阵F(t)进行离散化，即可得离散状态转移矩阵Φk/k-1为

Φk/k-1=eFTs≈I+FkTs

(21)

其中，Fk=F(tk)。

系统噪声的离散化如下

(22)

2.3.2 故障检测

组合导航系统的故障检测是组合导航系统的可靠性保障，可以分为单机级故障检测和系统级故障检测。单机级的故障检测是在传感器出现明显异常时发出故障信息，从而不去参与系统运算，已经在各传感器中实现了故障实时监测；系统级的故障检测方法，主要是避免因故障子系统对滤波器的影响，从而导致滤波发散的问题。在滤波中配备实时的故障检测及隔离算法，一旦检测到故障就必须对故障进行隔离。最后通过系统信息重构，快速实现剩余子系统重组，使整体系统不致因故障而失效，保证组合导航系统在任务期间的战备完好性和可靠性。

在容错组合导航系统中，必须实时地确定各量测信息的有效性，以便决定是否进行组合。这样做的原因是防止任意导航子系统的故障污染到其他状态，提高组合系统输出的导航信息的可靠性。

针对组合导航系统的特点，采用一种残差χ2检验法来确定系统量测信息的有效性。该方法并不确定造成故障的具体原因，而仅仅是实时地确定一组量测的有效性，因此十分适用于系统级的故障检测及隔离。

Kalman滤波器在量测更新时的残差为

(23)

当无故障发生时，Kalman滤波器的残差rk是零均值高斯白噪声，而其方差为

(24)

可以得到故障检测函数为

(25)

其中，λk是服从自由度为m的χ2分布，即λk～χ2(m)，其中m为量测维数，则故障判定准则为：若λk>TD则判断为有故障；若λk

预先设定的判断门限TD可由误警率查χ2分布表得到。当检测发现某一时刻任意一个里程计信息故障，则认为该里程计数据异常，对当次量测作丢弃处理，只进行状态更新而不进行量测更新和滤波修正。

2.3.3序贯处理

序贯处理将量测更新中对量测量的集中处理分散为对各组的顺序处理，有效降低了计算量，且能很好地进行单个传感器的故障识别，将双里程计的量测方程写成如下形式

(26)

序贯处理量测更新过程如图2所示。

图2 序贯处理流程示意图Fig.2 Flow diagram of sequential processing

3 试验验证

采用激光陀螺捷联惯导系统进行车载试验验证，惯导系统中陀螺精度为0.01(°)/h、加速度计精度为5×10-5g，系统自带定位精度为2m(CEP)的GPS接收机，可作为位置考核基准。2个里程计在组合导航前经过预先标定，得到里程仪1的标度因数和安装偏差角为KD1=0.036087、αθ1=0.5687919、αψ1=0.88269，里程仪2的标度因数和安装偏差角为KD2=0.036337、αθ2=0.592625、αψ2=0.923592。

车载试验持续时间约6600s，跑车路径如图3所示，图4所示为融合算法和单里程计组合导航算法的定位误差对比结果图，图5～图11所示分别为融合算法的位置估计误差曲线、陀螺漂移估计误差曲线、加速度计零偏估计误差曲线、里程计安装角度和标度因数估计误差曲线、里程计杆臂估计误差曲线、组合导航姿态估计曲线和里程计数据故障检测值。图4和图5的误差为与GPS比较的结果，其中有些时刻因GPS数据无效而导致误差较大。由图4可以看出，采用融合算法后定位误差整体减小到20m以内，最大处减小6m。

图3 车载试验行车路径曲线Fig.3 Vehicle test route curve

图4 定位误差对比结果Fig.4 Positioning error comparison results

图5 位置估计误差曲线Fig.5 Position estimation error curve

图6 陀螺漂移估计误差曲线Fig.6 Error curve of gyro drift estimation

图7 加速度计零偏估计误差曲线Fig.7 Error curve of accelerometer bias estimation

(a) 里程计1安装角度和标度因数估计误差曲线

(b) 里程计2安装角度和标度因数估计误差曲线

(a) 里程计1杆臂估计误差曲线

(b) 里程计2杆臂估计误差曲线

图10 组合导航姿态估计曲线Fig.10 Integrated navigation attitude estimation curve

(a) 里程计1数据故障检测值

(b) 里程计2数据故障检测值图11 里程计1/2数据故障检测值Fig.11 Data fault detection value of odometer 1/2

在本次实验中，在4000～4600s内给里程计2数据加入故障(故障值大小：50)，再次验证算法的有效性，故障卡方检测值和融合结果如图12所示。

图12 里程计1数据故障检测值Fig.12 Data fault detection value of odometer 1

从图13可以看出，虽然在4000～4600s内里程计2异常，卡方检测能够及时检测出故障，且在发现故障后，不进行里程计2的量测更新，只利用里程计1的信息进行量测更新，使定位结果能达到最优；数据正常后，卡方检测能同时识别出，故障能立即恢复。

图13 里程计2加入异常数据故障检测值Fig.13 Chi-square test results of odometer 2 with abnormal data fault detection value

4 结论

本文将单位时间内惯导解算位置增量和双里程计航位推算位置增量之差作为量测值，设计了27维的捷联惯导/双里程仪组合导航滤波算法。采用序贯处理的Kalman滤波融合算法有效减少了计算量，且双里程计具有容错功能，可提高系统的稳定性和可靠性，工程可实现性强。车载试验结果表明，该组合算法正确有效，定位结果能得到最优融合，可以达到理想的定位和定向精度。