利用改正数信息的北斗三号实时精密单点定位及性能分析

王 乐，解世超，王浩浩，岳 帆，黄观文

(长安大学地质工程与测绘学院，西安 710054)

0 引言

2020年6月23日，北斗三号最后一颗全球组网卫星发射成功，标志着北斗三号星座部署完成。北斗三号星座包括三种类型轨道卫星，分别为3颗地球静止轨道(Geostationary Earth Orbit, GEO)卫星、3颗倾斜地球同步轨道(Inclined Geo Synchronous Orbit, IGSO)卫星和24颗中圆地球轨道(Medium Earth Orbit, MEO)卫星。目前，北斗三号部分卫星尚未对外提供服务或服务产品精度低。同时，GEO卫星和IGSO卫星由于观测数据数量和质量等原因，服务效果有待提高。

随着北斗系统实时应用领域的不断拓展和深入，用户对实时定位精度的要求越来越高。目前，能够提供用于单点定位的实时产品主要包括广播星历[1]、超快速星历[2]和实时改正数信息[3]。很多学者对此进行了大量研究。孟祥广等研究表明，北斗二号广播星历轨道精度基本优于2m，钟差精度约为10ns[4]。王海春等通过试验获得的北斗三号卫星广播星历轨道三维方向精度优于1m，钟差精度优于3.5ns[5]。可见，北斗广播星历轨道和钟差精度相对较低。黄观文等研究表明，超快速星历预报6h钟差精度约为1ns，12h优于3ns[6]。杨宇飞等分析得到，北斗二号超快速钟差预报24h精度约为7～9ns[7]。可见，超快速产品预报钟差精度较低。张龙平等计算的北斗二号IGSO和MEO卫星实时轨道精度优于30cm[8]。王乐等研究了北斗三号卫星实时轨道和钟差解算方法，获取的北斗三号MEO卫星实时轨道和钟差优于30cm和0.5ns[9]。

在利用实时改正数信息进行实时精密单点定位方面，夏凤雨等利用改正数修正广播星历后的实时精密单点定位各方向精度均优于20cm[10]。王乐等利用播发的全球定位系统(Global Positioning System，GPS)实时改正信息计算的实时定位平面和高程精度分别优于10cm和20cm，收敛时间约为40min[11]。刘行波等基于北斗二号实时轨道和钟差，利用双频信号获得了分米级动态定位精度，收敛时长约为1h[12]。但是，目前针对北斗三号实时精密单点定位性能分析的研究较少。

本文首先利用全球分布的国际GNSS监测评估系统(international GNSS Monitoring and Assessment System, iGMAS)和多模GNSS实验网络(the Multi-GNSS Experiment，MGEX)监测站解算了北斗三号卫星实时精密轨道和钟差，并获取了实时改正数。然后利用改正数和广播星历分别进行了双频静态、双频动态、单频静态、单频动态仿实时定位，并分析了其定位精度和收敛时长等性能。

1 利用改正数信息的实时精密单点定位方法

利用实时改正数进行实时精密单点定位，在获取测站实时观测数据和广播星历的同时，还需获取卫星实时精密轨道和钟差改正数，并进行实时轨道和钟差改正。在进行单频实时精密单点定位时，还可能需要高精度的实时电离层参数信息。

实时改正数信息通过星历数据期号(Issue of Data Ephemeris, IODE)参数与广播星历进行匹配，进而进行参数修正。对于GPS、GLONASS和GALILEO系统，IODE可从广播星历直接获取，但是北斗三号广播星历中相应位置参数暂不可用，因此本文IODE通过广播星历中周内秒参数计算获取，具体方法参考文献[13]，实时轨道和钟差解算参考文献[9]。

1.1 实时轨道改正

实时轨道改正数信息中包含轨道坐标系下切向、法向和径向的卫星位置和速度改正数[14]。通过与广播星历进行匹配并修正后，可获取高精度卫星轨道。

改正数播发具有一定时间间隔，通过参考时刻轨道改正数计算当前时刻实时轨道[13]，主要可概括为以下步骤：

1)根据轨道坐标系下参考时刻卫星位置和速度改正数，计算当前时刻卫星位置改正数；

2)根据计算的当前时刻广播星历卫星位置和速度，计算轨道坐标系到地心空间直角坐标系的旋转矩阵；

3)计算当前时刻地心空间直角坐标系下卫星位置改正数，并获取卫星精确位置。

1.2 实时钟差改正

设钟差改正数在参考时刻t0时的多项式系数为C0、C1、C2，则当前时刻t时以距离形式表示的钟差改正值δC为[15]

δC=C0+C1(t-t0)+C2(t-t0)2

(1)

经改正后的卫星精密钟差δt为

(2)

式中，C表示真空中光的传播速度;δts表示广播星历t时刻的卫星钟差。

1.3 实时精密单点定位

利用实时获取的轨道、钟差改正数和广播星历，按上述1.1和1.2节中的方法计算当前时刻的精密轨道和钟差，对观测数据进行预处理后，采用滤波方法进行实时精密单点定位[16]。具体数据处理流程如图1所示，数据处理策略如表1所示。

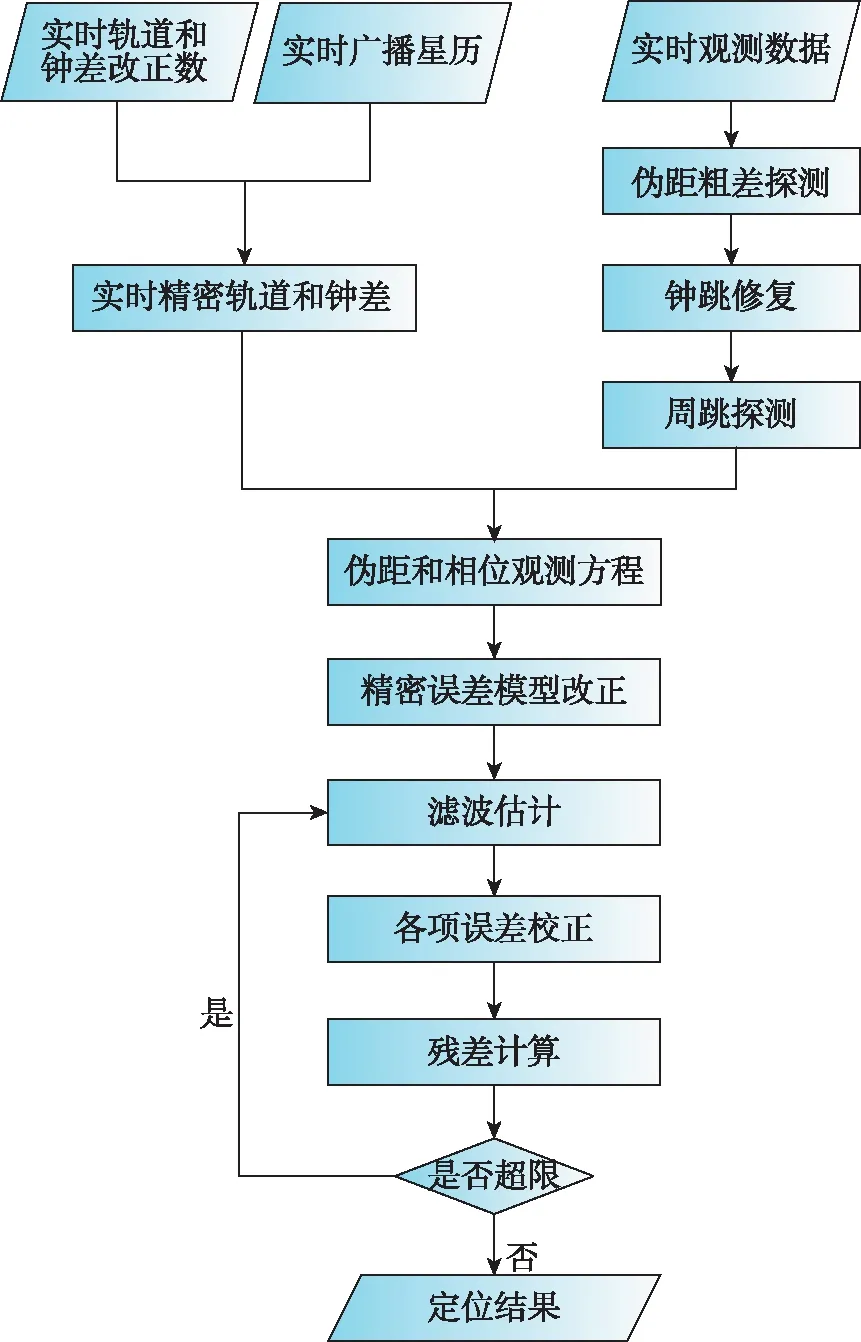
图1 实时精密单点定位数据处理流程Fig.1 Data processing flowchart of RT PPP

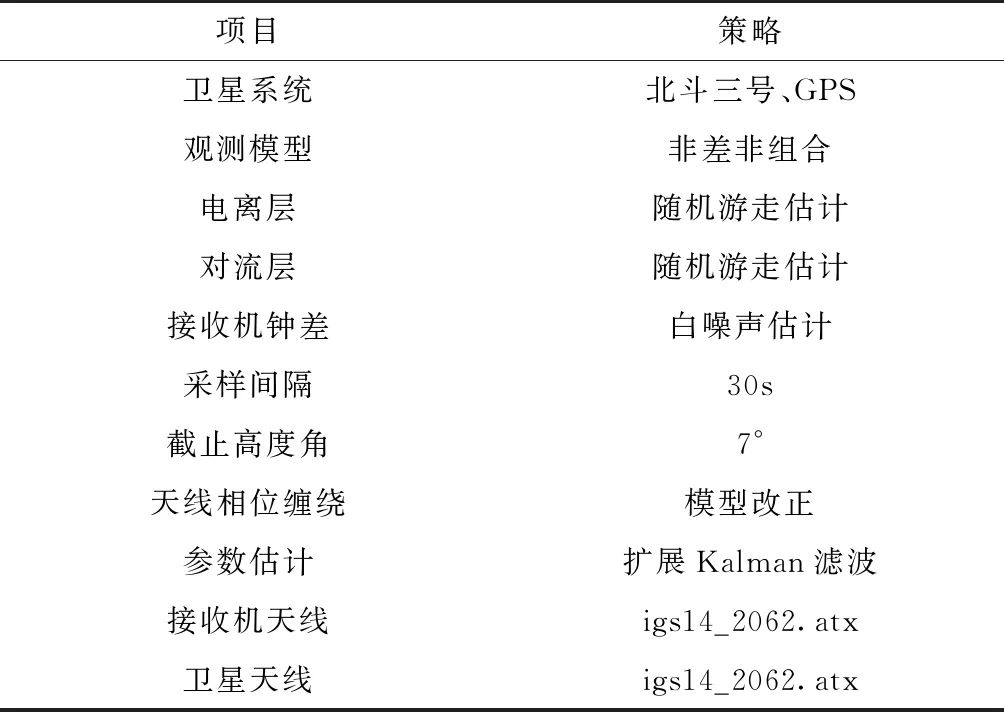
表1 实时精密单点定位数据处理策略

2 实时改正数精度分析

利用北斗三号和GPS双系统观测数据实时解算了2020年6月23日(年积日175)的实时轨道和钟差产品。

2.1 实时轨道精度分析

选取全球分布的可接收北斗三号B1I/B3I频点双频信号的13个iGMAS和45个MGEX监测站的观测数据，测站分布如图2所示。图2中，蓝色圆点表示iGMAS监测站，橙色圆点表示MGEX监测站。北斗三号目前仅有部分MEO卫星可提供稳定服务，且缺乏与国际GNSS服务组织(International GNSS Service, IGS)14框架一致的卫星以及接收机相位中心等相关改正，单北斗解算效果相对较差，加入GPS观测数据与北斗三号同时处理可在保障解算效率的同时，将轨道与钟差产品同IGS14框架对齐，并提高测站坐标和对流层延迟改正等公共参数的解算精度。为同时保证解算效率和精度，仅选取部分北斗三号MEO和GPS卫星参与解算。选取72h实测数据进行高精度精密定轨，并通过拟合外推方法获取高精度预报轨道。每隔1h解算一次，选取预报部分2～3h弧段作为实时轨道，并匹配到最近的实时广播星历，生成实时轨道改正数。

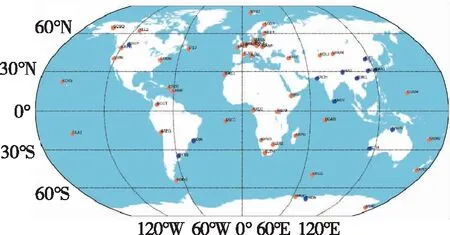
图2 实时精密定轨测站分布图Fig.2 Stations distribution of real-time precise orbit determination

除了传统的动力学法精密定轨模型和策略，本文实时精密轨道及改正数解算策略和关键模型还包括：太阳光压模型选取ECOM 5参数模型；测站坐标从IGS发布的igs20P2086.snx文件中提取或通过事后精密单点定位解算，并对其进行紧约束；北斗三号MEO卫星天线相位中心改正采用北斗官方发布的地面标定值，其他接收机天线和卫星天线相位中心改正均来自IGS发布的igs14_2062.atx文件。

选取武汉大学iGMAS分析中心发布的精密快速轨道产品为基准，评定北斗三号MEO卫星实时轨道一维精度。统计其一维均方根(Root Mean Square, RMS)如图3所示。

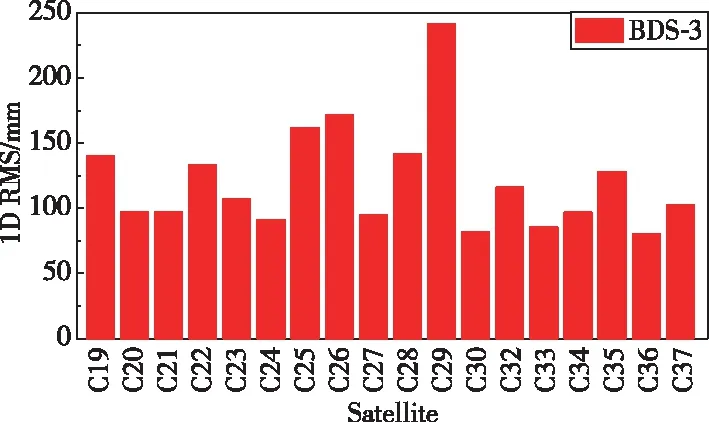
图3 北斗三号MEO卫星实时轨道精度统计Fig.3 Real-time precise orbit accuracy statistics of BDS-3 MEO satellites

从图3可以看出，目前解算的北斗三号所有MEO卫星实时轨道精度均优于25cm，大部分卫星优于15cm，均值约为12cm。除C29卫星精度稍差，其他卫星精度基本一致，完全满足实时精密定轨的精度要求。

2.2 实时钟差精度分析

选取全球分布的10个iGMAS和35个MGEX监测站，由于北斗三号单系统实时钟差估计存在与上述单系统精密轨道解算相同的问题，故采用北斗三号和GPS双系统联合解算。采用采样间隔为1s的BDS B1I/B3I和GPS L1/L2P实时高频观测信号，基于2.1节解算的实时精密轨道进行实时卫星钟差估计。测站分布如图4所示。

在进行实时卫星钟差估计时，采用无电离层组合观测量，并根据高度角定权、模型改正相位缠绕和相对论效应等，固定卫星轨道和测站坐标。将每个测站的天顶对流层延迟作为分段常数进行估计，每个连续弧段的模糊度作为常数进行估计，卫星和接收机钟差作为白噪声进行估计。

选取武汉大学iGMAS分析中心发布的精密快速钟差产品为基准，进行二次差比较[17]，评定北斗三号MEO卫星实时钟差内符合精度。统计其标准偏差(Standard Deviation, STD)如图5所示。

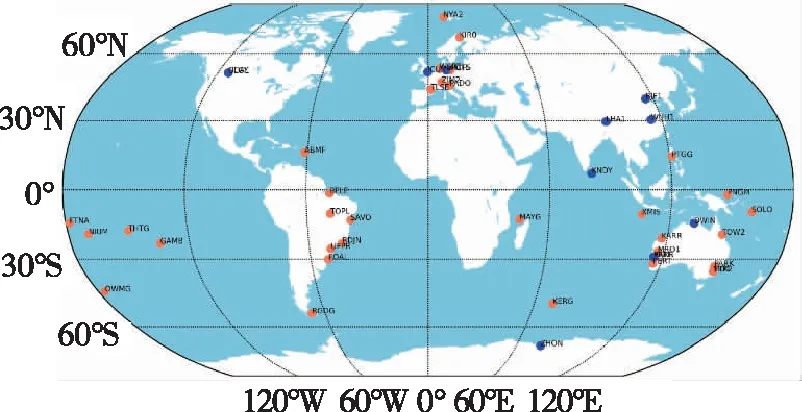
图4 实时精密卫星钟差估计测站分布图Fig.4 Stations distribution of real-time precise clock offset estimation

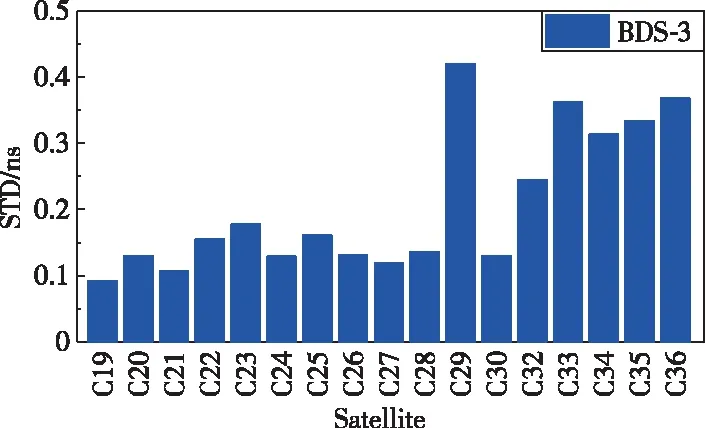
图5 北斗三号MEO卫星实时钟差内符合精度统计Fig.5 Real-time precise clock offset accuracy statistics of BDS-3 MEO satellites

从图5可以看出，北斗三号MEO卫星实时钟差STD值大部分优于0.35ns，平均STD值约为0.2ns。其中，C29卫星受实时轨道精度影响，解算精度偏差；C32～C36卫星实时钟差精度明显低于其他卫星，原因为上述卫星的实时观测数据量相对较少。随着北斗三号地面监测站的建设和测站接收机的升级，这一现象将得到改善或消失。

3 实时精密单点定位精度分析

选取8个MGEX测站2020年第175天4～14时共10h的数据，利用上文解算的卫星实时轨道和钟差改正数进行北斗三号/GPS双系统仿实时精密单点定位解算，测站信息如表2所示。

本文分别利用上述测站观测数据进行了双频静态、双频仿动态、单频静态和单频仿动态仿实时精密单点定位。然后以IGS公布的周解坐标为基准，计算E、N、U这3个方向的偏差。当E、N、U方向连续10min位置偏差小于30cm时，认为收敛。

由于篇幅原因，本文仅随机选取了yar3测站展示定位结果的时间序列图。

3.1 双频静态定位

各测站双频静态实时精密单点定位收敛时间及精度统计结果如表3所示。yar3测站双频静态定位时间序列图如图6所示。

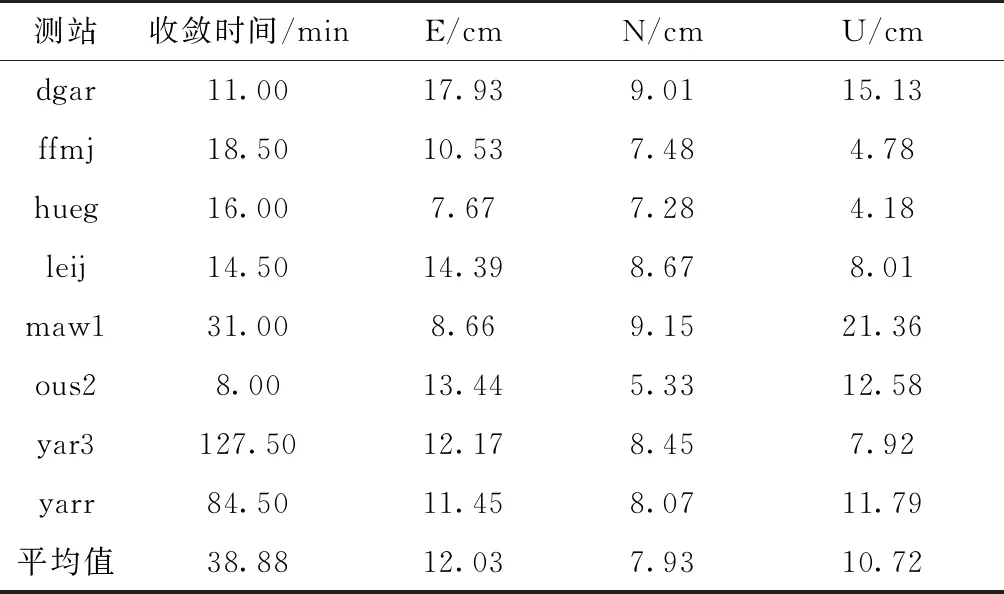
表3 双频静态定位结果统计

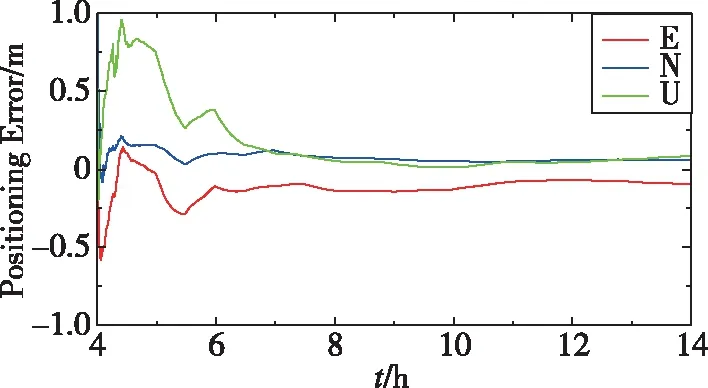
图6 yar3测站双频静态定位时间序列图Fig.6 Dual-frequency static positioning time series of yar3 station

由表3可知，双频静态实时精密单点定位收敛后，E方向精度基本优于15cm，N方向精度优于10cm，U方向精度各站差别相对大，约在5～21cm之间，平均约为11cm。各测站的收敛时间差别较大，平均约为40min。初步分析，不同测站收敛时间存在差异的原因是各个测站的数据质量不同，并且初始时卫星的空间几何分布也有所不同。不同测站定位精度存在差异的原因可能是各个测站的数据质量不同，并且各站数据解算过程中对轨道和钟差产品的误差影响的抑制效果也存在差别。从图6可以看出，双频静态实时精密单点定位收敛后结果稳定。

3.2 双频动态定位

各测站双频动态定位收敛时间及精度统计结果如表4所示。yar3测站双频动态定位时间序列图如图7所示。

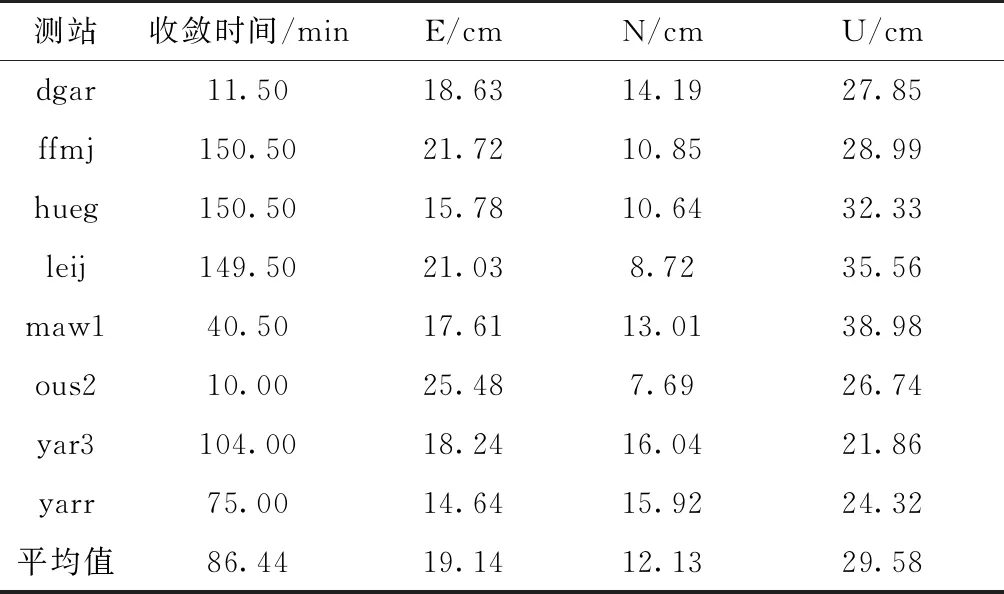
表4 双频动态定位结果统计

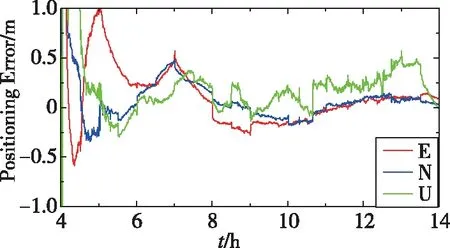
图7 yar3测站双频动态定位时间序列图Fig.7 Dual-frequency kinematic positioning time series of yar3 station

由表4可知，双频动态定位E方向平均精度优于20cm，N方向优于15cm，U方向优于30cm。各测站平均收敛时间约为85min。从图7可以看出，双频动态定位结果收敛后仍有亚分米级、甚至分米级波动。

3.3 单频静态定位

各测站单频静态定位结果如表5所示。yar3单频静态定位时间序列图如图8所示。

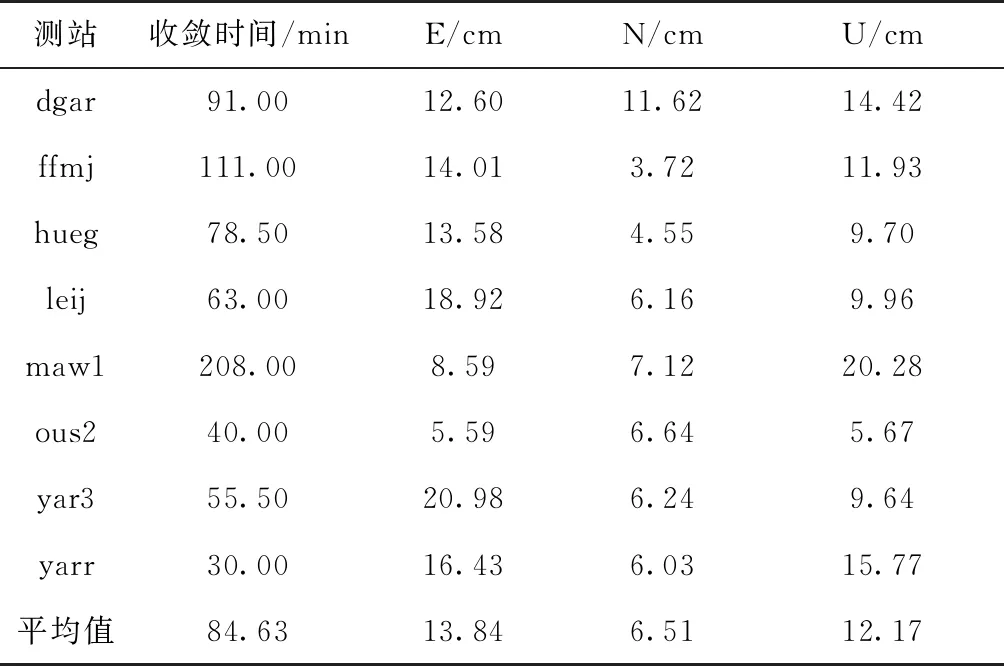
表5 单频静态定位结果统计

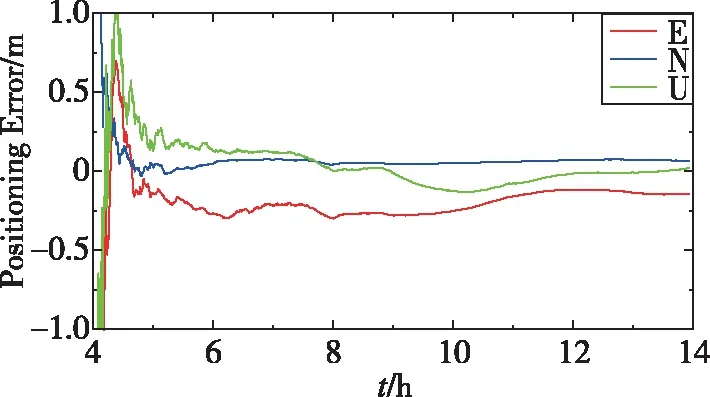
图8 yar3测站单频静态定位时间序列图Fig.8 Single-frequency static positioning time series of yar3 station

由表5和图8可知，单频静态定位N方向平均精度优于10cm，E和U方向优于15cm，平均收敛时间约为85min，收敛后定位结果稳定。

3.4 单频动态定位

各测站单频动态定位结果如表6所示。yar3单频动态定位时间序列图如图9所示。

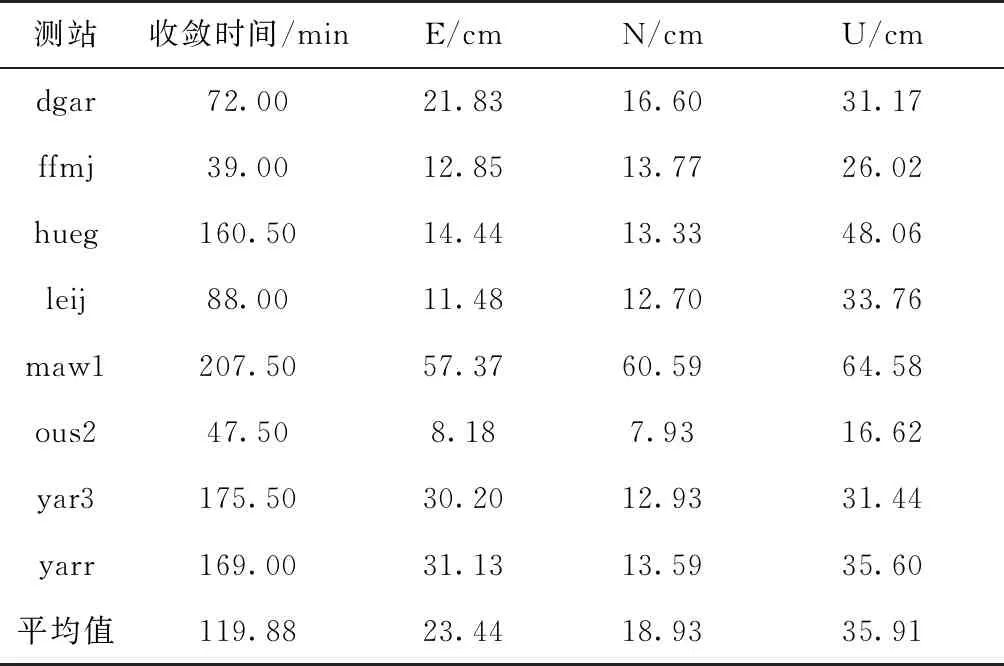
表6 单频动态定位结果统计

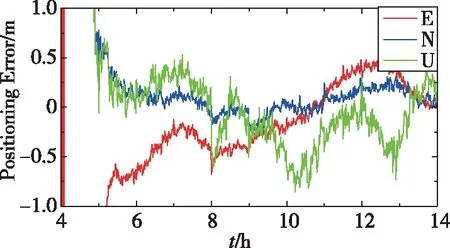
图9 yar3测站单频动态定位时间序列图Fig.9 Single-frequency kinematic positioning time series of yar3 station

由表6和图9可知，单频动态定位E、N、U方向平均精度分别约为25cm、20cm和35cm，平均收敛时间约为120min，收敛后结果仍有较大波动。

4 结论

本文针对利用实时改正数信息的北斗三号实时精密单点定位进行了系统的研究，完整计算了北斗三号MEO卫星实时轨道和钟差改正数，以及双频/单频静态/动态实时精密单点定位，并对其进行了评估分析，研究结果表明：

1)除个别卫星，北斗三号MEO卫星实时精密轨道平均精度基本优于15cm，均值约为12cm；实时精密钟差平均精度基本优于0.35ns，均值约为0.2ns。解算的实时改正数信息满足实时精密单点定位需求。

2)利用改正数信息进行的实时精密单点定位，单双频静态定位E、N、U方向精度分别优于15cm、10cm、15cm;双频动态定位精度分别优于20cm、15cm、30cm;单频动态定位精度分别约为25cm、20cm和35cm。静态定位精度高于动态定位，双频定位精度高于单频定位，均达到分米级。

3)双频静态定位收敛时间约为40min，单频静态和双频动态定位收敛时间均约为85min，单频动态定位收敛时间约为120min。静态定位收敛时间短于动态定位，双频定位收敛时间短于单频定位。静态定位收敛后结果稳定，动态定位收敛后结果仍存在波动。

4)随着正式对外提供高精度服务的北斗三号卫星数量增多和可接收北斗三号观测信号的地面监测站的建设或升级，北斗三号实时精密单点定位等服务性能将进一步提升。