基于局部几何特征的稠密点云配准方法

朱一帆，裴 凌，吴 奇，夏宋鹏程，李 涛，陈 雷,2，郁文贤

(1.上海交通大学上海市北斗导航与位置服务重点实验室，上海 200240； 2. 北京跟踪与通信技术研究所，北京 100094)

0 引言

近年来，随着传感器技术的进步，三维点云数据在精度和稠密度方面获得了大幅提升[1]，三维点云数据作为重要的空间结构数据，被广泛地应用于自主导航和三维场景重建等。对稀疏的三维激光点云配准问题已经进行了较为深入的研究，稠密的三维点云的配准问题成为了研究热点。

迭代最邻近点 (Iterative Closest Point，ICP)算法是解决点云配准问题的核心算法。该算法采用点点(点面)距离寻找邻近点,再通过最小二乘法求取点云间的旋转和平移矩阵，以达到点云配准的目的,其实质是一种迭代收敛的算法[2]。随着三维点云数据稠密程度的提高，现有的基于ICP算法的三维点云配准方法由于计算量大、 依赖初始位置设定等因素，配准成功率不高。

在视觉同时定位与建图(Visual Simultaneous Localization and Mapping，VSLAM)中[3-4]，通常对点云数据进行局部特征抽取，再基于特征进行配准，可以大幅减少点云数量，提高配准的鲁棒性。由于三维点云的无序性和传感器的噪声，点云局部特征的描述工作相对图像特征要困难很多，这也造成了现有的点云描述子的鲁棒性不足，在进行点云配准的过程中位姿恢复精度较低[5]。随着深度学习技术的兴起，基于数据驱动的模型被用于三维点云局部特征的描述上，并且表现非常出色。实验证明，基于数据驱动的模型对点云局部的几何结构能够进行有效的描述，并在特征空间上能够很好地进行聚类，效果优于现有的手动设计的描述子[6]。

基于上述原因，本文提出了一种基于点云局部几何特征的稠密点云配准方法。该方法借鉴VSLAM算法中图像匹配的思路[7]，对点云进行局部特征抽取和描述，然后进行位姿估算。在局部特征提取方面，使用深度卷积网络对特征进行描述，以减少三维点云数据的噪声、低分辨率和不完备性等带来的影响。该方法的优势在于精度高、计算量低，且能够匹配位姿差异大的点云。实验结果验证了该方法的有效性、实时性和鲁棒性。

1 算法设计

点云的配准工作主要可以描述为：求解两帧三维点云的旋转平移矩阵(6个自由度)，使两帧点云能够对齐到同一个坐标系上。本文提出的点云配准方法技术路线如图1所示。对于给定的两帧点云，分别计算其特征点和特征描述之后，通过随机采样一致(Random Sample Consensus，RANSAC)算法对两帧三维点云的旋转平移矩阵进行鲁棒的估计。

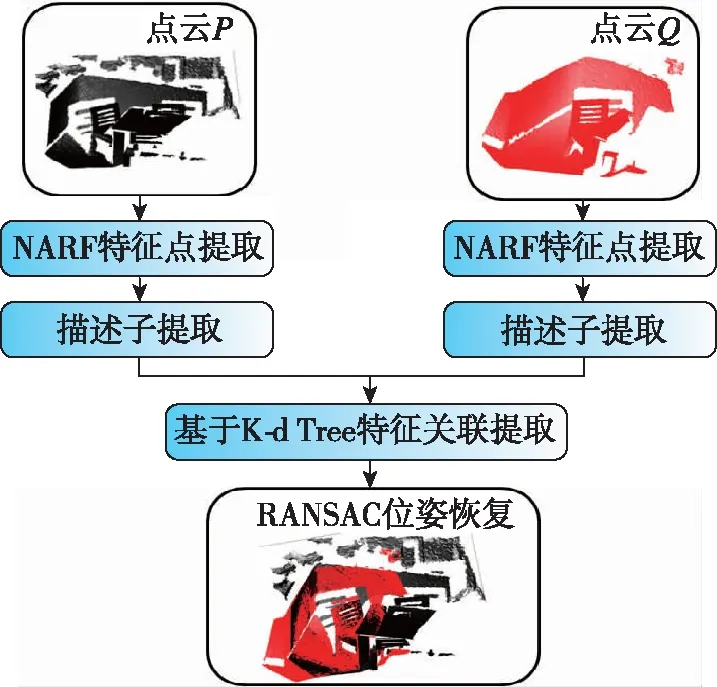
图1 3D点云配准方法算法流程Fig.1 3D point cloud registration algorithm flow

1.1 特征点检测

三维点云(P={p1,p2,…，pn})可以被描述为一些离散三维点(pi=[xi,yi,zi]T,xi,yi,zi∈R)的集合。其中特征点检测算法的目的是寻找该集合的一个子集(K⊆P)，使其能够尽可能地代表原来集合的信息。对于点云配准这一具体应用，所选取的关键点要满足以下要求：1)特征点的提取算法要求效率高；2)在不同的视点下都能提取到大部分相同的特征点；3)提取出的特征点应位于表面稳定的区域，以保证稳定的特征提取。

法线对齐的径向特征(Normal Aligned Radial Feature，NARF)是一种3D特征点检测和描述算法[8]。其特征点选取算法能够很好地满足上述要求，因此，在本文的点云配准方法中选用NARF特征点。首先，将目标点云转化为距离图像便于快速检索以保证要求1)；然后，对于每一个三维点pi，选择其在距离图像上的一个方形窗(窗宽为：s)内的邻域点，并计算其与pi的三维距离；之后按照式(1)计算三维点pi的分数

(1)

其中，di是pi在距离图像上与其上下左右4个方向上的邻接像素点的平均三维距离；dM是方形窗内一系列点中距离pi第M远的点与pi的三维距离，其中M=(0.5(s+1))2。当分数高于一定阈值时，认为三维点pi满足要求2)，并将其列入候选关键点列表。对于候选关键点列表中的pi，在点云中找到其在半径σ中的所有领域点：n0,…,nk。评分函数I(p)被用以评估三维点pi对要求3)的满足情况，定义为

I(p)=I1(p)I2(p)

(2)

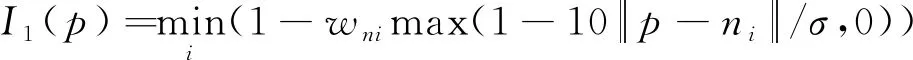
其中，α是pi和其所有领域点中不是边界点的主方向；wn是一个权重，对于边缘点取值为1，非边缘点取值为1-(1-λ)3，λ代表非边缘点的曲率大小。当候选关键点列表中的某个pi的分数I(pi)大于一定阈值时，该点被选为特征点。NARF特征点提取流程如图2所示。

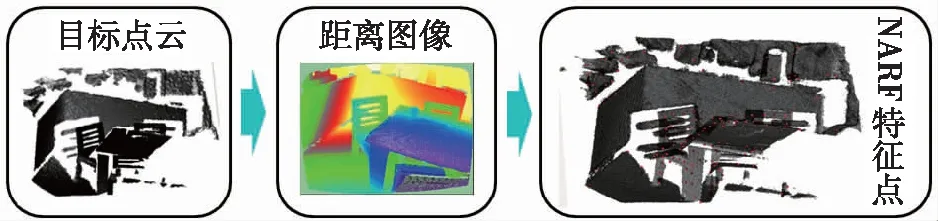
图2 NARF特征点提取流程Fig.2 NARF feature point extraction process

1.2 特征描述

特征描述的作用在于对属于特征点序列中的每一个三维点(pi∈K)进行编码，该编码便于在不同帧之间进行匹配。对于点云配准这一具体应用，选取的关键点要满足以下要求：1)提取的描述子具有一定的抗噪声性能，且能够克服点云低分辨率和不完备性等带来的影响；2)提取的点云具有一定的角度不变性，能够在不同视角下完成匹配。对于要求1)，本文提出将特征点的邻域信息以体素格的数据形式进行表征，以克服噪声带来的影响；对于要求2)，本文使用基于数据驱动的描述子，以保证描述子的旋转不变性。

1.2.1 特征点体素化

对于一个特征点pi∈K，在点云中找到其在半径σ(在本文中σ=0.15m)内的所有领域点：n0,…，nk。以pi为中心构造一个n×n×n的体素格(在本文中n=30)，每个体素格中存储截断距离函数(Truncated Distance Function，TDF)值。TDF值代表了每个体素格中心相对最近的三维点云表面的距离。同时，这些TDF值被截断在1(在点云表面上)和0(远离点云表面)之间。对于体素vi，其TDF值由式(3)进行计算

(3)

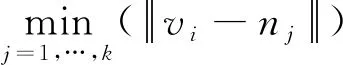
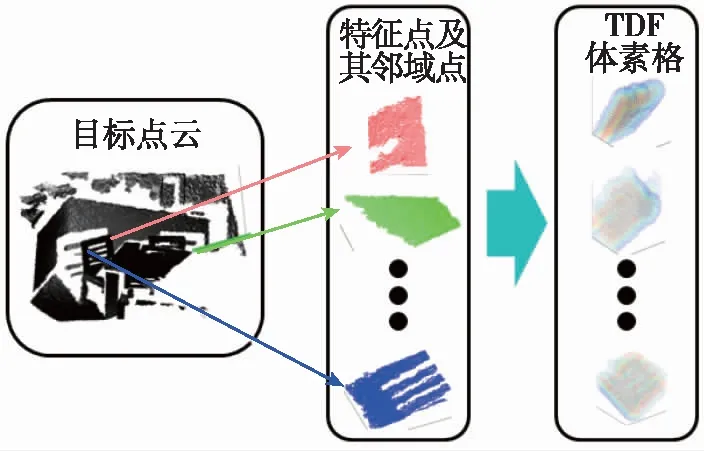
图3 TDF体素格计算流程Fig.3 TDF voxel lattice calculation process

1.2.2 描述子计算

对于每个特征点生成大小为n×n×n的TDF体素格，包含了该特征点的局部几何特征，描述子计算的目的在于给该特征进行编码，以便于后续的特征匹配。受到3DMatch工作的启发[9]，本文使用3D卷积网络对TDF进行特征抽取，网络结构如图4所示。该网络包含8个卷积层和1个池化层，能够将一个303的TDF体素格转化为512维的描述向量(卷积层与池化层的卷积核大小和通道数已标注于图中)。

图4 描述子计算网络Fig.4 Descriptor extraction network

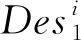
(4)

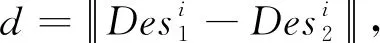
1.3 基于K-d Tree的特征关联

特征关联的目的是在待配准的点云P与Q的关键点子集KP和KQ中找到特征最为相近的点，以完成两帧点云的特征匹配。其本质是一个通过距离函数(欧式距离)在高维矢量之间进行相似性检索的问题， 使用K维树搜索算法能够高效地实现上述过程，该算法的具体流程叙述如下，流程图如图5所示。

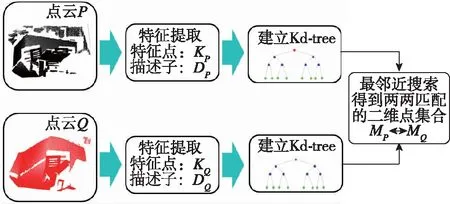
图5 基于K-d Tree的特征关联算法流程图Fig.5 Flow chart of feature association algorithm based on K-d Tree

首先，利用1.1节与1.2节提到的算法分别对点云P与Q提取关键点构成集合KP和KQ，并计算每个特征点的描述子分别构成集合DP和DQ。Kd-tree是每个节点都为k维点的二叉树。由于本文的描述子维度为512维，因此在Kd-tree构建部分对应为根据DP和DQ分别构建512维空间的二叉树，其构建过程可以参考Bentley提出方法[10]中的第3节。

在构建完成Kd-tree之后，分别在DP和DQ中进行最临近搜索，以确定在特征空间中最靠近的特征点，并得到相互匹配的三维点的集合MP与MQ，其实现过程可以参考Bentley提出方法[10]中的第4节。

1.4 基于RANSAC算法的位姿恢复

在基于K-d Tree的特征关联之后，可以得到两帧点云中两两匹配的点云集合。基于上述结果，可以得到目标点云P与点云Q的相对位姿，进一步可以得到点云配准的结果。该算法具体叙述流程如下。

首先，利用1.3节提到的特征关联方法得到两帧点云中两两匹配的三维点集合MP与MQ；然后对于MP与MQ中的三维点，计算2组点的质心坐标p和q；再计算每个点的去质心坐标，如式(5)所示

qi←qi-qpi←pi-p

(5)

(6)

在现实世界中，由于场景和特征的多样性，本来应该一一匹配的MP与MQ不可避免地存在误匹配。考虑到这一情况，本文使用RANSAC[11]机制对MP与MQ的点进行过滤,以获得目标点云准确的位姿。RACSAC机制可以从一组包含局外点的观测数据集中，通过迭代方式估计数学模型的参数。在本文的应用中，可以利用迭代和概率的方法，从有误匹配的数据中估计出点云的相对位姿。引入RANSAC机制的目标点云的位姿恢复算法的伪代码如表1所示。

2 实验和分析

为了充分评估所提方法的性能，本文设计并进行了一系列实验，主要验证以下3个方面:1)所提点云配准方法的成功率；2)所提方法位姿估计的准确性；3)所提方法的配准效率。

表1 基于RANSAC 算法的位姿恢复算法

2.1 实验设置

本文在公开数据集7-Scenes[12]与SUN3D[13]上对所提出的方法进行验证和评估。实验中的几个场景样例如图6所示，每个场景都包含了不同的分辨率、使用不同的重构算法创建。这些场景具备不同的传感器噪声、视角和遮挡方式等情况，能够很好地验证算法。值得注意的是，图中的颜色信息只被用于可视化，在实验中没有用到。

图6 实验数据集Fig.6 Data sets for experiment

本文同时给出了一些参与运算的关键参数和阈值，具体如表2所示。

表2 关键参数设计

2.2 成功率分析

本节对所提出的点云配准算法的稳定性进行了评估，并与传统NARF描述子和ICP算法进行了比较。本文从7-Scenes与SUN3D数据集中选取了8个场景，并从每个场景中选取5对不连续点云(平移和旋转较大)进行配准的评估(一共有40对点云参与评估)。本文使用Choi提出的评判标准判断点云配准是否成功。对于两帧待匹配的点云(Pi，Pj)，如果满足式(7)的条件，则认为算法所估计的Tij是正确的

(7)

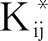
将本文提出的算法与ICP算法、NARF算法进行对比，并将三种算法在数据集上的成功率列举如表3所示。同时，图7给出了数据集中一些具有挑战性的配准案例的示意图，其中第一列为本文提出的配准结果，第二列为NARF配准结果，第三列为ICP配准结果。

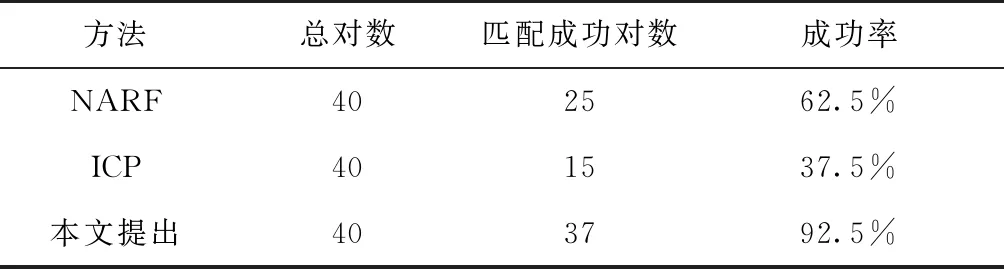
表3 点云配准成功率

图7 配准结果样例Fig.7 Samples of point cloud registration results

实验结果表明：在给定的数据集上，本文提出的算法配准成功率最高。其中ICP算法表现最差，其原因在于数据集中待配准点云稠密且相对旋转和平移较大，该条件不适应ICP算法的工作(点云稀疏且相对旋转与平移较小)[14]。本文提出的算法能够在给定数据集中鲁棒性优于NARF算法的原因在于描述方法的稳定性。在实验中可以观察到，使用本文的描述子进行匹配特征点对数是使用NARF描述子的1.61倍。

2.3 配准精度的比较

本节对所提出的点云配准算法的精度进行了评估，并与传统NARF描述子和ICP算法进行了比较。本文选取了2.2节中各个算法的成功案例进行精度的评估。同样使用RMSE对精度进行评价，定义如式(8)所示

(8)

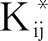
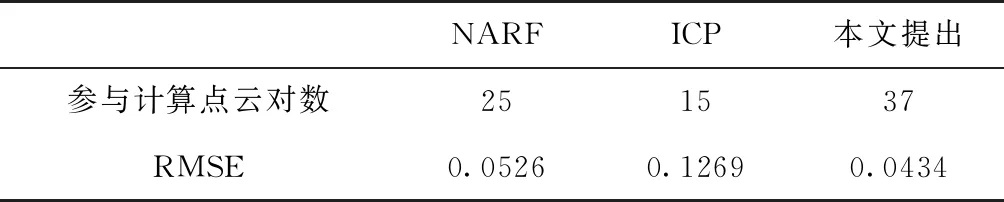
表4 点云配准精度

试验结果表明：在配准精度上，本文提出算法相对使用NARF描述的方法略优，这是由于关键点的稳定匹配的原因。更多的正确匹配点对能够促进更为准确的位姿估计。ICP算法在精度上差于经典算法，其原因在于：由于点云的稠密性，ICP算法在最优结果的邻近位置难以找到正确的对应点对，导致无法进一步迭代优化。

2.4 配准时间的比较

本节对所提出的点云配准算法的效率进行了评估，并与传统NARF描述子和ICP算法进行了比较。本文进行实验的计算机平台的软件硬件环境列举如表5所示。

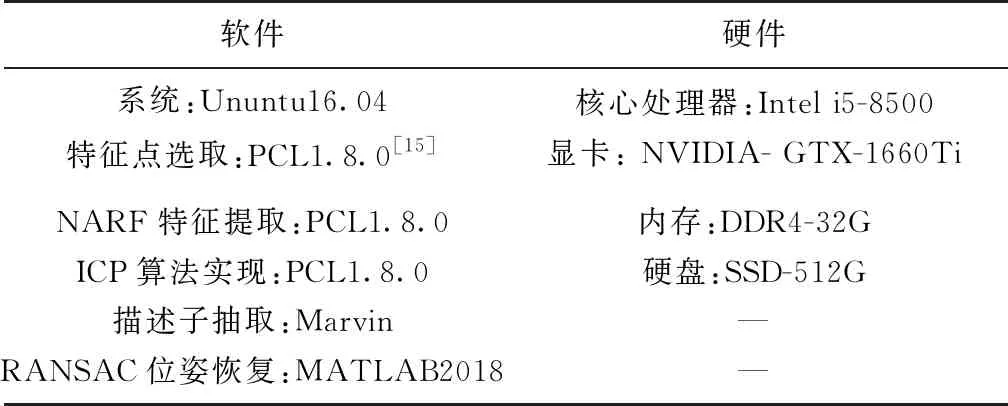
表5 实验条件

本文同时统计了三种算法在该环境下进行点云配准的平均时间，结果如表6所示。

表6 配准时间比较

试验结果表明，在稠密点云上，基于特征匹配方法的配准时间优于基于迭代算法。本文提出的算法在数据集上能够基本做到10.7021s/帧的配准速度，与NARF基本在一个水平。

3 结论

随着点云传感器的发展，三维点云数据的稠密性和测量精度将会在未来得到显著提高。本文提出了一种基于点云局部几何特征的稠密点云配准方法，探讨了将基于深度学习的点云描述子运用于点云配准的问题。实验结果表明，针对稠密非连续点云的配准问题，基于特征匹配的方法在效率和精度上都优于基于ICP的方法；同时基于数据驱动的点云描述子在不损失配准精度的情况下，鲁棒性明显优于手动设计的点云描述子。

该算法目前存在的问题有：为保证实时性需要GPU的支持、描述子提取需要进行前期训练等。在未来，我们将改进算法，使之可进一步应用于不同类型的点云(激光雷达)；同时提升算法的实时性，将其应用于重定位、轨迹推算、回环检测等问题中。