基于广义回归神经网络的全球表层海水1°×1°二氧化碳分压数据推演

钟国荣，李学刚，曲宝晓，王彦俊，袁华茂，宋金明

( 1. 中国科学院海洋研究所 海洋生态与环境科学重点实验室，山东 青岛 266071；2. 中国科学院大学，北京 100049；3. 青岛海洋科学与技术试点国家实验室 海洋生态与环境科学功能实验室，山东 青岛 266237；4. 中国科学院 海洋大科学研究中心，山东 青岛 266071)

1 引言

当前的研究普遍认为大洋每年可以吸收约2 Pg（以碳计）左右的大气CO2，这一结果主要是通过海−气二氧化碳分压差估算出来的，并且与模式的估计也相一致。但用分压差估算出的结果仍有很大的不确定性，主要原因是二氧化碳海−气交换速率的不确定，以及参与计算的表层海水二氧化碳分压（pCO2）的数据较少且空间分布不均匀[1–3]。尽管pCO2实测数据相对一些其他参数比较容易获得，可以通过基于非色散红外法的船舶连续走航观测获得[4]，但获得的实测数据相对于整个大洋来说仍然较少，这使得通过集成多年的数据构建气候态分布成为过去比较有效的研究方法[5]，但要获得大范围区域pCO2的连续时间变化用一般的空间插值法仅依靠这些实测数据是远远不够的。并且实测数据在时空分布上也非常不均匀，特别是早期20世纪70年代前的实测数据几乎没有，这极大地限制了基于pCO2演化有关的大洋碳循环研究的时空尺度。虽然美国国家航空航天局(NASA)、欧洲多国合作观测项目（EPOCA）等一直在着手扩展海洋观测网络，但巨大的资金投入换来的也是十分有限的时空覆盖范围。在这个背景下，通过大数据技术利用仅有的少量观测数据和一些辅助参数，构建均匀的大洋pCO2格点数据来研究全球变化成为新的突破方向。有研究者尝试利用传统的多元线性回归来重建二氧化碳分压变化，但其结果只适用于有限的特定区域[6]，甚至只适用于特定季节[7]。相比之下机器学习算法和人工神经网络更具有优势，可以通过实验建立起大量参数间的实证关联，来更准确地反映复杂的海水系统中pCO2的变化规律[8]。机器学习算法包括随机森林算法（Random Forest Algorithm，RFRE）、支持向量机（Support Vector Machine，SVM）等，目前的研究也多局限于单一过程主导的小范围区域，对复杂区域及全球范围的预测则显得比较乏力。人工神经网络种类很多，现有研究中利用的有前反馈神经网络（Feed forward Neural Network，FFNN）[9–10]、自组织映射神经网络（Self-Organizing Map，SOM）[11]等，目前仍存在较大的不确定性，其标准误差从17.6 μatm到20.2 μatm不等[12–13]。广义回归神经网络（General Regression Neural Network, GRNN）是FFNN中径向基网络的一种变形形式，与传统的前反馈网络相比，GRNN是非线性拟合能力特化的形式，在各个学科和工程领域应用都更加广泛。GRNN无需传统的改变神经元间连接权值的训练，只需要对一个光滑因子寻优，训练速度比FFNN快几十到上百倍，对数据预测的连续性也优于SOM的离散估计。为了获得误差更低的高时空分辨率全球表层海水pCO2数据，本文首次尝试了将GRNN应用于表层海水pCO2格点数据的推演。

2 数据来源

研究使用的表层海水二氧化碳分压实测数据来源于表层大洋二氧化碳地图（Surface Ocean CO2Atlas,SOCATv2019）数据集，该数据集由超过100个成员组成的国际海洋碳研究组织组建，对实测数据进行了质量控制后公开发布。整个数据集包含约2570万条观测数据，时间范围为从1957−2018年。由于受叶绿素浓度数据的时间范围限制，我们只使用了1998−2018年的数据。数据的总数量分布如图1所示。实测数据的分布十分不均匀，整体上北半球数据覆盖率和数据总量都高于南半球，欧洲、日本与美国东部沿岸等少数区域数据总量超过10万条，而印度洋、南太平洋和一些近岸区域20年间数据总量只有100到1000条左右，不到10条甚至没有数据的区域也占不小的比例。在时间分布上不均匀的程度更加明显，如图2所示的最近20 a获得的pCO2调查数据，以后10 a数据量多，数据覆盖范围更广，而前10 a数据量少，覆盖范围也小。

图1图例中n为数据的数量级，代表格点位置中有10n条实测数据，灰色部分代表格点位置中无实测数据。

图1 1998–2018年间SOCAT二氧化碳分压数据分布情况Fig. 1 Spatial distribution of pCO2 observations in SOCAT dataset from 1998 to 2018

图中实测数据覆盖范围指有实测数据的网格数占海洋区域总网格数的比例，1°×1°经纬度的分辨率下，海洋区域总网格数约为43000个。

在SOCAT数据集中给出的是二氧化碳逸度（fCO2），在使用时将其转换成二氧化碳分压，以便与其他研究或数据集进行对比验证，二者间的换算关系为[14]

式中，R为气体常数（8.314 J/（K·mol））；p为大气压（单位：Pa）；T为绝对温度（单位：K）；B和δ为校正系数（单位：m3/mol），计算式为

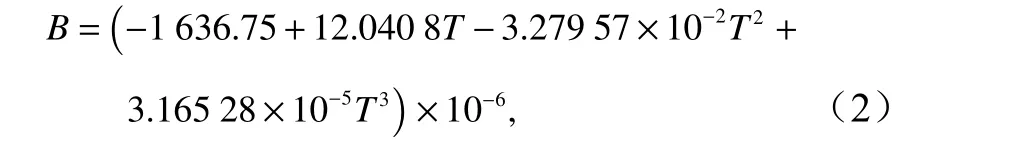
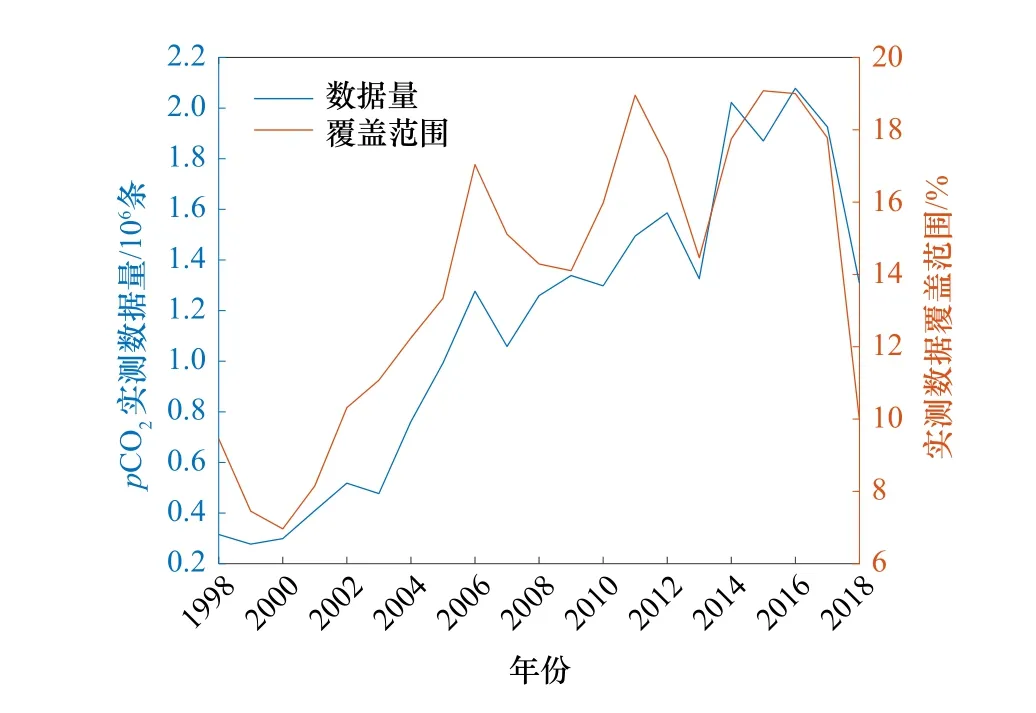
图2 SOCAT pCO2实测数据时间分布Fig. 2 Temporal distribution of pCO2 observations in SOCAT dataset

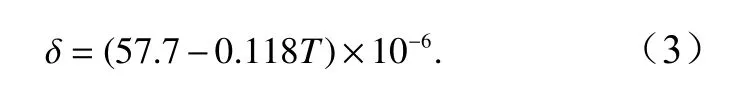
理论上，表层海水二氧化碳分压主要受海水的热力学性质、生物活动和物理过程控制。在新构建的方法中，选取了与这些过程紧密相关的温度、盐度和叶绿素浓度，加上与时空连续性相关的经纬度、时间等参数作为推演pCO2的辅助参数。这些辅助参数的实测数据时空覆盖范围决定了生产出的格点数据的时空覆盖范围，因此在相关性高的条件下，应优先选择实测数据多的参数。本方法中使用的表层海水温度与叶绿素浓度为卫星遥感数据，具有足够大的空间范围和足够长时间的连续观测。通过建立与这些参数间的非线性关系来推演表层海水二氧化碳分压变化：

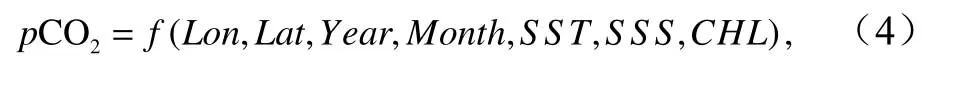
式中，Lon、Lat为经过三角函数换算的经纬度，经度为0°～360°制，以保证数据在空间上的连续性。Year、Month分别为数据对应的年和月；SST、SSS分别为表层海水的温度（单位：℃）、盐度；CHL为叶绿素浓度（单位：mg/m3）。使用的所有参数实测数据来源如表1所示。

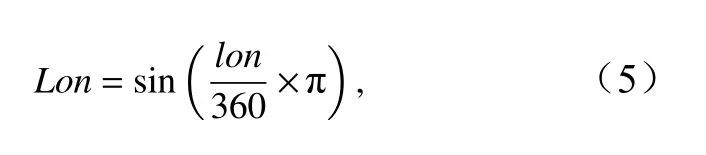
表1 数据来源Table 1 Data source

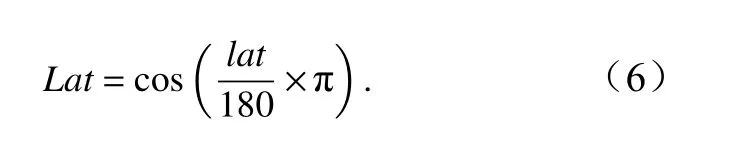
3 格点数据构建方法

3.1 广义回归神经网络原理

广义回归网络是Specht[15]在1991年建立的一种径向基网络的变形形式，和径向基网络一样具有良好的非线性问题处理能力，并且训练更为方便。将训练样本作为后验条件，在Parzen非参数估计的基础上，广义回归网络计算输出时遵循最大概率原则[16]。

假设神经网络的输入和输出分别为X和Y，联合概率密度可表示为f(X,Y)，以X0代表训练集的观测值输入，Y相对X的回归为

输入X0时，神经网络的预测输出为Y(X0)。给出训练样本数据集X0与Y0的情况下，利用Parzen非参数估计对密度函数f(X0,Y)进行估算并化简可以得到：

式中，n为样本总数，l为输入变量X的维数。σ为光滑因子，等同于高斯函数中的标准差。Xi代表第i个计算样本对应的神经网络输入，Yi代表第i个计算样本对应的神经网络输出；X0j代表训练样本数据集输入X0的第j个维度，Xij代表第i个计算样本对应的输入Xi的第j个维度。

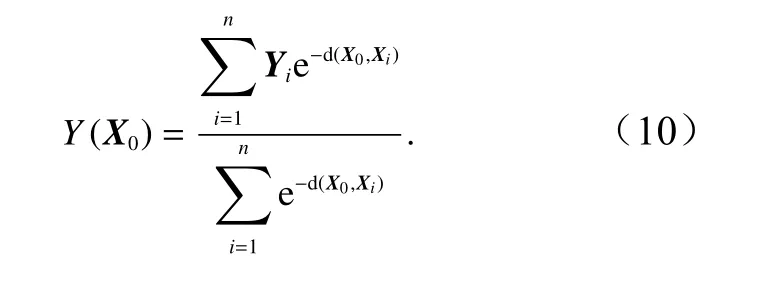
式（10）即为广义回归神经网络计算出的预测值，其分子为训练集中所有样本求出的Yi的加权和，权值等于 e−d(X0,Xi)。

从结构上看，广义神经网络分为4层：输入层、隐含层、加和层和输出层(图3)。

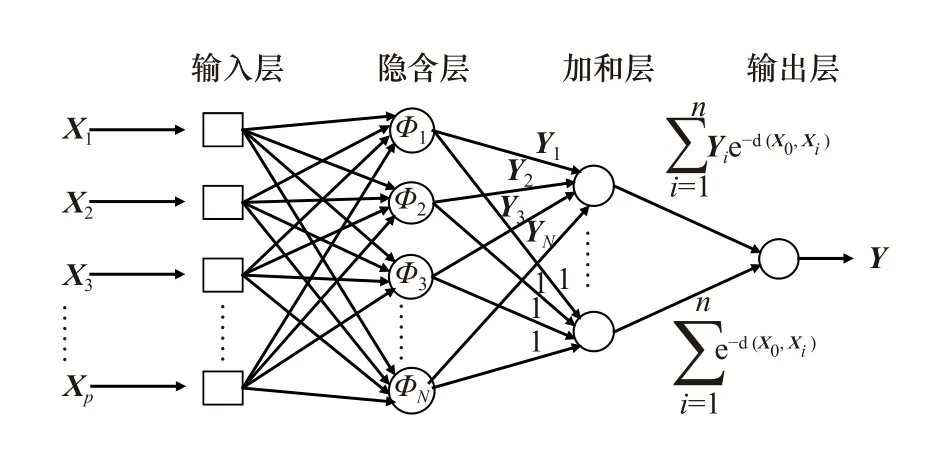
图3 广义回归神经网络结构Fig. 3 Structure of general regression neural network

输入层即负责接收样本数据的输入向量X，神经元数量与输入向量X的维数l相同，以简单的线性函数作为传输函数。其中维数l等于7，即输入包含7个维度，分别为经度、纬度、年、月、海表温度、海表盐度和叶绿素浓度。一些研究中时间仅使用月或者仅使用年作为辅助参数，但同时使用能略微降低整体的误差，因为增加了输入向量的维度，而且这对计算时间影响很小。隐含层的神经元数量为驯良样本数量，通常使用高斯函数作为基础函数，Φi代表第i个隐含层神经元，其中心向量为对应的输入向量Xi。加和层的神经元只有两种，分别为分子单元和分母单元。分子单元将训练集样本的输出期望作为权值，求得隐含层神经元的加权和，即式（12）中的分子部分，分母单元负责的是隐含层神经元的代数和，即式（12）中的分母部分，分子单元和分母单元的输出在输出层中相除即得到输入X对应的预测输出Y。

3.2 网络训练与插值

为快速检索，原始实测数据根据时间和经纬度存储在细胞数组中，时间分辨率为12月×21 a，空间分辨率为1°×1°经纬度，对神经网络进行训练时需要先将格点化的数据集转换成向量，再将其输入到网络中，过程如图4所示。

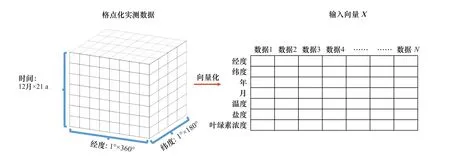
图4 原始数据向量化过程Fig. 4 Vectorization of original data

训练使用的样本数据集为1998−2018年的所有数据中随机抽取的80%，由于数据总量大，并且格点数据构建的目标最小时间分辨率为1个月，对同1个1°×1°格点里同1个月内的pCO2实测数据进行了算术平均化处理。GRNN程序通过MATLAB自带的广义回归神经网络函数工具箱实现，网络的创建、训练和插值计算均可以通过工具箱函数命令进行。其中训练过程在创建的同时完成，函数语法为

式中，X0、Y0分别为训练集的输入和对应的期望输出，X0是经度、纬度、年、月、温度、盐度、叶绿素浓度实测数据组成的向量，Y0是pCO2实测数据组成的向量；net为网络名，在同时存在多个网络时用于辨识；newgrnn为MATLAB自带的广义回归网络工具箱函数，用于创建并训练网络。spread为扩散速度，是人为设定的固定标量，默认为1.0，其值越大拟合出的曲线越平滑，但如果想更精确地接近训练样本的期望输出，应该选择较小的扩散速度值，经过多次试验后我们择优选取的值为1.4。广义回归网络的训练过程目的是为了求得式（9）中光滑因子σ值的最佳值，这个值很大程度地影响网络的性能。当σ值非常大时，d(X0,Xi)趋近于0，计算出的输出Y(X0)近似于所有训练集样本输出的平均值；当σ值趋近于0时，神经网络会出现过学习的现象，表现为给定的输入与训练集中某一数据相同时，计算得到的预测输出与实测值非常接近，但给出的输入不在训练数据集中时，计算出的输出与实测值偏差较大。避免这各种情况出现的方法是对输入的各个参数量级进行调整，保证各参数变化范围的数量级不相差过大。在我们使用的输入参数中，除年份外的参数均在0～40间变化，因此将所有数据的年份的数量级调整到与其他参数一致：

调整后年份的变化范围为1～21，这样就避免了过学习现象的出现。

创建并训练网络后，输入二氧化碳分压空白区域对应的温、盐等参数组成的向量X，即可计算出预测的二氧化碳分压值Y，函数语法为

式中，net和创建时的net为网络名，可替换为其他名称，但两个过程的名称必须保证一致。在这个计算过程中，输入的向量X包括了所有待插值的格点，不需要每个格点单独计算。最后再将输出的二氧化碳分压预测值向量Y还原成180°×360°大小的矩阵，存储到细胞数组中，插值方法结束。

4 构建数据的准确性分析

由于在插值方法训练时仅使用80%的实测数据，剩余的20%实测数据就可用于对方法进行准确性评估。这20%实测数据在训练完成后输入到神经网络中，比较实测值Y0和神经网络计算出的预测值Y的差异来评估所构建数据的准确度。通常用标准误差（RMSE）和平均相对误差(MRE)来描述方法的精确度。

其中标准误差的计算公式为

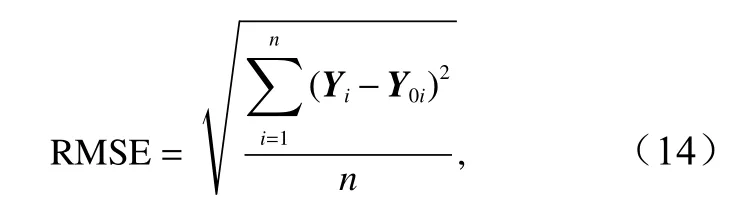
式中，Yi代表第i个样本的pCO2神经网络预测值，Y0i代表第i个样本的pCO2实测值，n为进行误差评估的测试样本总数，参与神经网络训练的数据不用于误差评估。标准误差对一次预测中的特大或特小误差十分敏感，反映出预测值相对于实际值的偏离程度，是用于评价拟合效果的指标中最常用的。

平均相对误差的计算公式为对每个点误差占实测值的比重求平均：

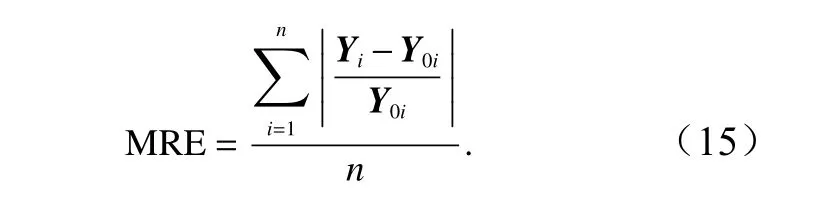
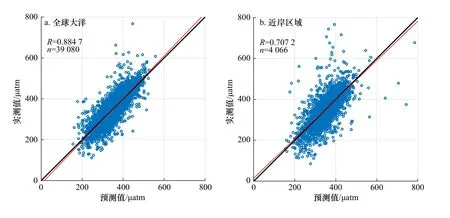
对比广义回归网络计算出的预测值Y和实测值Y0可以发现，预测结果与实测数据基本一致。以Y为x轴，Y0为y轴作图，绝大部分数据点聚集在y=x直线处，部分偏离较远但仍均匀地靠近直线并分布在直线两侧（图5），回归线也十分逼近y=x直线。全球大洋的预测值相较于实测值的平均相对误差为2.97%，标准误差为16.93 μatm，相关系数为0.8847。实测数据多的区域，如亚热带太平洋、赤道太平洋和亚热带大西洋，插值预测的表现最好，标准误差为10.45～13.87 μatm，平均相对误差为1.93%～2.66%。南太平洋数据量较少，误差却也很低，可能是因为数值变化范围较其他区域小，实测pCO2值均在250～450 μatm之间，而不管哪个区域在这一区间内的预测值与实测值都很接近。表2给出了与其他方法的标准误差对比[11–13,17–21]，在整体上，GRNN略优于FFNN与SOM，具体到特定区域范围时，一些机器学习算法的表现可能更加精确，例如Chen等[17]使用随机森林算法重建了墨西哥湾的pCO2变化，标准误差仅9.10 μatm，然而仅适用于主导因素较为单一的小范围区域。也有研究将SOM和FFNN结合在一起，利用SOM将大西洋划分成多个区域，对每个区域训练一个FFNN来进行插值预测[20]，但精确度并没有显著提升，并且由于同时使用了两种神经网络，应用起来更加繁琐。近岸区域由于受到陆地径流和人类活动等因素影响，规律十分复杂，广义回归网络做出的预测表现与大洋区域相比较差，但相近于Laruelle等[21]使用SOM-FFNN法对近岸区域的预测表现。如果包含近岸区域，整体的标准误差将上升到21.60 μatm，但其他的研究也只关注大洋区域，或者只关注近岸区域，并没有统一研究。

图5 广义回归神经网络预测值与实测值对比Fig. 5 Comparation of GRNN predict pCO2 and in situ measurements

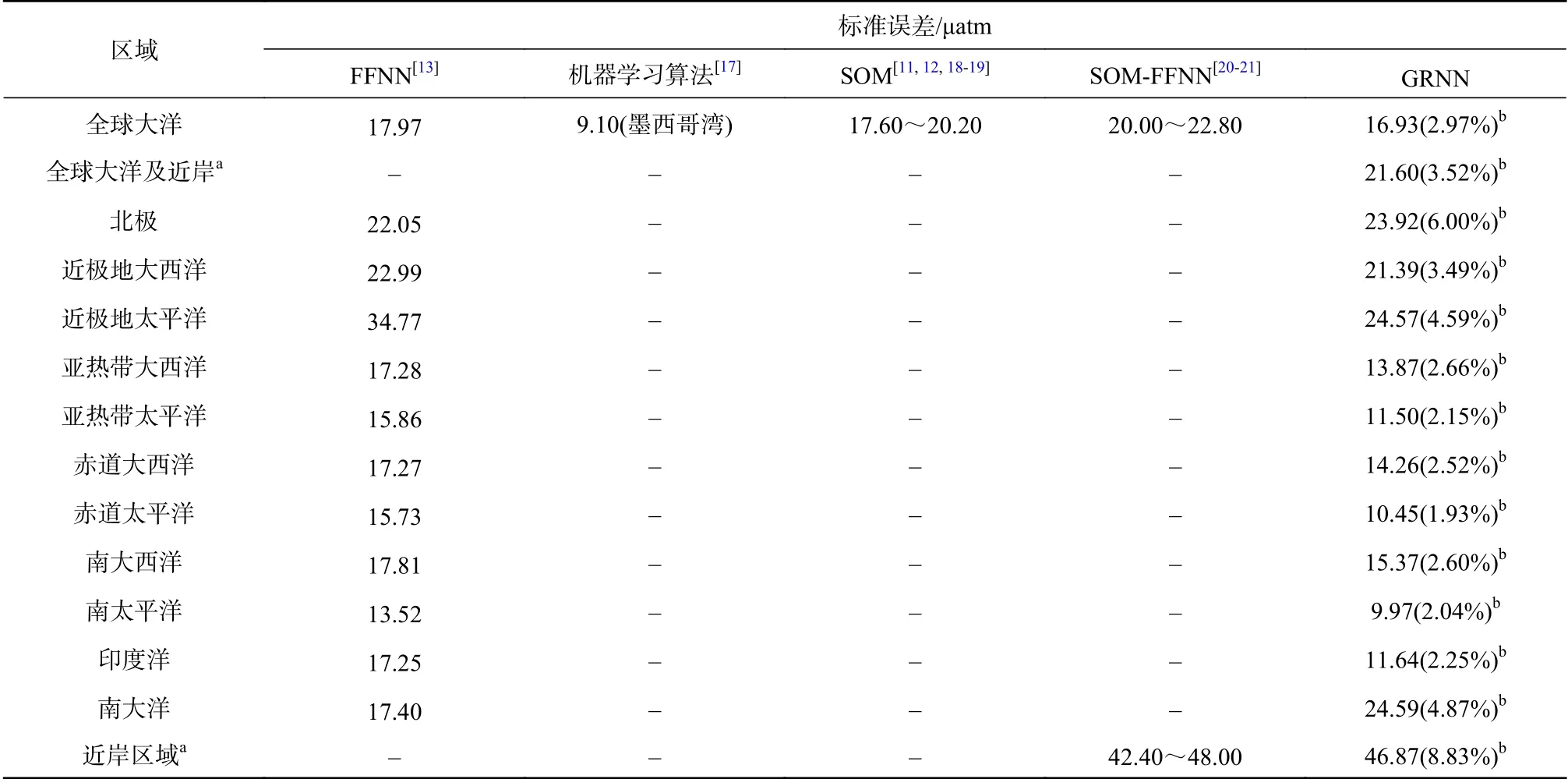
表2 GRNN与其他方法误差对比Table 2 Comparation of errors between GRNN and other approaches

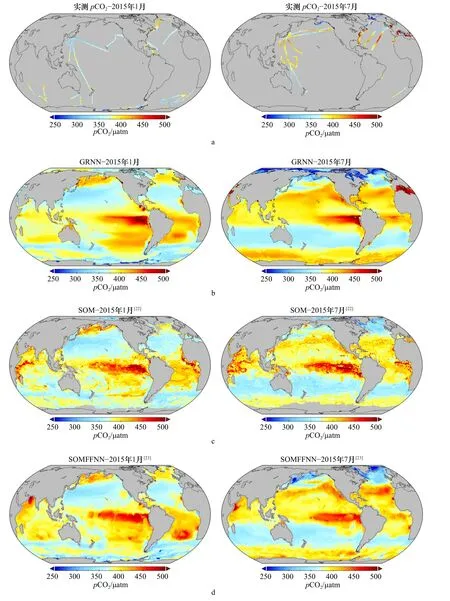
图6 GRNN与实测值及其他神经网络方法同时间点pCO2数据结果对比Fig. 6 Comparation of pCO2 distribution between in situ measurements, GRNN and other approaches

尽管存在一定的误差，GRNN法的结果与pCO2实测值的分布在高值和低值区域的位置上基本一致（图6a，图6b）。与同样使用SOCAT数据集的其他神经网络方法的数据产品进行对比(图6b至图6d)，图6c为SOM法，标准误差为23.3 μatm，图6d为SOM−FFNN联用法，标准误差为22.8 μatm，几种方法整体的季节趋势表现出高度的一致。在1月份，南半球中纬度海域pCO2高，南太平洋东部高于西部；北半球中纬度海域整体pCO2低，而北太平洋和北大西洋近极地区域与中纬度区域相反，pCO2高。7月中纬度海域整体分布规律与1月大致相反，南大洋pCO2高，北极区域低，这些特征都与其他方法给出的结果相一致。尽管使用的实测pCO2数据集一致，不同方法使用的辅助参数种类也不同，例如图6中另外两种方法中，图6c使用的参数中没有经度，使用了混合层深度，图6d没有经纬度和时间，这可能也是特定区域的pCO2分布规律上各有差异的原因，特别是印度洋等实测数据少的区域。此外，不同研究使用的辅助参数空间覆盖范围不同，导致构建出的pCO2空间范围存在差异。不同类型的神经网络本身的特性也存在差异，由于SOM给出的是离散的估计，数据的空间连续性最差，存在明显的斑块状分布。SOM-FFNN虽然是连续的估计，但是数据过渡也不太平滑，锐利的边界仍存在。而表层海水并不是相互独立的，由于物理混合过程的影响，高分辨率的情况下相邻网格间月平均pCO2不应该相差太大。比起其他方法，GRNN法推演出的数据平滑程度更高，不需再进行人为的二次处理来达到平滑过渡效果，有潜力应用于更高分辨率的数据构建上，如0.25°×0.25°甚至更高。

除了神经网络法外，与Takahashi等[24]通过将数十年的实测数据校正到同一年，构建气候态分布的方法对比，pCO2的整体分布规律也存在较高的一致性。如图7b是Takahashi等[24]的研究中给出的校正到2005年的1月pCO2全球分布，图7a是同时间GRNN法给出的结果，北太平洋的高值带和低值带、南大洋的低值区域等非常相似。尽管使用的源数据和方法本身上存在一些差异，使不同研究的结果在具体的区域分布各有不同，但整体的分布规律高度相似，结合标准误差和平均相对误差来看，有足够的理由相信广义回归神经网络在二氧化碳分压的插值预测上是可靠的。

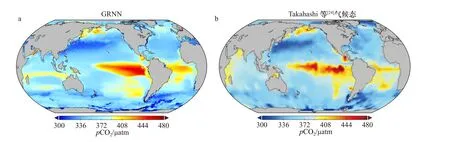
图7 GRNN法与Takahashi等[24]气候态pCO2数据对比（2005年1月）Fig. 7 Comparation of pCO2 distributions between GRNN output and Takahashi[24] climatological mean (January, 2005)

5 结论

基于广义回归神经网络，建立了表层海水二氧化碳分压与经纬度、时间、温度、盐度和叶绿素浓度间的非线性关系，并据此重建了近20年来表层海水二氧化碳分压的全球分布，标准误差为16.93 μatm，平均相对误差为2.97%。与其他方法的对比证实了本插值方法的可靠性，并且广义回归神经网络法的适用性更强，对近岸区域也能做出预测，其表现与只关注近岸区域的其他研究相近，网络训练的速度也远高于其他神经网络。使用广义回归网络进行插值预测时，由于不需要设定扩散速度外的参数，插值结果的表现主要受实测数据本身影响。在参数选择方面，输入参数对神经网络的预测表现影响很大，但增加相关性低的参数并不能提高精确度，反而会降低输出数据的平滑度，导致分布呈现斑块状，并且会增加计算时间。虽然增加相关性高的参数可以显著地提高精确度，但受该参数可获得性的极大限制。例如本研究在pCO2参数的构建中选用的叶绿素浓度，该参数与pCO2有较高的相关性，但由于仅能获取该参数在1998年以后的大量卫星遥感数据，也仅能用该参数重建1998年以后的pCO2数据，而由于无法获得足够的1998年之前的数据，就无法用本研究建立的插值方法重建1998年之前的pCO2数据。现有研究也大部分是通过使用卫星遥感数据来解决参数可获得性的问题，但满足条件的卫星遥感数据也只有最近几十年的，这也是大部分现有研究都只能重建近几十年pCO2数据的原因。而更早期的观测数据过少，很难支撑大范围的预测插值，因此如何重建早期的pCO2数据成为待解决的下一个难题。