时变网络下轨道交通出行路径动态选择模型——以武汉市为例*

王 冠 钟 鸣 李建忠 孙贻璐

（1.武汉市交通发展战略研究院 武汉430017；2.武汉理工大学智能交通系统研究中心 武汉430063）

关键字：轨道交通；路径选择；换乘模型；时变网络；概率空间；武汉市

0 引 言

截至2018年底，大陆已有35个城市运营轨道交通，线路总长5 761.4 公里[1]。基础设施不断完善的同时，出行需求水平亦同步增长，国内外先进经验表明城市交通发展已步入设施建设与科学管理的并重阶段[2]。通过充分搜集、挖掘信息，反映规划、建设和运营所关注的问题，是轨道交通发展的必然趋势[3]。但动态变化的出行需求与设施建设及运营管理之间缺乏强耦合关联，比如由闸机刷卡记录提取的进出站点客流无法有效支撑换乘通道设计与运营方案制定，设施供给能力瓶颈和静态运营方式或许导致高峰期存在安全隐患[4]。

针对轨道路径选择问题，国内外学者们开展了一系列有意义的研究工作。吴祥云等[5]采用Frank-Wolfe 算法求解了基于用户平衡原理的客流分配模型。四兵锋等[6]提出了反映轨道出行成本的广义费用函数，建立了影响轨道网络客流分配的主要因素与路径选择Fisk模型。基于Logit模型，刘剑锋等[7]提高了广义费用对选择概率的影响效力。林湛等[8]增加了随机扰动项，并通过幂函数表达累积换乘效用。陈坚等[9]定义了开销系数，用于表征乘客对车内拥挤的心理感受。

轨道出行群体是由若干异质性个体组成，不同个体的选择行为均不同。基于此，黄婷婷等[10]研究了几类不同年龄、职业、出行目的乘客对路径选择影响因素的理解，但通过调查无法考虑各类群体的出行特征与换乘影响因素之间的关系。已有研究将车内拥挤情况作为路径选择因素但未影响上车决策。基于此，钱堃等[11]在广义出行成本中考虑了高峰期因车内拥挤导致乘客无法上车的情况，依据调查或经验获取参数。另一方面，现有成果主要使用静态站间距离表征出行网络载体的权值，简化处理运力配置和发车间隔变化对路径选择的作用。基于此，Zhang等[12]引入了轨道运营时刻表，Zhao等[13]补充了随机因素。但群体聚集对个体出行的影响还未详细阐述，尤其在出行对供需关系随时间演化的响应方面。

上述工作引发3 个值得关注的问题：①不同群体的选择行为与特征均不相同，应整体研究群体的相互作用，并独立处理个体的出行特征；②出行路径的影响因素还应与运力配置、发车班次等运营模式密切相关；③车内拥挤情况应随客流影响量因时而变，且时变的拥挤度感受应直接影响出行决策。本文基于复杂网络理论，将轨道站点作为网络节点，站间实际列车运行时间作为节点间联系，按照一定规则将全天划分为若干时段，建立了时变的运行载体网络，精细化模拟出行路径选择环境。同时，考虑到车内客流量的实时变化特征，形成了基于站间断面的全网出行需求与承载容量的动态演化模型。

1 基于供需关系的时变网络环境

在地理空间视角下，轨道网络属于静态指标，在一定的建设周期内，其站点布置、线路走向、换乘设计等均属于固定标量。然而在完整的轨道运行体系视角下，规划建设完成之后，线网环境不仅是出行活动的载体，也是运营管理的对象，网络在二者的共同作用下因时而变，乘客出行在时变的供需环境中。

1.1 需求方面

城市空间布局与出行目标的差异，影响轨道出行总体呈现2 种不均衡性，引起需求水平实时变化：①出行时间分布不均衡，全网高峰期进出站客流量一般是平峰期的2～3倍；②客流空间分布不均衡，城市内环核心区的进出站客流明显高于外围区域，线路各站点的客流呈现极大的峰值错位和量级差异。

1.2 供给方面

管理者从运营角度制定措施应对需求变化，主要包括调控发车间隔、设定大小交路等，导致网络供给能力变化各异。以武汉市2个轨道断面为例说明（见表1），在高峰期和平峰期，列车运行时间和站点驻留时间差异不大，但换乘步行时间与换乘候车时间差异较大，并且随着路径断面累积效应叠加，差异逐渐放大。

表1 武汉市2 处轨道断面不同时段出行时间差异对比Tab.1 Difference of travel time between two rail sections during different periods in Wuhan

因此，即使是每天相同起终站点的通勤出行，也不会运行于完全一致的网络环境中。同时出行需求波动和运营供给调节共同引起车内拥挤水平相应变化。本文以此为背景，充分考虑乘客的出行自主性，建立路径动态选择模型。

2 路径动态选择模型

轨道换乘的本质是乘客对出行路径的选择，其可测结果为换乘站点与站间断面的客流量，由隐含的路径效用决定。在信息充分的情况下，乘客对出行路径选择具有极高的自主性，是基于自身需求与外部环境动态选择的结果。动态选择主要表现为2个方面：①出行成本与时变的网络环境相关；②拥挤度感受与时变的运载水平相关。本节建立路径动态选择模型，包括影响要素、分时效用、出行成本和概率选择等方面。

2.1 影响要素

城市轨道票价一般采用里程计费，对于1 次出行，乘客选择任意路径所支付票价相同，因此经济成本不作为模型影响要素。根据调查结果，乘客选择出行路径时，主要关注行车时间、换乘便捷性与舒适度感受等。行车时间指出行的车内时间，包括列车运行时间和列车站点驻留时间。换乘便捷性由换乘设施与线路运力服务效率决定，影响出行的换乘时间，包括换乘步行时间与换乘候车时间。舒适度感受主要由车内拥挤度反映，属于主观感受，作用于列车运行全程。

不同时段、不同区域、不同类型的出行群体，对各要素重要性的认知亦不同。调查得知，高峰期的通勤群体更加关注出行时间，而非高峰期的其它人群偏向于舒适度感受；中心城区客流考虑能否在高峰期顺利上车，而新城区客流关心在非高峰期需要候车多久。本文将时间作为各要素的共同属性，用于量化出行成本。

2.2 分时效用

在时变的网络环境中，各类要素呈现不同特征且相互交织，其中客运压力对时间更为敏感。本文以站间断面为基础单位，按照一定的时间粒度m 分钟，将全天进站记录划分为n 个( )1 ≤i ≤n 计算周期，每个周期内的个体出行按照进站时间载入个周期（T 表示1次出行允许的最长时间，|·|表示取整数操作），则每个周期内的进站客流量影响其后连续个周期内的网络客流量。第i 个周期的断面客流由周期i-3，i-2，i-1等决定，见图1。

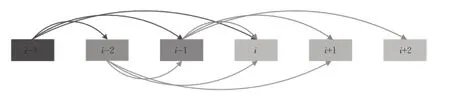
图1 轨道网络第i 个周期的拥挤情况由其紧前的若干周期决定示意图Fig.1 Congestion in the period i of the rail network is determined by some preceding ones

2.3 出行成本

在时变网络结构中，考虑个体的出行偏好。对于某OD中选择路径的第l 个断面（共计L 个），建立基于车内时间、换乘时间与拥挤度感受的广义出行成本

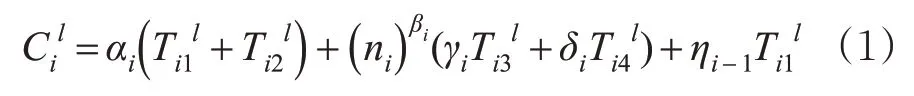
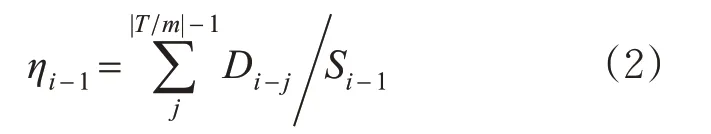
式中：Di-j表示第i 个周期之前个周期内的未出站客流量，Si表示第i 个周期的车内荷载量。对于某OD 在第i 个周期的路径广义出行成本为

2.4 概率选择

网络化运营环境下，任意站点OD 存在多条出行轨迹。基于广义出行成本，可计算出第i 个周期的最优成本。真实轨道运行中，既不会全体均按最优成本出行，也不可能穷举所有可能。

因此，笔者计算每个OD的K 条可行路径，其中第k(1 ≤k ≤K )条路径的广义出行成本与最优广义出行成本之间满足关系

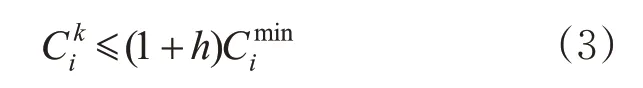
式（3）中设定参数h 用于控制计算路径的实际交通可行性[8，11]。运用Logit 函数将上述K 个标量映射到概率空间，其分布满足

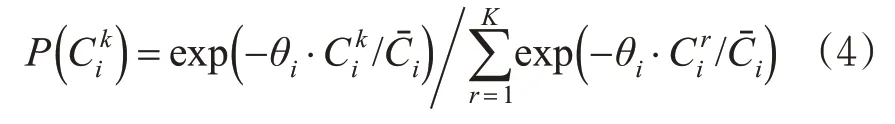
上述讨论表明，各类基于目标最优的单概率搜索方法属于多概率选择方法的特例，存在一定的保守型。基于概率的分时模型考虑了各种出行的可能性，为不同时间下的站台容量设计、断面流量管理、客流趋势研判提供了量化依据。

3 模型实现与指标获取

以武汉市2019年上半年运营线网为对象，依托调查数据、运营数据、刷卡数据等，标定模型参数，分析参数灵敏度，改进搜索算法获取客流运行指标。

3.1 模型参数分析

1）数据收集。模型需要4类基础数据：①轨道线网静态信息；②全网列车运营信息，包括发车班次、到离站时间、运营编组等；③对应的全网乘客进出站刷卡记录，包括进出站位置和时间等；④调查数据。其中调查完成以下3个方面工作。

（1）基本信息调查。该项调查共发放表格5 600份，回收有效表格4 963份，有效率为88.6%。调查内容包括乘客的年龄、职业、出行目的、出行时段、认为影响换乘的因素、期望的换乘时间，对轨道运行信息的获取程度及渠道、以及对换乘的意见等。该项调查用于获取宏观层面的信息，确定共性参数。

（2）换乘路径调查。以“金银潭—江汉路”区间出行为研究对象，在2/6 号线换乘站江汉路站专题调查集散于该站点的乘客，寻找其中到发于金银潭站的群体。全天共计采集到221 份有效样本，其中94.1%选择采用2号线直达，而5.9%选择2/6号线换乘（包括1次和2次换乘的情况）。

（3）换乘时间调查。在不同时段，调查员记录换乘通道的平均步行耗时。影响换乘步行时间的主要因素是所在时段换乘通道的客流承载情况，以及换乘电梯的使用效率。上述2项调查用于获取微观层面信息，确定模型参数。

轨道“金银潭—江汉路”区间涵盖了不同的断面客流强度、不同的线路运营模式（大小交路）、不同的换乘路径，不同的首末站进出口等。该区间提供了时变的网络环境和车内拥挤水平，以及多换乘路径选择等条件，满足模型研究要求。

结合上述调查结果和运营信息，分别在早高峰、午间平峰、晚高峰和晚间平峰内统计各路径真实出行与期望出行时间平均值，见表2。

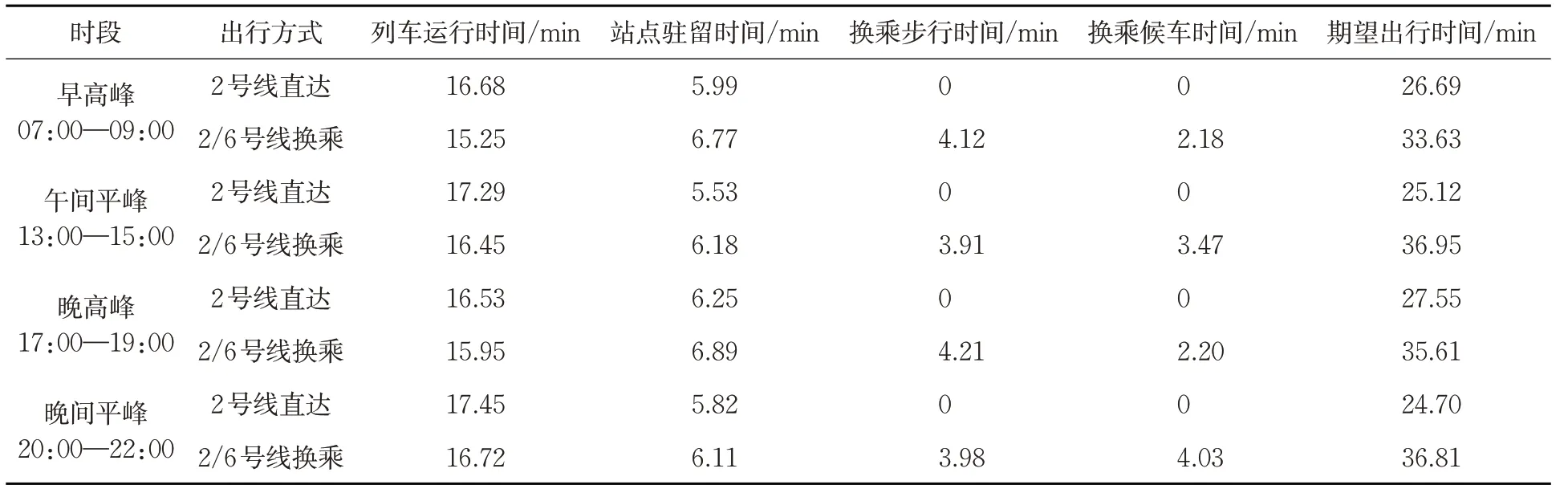
表2 工作日武汉市轨道“金银潭—江汉路”区间不同时段真实出行与期望出行时间平均值Tab.2 Average values of actual travel time and expected travel time during different periods of“Jinyintan—Jianghan Road”section on weekdays in Wuhan

2）参数标定。将式（1）对数化线性处理，采用最小二乘法拟合模型参数。如图2 所示，车内时间权重α 在高峰期大于平峰期，而换乘时间权重β，γ，δ 正好相反。进一步说明高峰出行关注占比更高的车内时间，而平峰出行更加关注换乘和拥挤感受。

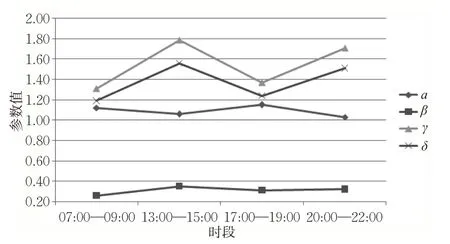
图2 式（1）中各参数的标定值Fig.2 Calculated values of each parameter in statement（1）

车内时间权重α 与换乘时间权重β，γ，δ 共同决定广义出行成本。同步调节参数α 与γ，研究不同时段下路径选择概率的变化情况。

如表3所示，对于直达路径，参数α 对结果的灵敏度更高，对于换乘路径，参数β，γ，δ 对结果的作用力更强。对于参数的变化，高峰期均比平峰期敏感。

在其它参数保持标定值的情况下，随着参数α由1.0 增加至2.0，直达路径在高峰期和平峰期的选择概率分别下降18.99%和13.94%，换乘路径选择比例相应上升。原因在于直达路径车内成本逐渐覆盖换乘因素，乘客自主选择拥挤度稍低的换乘方案，这在高峰期表现得更为明显。同理，随着参数γ 由1.0增加至2.0，换乘线路在高峰期和平峰期的选择概率分别下降8.44%和2.7%，直达路径选择比例相应增长。原因在于随着换乘复杂度的提升，拥挤度因素被换乘时耗逐渐代替，直达路径被更多人选择，这对通勤出行群体更具吸引力。

表3 工作日武汉市轨道“金银潭—江汉路”区间各路径依参数的选择概率演变Tab.3 Route assignment probability of“Jinyintan—Jianghan Road”section under different parameters on weekdays

3.2 客流指标获取

为进一步验证模型效用，需获取可测的量化指标，即根据标定的参数推演全网客流出行特征。而模型精度提高的同时也增大了运算规模，本文采用以下方法降低算法复杂度获取全网客流指标。

1）约束条件处理。调查结果显示1 次有效的轨道出行时间不超过120 min。本文按照30 min时间粒度，将全天（06：00—23：00）进站记录划分为34个(1 ≤i ≤34 )计算周期。比如在07：30—08：00时间段内进出“金银潭—江汉路”区间共计116 人次，基于闸机记录的出行时间平均值为27.4 min。以95%的样本覆盖率为目标，拟合该组闸机时间序列，获得有效闸机时间间隔min（见图3）。第i 个周期内，有效闸机时间用于约束路径的真实出行时间，排除非常规影响。

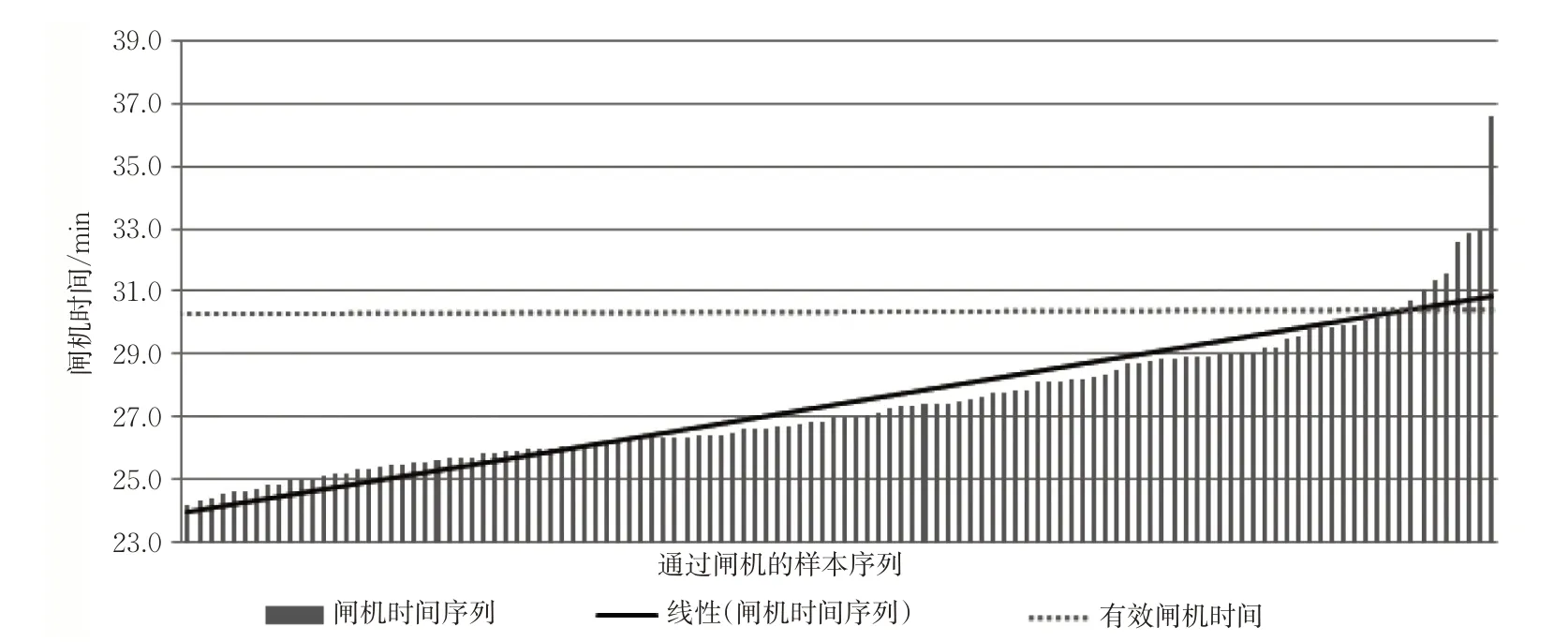
图3 工作日07∶30—08∶00武汉市轨道“金银潭—江汉路”区间乘客通过闸机时间序列Fig.3 Travel time series of“Jinyintan—Jianghan Road”section during 07∶30—08∶00 on weekdays

因此，某OD 的被选路径中第l 个断面（共计L个）在第i 个周期内的真实出行时间应满足

2）可行路径处理。网络结构方面，2019年上半年武汉市运营轨道线路9条，站点216座（见图4），对全网200 万余对站点OD 逐个搜索多路径需要大量运算资源。参考基于线路的拓扑转换方法[14]，本文将基于全网站点的断面集合转化为基于换乘站点的区间组合（见图5）。将换乘站点之间形成的换乘区间视为节点，换乘区间之间的联系视为邻接关系[15]，简化后的搜索规模压缩至54个换乘区间（双向）。除轨迹起终站点所在区间，换乘行为影响出行途经换乘区间所有断面的客流。

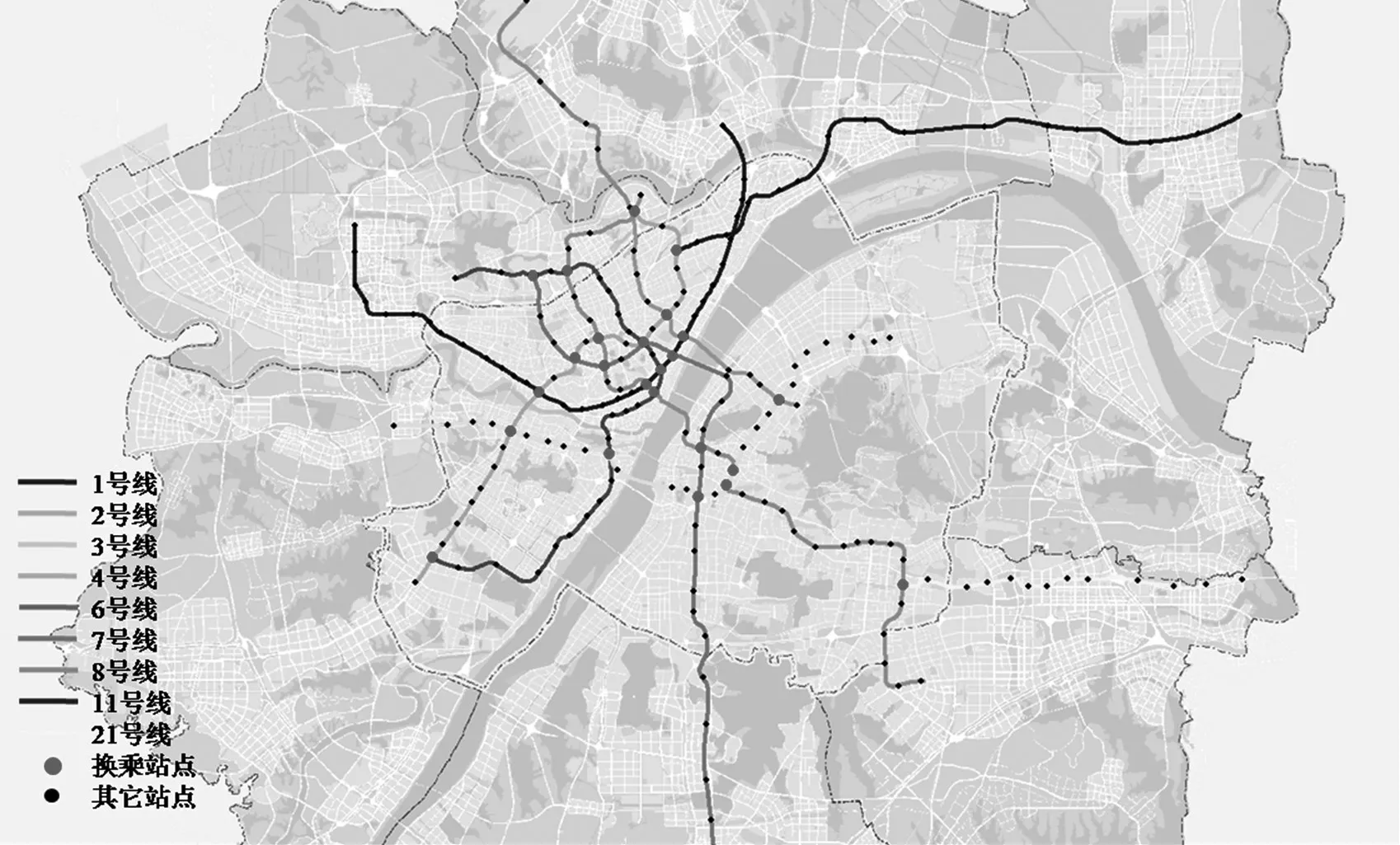
图4 基于传统线路站点的武汉市轨道网络拓扑结构Fig.4 Topological structure of Wuhan rail transit based on traditional lines and stations

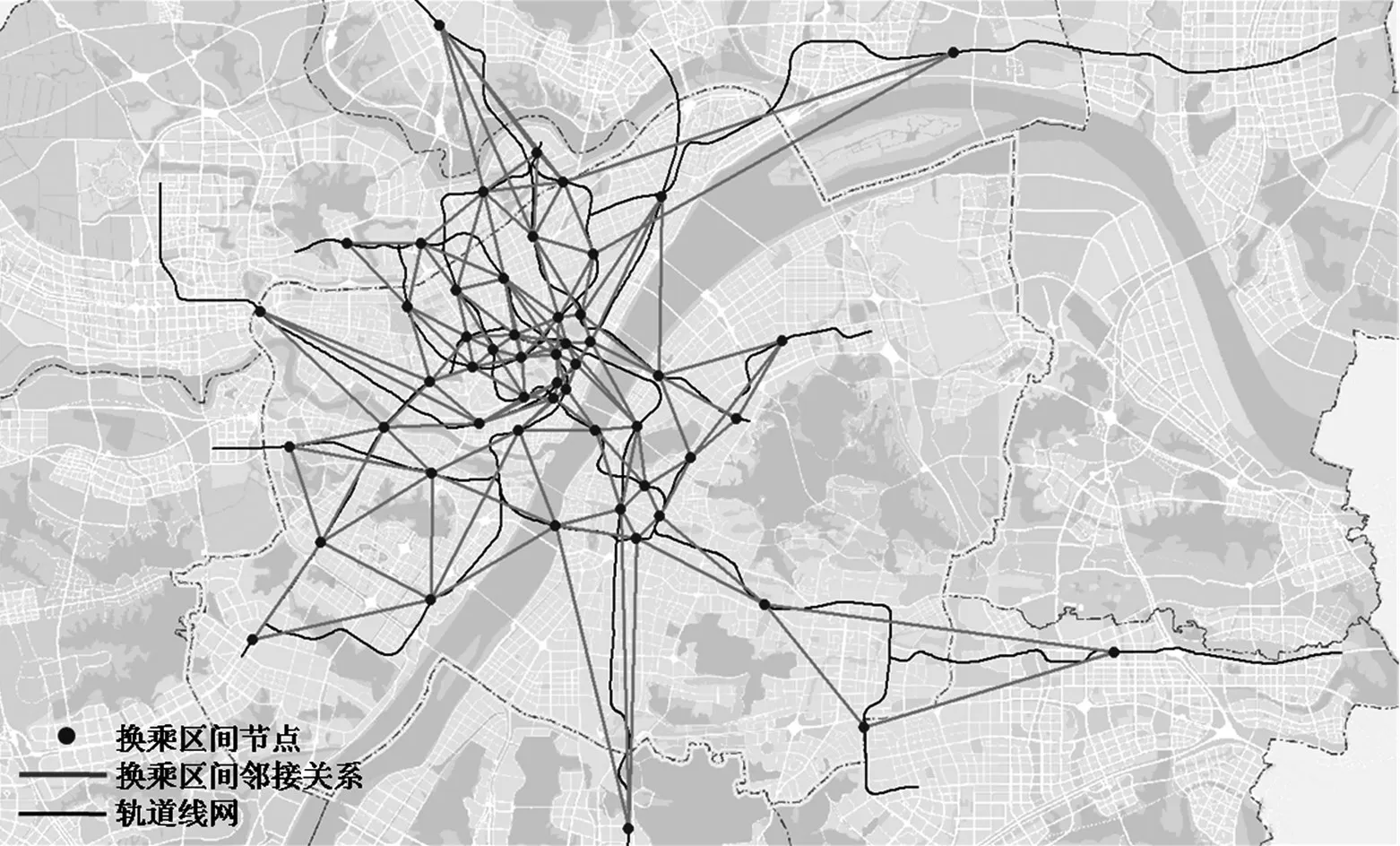
图5 基于换乘区间的武汉市轨道网络拓扑结构Fig.5 Topological structure of Wuhan rail transit based on transfer intervals

网络搜索方面，将标定有效闸机时间的站点OD 集合映射到简化拓扑结构中，参考多路径搜索算法[16]，基于广义出行成本计算每组出行组合的断面客流量与换乘站点客流量，具体步骤如下。

步骤1。建立简化的网络拓扑，每个轨道站点归属于某一换乘区间（换乘站进出情况在步骤3～4 中设计虚拟换乘[17]排除），重塑基于换乘区间的O′D′组合。

步骤2。针对某站点OD，按照实际起终站点均不是、其中之一是、以及二者都是换乘区间节点，分3种情况建立实际起终站点OD 与（见图4 中节点）与最近邻换乘区间节点O′D′（见图5 中节点）的几何关系。

步骤3。对于步骤2中的O′D′，在有效闸机时间式（5）的约束下，使用网络最短路法获取从起始区间节点O′到终止区间节点D′之间最小广义成本的路径轨迹，以及区间节点集合R1=[r1，r2，r3，…，rt-1，rt]。

步骤4。以R1作为首次迭代路径进行邻接修改处理，将[r1，r2] 权值设为∞，进行最短路搜索最小成本路径R11；再将[r2，r3] 权值设为∞，再次进行最短路搜索最小成本路径R12，迭代得到基于R1的广义成本集合[R11，R12，…，R1，t-1] ，取其最小成本与换乘区间集合R2。

步骤5。针对R2重复步骤4中操作达到搜索规模RK，迭代过程中Rk(1 ≤k ≤K) 若不满足式（5）则转向步骤8。

步骤6。结合式（4）计算该O′D′集合的K 条可行出行轨迹发生概率，依托换乘量与概率获得站点换乘客流量与基于换乘区间的断面客流量。

步骤7。根据步骤2 将该O′D′的起终节点还原到原始网络中，计算实际站点与换乘区间节点之间的断面客流量，形成该站点OD 的全部断面客流。

步骤8。操作下一OD，按照步骤2～7获得相应断面客流量与换乘站点客流量，重复至完成所有站点OD 集合遍历。

4 模型效验

通过上述模型标定方法与简化拓扑下的客流指标算法，可获得全网全天任意站点OD 的出行概率与出行量。本节选取全天、高峰和平峰的调查观测值，与计算结果对比，校核模型精度，同时在规划应用层面解析客流指标。

4.1 数值层面验证

对比调查结果和基于广义出行成本的路径选择概率，总体误差控制在5%以内（见表4）。2 类结果一致表明，断面客流拥挤与换乘次数对高峰期的刚性出行影响不大，通勤出行路径不会因车内拥挤或换乘复杂而改变，但平峰期给予自由出行者选择空间，对直达线路的选择比例更高。

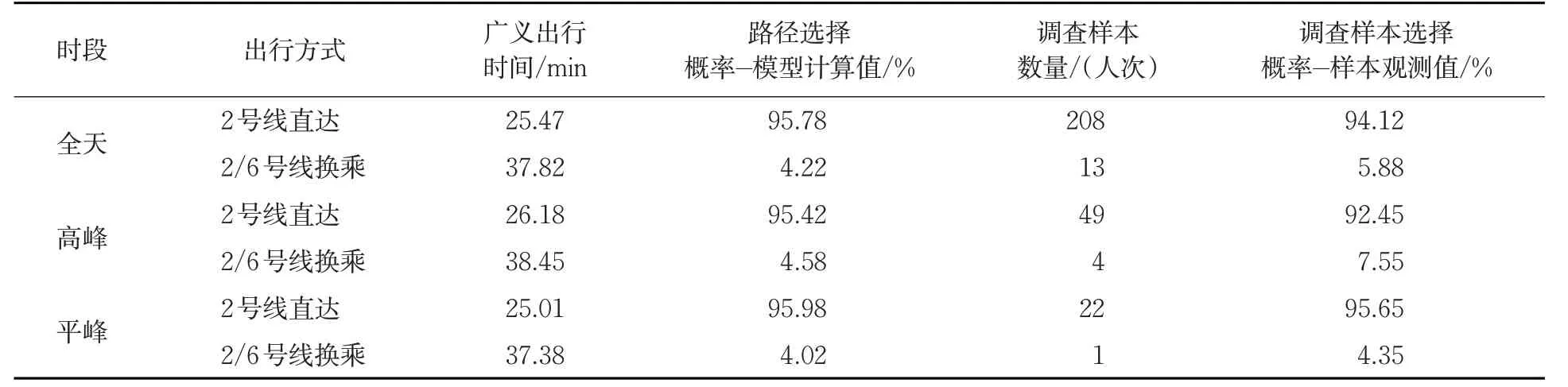
表4 工作日武汉市轨道“金银潭—江汉路”区间各路径选择概率与调查结果对比Tab.4 Comparison of calculated assignment probability and survey results of “Jinyintan—Jianghan Road”section during different periods on weekdays in Wuhan

4.2 规划层面解释

运用上述模型和数据，获得各换乘站点的换乘量值与分时特征。模型结果与现状客流运行时空特征一致。空间分布上，换乘站点主要设置在主城核心区内，且临近过江通道的站点换乘量级更高（见图6）。比如长江通道上的循礼门站（1/2号线换乘站），汉江通道上的王家湾站（3/4 号线换乘站）。时间分布上，早晚高峰小时的平均换乘比例分别为11.8%和10.2%，通勤通学群体是换乘的主体。

另一方面，模型结果描述了换乘特征与公交一体化发展战略的相关性。在东风公司等岗位聚集地，其就业人口的居住分布地较为广泛，高峰期站点换乘比例超过50%。而在常青花园等居住聚集地，其居住人口的就业地更趋向于集中在若干区域，高峰期站点换乘比例不到30%。上述特征是中心城区轨道线网加密、常规公交线网接驳、远城区轨道线网延伸等规划方案的重要支撑。

5 结束语

本文以武汉市轨道系统为案例，结合动静态数据，建立了一套时变网络结构下的路径动态选择模型，应用于站点与断面客流特征分析与规划设计，具体如下。

1）以乘客出行需求与运营时刻表为基础构建时变的网络拓扑，将轨道站点视为网络节点，站间出行时间视为节点联系，按照进站时间将全网客流划分为若干子集合，每个子集合运行于不同的网络载体，并作用于其后若干连续子集合。

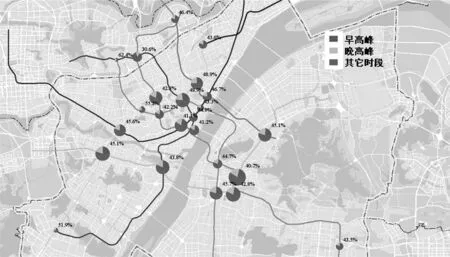
图6 工作日武汉市轨道换乘站点不同时段客流换乘比例情况Fig.6 Passenger flow of transfer stations during different periods on weekdays in Wuhan

2）研究影响路径选择的因素形成广义出行成本与效用函数，考虑个体进出站行为对网络整体满载情况的影响，在概率空间中独立处理个体出行，整体研究出行群体的相互作用，强调任何个体行为都是整体特征不可忽略的一部分，但并不提前做出分类标记。

3）将基于轨道站点的网络结构映射为基于换乘区间的拓扑结构，重塑出行OD，并引入有效时间作为路径可行性判别依据，建立基于换乘区间网络的客流指标获取算法，降低运算规模以满足工程可行性要求。

上述路径动态选择模型考虑了出行供需关系的演化过程，相比于物理最短路径分配方法，通过时变拓扑模拟了网络运行环境，相比于基于运营时刻表的分配方法，通过时变满载率描述了出行心理感受。案例仿真说明模型精度达到预期要求，能科学引导线网规划、强化服务盲区、支撑换乘通道与站台容量设计等。

同时，除时间范畴的影响因素外，乘车条件（比如武汉轨道1 号线是轻轨，需面对夏季室外高温），站外接驳便利性[18]，及乘客对线网的熟悉程度等也是影响路径选择的重要条件，后续研究中将更为细致地模拟轨道客流换乘行为。