基于蒙特卡洛方法的飞机襟翼不对称风险预测*

马 超 张雄飞 徐建新

（中国民航大学航空工程学院 天津300300）

0 引 言

飞机的操纵系统是飞机的核心系统之一，飞行员通过操纵系统来实现安全飞行任务，保证飞机处于正常的飞行姿态[1-2]。飞机襟缝翼故障问题可能是由传动及支撑元构件失效、运动副磨损、传动机构失效等因素引起的襟缝翼卡阻等原因导致[3-4]。2014—2019年间，波音737NG系列飞机发生的重大故障统计中，飞机操纵系统占有较高的比重。因此，对飞机操纵系统状态监控及故障预测成为保障飞行安全的重要内容。

国内外学者先后对飞机操纵系统进行了研究，J.Rea[5]通过波音777 升力控制系统HLCS（High Lift Control System），研究了关于前缘襟翼和后缘襟翼驱动及执行系统的控制原理；Anderson等[6]提出了一种成功评估未来高性能飞机控制系统方法，将多种建模和分析技术集成到一种评估方法中；程科[7]通过对飞行数据的分析及数据特征值的提取，开展了基于QAR 数据的故障时间预测方法对后缘襟翼不对称故障进行研究和预测；朱晓炜等[8]通过解析报文数据结合后缘不对称工作原理，针对737NG 开发了关于后缘襟翼监控项目，基本实现预判故障状态；吴帧涛等[9]基于飞行数据对飞机操纵系统提出了故障评估方法。目前，飞机故障诊断方法和技术虽然获得了一定的成果，但对于飞行操纵操纵系统故障诊断方法研究不够充分，关于飞机QAR数据的有用信息利用率较低，无法发挥该数据应有的内含价值，很多研究未能结合工程实际需求或应用。

蒙特卡洛（Monte Carlo）模拟属于概率分析法，是一种采用已知概率分布，通过生成合适的随机数来预测各种不确定因素发生变化时对所研究目标评价指标的统计方法。其基本思想是如果所要求解的问题是某个随机变量的期望值或某种事件发生的概率，则可以通过相应地试验方法获取此随机变量的平均值或该事件出现的频率，以此作为所要研究问题的解[10-11]。赵洪利等[12]基于蒙特卡洛方法对民用航空发动机做了故障风险预测；常书丽等[13]利用蒙特卡洛方法，在大量试验数据的基础上，对燃气式发射装置内弹参数的随机分布进行了研究。

为了更好地监控飞机襟翼不对称故障，航空公司一般会根据飞机飞行时后缘襟翼左右角度差值来设定阈值，本文调研的航空公司，该阈值设置为当该差值大于等于3°时，就会进行故障报告。但实际情况发现，在所有大于3°的警报当中，有很大一部分属于无效警报，在进行检修时并未发现故障，这给航空公司增加了不必要的维修工作。因此，本文使用蒙特卡洛模拟方法，较好地解决样本数据缺乏问题，形成大样本数据，深入挖掘襟翼不对称超限事件的后缘襟翼角度数据，对飞机襟翼不对称的风险进行分析与准确预测。

1 飞机襟翼不对称故障

襟翼不对称是指襟翼左侧与右侧在收放时角度不一致，根据AMM（Aircraft Maintenance Manual）手册规定，当后缘襟翼左右角度差值大于9°时称为后缘襟翼不对称故障。波音公司发布的737 NG飞机襟翼不对称问题的说明中指出其主要原因是襟翼指示器故障和襟翼位置传感器故障。飞机左右襟翼位置分别由位置传感器来提供数据，襟缝翼电子组件（Flaps/Slats Electronic Unit）接收来自传感器的信号。因此，通过后缘襟翼传感器所记录QAR数据的角度差值便可对后缘襟翼不对称问题进行监控。快速存储记录器（Quick Access Recorder, QAR）数据记录飞机真实飞行状态的各种参数，可以同时对1 000 多种数据进行采集，是航空公司进行飞行品质监控、发动机性能监控、飞机维修排故辅助等工作的重要参考依据[14]。在实际监控中发现，角度超差频出主要发生在飞机稳态飞行中。稳态定义为如果襟翼角度变化与上一秒变化在1°以内，便认为是稳定转态；如果襟翼角度与上一秒变化在1°之外，便认为襟翼处于作动状态。襟翼的过快或者过慢收放都会导致襟翼不对称故障问题。

在一个飞行循环中，后缘襟翼操作停留时间较长的档位依次是UP 档、5 档和30 档，处于这些档位时样本数据比较充足。当襟翼档位进行变换时，襟翼角度值随之变化。通过对数据进行非稳态剔除，得到稳态数据进而分析。

根据AMM 手册，当后缘襟翼左右角度差大于9°时，0.5 s后会触发襟翼旁通活门，大于9°状态持续3 s后，襟翼旁通活门锁定，襟翼在空中便无法继续操控，只有在地面才可进行复位。所以，为避免不安全事件的发生，目前一些航空公司监控的阈值为3°，超过3°系统会有报警提示。以B 737-800飞机为例，对正常飞机B1与故障飞机B2的QAR数据进行稳定状态后缘襟翼左右角度作差，结果见图1～2。

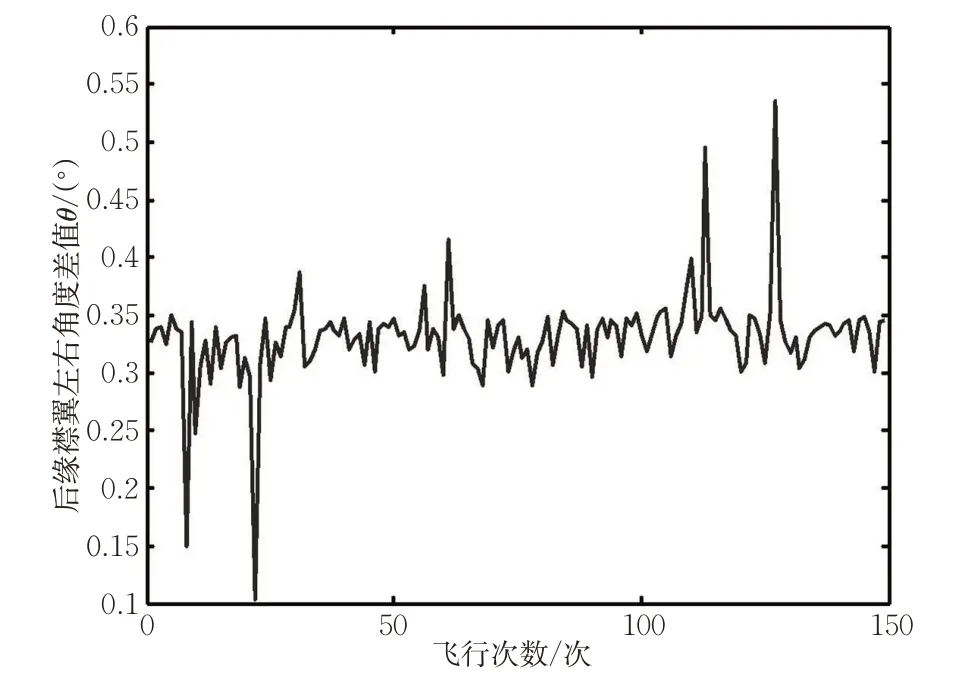
图1 B1稳定状态后缘襟翼左右角度差值Fig.1 B1 of left-right angle difference of trailing-edge flap in stable condition

图2 B2稳定状态后缘襟翼左右角度差值Fig.2 B2 of left-right angle difference of trailing-edge flap in stable condition

由图2可知，在227次航班处（最高点）发生了襟翼不对称故障。统计发现在故障发生前，左右后缘襟翼角度差值波动在1.5～4.5°之间，在对故障排查维修后，波动值突然下降为0～2.5°之间，说明QAR数据能够直观反映故障特征。因此，本文通过研究故障发生前3 个月的后缘襟翼左右角度差值数据，使用蒙特卡洛方法建立了襟翼不对称风险值模型。

2 飞机襟翼不对称故障风险预测算法

2.1 建立襟翼不对称风险评价模型

风险是指在某一特定环境下，某一段时间段或周期内，某种损失发生的可能性及主体受损失程度的叠加[15-16]。因此，可由某种损失事件发生的概率及其后果的严重程度函数表示。飞机襟翼不对称风险评价模型用襟翼不对称发生的概率与襟翼发生后导致的后果严重程度二者乘积来表示，即

式中：VPX为飞机后缘襟翼发生不对称事件的风险值；PPX为后缘襟翼发生不对称事件的概率；SPX为后缘襟翼不对称事件发生后的严重程度。

2.2 随机变量的抽样模拟

1）构造概率过程。通过对大量飞行数据研究发现，在较大的数据样本空间（N＞100）里，大部分飞行性能参数都近似的呈正态分布规律[15]。在已知概率分布的基础上，应用蒙特卡洛模拟方法得到关于后缘襟翼左右角度差值随机度数的正态分布，通过此方法生成的随机数能够很好的满足实际问题需求，并且具备分布均匀性、独立性及随机性。

2）抽样模拟方法。抽样采用Box-Muller变换算法[17]，用已知服从正态分布的样本数据进行Box-Muller变换，可得所需随机序列，变换公式见式（2）。

式中：α 为飞机后缘襟翼左右角度差值的随机度数；r 和t 为独立随机数，该数值满足在( 0，1) 值域内服从均匀分布；μ 和σ 分别为已知样本数据（符合正态分布）的均值和标准差。

2.3 风险值计算过程

1）计算均值和方差。

式中：Xi为原始样本数据的数值；μ 为原始样本数据的均值；n1为原始样本数据的个数；n2为经过Box-Muller 变换所得随机数个数；αi为经过Box-Muller 变换所生成的随机数；αˉ为生成随机数的均值；分别为原始样本数据和生成随机数的方差。

2）假设该样本数据符合N( μ，σ2)正态分布，需要进行正态分布检验，若其结果表明样本数据符合正态分布，则对其方差进行修正，得到总体方差进行无偏估计

3）综上可得，该机型后缘襟翼左右角度差值的分布函数为

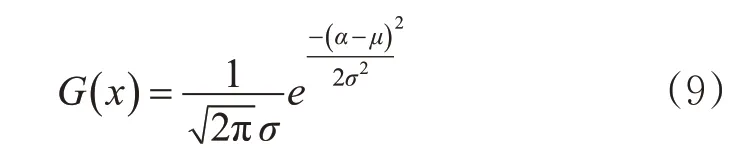
从式（9）可知，后缘襟翼不对称事件发生的概率与α 靠近期望值的差值成正比，使用蒙特卡洛模拟方法对飞机后缘襟翼左右角度差值样本进行扩充，应用式（1）对襟翼不对称风险值进行计算，其中PPX的计算公式见式（10）。

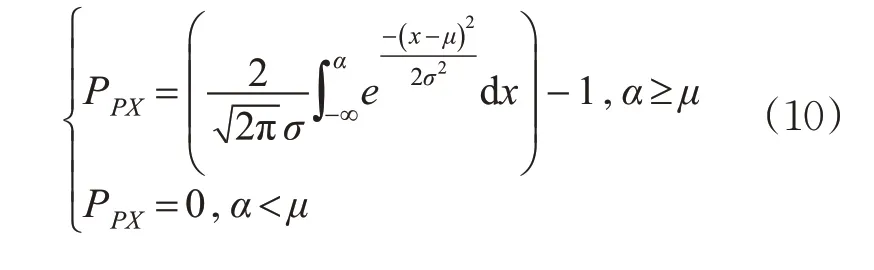
本模型以样本数据偏离均值的程度来表征后缘襟翼不对称事件发生后的严重度，因此，偏离值越大则代表着该事件的严重程度越高，其计算公式见式（11）（SPX≥0）。

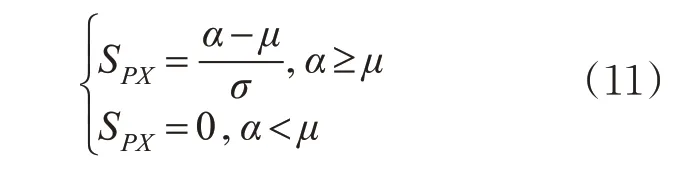
2.4 襟翼不对称风险值的评估与预测

经过Box-Muller 方法的变换，得到了在一定范围内的飞机后缘襟翼左右角度差值随机度数α，应用风险预测模型VPX=PPX*SPX，则飞机襟翼不对称风险预测值的表达式可表示为

式中：r 和t 分别为服从( 0，1) 正态分布中相互独立的随机数；μ 和σ 分别为已知样本数据的均值与标准差。

2.5 风险等级定量划分

由式（10）定义可知PPX取值范围在( 0，1) 之间，由正态分布3 σ 准则可知，99%以上的数据分布在区间( μ-3σ，μ+3σ )内，因此结合式（11）定义可得SPX相应大部分的取值范围为( 0，3) ，故根据式（12）可知后缘襟翼不对称风险取值范围为( 0，∞)，综上，可将后缘襟翼不对成风险等级作如下划分，见表1。

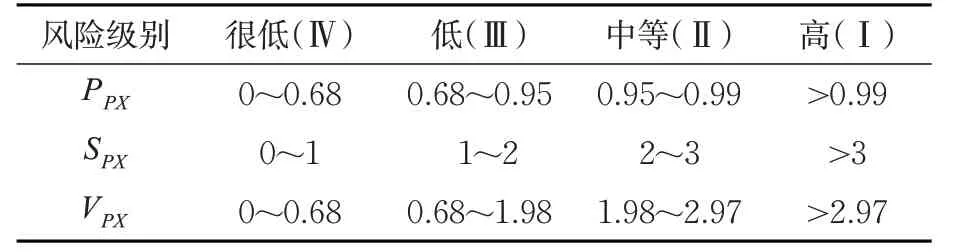
表1 后缘襟翼不对称风险等级划分Table.1 Asymmetric risk classification of trailing-edge flap

依据VPX取值范围，可将后缘襟翼不对称风险等级划分为四个等级，由低到高分别为Ⅳ～Ⅰ级别。

2.6 蒙特卡洛模拟流程

通过上述预测模型，利用Matlab编程进行8 000次抽样模拟试验，可得到8 000 个飞机后缘襟翼不对称风险预测值。蒙特卡洛模拟流程见图3。

取( 0，1) 分布上相互独立的2 个随机数r 和t ，可计算出后缘襟翼左右角度差值α1；由式（10）～（12），便可得到VPX，完成1次抽样。同理，将此过程进行8 000次抽样，便可得到8 000个后缘襟翼不对称风险值V1，V2，…，V8000。以后缘襟翼左右角度差值为横坐标，后缘襟翼不对称风险值为纵坐标，可得后缘襟翼不对称风险预测曲线。

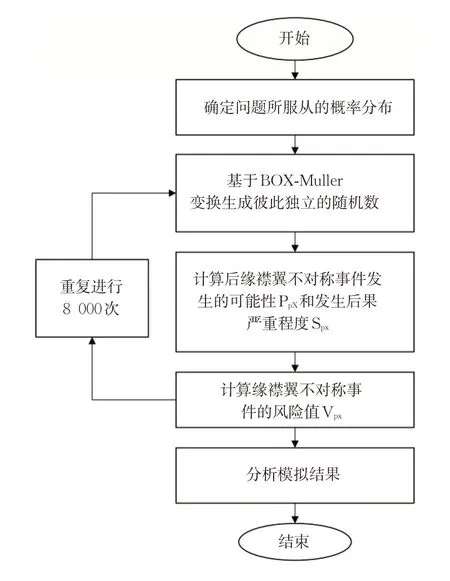
图3 蒙特卡洛模拟流程图Fig.3 The flow diagram of Monte Carlo

3 实例分析及模型验证

本文使用的样本数据为某航空公B737-800机型的飞行QAR数据，其中飞机A于2019年5月26日发生后缘襟翼不对称故障，取其故障发生前3个月的飞行QAR数据316组；飞机B于2019年6月21日发生后缘襟翼不对称故障，取其故障发生前3 个月的飞行QAR数据400组，通过Matlab编程处理该样本数据，得到2架飞机在稳态时的后缘襟翼左右角度差值频率直方图及后缘襟翼左右角度差值分布图，见图4～7。

图4 飞机A后缘襟翼左右角度差值的频率分布Fig.4 The frequency distribution of left-right angle difference of trailing-edge flap of aircraft A

图5 飞机A后缘襟翼左右角度差值分布Fig.5 The distribution of left-right angle difference of trailing-edge flap of aircraft A

图6 飞机B后缘襟翼左右角度差值的频率分布Fig.6 The frequency distribution of left-right angle difference of trailing-edge flap of aircraft B

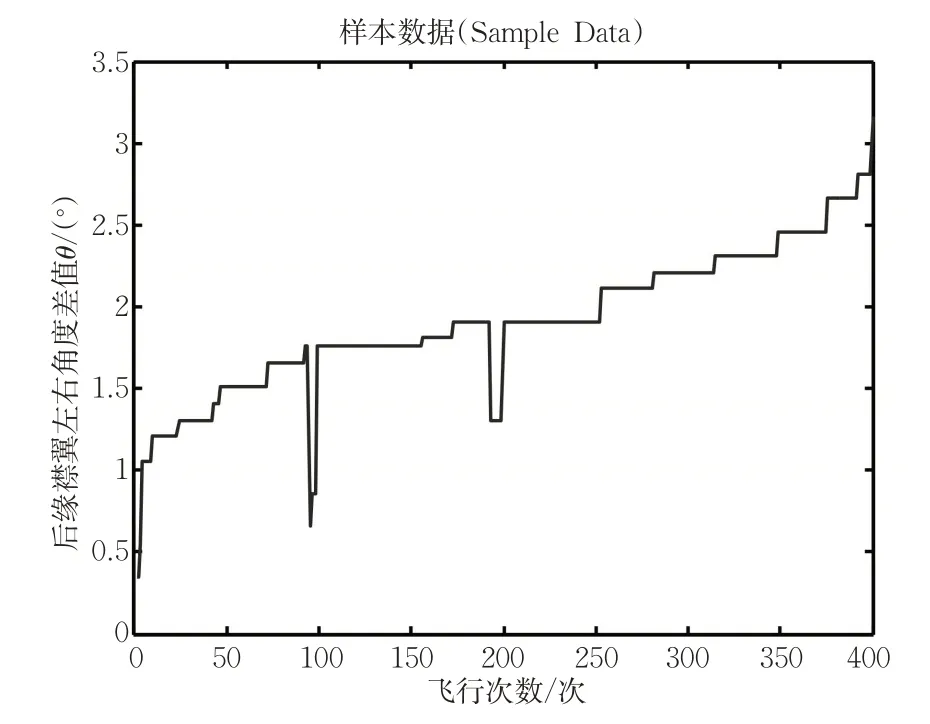
图7 飞机B后缘襟翼左右角度差值分布Fig.7 The distribution of left-right angle difference of trailing-edge flap of aircraft B

由图4可知，飞机A后缘襟翼左右角度差值均值为3.625 7，标准差为0.201 7。

由图6 可知，飞机B 后缘襟翼左右角度差值均值为1.900 5，标准差为0.438 6。

从差值分布图5及图7可以发现，飞机在发生襟翼不对称故障前数据有2 种变化转态，一种为波动型，即在某一水平线上作上下波动；另一种为递增型，即数据总体呈递增的状态增长。

利用Box-Muller 变化随机生成8 000 个后缘襟翼左右角度差值数，得到飞机A 和飞机B 的后缘襟翼左右角度差值频率分布直方图，见图8～9。

图8 飞机A随机生成的后缘襟翼左右角度差值频率分布Fig.8 The frequency distribution of left-right angle difference of trailing-edge flap generated randomly of aircraft A

图9 飞机B随机生成的后缘襟翼左右角度差值频率分布Fig.9 The frequency distribution of left-right angle difference of trailing-edge flap generated randomly of aircraft B

通过后缘襟翼左右角度差值抽样模拟结果与样本数据对比，飞机A标准差由0.201 7变为0.110 5，飞机B 标准差由0.438 6 变为0.424 1，数据质量得到了一定的提高。

采用统计大样本容量数据较好的Jarque-Bera（J-B）检验[18]，检验结果得知样本符合正态分布。通过式（1）可以对蒙特卡洛法所生成随机数的后缘襟翼风险值进行计算，得出了飞机A 和飞机B 后缘襟翼左右角度不同差值所对应的风险值的预测曲线，见图10。

图10 飞机A和飞机B后缘襟翼不对称风险预测曲线Fig.10 The risk prediction curve of asymmetric trailing-edge flap of aircraft A and aircraft B

图10 是对飞机A 和飞机B 后缘襟翼不对称风险进行模拟8 000 次后的结果，从图中可以看出，2架飞机风险预测曲线有所不同，飞机A 后缘襟翼左右角度差值为3.626度时风险值开始增长；飞机B后缘襟翼左右角度差值为1.900度时风险值开始增长，且飞机A的增长斜率明显大于飞机B。这是由于每架飞机出厂情况与后期使用过程中的维护和保养情况差异，使得每架飞机具有各自的襟翼不对称风险阈值。通过监控飞机的风险值，可以更加高效、快捷的预测飞机发生后缘襟翼不对称故障发生的可能性。飞机A和飞机B后缘襟翼左右角度差值与风险级别关系统计结果见表2和表3。

表2 飞机A 后缘襟翼左右角度差值与风险级别关系Table.2 The relationship between left-right angle difference of trailing-edge flap and risk level of aircraft A

表3 飞机B 后缘襟翼左右角度差值与风险级别关系Table.3 The relationship between left-right angle difference of trailing-edge flap and risk level of aircraft B

从上表中可以看出，飞机A风险级别为Ⅰ时，对应的后缘襟翼左右角度差范围为：4.23～4.38；而飞机B 风险级别为Ⅰ时，对应的后缘襟翼左右角度差范围为：3.19～3.56。这表明，对于相同风险等级的情况，不同飞机后缘襟翼左右角度差范围存在差异。

为了对后缘襟翼不对称风险模型进行验证，选取A/B 飞机发生故障时的前3个月数据和后1个月数据，分别为353 组与389 组数据，得到飞机A/B的运行状态监测图，见图11～12。

图11 A飞机运行状态监测Fig.11 Operational condition monitoring of aircraft A

由图11可知，A于点219处发生故障，故障前有16个点位于Ⅲ～Ⅳ级别，2个点位于Ⅱ～Ⅲ级别，0个点位于Ⅰ～Ⅱ，故障经维修后，后缘襟翼左右角度差均在Ⅳ级别以下。同样情况，从图12 可知，B 于点334处发生故障，故障前有58个点位于Ⅲ～Ⅳ级别，2个点位于Ⅱ～Ⅲ级别，0个点位于Ⅰ～Ⅱ级别，2个点位于Ⅰ级别以上，故障维修后，所有的点均落在Ⅳ级别以下。

综上可知，通过设计合理的风险级别，可以有效地实现飞机后缘襟翼的监控，后缘襟翼发生故障之前，存在监控值风险级别升高的故障征兆。另外，根据不同飞机的实际情况，风险级别的划分要依据长期积累的飞机QAR数据进行制定，这样才能更加有效的实现飞机的监控与风险预测。

图12 B飞机运行状态监测Fig.12 Operational condition monitoring of aircraft B

4 结束语

1）笔者以航空公司真实飞机QAR 运行数据作为研究对象，基于飞机襟翼工作与监控原理，利用蒙特卡洛方法对飞机在稳定状态下后缘襟翼监控数据进行了模拟抽样试验，解决了故障样本量不足的问题，同时，样本标准差也得到了有效地提高。

2）提出了飞机后缘襟翼不对称风险级别的概念，定量划分了襟翼不对称风险等级，研究发现不同飞机在相同后缘襟翼不对称风险值情况下所对应的后缘襟翼左右角度差不同。基于飞行QAR数据，对不同飞机监控阈值进行差异化设计有助于提高后缘襟翼不对称故障的监控效率。