高速公路施工区自动车辆行驶轨迹优化方法*

李晓虎 麦 乐 任 杰 刘浩学 朱 彤

（长安大学汽车学院 西安710064）

0 引 言

高速公路施工区是高速公路经常发生交通事故和交通效率下降的路段[1]。研究发现，驾驶人在进入施工区为了提高自身的运行速度会采取不同的换道方式，不规则的换道过程会使不同车辆之间的运行状态受到严重干扰[2]。为了改善高速公路瓶颈路段现存问题并发挥现有高速公路交通设施的最大效益，部分学者提出了主动交通管理(active traffic management,ATM)，其中包括匝道控制和可变限速等措施。如Jin等[3]提出了在瓶颈路段上游通过设定可变限速控制以减少瓶颈路段车辆密度和增加车辆之间行驶间隙，以此缓解瓶颈路段车辆之间换道干扰，提高交通效率。Scarinci 等[4]搭建Matlab-Vissim 仿真平台，提出了一种新的匝道控制措施，即基于匝道控制中在匝道口处安放信号灯的方法，通过检测器检测高速公路主线上的车辆之间的间距是否大于预设的汇入间隙以此来控制信号灯的周期，使得车辆能够在不影响主路旅行时间的情况下安全汇入，显著减少了瓶颈区域内的交通冲突。

近年来，随着网联自动车(connected and autonomous vehicle，CAV)技术的发展[5-6]，直接对每辆车运行状态调节，以此改善微观交通流特性。如Ali等[7]通过驾驶模拟器研究高速公路上网联自动车环境在车辆强制换道过程对中安全性的影响，通过分析模型中的生存率和危险率等指标，得到了网联自动车环境在强制换道操作期间可以较大的提高安全性。Gong 等[8]基于车辆与车辆之间的“通信”为改善换道过程提出建议，使得车辆能够在适当的位置进行平稳的强制性换道。Park 等[9]通过实验数据拟合得到速度和加速度曲线，通过仿真为汇入车辆制造出一个动态换道间隙，该动态间隙能够显著的提高交通效率与减少冲突。张新锋等[10]从智能车本身出发，利用多项式函数进行换道轨迹规划，建立了基于稳态转向特性和安全距离的换道模型，利用Matlab 与CarSim 软件进行仿真分析，结果表明，其方法能够实现智能车辆的自动换道行为并且控制效果较为理想。兰凤崇等[11]通过考虑车辆操纵稳定性建立了车辆三自由度模型，对轨迹综合优化目标函数进行求解，得到了在不同车速情况下智能车最优换道行驶轨迹。张琳等[12]在研究车辆动力学模型特性的基础上，考虑车辆自身约束提出了一种动态轨迹规划方法，通过最优指标决策出最优轨迹和车速，并验证了方法的有效性。

综上，以往研究较少的考虑结合交通流分布和车辆运行状态参数的改变对施工区处车辆行车轨迹进行优化。笔者通过结合高速公路环境信息，建立了交通流分配模型和可变跟车时距模型，以在线的方式对施工区上游进行换道比例计算和汇入路段可变跟车时距优化，并以车辆行驶轨迹、速度标准差等作为表现形式，对施工区车辆运行状态进行可视化分析。

1 换道控制策略

在临近施工区处往往会因过多车辆需要强制换道而导致安全性和交通效率下降，见图1（a）。结合交通流分配和施工区车辆安全汇入思想[13]，所提出的换道控制策略分为：①在施工区上游对车辆进行交通流分配，此时借助遗传算法通过遍历交通流状态并结合路边检测器识别是否存有换道冲突车辆对目标函数进行求解，以此得到区间换道比例，减少施工区封闭路段车辆的换道压力。②在施工区汇入部分对主线车辆进行可变跟车时距计算，通过求解所设定的目标函数，在线计算与反馈可变跟车时距，在保证主线车辆行驶稳定的情况下，为汇入车辆制造出汇入间隙，确保全局车辆行驶轨迹连续平稳，见图1（b）。

1.1 交通流分配模型

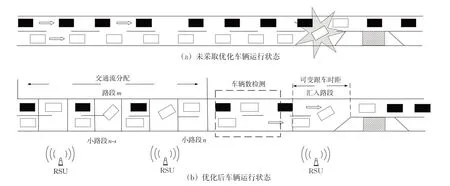
图1 车辆运行状态比较Fig.1 Comparison of vehicle driving status

为减少施工区汇入部分因强制换道车辆数较多而导致外车道车辆堆积和交通效率下降现象。提出了在施工区上游对交通流进行提前分配模型。即在施工区上游长度为L 的路段m 设定为交通流分配区域，将路段m 划分为n 个小路段，每个小路段旁设有路边检测器单元（road side units，RSU）进行换道冲突识别，每个小路段交通流分配方式见图1（b）。在所提出的交通流分配理论中，外车道车辆在接收到“指令”分配到内车道时，此过程会导致外车道车辆为了换道而减速，内车道车辆因外车道车辆汇入和道路密度的增多而行驶缓慢。为了不因交通流分配而导致交通效率降低，以内外车道车辆在总仿真时长内平均速度为目标函数，对施工区上游车辆进行交通流分配。此时交通流分配目标函数见式（1）。

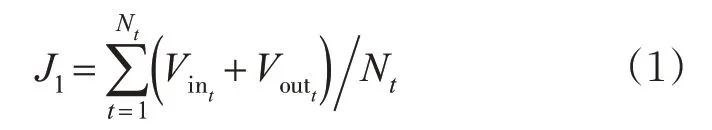
式中：t 为单位仿真步长，s；Nt为总仿真时长，s；Vint为单位仿真步长内施工区上游内车道车辆运行速度，m/s；Voutt为单位仿真时长内施工区上游外车道车辆运行速度，m/s。

对目标函数式（1）设置的控制变量为每个小路段的换道比例，即每个小路段的换道比例在0～1 之间选取[14]。其控制变量限制见式（2）。

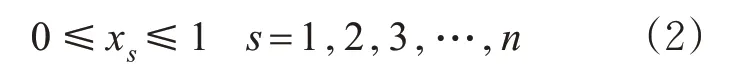
式中：s 为不同小路段；xs为每个小路段的换道比例。

在换道过程中，一个安全换道间隙能够保证车辆安全平顺的换道至目标车道[15]。为了不因过多的交通流分配导致冲突数上升，每个小路段中车辆换道时，目标车道上的车辆间距需要满足最小安全距离，当换道间隙过小时，车辆继续行驶至下一小路段，此时需要考虑的条件见式（3）～（4）。

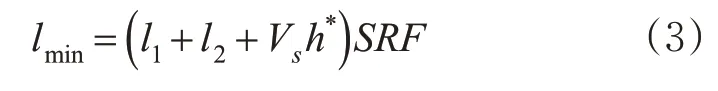
式中：lmin为车辆换道过程中需要满足的最小安全间距，m；l1为目标车道上前车的长度，m；l2为车辆静止时的最小安全距离，m；Vs为自由流下每个小路段s 的车辆平均速度，m/s；h*为驾驶员想要保持的最小跟车时距，s；SRF 为安全距离折减系数，表示驾驶员在换道过程中冒险行为参数；l 为目标车道上车辆行驶间距，m。

1.2 可变跟车时距模型

为优化施工区处车辆行驶速度和交通冲突，提出了在施工区汇入部分的可变跟车时距模型。因施工区处为车道减少路段，其中存在因车辆强制汇入导致局部车辆行驶缓慢和冲突。对此，结合施工区汇入部分的车辆运行速度和冲突风险为目标函数，得出不同时间段的主线车辆跟车时距，以此在不影响交通效率下避免交通冲突。研究表明，车辆的速度离散性与冲突风险之间存有相关关系，即速度离散性越大表示冲突风险越大[16]。以速度离散性表示冲突风险，速度离散性的表示形式为每个时间步长不同车辆之间的速度差，此时可变跟车时距模型中目标函数具体表达形式见式（5）。

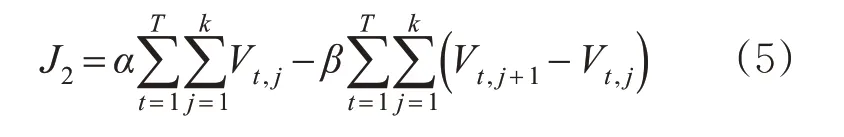
式中：T 为优化间隔，s；j 为车辆编号；k 为优化间隔内收集到的车辆总数；α，β 为速度与冲突风险之间的权重关系[17]；Vt，j为在第t 个仿真步长下第j 辆车的速度，m/s。

考虑到施工区处的速度限制，施工区处每辆车速度不能超过施工区限速值Vlim，m/s，即

考虑到高速公路的乘客舒适性，对加速度进行以下限制，见式（7）～（8）。

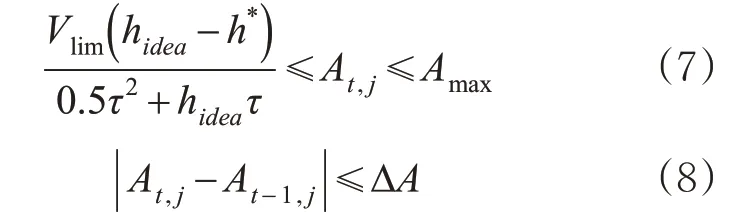
式中：hidea为期望跟车时距，s；τ 为车辆在自由流下通过汇入路段的时间，t；At，j为在第t 个仿真步长下第j 辆车的加速度，m/s2；Amax和ΔA 分别为加速度和加速度差值的允许限制，m/s2。

相邻仿真步长内车辆行驶距离、速度、加速度和时间之间的关系计算见式（9）～（10）。

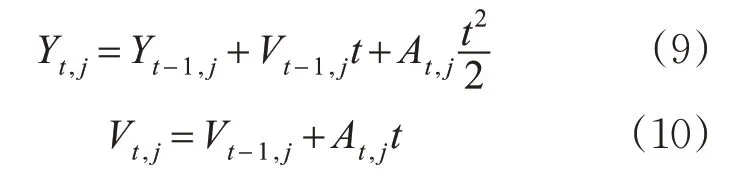
式中：Yt，j为在第t 个仿真步长下第j 辆车的行驶距离，m。

在不影响主路车辆行驶下，为汇入车辆制造出足够的间隙以此提高车辆汇入数量，此时车辆最小跟车时距限制见式（11）。

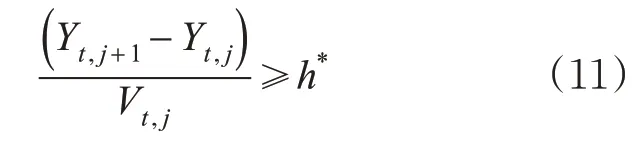
在计算过程中，为了减少冲突风险带来的影响，需要设置以下约束。

1）每个时间步长内相邻车辆间的速度差应小于ΔV1，m/s。

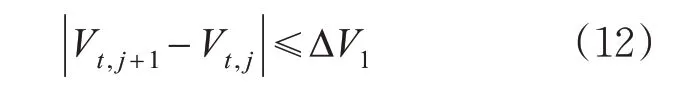
2）相邻时间步长内的速度差值应小于ΔV2，m/s。

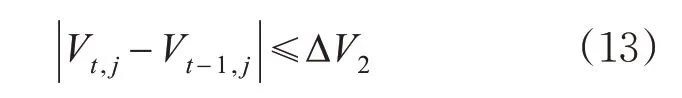
1.3 目标函数求解

1.3.1 交通流分配模型求解

交通流分配模型中车辆换道过程可视为0-1 问题，即比较在不同小路段内车辆是否换道求取目标函数最优解，此时借助遗传算法对交通流分配模型求解。所设定的遗传算法的种群规模为20，种群代数为20，交叉概率为0.7，变异概率为0.05。由于待求解的目标函数中速度与小路段换道比例并没有直观的公式表达，此时需要通过遗传算法联合外部仿真软件进行求解。以内外车道车辆在总仿真时长内平均速度J1的负数为适应度函数，借助仿真软件遍历不同换道区间的换道比例，求解适应度函数达到最小值时的控制变量取值。

1.3.2 可变跟车时距模型求解

以CPLEX 应用程序编程接口(Application Programming Interface，API)在Matlab中编辑与求解可变跟车时距模型目标函数J2的最大值。由于单纯的使用CPLEX通过API在Matlab中编辑函数复杂性较高，因此通过Matlab中Yalmip优化工具箱进行函数的编辑，然后通过Matlab调用CPLEX的API接口，使得目标函数在CPLEX Database环境中求解。

2 仿真实验设计

2.1 实时反馈模拟环境

为了实现网联自动车环境，利用Matlab 通过COM 接口与Vissim 联合仿真。通过Matlab 提取Vissim中数据并进行计算得到优化控制，通过COM组件将数据实时反馈给Vissim进行可视化。具体思想为建立Vissim_COM 与Matlab 的交互界面，在Matlab中获取换道比例和跟车时距等控制优化值并返回至交互界面，通过COM 接口将所得优化值在Vissim中进行设定，其环境结构见图2。

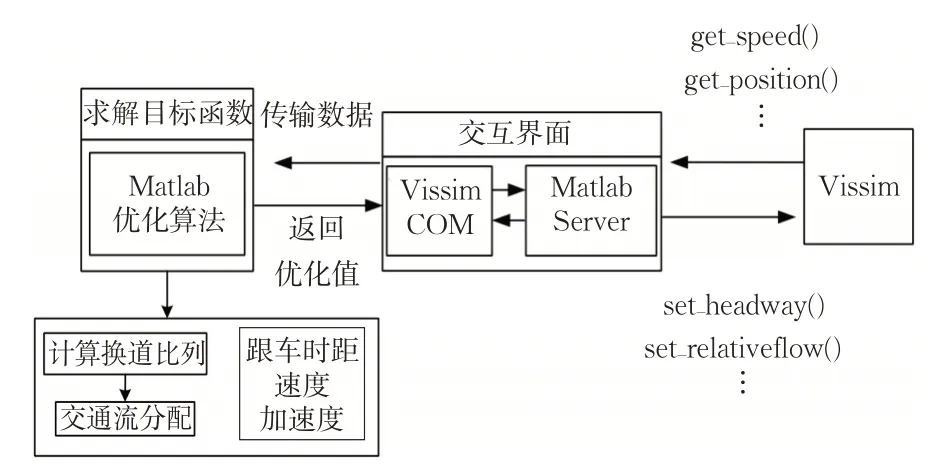
图2 模拟环境结构图Fig.2 Simulation environment structure diagram

2.2 交互规则

在每次仿真交互过程中，借助遗传算法对目标函数J1进行求解时，在每个优化间隔T 内，以函数的形式调用CPLEX 求解器对目标函数J2进行求解。其具体算法如下。

步骤1。通过遗传算法生成换道比例初始种群，将初始种群输入Vissim内部进行仿真运行。

步骤2。通过COM接口以遍历交通流状态结合的方法更新种群进行再次仿真。

步骤3。在每次遗传算法更新种群后进行仿真时，借助CPLEX求解器在线计算每个优化间隔内的跟车时距。

步骤4。结合路边检测器，Matlab将所优化后的数据进行反馈，实现运行参数的调整，以此优化检测到的所有车辆。

步骤5。重复上述步骤2～4，直至遗传算法关于目标函数J1求得最优值后终止。

仿真实验算法流程见图3。

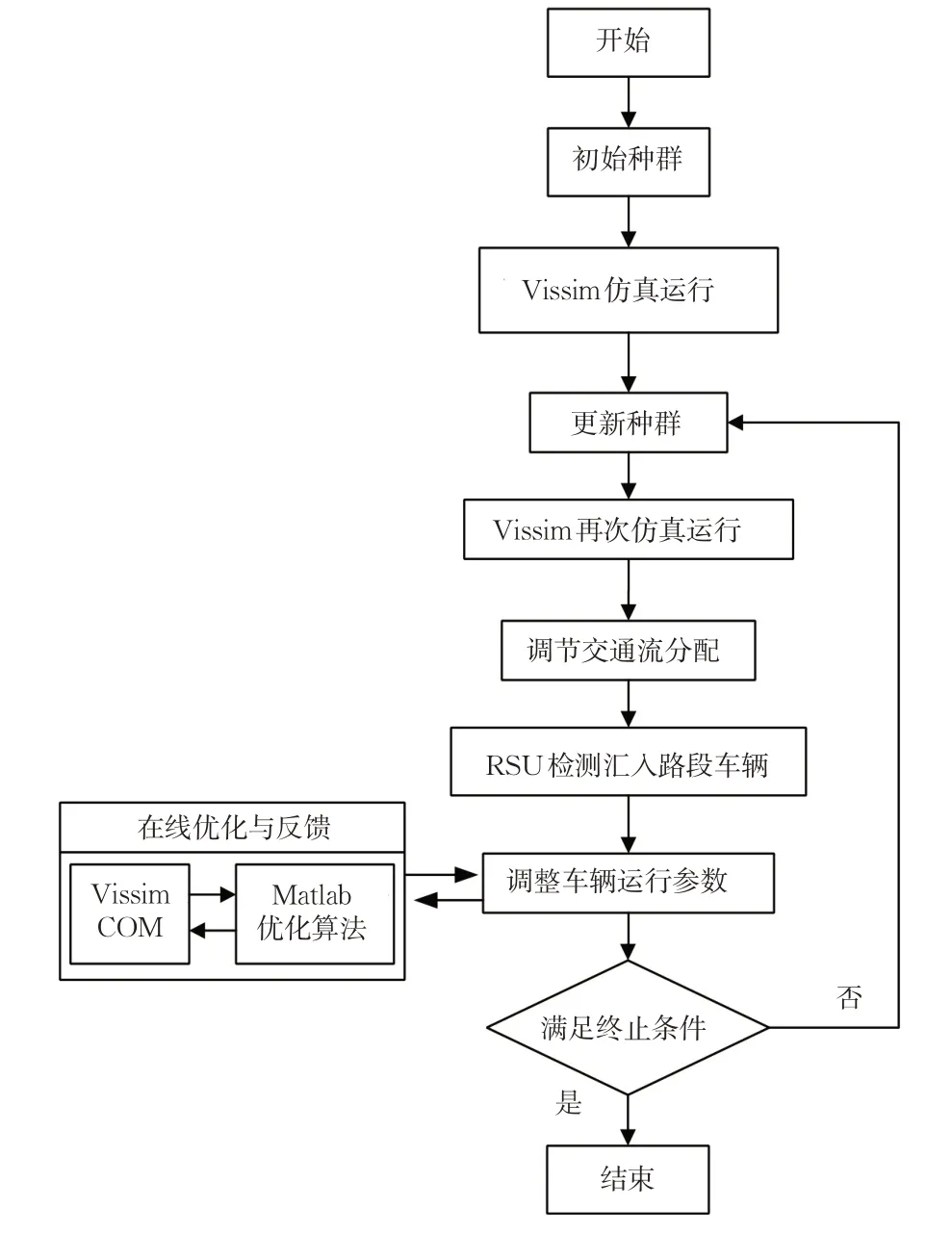
图3 仿真实验算法流程Fig.3 Algorithm procedure of simulation experiment

2.3 Vissim模型

Vissim模型为带有外车道施工区的高速公路单向双车道。为防止因交通量过大导致换道策略崩溃[18]，每条车道的初始交通量输入为500 veh/h，每隔500 s增加100 veh/h。所建立的施工区长度为200 m，汇入路段长为200 m，车辆数检测路段长度为200 m，路段m 长度为800 m，每个小路段的长度为200 m。换道控制策略各参数取值见表1。其中，l1，l2，SRF ，h*取Vissim内初始值。hidea在自由流状态能确保行车安全下进行取值[19]。 Amax与ΔA 在不影响驾驶员舒适性下进行取值[20]。ΔV1与ΔV2在不影响交通流的运行特性和交通安全下进行取值[21]。T 取值过小会导致汇入区域车辆无法及时按照要求进行跟车时距调整。

2.4 基于PET的冲突检测

Vissim 内部无法实时显示交通碰撞，但可以实时生成微观的车辆运行参数，笔者以后侵入时间（Post Encroachment Time,PET）来表示路网冲突次数，其具体表示为2辆车通过同一指定区域的时间差。在汇入部分每隔50 m进行路段冲突检测，通过RSU收集施工区交汇处PET小于1.5 s跟车状态作为交通冲突[22]。

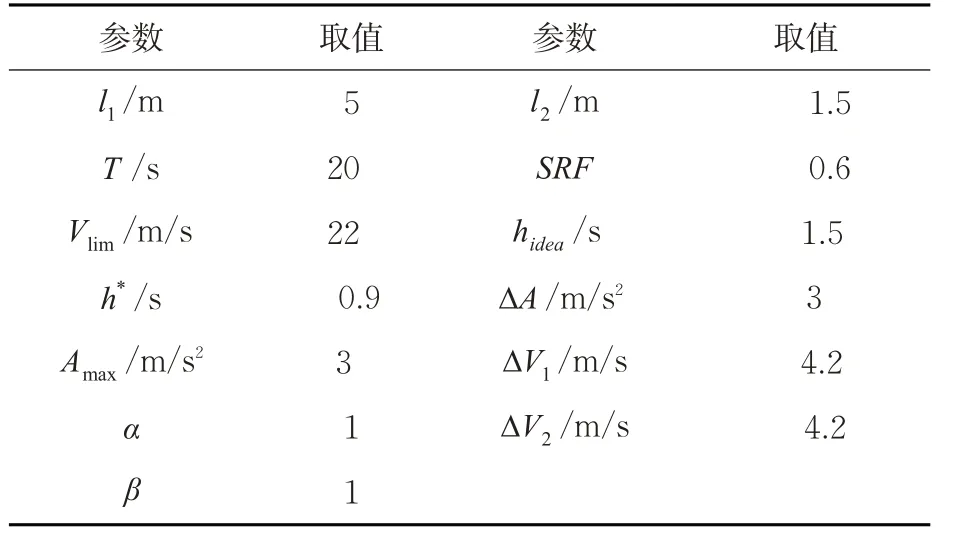
表1 换道控制策略参数Tab.1 parameters of lane change control algorithm

3 实验结果分析

3.1 可视化分析比较

在Vissim_COM/Matlab 环境中进行单步模拟仿真，设定开始的200 s 为系统预热时间，每次总仿真时长为2 200 s。在遗传算法求解换道比例过程中，每一种群代数下运行20 次Vissim。当种群代数达到20时，Vissim与Matlab停止交互，通过拟合最佳适应度（best fitness）的绝对值得到图4。此时Vissim总仿真次数为400次，总仿真时间为880 000 s。图4中，能够发现当种群代数在第5次时即总仿真次数达到100次后追踪到了最佳适应度值。

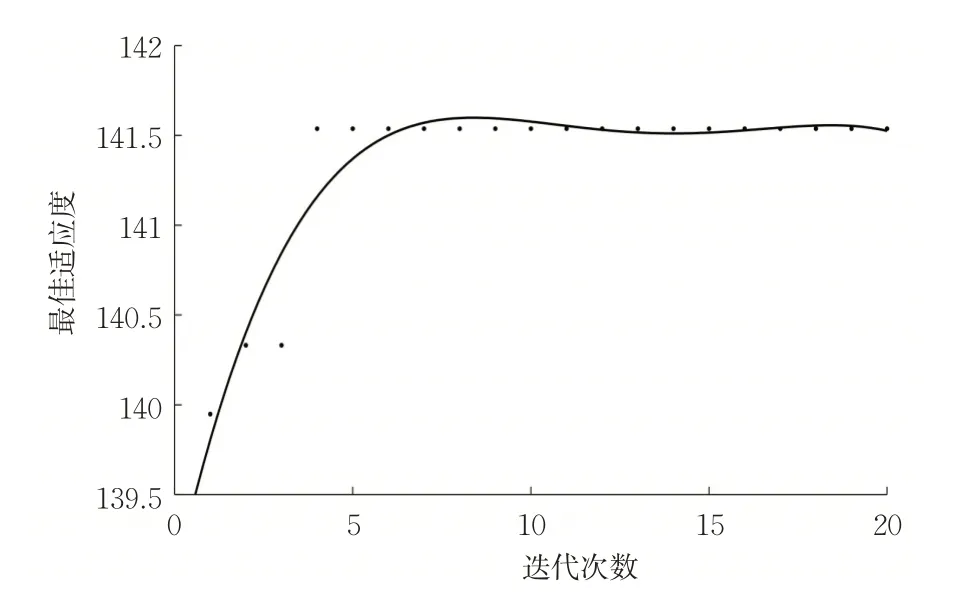
图4 最佳适应度值的变化Fig.4 Change graph of best fitness value

在结果分析中，单纯的断面检测无法较好的反应出整体车辆的运行状况，本文检测和优化的车辆均为全局车辆。其中换道优化控制策略对交通系统在运行稳定性和平顺性方面的影响以车辆运行轨迹和速度标准差指标来衡量，见图5～6。

在图5（a）～（b）中，纵坐标表示车辆位移，横坐标为仿真时间，其中每1个小点代表每隔一定时间间隔全局车辆的“曝光”位置，其中当1辆车在行驶过程中在同一位置附近被连续“曝光”时，表明该车辆行驶受阻或发生停止，表示当前发生交通拥堵现象。由每1 个小点组成具有线性关系的“斜线”代表每1辆车行驶位移轨迹。在仿真时长内，共识别到了1 079 辆车，“曝光”总数为11 829 次，即代表“斜线”有1 079条，小点有11 829个。图5（a）为未采取换道控制策略的车辆运行轨迹图，其中车辆在此处的“曝光”次数增加导致产生“黑色阴影”部分，其表示车辆在汇入路段运行受阻。能够发现当仿真步长在800 s左右时，此时交通量的输入达到700 veh/h，汇入路段开始发生拥挤，车辆运行状态变的不平稳。

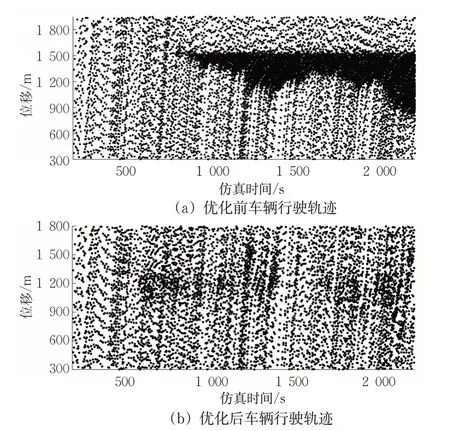
图5 车辆行驶轨迹比较Fig.5 Comparison of vehicle trajectory

图5 （b）表示采取换道控制策略后的车辆运行轨迹图，其中“黑色阴影”消失，表示车辆在汇入路段连续“曝光”次数减少，表现为此处车辆运行连续和平顺，轨迹变的“平滑”。

速度标准差对比见图6，采取优化措施前，速度标准差变化幅度较大。其中采取换道优化策略后，全局车辆的速度标准差降低了20%～40%。仿真达到800 s 后，速度标准差的变化幅度有所降低，全局车辆的速度离散性明显下降，表现为交通流稳定性有所提高，安全性得到了提升。

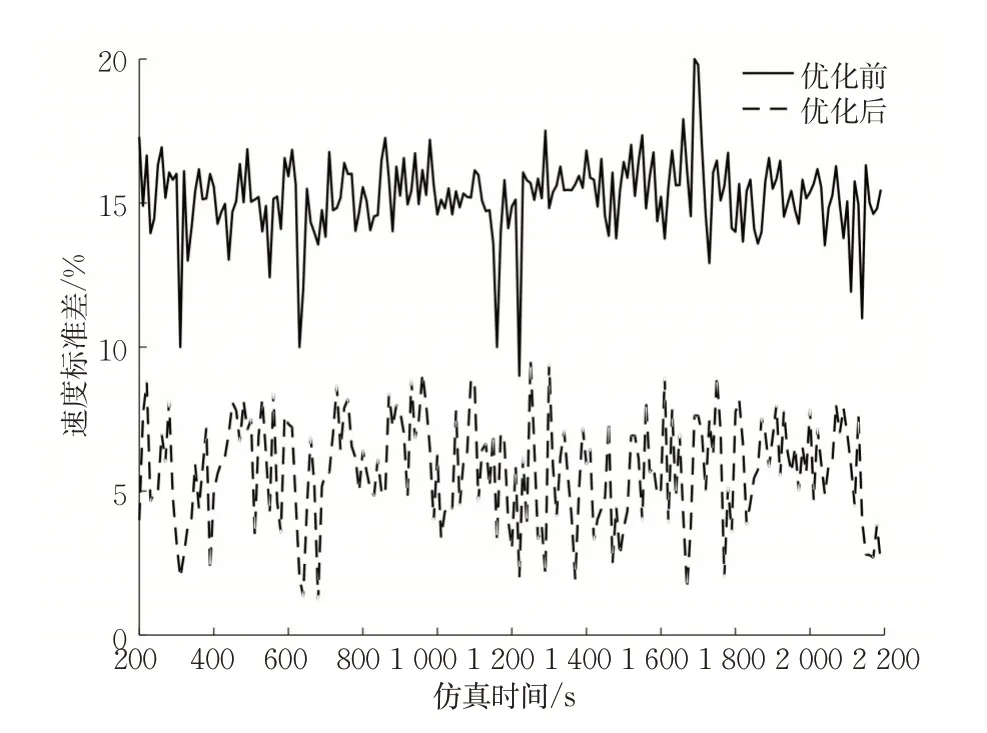
图6 速度标准差对比Fig.6 Comparison of speed standard deviation

换道控制策略对交通系统在交通效率方面的影响以全局车辆运行速度衡量。由于数据较多，变化幅度较大，并且因车辆行驶过程中的异质性而导致数据噪声较大。为了分析数据发展趋势和图形可视化后的优化控制比较，借助Matlab 中均值滑动窗函数对数据进行降噪处理，所选用窗口长度为10，降噪后的图形见图7。由于在施工区上游进行了交通流分配，会导致车辆在前期为了提前换道而使得全局车辆速度稍微降低，但当仿真步长在800 s 时，每条道路交通量的输入达到700 veh/h时，全局运行速度得到较大的提升，并且速度维持在60 km/h，此后速度变化幅度小，而此时未采取优化措施的车辆速度变化幅度大，全局速度在800 s 后逐渐降低，表现为此时车辆在汇入路段受阻导致全局运行速度降低。相比于采取措施之前全局车辆平均运行速度由42.1 km/h提高到了62.4 km/h，提高了48%。

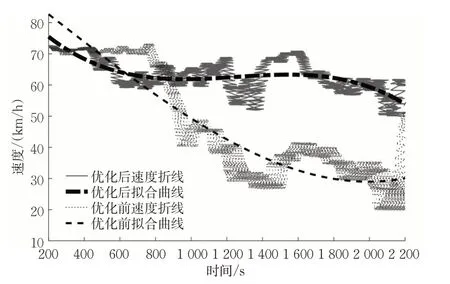
图7 全局速度对比Fig.7 Comparison of global speed

换道优化控制策略对交通系统在冲突风险评价方面的影响以全局车辆运行冲突次数衡量，见图8。图8（a）～（b）分别表示未采取和采取优化措施的冲突次数分布情况。由图中可以看到，由于冲突检测为检测施工区汇入路段，在前期由于部分车辆没有到达检测位置，所检测到的冲突次数较少。当仿真时间在800 s时，随着交通量输入的增多和汇入路段车辆堆积较多，车辆运行状态变的不顺畅，导致车辆冲突上升。800 s后，未采取优化措施的冲突分布较为集中。而优化后，主线车辆通过降低自身速度为汇入车辆制造出安全汇入间隙，使得车辆在汇入路段运行平稳，冲突分布得到改善。优化前后所检测到的PET冲突次数由32 929次降低到了19 973次，降低了39%，交通冲突得到了改善。

图8 行车冲突对比Fig.8 Comparison of driving conflict

3.2 讨论

本文实验为基于Vissim 虚拟仿真环境，其具备丰富的数据传输和应用程序接口功能，能够较好的实现所有车辆之间相互通信自动驾驶，所得数据较为理想。然而在实现换道控制策略过程中存有严格的假设，其中并没有考虑到现实因素的影响，例如自动驾驶汽车和人类驾驶员驾驶汽车的共存问题，并且模型复杂度较高，外部算法在现实中无法较好的计算并及时反馈给车辆。在仿真过程中，对于车辆加速度和跟车时距的调整减少了主线车辆激进驾驶行为，参数的调节避免了仿真软件发生外车道车辆难以汇入等失真问题。

4 结束语

1）建立了集合优化换道比例和可变跟车时距的高速公路施工区换道控制策略，以在线的方式求解线目标函数并进行实时控制，通过搭建Matlab/Vissim_COM的模拟仿真环境，分别通过分析速度标准差、运行效率和基于PET的冲突检测指标对优化前和优化后进行了评价，并且以车辆行驶轨迹作为表现形式。

2）结果表明，换道控制策略效果主要体现在仿真时间800 s后，每条车道交通量输入为700 veh/h。采取措施前，车辆从上游路段行驶到汇入路段形成车辆堆积，表现为全局车辆在汇入路段“曝光”次数增多，行驶速度下降，冲突次数增加。当采取措施后，此时汇入路段车辆连续“曝光”次数变少，全局平均速度明显提升，通过汇入路段可变跟车时距设置，汇入路段车辆堆积减少，冲突次数减少。

3）换道控制策略中提出了可变跟车时距相关理论，在未来的实际应用中，可以通过设置可变跟车时距的方法来确保车辆以较高速度安全交汇，为高速公路施工区行驶安全提出建议。

研究也存在一些不足，遗传算法和CPLEX的计算和优化时间较长，因此下一步会考虑到运用快速智能的算法应用到实车实验中。