基于不确定性的高速公路路线方案比选方法研究

肖锋 祝文君 管春光

（1.四川藏区高速公路有限责任公司，四川成都610041；2.林同棪国际工程咨询（中国）有限公司，重庆401121；

3.四川省交通投资集团有限责任公司，四川成都610041）

0 引言

高速公路施工前期重要的问题就是确定路线的最优方案，因其关系着项目的建设过程、线路质量、使用功能等产生直接影响，并影响到国家的政治、经济、国防等情况。在中国，主要的客、货运输任务由高速公路承担，对沿线所经区域的政治、经济、文化的发展都有着重要作用。高速公路路线方案比选比选结果对工程带来的影响是巨大的，且具有唯一性及不可重复性。因此，研究高速公路路线的方案比选问题具有重大意义。

在国外研究中，研究学者对于方案比选的研究前期以经济成本为主，如J.Dupuit[2]费用效益理论的观点、哈佛大学[3]提出的层级分析法、美国航空公司[4]的收益管理法。随着环境问题的不断出现及环保意识的普及，才将环境保护等因素作为重要因素来考量，如＂压力-状态-响应＂（PSR）模型[5]，OECD（经济合作与发展组织[6]在PSR模型的基础上以“可持续发展”理念将其深化解析，建立概念模型以此来评价世界环境状况。在公路路线技术发展的同时，互联网技术也在飞速发展，如Sadek等[7]开发的多目标路线决策平台；Li等[8]采用模糊算法和专家经验法来确定各评价指标的权重。

国内对于方案比选的早期发展与国外相同，即在国内建设项目经济评价的初始阶段，基本采用费用/效益分析法，如发布的《建设项目经济评价方法与参数》，张彤炬[9]等将费用效益分析方法应用于公路路线方案比选中，李海峰[10]提出以国民经济评价进行路线方案的选择，并提出具体量化方法。在中国初期的环境影响比选阶段，主要以定性分析为主，如师利明[11]等将生态理论学与公路沿线生态环境质量相结合法，后期以环境为主要因素的环境方案比选也在发生着质的变化，由定性发展为定量计算，如李林[12]通过对路线中的环境影响因素进行分析，并在此基础上论述了如何在环境环境影响下进行路线方案的选择问题。随着我国高速公路建设难度的不断加大，方案比选也随之复杂，为解决这一问题，我国学者将多目标决策法引入到方案比选中，

如田硕[13]在考虑经济、施工、环境等多因素情况下，提出了AHP-熵权法以及改进的逼近理想点方案比选法，冯婧[14]提出改进的全寿命法，并将其与AHP、灰色关联法相结合，进行各方案的全寿命周期大小排序。

目前，中国对于路线方案比选、路线安全问题研究较多，成果丰硕，而对于路线方案的安全比选的研究则较少。而路线比选中的安全问题才是需要关注的，因此，提出更全面的路线安全比选方案，并使其真正应用到项目中是刻不容缓的。为此本文在以往研究的指标体系基础上，将安全因素引入路线方案比选评价中，对评价指标体系的定性指标通过云模型理论进行相应转换，减少传递过程中的不确定性，为路线方案的安全比选评价、决策提供可靠准确的依据。

1 基于不确定性的高速公路路线方案比选评价指标体系的建立

本文从安全的角度确定了影响高速公路安全的主要因素，主要包含5个因素，通过这5个影响因素进行分析后，将其分解为包含定性、定量（效益型、成本型）的20个子目标。根据确定的5个准则层、20个子目标[15-21]，建立了基于安全因素的高速公路路线方案安全比选评价指标体系结构，如表1所示。

表1 高速公路路线方案安全比选评价指标体系Tab.1Highway RoutePlan Safety Comparison and Selection Evaluation Index System

B5最大坡长定量指标成本型指标C危险路段和路侧危险指标B7凸型竖曲线半径B6最小坡长定量指标效益型指标定量指标效益型指标B8凹型竖曲线半径定量指标效益型指标D路网布局和大型构造物分布指标B9竖曲线长度定量指标效益型指标B10运行速度协调性定性指标效益型指标B11视距 E恶劣天气影响E2对自然环境影响及引发地质灾害情况定性指标效益型指标定性指标成本型指标

2 云模型理论[22]

2.1 单规则不确定性推理

本文提出的不确定性比选方法主要应用云模型的单规则不确定性推理，其实质为定性指标的概念可通过不确定理论的云模型推理来量化，表示为If A then B，其中A、B表示两个定性概念，在发生器中代表的是推理前件与后件。

单条件单规则不确定推理的计算步骤如下：

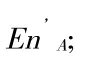
（5）最终输出N个云滴。

3 基于不确定性的高速公路路线方案比选方法

云模型的单规则不确定性推理可以在评价指标确定权重前实现定性指标到定量的转换，并保留其不确定性，但对于评级指标体系中的定性、定量指标需要先进行权重计算，因此本文提出将云模型- G1法-熵权法结合的组合赋权法。

3.1 主观权重的确定

G1发是根据专家的经验对指标的重要程度给出排序关系，并进行赋值，计算方法如下：

（1）确定序关系

按照本文确定的5个准则层、20个子目标进行重要程度排序，如专家A认为准则层中重要程度B＞A＞C＞E＞D，再对子目标中的指标进行重要程度排序后，即确定各指标间的序关系。

（2）重要程度分析

该步骤主要将20个子目标进行比较，并给出重要程度比值ωk-1/ωk（比值结果rk）。如将子目标不良地质条件与地形条件比较，若专家认为两者同样重要，则比值为1；若专家认为不良地质条件比地形条件稍微重要，则比值为1.2；若专家认为不良地质条件比地形条件明显重要，则比值为1.4；若专家认为不良地质条件比地形条件强烈重要，则比值为1.6；若专家认为不良地质条件比地形条件极端重要，则比值为1.8；若专家认为不良地质条件比地形条件稍微重要，则比值为1.2；若专家认为两个子目标相比重要程度不属于上述值，则需对重要度进行重新排序。

（3）准则层、子目标权重系数计算

完成各准则层、子目标进行重要程度赋值，通过公式（1）（2）进行各、准则层、子目标权重ωn的计算

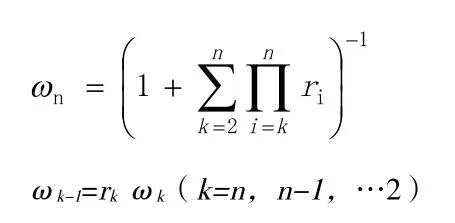
（4）群决策结果的确定

确定定性指标的主观权重时，需要邀请多名专家（t）进行赋值，因每名专家的经验各有不同，因此在赋值时会有所差异，为了避免这一结果，本文根据每名专家对方案安全比选的熟悉程度进行赋值（dk），如专家A对安全比选领域不太熟悉，则赋值结果为2；对安全比选领域一般熟悉，则赋值结果为4；对安全比选领域较为熟悉，则赋值结果为6；对安全比选领域非常熟悉，则赋值结果为8；通过公式（4）求出该专家的权重系数，再利用公式（3）[23]将对专家的赋值结果与专家对某个评价指标的赋值结果用公式（3）进行计算，则得出该评价指标的群决策结果。

3.2 熵权法确定客观权重

对于本文提出的评价指标体系，定量指标如平曲线长度是一个明确的数值，定性指标如地形条件对路线方案安全的影响首先采用语言模糊数进行取值，并转换换为云模型数。采用表2中的因子分值高低的定性评语为定性指标进行赋值，并将其转换为云模型数，结果见表2。

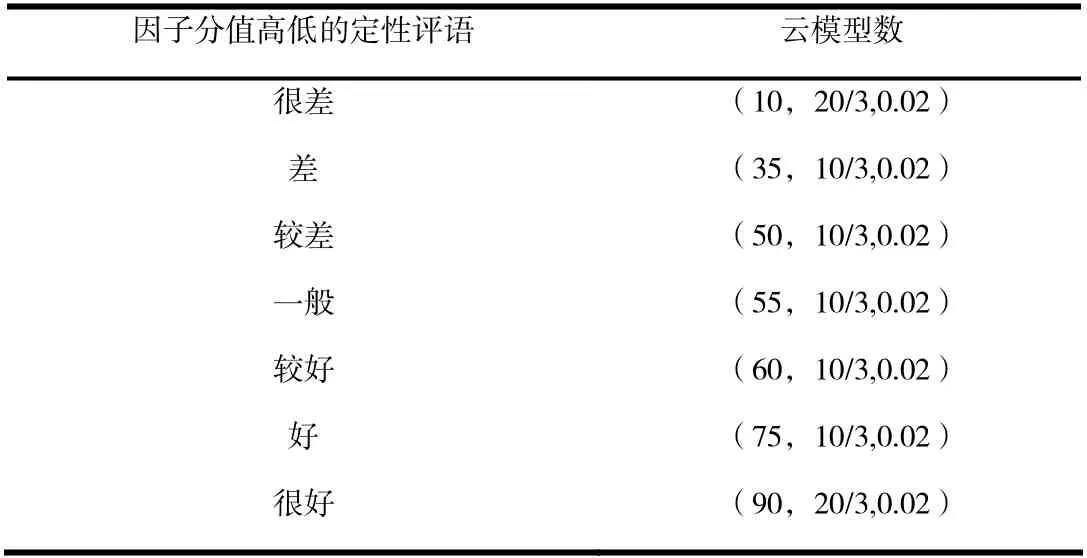
表2 语言类模糊数、云模型数的转换关系Tab.4 Relationship between fuzzy number and cloud model number of language class

本文以定性指标“地形条件”为例，利用专家的知识建立不确定性推理规则：

If地形条件“很好”，Then因子作用分值“很高”，则对应的云模型描述为（90，20/3，0.02）；If地形条件“好”，Then因子作用分值“高”，则对应的云模型描述为（75，10/3，0.02）；If地形条件“较好”，Then因子作用分值“较高”，则对应的云模型描述为（60，10/3，0.02）；If地形条件“一般”，Then因子作用分值“中等”，则对应的云模型描述为（55，10/3，0.02）；If地形条件“较差”，Then因子作用分值“较低”，则对应的云模型描述为（50，10/3，0.02）；If地形条件“差”，Then因子作用分值“低”，则对应的云模型描述为（35，10/3，0.02）；If地形条件“很差”，Then因子作用分值“很低”，则对应的云模型描述为（10，20/3，0.02）。

其次将运用云模型转换得到的定量数值得分与定量指标共同构成方案评价的决策矩阵，并应用公式（5）、（6）对效益型指标、成本型指标进行转换，最终构建新的决策矩阵S。

对构建的决策矩阵进行客观权重的计算，通过公式（7）计算某个子目标的熵值、公式（8）计算某个子目标的权重。

最后通过公式（9）将主观权重（wi）与客观权重（ui）进行组合权重的计算，组合权重需要通过公式（10）、（11）计算出结果，其中α、β分别代表主客观权重系数，α与β的乘积大于0，α与β之和等于0，且α与β值的区间为[0，1]。通过公式（10）进行主观、客观加权属性值的计算，为使公式（10）的一致水平趋于最小化，运用公式（11）的线性加权来优化模型。

将公式（11）求得的权重系数带入公式（9），获得组合权重。设λ为所有评价指标的权重组成的权重向量，则：

将组合权重的转至解与经过转换的决策矩阵S输入到方案安全比选的计算公式中，即得到方案比选的最终结果。

4 实例分析

以西南地区某高速公路为例，该条高速公路是西南地区重要的扶贫通道。项目的实施对于有效缓解周边地区的交通拥堵及冬季积雪期的拥堵情况，完善区域高速公路网布局，提升路网效率和安全性，具有重要意义。本次研究从前述建立的5个准则层进行综合分析，对路线经过不同的方案进行了比选研究，提出了K线方案（方案一）、K+B9线（方案二）、B6+C1线方案（方案三），三个同深度方案的路线走向示意图如图1所示。

图1 路线走向示意图Fig.1Schematicdiagram of theroute

三个路线方案的主要技术指标及工程规模如下表。

表3 各方案主要技术指标及工程规模

大桥m/座15597.25/26 13892/24 13798/22 中、小桥m/座190/3190/3479.9/6 桥梁合计 m/座15787.25/29 14085/2714277.9/25特长隧道m/座24203/2 24313.5/2 22589.5/3长隧道m/座7898/4 10017/511880.5/6 中隧道m/座525/11457.5/2 1146/2 短隧道m/座473/1473/10 隧道合计 m/座33099/836261/10 35616/11

通过上述计算方法，并根据每位专家的调查反馈结果计算相应的准则层、子目标的权重，并计算每位专家的权重指数，对赋权的结果进行整理，最终得到各方案对应指标取值，如表4所示。

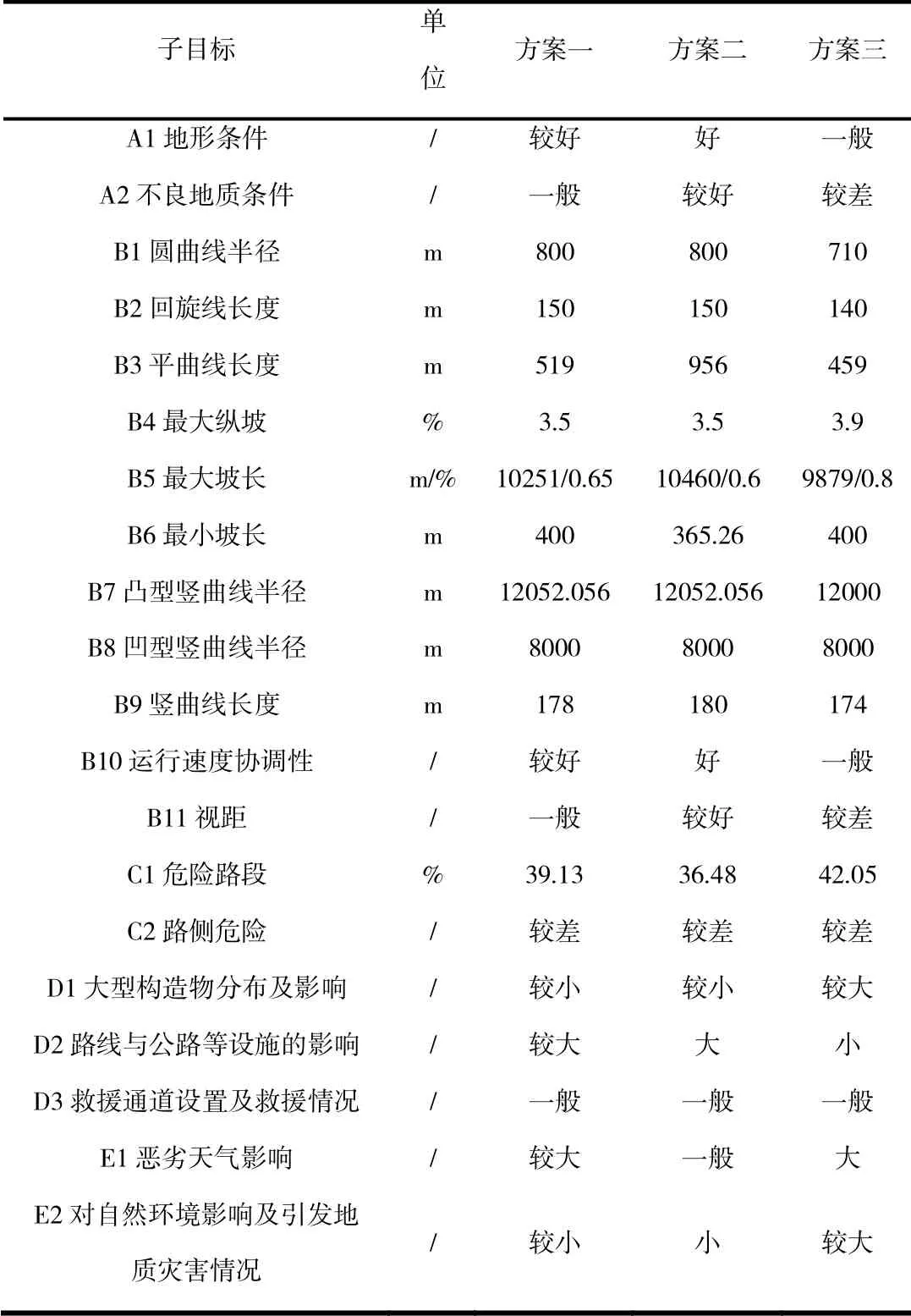
表4 各比选方案对应指标取值 Tab.4 Corresponding indicators for each comparison scheme

首先利用G1法和熵权法分别计算指标主观权重和客观权重，再根据公式（9）、（10）、（11）、（12）得到指标体系的组合权重：（0.0312，0.0775，0.0242，0.0109，0.0111，0.0364，0.0199，0.0124，0.0125，0.0147，0.005 8，0.0659，0.0312，0.2087，0.1078，0.0687，0.0741，0.0411，0.1089，0.0469）。

将组合权重的转至解与经过转换的决策矩阵S输入到公式（13）中，即得到三个方案比选的最终结果，如表5所示。

表5 方案综合得分 Tab.5 Comprehen sivescore of scheme

从表5中可以看出，按照本文方法求出的最优方案为方案二，这与实际工程比选结果保持一致。同事还可看出本文提出的方法在给出最优安全方案时，还能依据各比选方案最终求得的结果看出不同方案的差距，并可通过方案最终构建的矩阵及指标的权重赋值，找出造成不同方案分值差距的准则层及子目标，从而有效的对方案进行优化。

5 结语

（1）本文采用云模型中的单规则不确定性推理及专家为语言模糊数赋值，实现了定性指标到定量的有效转换。

（2）根据文章建立的评价指标体系，采用G1+熵权法进行组合权重的计算，并在确定客观权重前将定性指标转换为定量描述，即提出了云模型+G1+熵权的综合赋权方法，该方法即包含专家的经验，也体现了指标自身携带的信息。

（3）将本文提出的方法应用到西南某高速公路路线方案比选中，不仅实现了定性指标的有效量化，还与实际工程比选结果一致，并能根据方案最终的得分将方案进行安全性排序。