从材料力学课程到大学生创新训练的延伸教学★

祝 捷 陈霁月 曹阳阳 王建强 梁书锋 刘谨嘉

(中国矿业大学(北京)力学与建筑工程学院，北京 100083)

2018年12月，教育部高等教育司司长吴岩在建设中国“金课”的讲话中指出，课程对于大学生的影响最为直接，对于人才培养占有不可替代的重要地位，因此课程设置和课堂教学是教学中最普遍、最重要的问题[1]。事实上，课程设置的本质目标是培养学生解决实际问题的能力[2]。近年来，众多高校对于本科教育的研究性教学进行了探索和实践[3-5]。其中，中国矿业大学(北京)自2014年起开始实施本科生导师制，对于本科生创新能力的培养方式进行调整[6-11]。

对于力学类、土木类和航天类的学生而言，材料力学课程，兼具基础性和工程性的特点[12]，是一门理论性强、应用广泛的专业基础课程，包含课堂教学和实验教学两部分[13]。为了适应教育部对课程高阶性、创新性和挑战度的要求，教师在教学设计中需要重点关注学生知识、能力、素质的综合性培养，利用互动教学环境训练学生的思辨能力，采用讨论的方式，引导学生挖掘知识点的内涵，提出个性化的问题。本科生围绕提出的问题，依托大学生创新训练项目，开展探究式学习。

本文以梁的弹性弯曲问题为例，阐述从材料力学课堂教学、实验教学到综合性创新训练的延伸教学实践过程，为该类教学模式的发展提供案例支持。

1 课程教学对知识点的思考

1.1 课上对知识点的认识

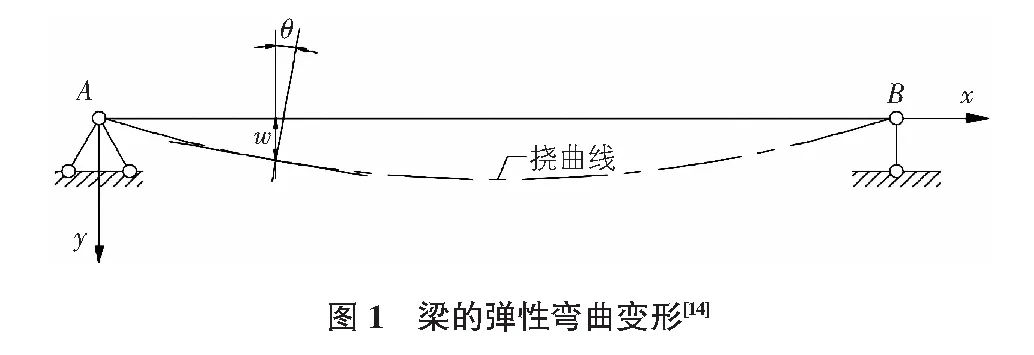
梁的弯曲变形是材料力学课程中重点讨论的问题。其中，详细阐述了梁在线弹性、小变形范围内挠曲线方程的推导过程[14]。如图1所示，由几何关系和物理关系知，曲率κ与挠度w、弯矩M间分别满足:

(1)

(2)

其中，ρ为曲率半径；EI为梁的抗弯刚度。

联立式(1)，式(2)，得到在平截面假设和假定梁纵向平面之间不因弯曲而相互挤压的条件下等直梁的挠曲线近似微分方程可表示为：

EIw″=-M(x)

(3)

将式(3)进行积分，代入边界条件，即可得到梁的挠曲线方程。

(4)

其中，C1,C2均为积分常数与边界条件有关。在已知荷载条件下，利用式(4)可得到梁的挠曲线。

1.2课后对知识点的思考

为了启发学生更加深入地思考梁的弯曲变形问题，笔者请学生对如下问题进行思考：如果梁上载荷未知，即无法计算弯矩方程通过式(4)得到梁的挠曲线方程，是否还有其他方法求解。

学生通过梳理几何方程可知，梁横截面上的正应变沿梁高度方向分布符合：

(5)

其中，ε为横截面上距离中性轴为y处的正应变。则由式(5)可知，梁横截面上任一点处纵向正应变ε与该点至中性轴的距离y成正比，其比例系数即为该截面的曲率。

学生由此可得，荷载未知条件下，通过式(5)表示的应变—曲率关系，可以求解梁的挠曲线方程，仅需将式(5)代入式(1)建立微分方程再积分即可。

2 实验教学对知识点的再认识

学生根据上述分析可知，在载荷未知条件下要得到梁的挠曲线方程，需要对应变进行测量。利用北京市高等学校实验教学示范中心的材料力学多功能实验台(见图2a))，学生对梁纯弯曲段的应变进行了测量。实验采用矩形截面等直钢梁，横截面高度h=40 mm，宽度b=20 mm，跨度L=350 mm，弹性模量E=206 GPa，泊松比ν=0.3。该实验梁的受力简图如图2b)所示。试样在两个集中荷载之间形成纯弯段，对应弯矩M等于集中荷载值P乘以加载臂长度a。

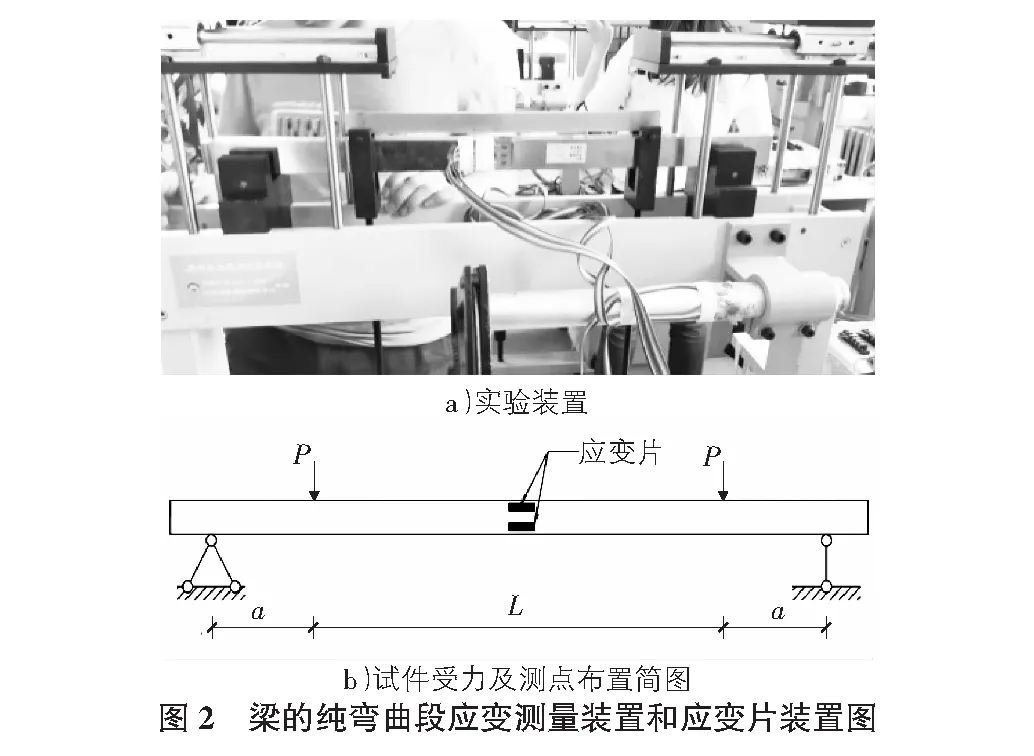
提出问题：考虑到实验中矩形截面钢梁的中性层位于梁的中部，且与梁上下表面平行，在梁同一横截面内沿梁高平行于中性轴应同时布置两个应变片。由于不知道中性轴的具体位置，故需要对3种可能存在的应变片与中性轴相对位置(如图3所示)进行讨论。

讨论结果：无论应变片与中性轴相对位置如何，均可得到截面曲率为：

(6)

其中，ε1,ε2分别为S1和S2位置上应变片测得的应变数值，其中S2位于S1下方，d为两个应变片中心的垂直距离。由于纯弯曲梁各横截面曲率相等，因此式(6)即为梁的曲率。

根据x轴向右为正，y轴向下为正，以及纵向线应变的符号规定(拉应变为正，压应变为负)，可以得到：

(7)

对纯弯曲梁，将式(7)进行两次积分得到：

(8)

实验时首先校准仪器，固定并测量加载臂长度a，然后对梁进行加载，记录4组荷载值，并读取相应的应变片测量值。实验弯矩和应变数值如表1所示。在假设纯弯段两端的挠度值相等的条件下，学生通过四组重复实验的应变数据，分别按照式(4)与式(8)计算了梁跨中与集中荷载作用点的挠度变化量wt与wc，两者对比情况见表1，其相对误差为RE。

表1 梁的最大计算挠度与理论值对比

由表1可知，基于应变测量得到的梁跨中相对集中荷载作用点的挠度变化量与式(4)得到的理论值的相对误差基本上控制在5%范围之内，说明了式(8)的有效性。

3 课程教学向创新训练延伸

通过上述梁弯曲变形问题的研究性教学实践，学生找到了基于应变测量计算梁挠度的理论依据，加深了梁变形问题的理解。学生对此类问题产生了浓厚的兴趣：如果梁因横向力作用而发生弯曲时，上述依据纯弯曲条件推导的梁挠曲线方程，即式(8)，是否会产生误差。如果误差过大，是否有减小误差的方法。学生决定将上述问题延伸到大学生创新训练项目继续探究，并邀请老师继续指导。

为了与实际工程相结合，教师组织学生赴天津市对海门大桥进行了实地调研，此外通过实验测试和数值模拟等方式进一步探究了梁式结构在荷载未知条件下的挠度计算方法。图4为本科生实地调研时测量工字型钢构件的情况。

实际工程中梁常受到均布荷载作用，此时梁的曲率值不再是常数，因此首先需要讨论梁的曲率值沿其跨度方向变化时，式(8)的有效性。考虑到实验室不具备相关的实验条件，学生用有限元法通过ABAQUS软件工字钢梁，如图5所示，进行了数值模拟。选取梁的跨度l=5 000 mm，弹性模量E=206 GPa，泊松比ν=0.3。学生模拟计算了均布荷载和纯弯曲两种条件(如图6所示)下梁的变形情况。均布荷载条件下，沿全梁纵向布置q=16 kN/m；纯弯条件下，集中力偶M=50 kN·m作用在梁的两端。图7为荷载作用下梁弯曲变形的数值模拟结果。

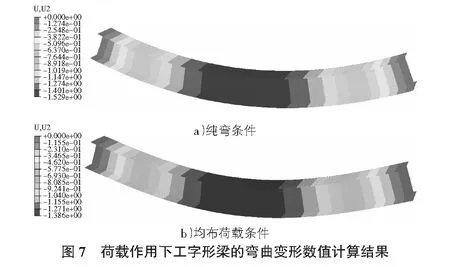
表2 拟合计算值与数值模拟结果的对比

由表2可知，纯弯条件推导得到的式(8)用于计算同样加载条件下梁的挠度，误差较小。对于受均布荷载作用的梁，由于曲率值沿梁的跨度发生变化，式(8)的计算结果误差增大。学生通过多项式拟合曲率函数的方法可以达到减小误差的目的。考虑到选取的拟合多项式具有一定的适用范围，学生们将后续研究集中到讨论拟合多项式的形式上。

4 结语

本文以梁的弯曲问题为例，阐述了教师从课堂教学出发，利用实验教学和大学生创新训练项目，引导学生对问题进行持续性的主动思考、分析解决问题的过程。教师立足于教材或实验教学内容的延伸和扩展，把一些看似普通，但是有深度或有工程应用价值的概念和原理提炼出来，引导学生进行深入地分析和理解，在教师引导下，学生首先解答老师提出的问题，然后自己提出新的问题，再依托大学生创新训练项目，进一步探究问题的答案。实践证明，密切联系重点教学内容，采用课内知识与课外思考相结合、理论推导和实验分析相结合、基本原理和工程实际、课程教学和创新训练相结合的延伸教学方法有利于激发学生的主动思考和学习兴趣，这为相关教学模式的延伸与发展提供了参考。