几何光学光路图画法分类例析
湖南 杨宗礼
光的折射定律、折射率、反射定律、全反射现象是选修3-4高考考查的热点内容,几乎每年都考,主要以计算题或选择题的形式进行综合考查。正确画出完整的光路图是解决几何光学问题的前提和关键,根据题意准确、规范地画出光路图才能找到解答问题的几何关系,解题时能找出具有代表性的光线并作出光路图,可以起到事半功倍的效果。下面笔者进行分类例析,希望对同学们有所启发和帮助。
一、常规情况
【例1】如图1所示为一透明圆柱体的横截面,其半径为R,透明圆柱体的折射率为n,AB是一条直径。今有一束平行光沿平行AB方向射向圆柱体。求:经透明圆柱体折射后,恰能经过B点的入射光线的入射点到AB的垂直距离。
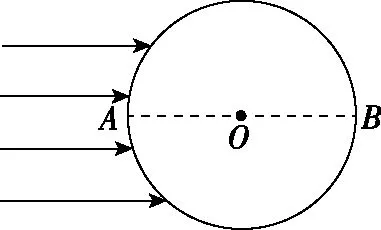
图1
【解析】设入射角为i,折射角为r,入射光线到AB的距离为h,如图2所示。
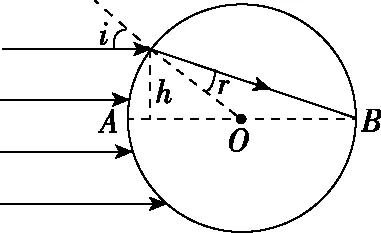
图2
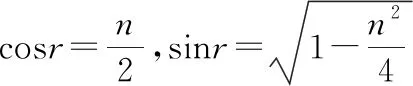
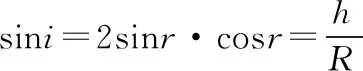
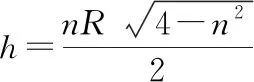
【点评】1.本题是简单的几何光学问题,其基础是作出光路图,根据几何知识确定入射角与折射角,再根据折射定律求解。
2.所谓常规情况就是研究的光线射到两种介质的界面上时,往往同时发生光的折射和反射现象。
3.解决光的折射问题的思路
(1)根据入射角、折射角及反射角之间的关系,作出比较完整的光路图。
(2)利用几何关系确定光路中的边、角关系,要注意入射角、折射角均以法线为标准。
(3)利用折射定律、折射率公式求解。
(4)注意在折射现象中光路是可逆的。
【高考真题赏析1】(2018年全国卷Ⅲ)如图3所示,某同学在一张水平放置的白纸上画了一个小标记“·”(图中O点),然后用横截面为等边三角形ABC的三棱镜压在这个标记上,小标记位于AC边上。D位于AB边上,过D点作AC边的垂线交AC于F。该同学在D点正上方向下顺着直线DF的方向观察,恰好可以看到小标记的像;过O点作AB边的垂线交直线DF于E;DE=2 cm,EF=1 cm。求三棱镜的折射率。(不考虑光线在三棱镜中的反射)
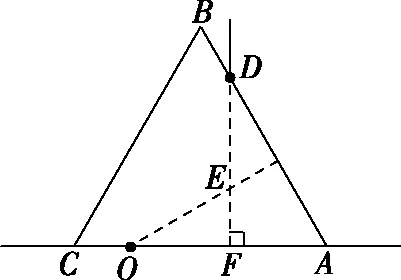
图3
【解析】过D点作AB边的法线NN′,连接OD,则∠ODN=α为O点发出的光线在D点的入射角;设该光线在D点的折射角为β,如图4所示。根据折射定律有
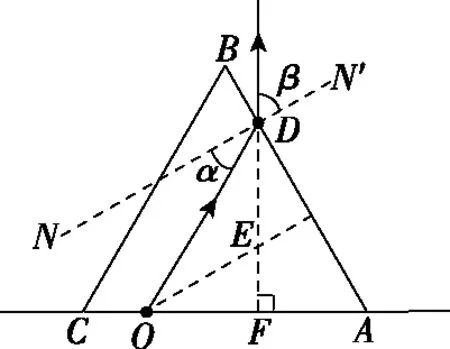
图4
nsinα=sinβ①
式中n为三棱镜的折射率
由几何关系可知β=60° ②
∠EOF=30° ③
在△OEF中有
EF=OEsin∠EOF④
由③④式和题给条件得
OE=2 cm ⑤
根据题给条件可知,△OED为等腰三角形,有
α=30° ⑥
二、临界光线

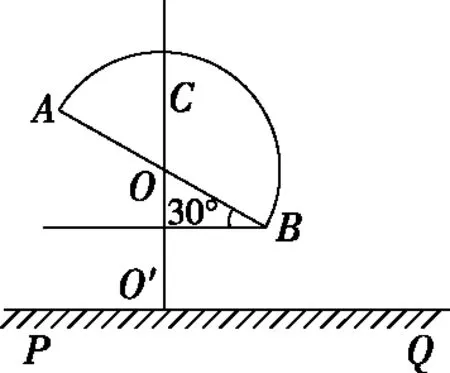
图5
【解析】如图6所示,在O点刚好发生全反射时,光在光屏PQ上的落点距O′点最远
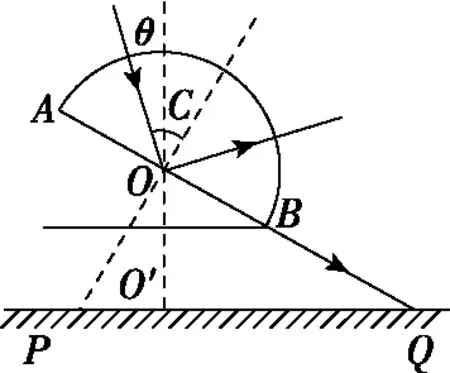
图6
解得C=45°
入射光与竖直方向的夹角为θ=C-30°=15°
【点评】1.本题属于光路中的临界问题。绕O点逆时针旋转调整入射光与竖直方向的夹角,入射角会不断增大,折射光线偏离OO′越来越远,当光线在O点刚好发生全反射,此时光在光屏PQ上的落点距O′点最远。解题关键是找出临界光线的位置,画出入射角等于临界角时的临界光路图,利用几何关系和临界角公式求解。
2.光线由一种状态变为另一种状态时,可能存在一个过度的转折光线,这种光线称之为临界光线。
3.解答光路中的临界类问题的一般方法如下:
(1)确定光是从光密介质进入光疏介质还是从光疏介质进入光密介质;
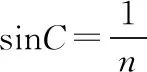
(3)根据题设条件,判定光在传播时是否发生全反射;
(4)如发生全反射,画出入射角等于临界角时的临界光路图;
(5)运用几何关系或三角函数关系以及反射定律等进行分析、判断、运算,解决问题;
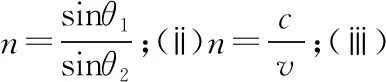
【高考真题赏析2】(2019江苏卷)如图7所示,某“L”形透明材料的折射率n=2。现沿AB方向切去一角,AB与水平方向的夹角为θ。为使水平方向的光线射到AB面时不会射入空气,求θ的最大值。
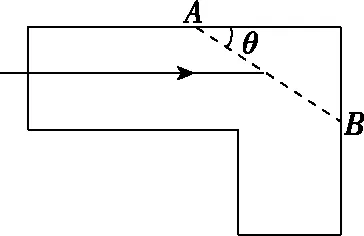
图7
【解析】要使光线不会射入空气,即发生全反射,设临界角为C,即有
由几何关系得C+θ=90°
联立解得θ=60°


图8
【解析】设光从半球壳内表面边缘上的A点入射,入射角为90°,折射角为α(全反射临界角也为α);然后在半球壳外表面内侧的B点发生折射,入射角为β,如图9所示。

图9
由全反射临界角的定义得
1=nsinα
由正弦定理得
OD为对称轴,设∠BOD=γ,由几何关系可
设B点到OD的距离为r,即为所求的半球壳外表面有光线射出区域的圆形边界的半径,由几何关系有
由上式联立及题给数据得
三、边界光线
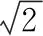
( )
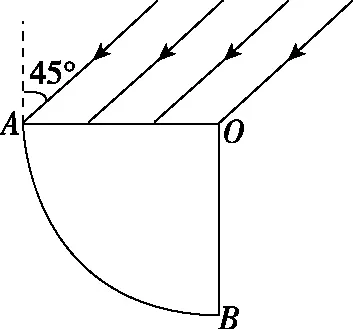
图10
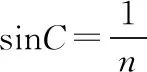
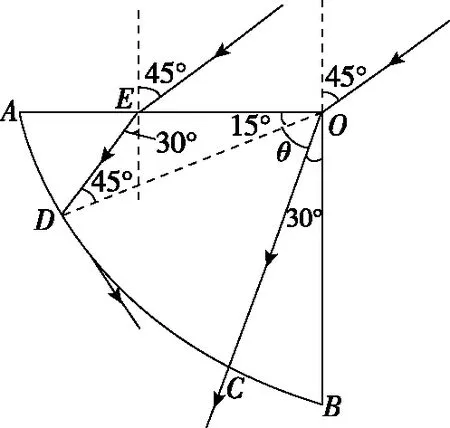
图11
【点评】1.本题求出射光束的宽度,属于光路中的边界问题。两条边界光线分别是从O点入射的光线和从E点入射的光线,画出这两条光线的光路图,然后运用折射定律与全反射规律结合三角形知识求解。
2.所谓边界光线是指光在传播过程中,通过光学仪器或遮光屏的边缘或端点的光线;亦指一束出射光中两条最边缘的光线。
3.解答光路中边界类问题的一般思路
(1)根据题设条件找准两条边界光线
求出射光束的宽度,关键是找边界光线,如果发生了全反射,恰好发生全反射的临界光线就是一条边界光线,另一边界光线要通过分析找出;
(2)画出两条边界光线的光路图。
(3)运用折射定律、全反射规律以及三角形知识等进行运算解决问题;
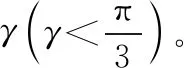
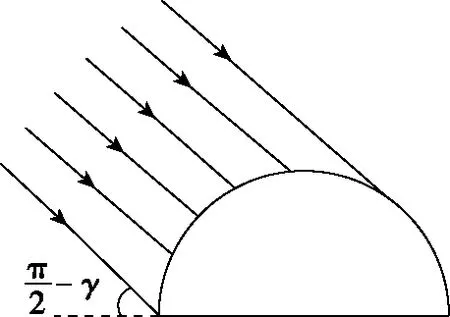
图12
【解析】在半圆柱形玻璃砖横截面内,考虑沿半径方向射到圆心O的光线1(如图13),它在圆心处的入射角为θ1,满足θ1=γ①
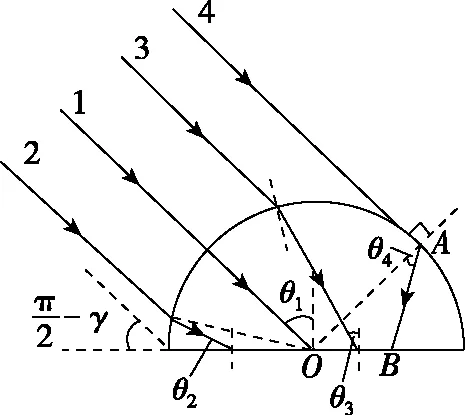
图13
θ1恰好等于全反射临界角,光线1恰好发生全反射。
在光线1左侧的光线(例如光线2)经过柱面折射后,射在玻璃砖底面上的入射角θ2满足θ2>γ②
因而在底面上发生全反射,不能直接折射出。
在光线1右侧的光线(例如光线3)经柱面折射后,射在玻璃砖底面上的入射角θ3满足θ3<γ③
因而在底面上不能发生全反射,能从玻璃砖底面射出。
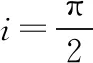
由折射定律知,经圆柱面折射后的折射角
∠OAB=θ4,满足sini=nsinθ4⑤
式子中,n是玻璃的折射率,由全反射角的定义知
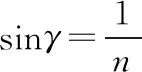
联立④⑤⑥式得θ4=γ⑦
由几何关系可得∠AOB=γ,故底面上透光部分的宽度
四、对称性在光路中的应用
【例4】如图14所示,一玻璃工件的上半部是半径为R的半球体,O点为球心;下半部是半径为R、高为2R的圆柱体,圆柱体底面镀有反射膜。有一平行于中心轴OC的光线从半球面射入,该光线与OC之间的距离为0.6R。已知最后从半球面射出的光线恰好与入射光线平行(不考虑多次反射)。求该玻璃的折射率。
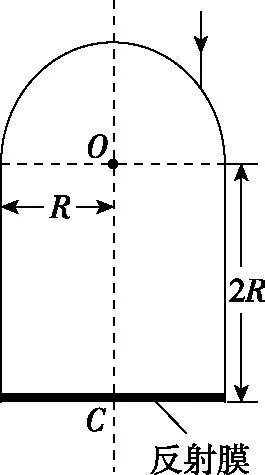
图14
【解析】如图15所示,根据光路的对称性和光路可逆性,与入射光线关于OC轴对称的出射光线一定与入射光线平行。这样,从半球面射入的折射光线,将从圆柱体底面中心C点反射。设光线在半球面的入射角为i,折射角为r。由折射定律有sini=nsinr①
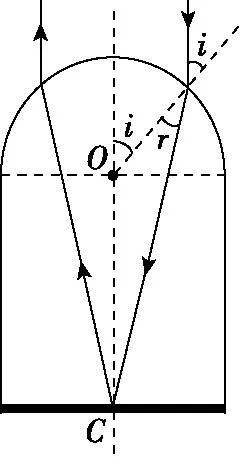
图15
由正弦定理有

由几何关系,入射点的法线与OC的夹角为i
由题设条件和几何关系有
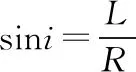
式中L是入射光线与OC的距离
由②③式和题给数据得
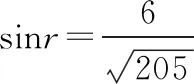
由①③④式和题给数据得
【点评】1.本题的关键条件是出射光线与入射光线平行,依据出射光线与入射光线对称,可判断光线将从圆柱体底面中心C点反射。画出光路图,运用平面几何便可运算。
2.对称性解读:入射到光学元件的光线再从光学元件出射时,出射角与入射角相等,则出射光线与入射光线对称;反射光线与入射光线关于法线对称,平面镜成的像与物关于镜面对称。
3.此类问题解题关键
利用对称性分析常常可使问题变得简单易解,能快速解题的关键在于根据对称性准确找出光线在元件内部的入射点或出射点并正确作出光路图。
【高考真题赏析5】(2017年全国卷Ⅱ)一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图16所示,容器右侧内壁涂有反光材料,其他内壁涂有吸光材料。在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率。
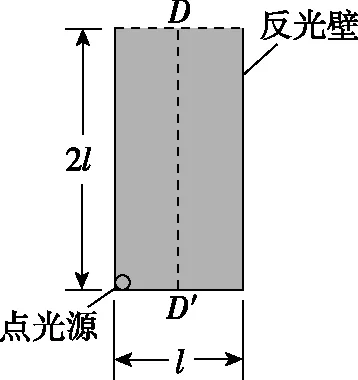
图16
【解析】设从光源发出直接射到D点的光线的入射角为i1,折射角为r1。在剖面内作光源相对于反光壁的镜像对称点C,连接C、D,交反光壁于E点,由光源射向E点的光线,反射后沿ED射向D点。光线在D点的入射角为i2,折射角为r2,如图17所示。设液体的折射率为n,由折射定律有
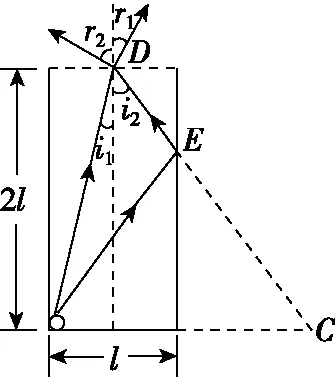
图17
nsini1=sinr1①
nsini2=sinr2②
由题意知
r1+r2=90° ③
联立①②③式得
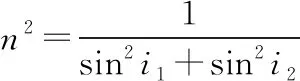
由几何关系可知
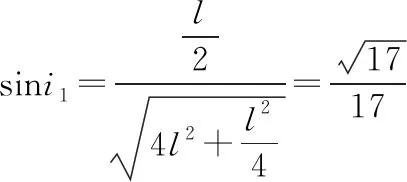
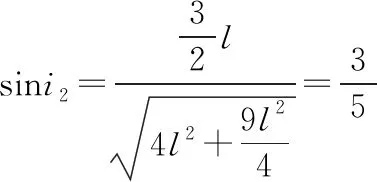
联立④⑤⑥式得
n≈1.55
【点评】本题作出光路图的突破口是准确找到光线射到反光壁的入射点,由于物像对称,反射光线的反向延长线一定过像点,DC连线与反光壁的交点E为入射点。


