Helmert方差分量估计在GPS/GLONASS/BDS/Galileo组合定位权比确定中的应用

代 阳，刘 超

(安徽理工大学 测绘学院，安徽 淮南232001)

随着全球导航卫星系统(global navigation satellite system,GNSS)的不断完善与发展，多模GNSS系统组合与兼容成为了目前卫星组合导航定位的主要方法[1-2]。在众多导航系统中，因为美国的全球定位系统(global positioning system,GPS)，俄罗斯的格洛纳斯系统(global navigation satellite system,GLONASS)，中国的北斗系统(BeiDou navigation satellite system,BDS)与欧盟的伽利略系统(Galileo satellite navigation system,Galileo)精度高，可靠性强，成为了目前卫星导航定位的主流系统。相较于单系统，采用GPS/GLONASS/BDS/Galileo多系统组合导航定位能够覆盖更加广泛的时空域，提供更加充足的可视卫星，优化星座结构，稀释几何精度因子，从而提高定位的可靠性和稳定性[3-4]。同时在算法方面，组合导航定位通过不同系统的组合，削弱了单系统中的系统性误差。而且，多系统提供的适量冗余数据能够改善由于过少观测量而导致的法方程病态问题，并为选星提供更多更优的选择策略，从而进一步提高定位的精准度。因此采用GPS/GLONASS/BDS/Galileo组合导航定位，能够提供更优更可靠的导航定位服务。

在多系统组合导航定位中，伪距单点定位模型由于无需固定整周模糊度，解算速度快，被广泛运用于生产实践中。该模型采用最小二乘算法，解算精度受几何模型与随机模型精度影响。且各个系统的观测值权阵组成了随机模型，反映了各个观测值对定位解算的贡献大小，因此观测值权阵是影响定位精度的重要因素。在多系统伪距单点定位时，如果仅采用等权及高度角模型定权，简单地将总观测值糅合起来，笼统地将各类系统观测值分为一类，而忽略不同系统之间星座结构与导航性能差异所带来的各类观测值之间精度不同的不利因素，反而会降低定位精度[5-6]。因此，如何确定各个系统间的权比，对提高GPS/GLONASS/BDS/Galileo组合伪距单点定位的精确度至关重要。

常用于确定导航定位权阵的随机模型通常分为：等权模型、信噪比模型、M残差法、最优不变二次无偏估计法与赫尔默特方差分量估计法(Helmert variance component estimation，简称Helmert)等。其中，因Helmert方差分量估计能够通过每个历元预平差得到残差改正数，实时估计各个系统间伪距观测值的验后单位权方差，进而得到系统间权阵，被广泛应用于多系统组合的导航定位中[7-9]。在GPS/GLONASS组合定位中，段举举等[10]和高晓等[11]采用Helmert方差分量估计对GPS、GLONASS两个系统进行定权分析，得出伪距单点定位时的合理权比为2∶1，载波定位时的合理权比为1∶1，且在该权比下，定位的精度与可靠性明显提高。在GPS/BDS组合定位中，由于北斗星座的特殊性，刘天骏等[12]将北斗卫星分为地球静止轨道、中地球轨道、倾斜地球同步轨道三类轨道卫星，针对在部分观测情况下中地球轨道卫星数量过少的问题，将指数加权与Helmert方差分量估计结合，有效地提高了静态与动态单点定位的精度。在GPS/GLONASS/BDS组合定位中，刘金海等[13]采用Helmert方差分量估计在单点定位中将各个系统间的权比设置为5∶1∶1，相对定位中的权比为1∶1∶1，其定位结果与等权模型相比具有明显的改善。在现代GNSS组合导航定位发展中，GPS与GLONASS系统正在不断完善，BDS系统逐步投放卫星完成全球组网，Galileo系统也在发挥着越来越大的作用，GPS/GLONASS/BDS/Galileo四系统组合定位俨然成为导航定位的主流。鉴于各个系统的差异，合理设置系统间的权重对提高定位精度具有重要的意义。

1 四系统组合单点定位的函数模型

GPS/GLONASS/BDS/Galileo伪距单点定位的观测方程为[14]：

(1)

采用Klobuchar模型消除电离层延迟，Saastamoinen模型进行对流层延迟改进[15]。将观测方程进行线性化：

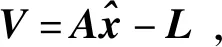
(2)

方程中的各个变量的表达式如下：

(3)

(4)

(5)

(6)

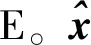
2 四系统组合单点定位的随机模型

2.1 高度角定权模型

卫星的定位精度会随着自身位置发生改变，通常认为这些精度与卫星的高度角呈正相关。在卫星信号的传播过程中，其观测值的质量会受到电离层、对流层以及多路径效应的影响，而这些误差的影响随着卫星高度角的增加而不断减弱，达到天顶方向时，受到的影响最小。目前，高度角定权模型的常用函数有两类，分别为三角函数高度角模型和指数高度角模型，其表达式分别为[16]：

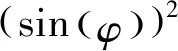
(7)

(8)

其中：P为该卫星观测值的权值；φ为卫星高度角；s为与实测数据相关的比例因子；φ0为参考高度角；a0与a1为经验系数。由于本研究使用的是分布在全球的9个站点的数据，若运用指数高度角模型，相应参数需根据不同站点的情况做出调整，且较难获取。故选择三角函数高度角模型。

2.2 Helmert方差分量估计

GPS/GLONASS/BDS/Galileo四系统的Helmert方差分量估计的步骤[17]：

1) 根据各个系统的伪距观测值，系统之间的初始经验权比设置为PG=PR=PB=PE=1，同一系统内部通过高度角方式定权。高度角的定权公式为：

(9)

式中，P为权值；i代表G、R、B或E；k代表某颗卫星的序列号；φk为第k颗卫星的高度角。

2) 对观测方程进行预平差，计算出各类系统观测值改正数V；

3) 通过严密Helmert方差分量估计，计算出各个系统的单位权方差因子θ:

θ=S-1W；

(10)

式中各个变量计算如下：

(11)

(12)

(13)

N=NG+NR+NB+NE，

(14)

N=AΤPA，

(15)

式中，nG、nR、nB与nE分别代表GPS、GLONASS、BDS与Galileo系统的观测值个数。

4) 利用各个系统单位权方差θ，对系统间的权阵重新赋值：

(16)

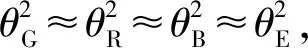
3 实验及分析

3.1 实验数据

本研究实验数据由MGEX实验网[18]提供，数据分别采集于北半球亚美尼亚的ARUC站点、日本的GMSD站点与菲律宾的PTAG站点；位于赤道中心附近的马来西亚的ANMG站点、印度尼西亚的CIBG站点与巴布亚新几内亚的PNGM站点；位于南半球新西兰的AUCK站点、位于澳大利亚的KAT1站点和STR1站点。以上9个站点均可以接收到GPS/GLONASS/BDS/Galileo系统的观测数据。实验数据从2018年9月15日0时开始采集，到2018年9月19日24点结束；采样间隔为30 s，各站点采集14 400历元(由于PTAG站点在2018年9月19日的观测文件不包含BDS与Galileo系统，故PTAG站点该天数据舍弃)。每个站点的真实坐标由IGS组织(ftp://garner.ucsd.edu/pub/docs/station_logs)提供。

3.2 实验案例

为了验证Helmert方差分量估计应用于GPS/GLONASS/BDS/Galileo四系统组合伪距单点定位中的正确性，在上述采集数据中分别使用等权模型与Helmert定权模型进行对比实验。在进行伪距单点定位解算时，统一设置其截止高度角为15°，采用L1波段的伪距观测值，电离层误差采用Klobuchar模型进行修正，对流层误差采用Saastamotion模型进行改正。以IGS站提供的站点参考坐标作为真实值，算出两种定权模型在各个站点的东方向E、北方向N、天顶方向U的方向偏差与点位偏差，并统计出它们的均方根误差(root mean square,RMS)进行比较。

由于不同历元各个系统的可视卫星数目不同，而每颗卫星的位置与状态也会随着时间不断变化，因此每个历元的GPS/GLONASS/BDS/Galileo四系统伪距观测值的权比并非固定不变。在每个历元解算前，采用Helmert方差分量估算出各个系统间的权比，用于改善伪距单点定位的随机模型，并求取每个站点各个系统单位权方差的平均值，进而得到权比。其结果如表1所示：

由表1可知，通过统计各个站点的共14 400历元的GPS/GLONASS/BDS/Galileo系统间权比得知，由于不同地区地理位置存在差异等多方面因素影响，不同站点的四个系统间的权比稍有不同，但总体的趋势大致相同。GPS、Galileo系统的权比整体大于GLONASS系统，且由于此时北斗系统尚未完成全球组网，上述站点接收到的北斗卫星数量不多，定轨精度不高，所以计算出的BDS系统的权比是最小的。

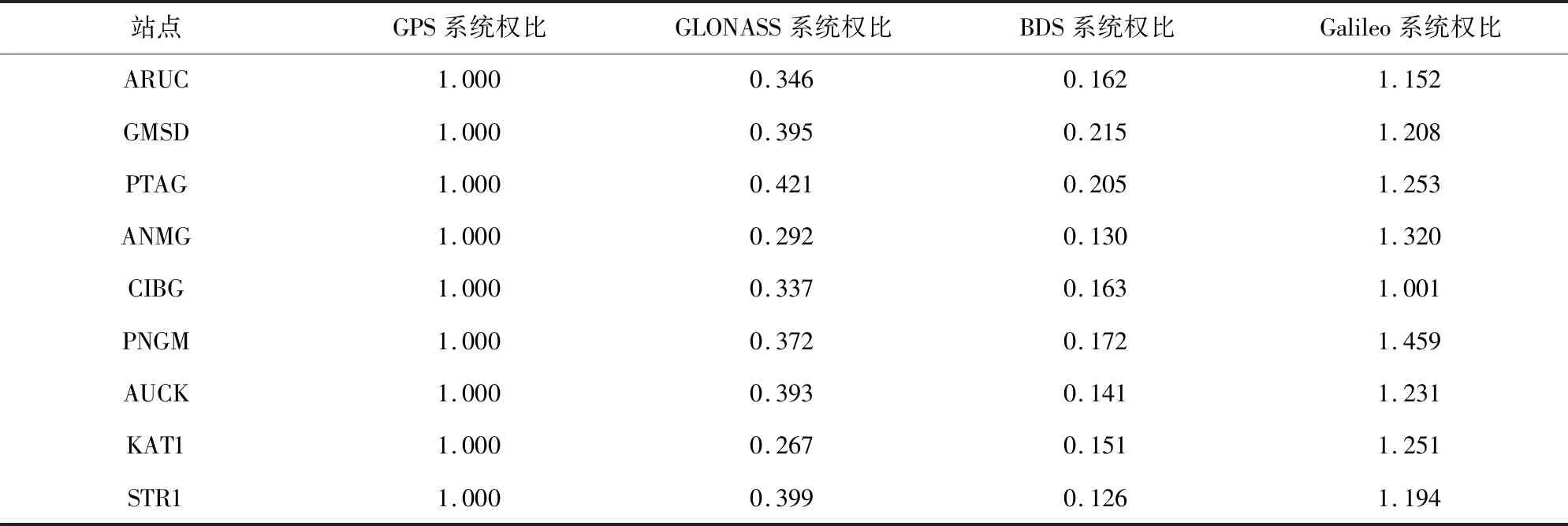
表1 各个站点的GPS、GLONASS、BDS和Galileo系统间权比Tab.1 Weight ratio between GPS,GLONASS,BDS and Galileo systems at each station

将各个站点每个历元由Helmert方差分量估计得到的系统间权比代入对应的历元中，对伪距单点定位中随机模型进行改正，计算出由该模型改进后的每个历元在E、N以及U方向的方位偏差与点位偏差。并将上述结果与等权模型的定位结果对比，其结果如表2所示。限于篇幅，上述9个站点不能全部呈现，以位于北半球的GMSD站、赤道附近的PNGM站与南半球的KAT1站共3个站点为例，分别绘制出在Helmert定权模型与等权模型下的E、N、U的方向偏差，如图1～3所示。

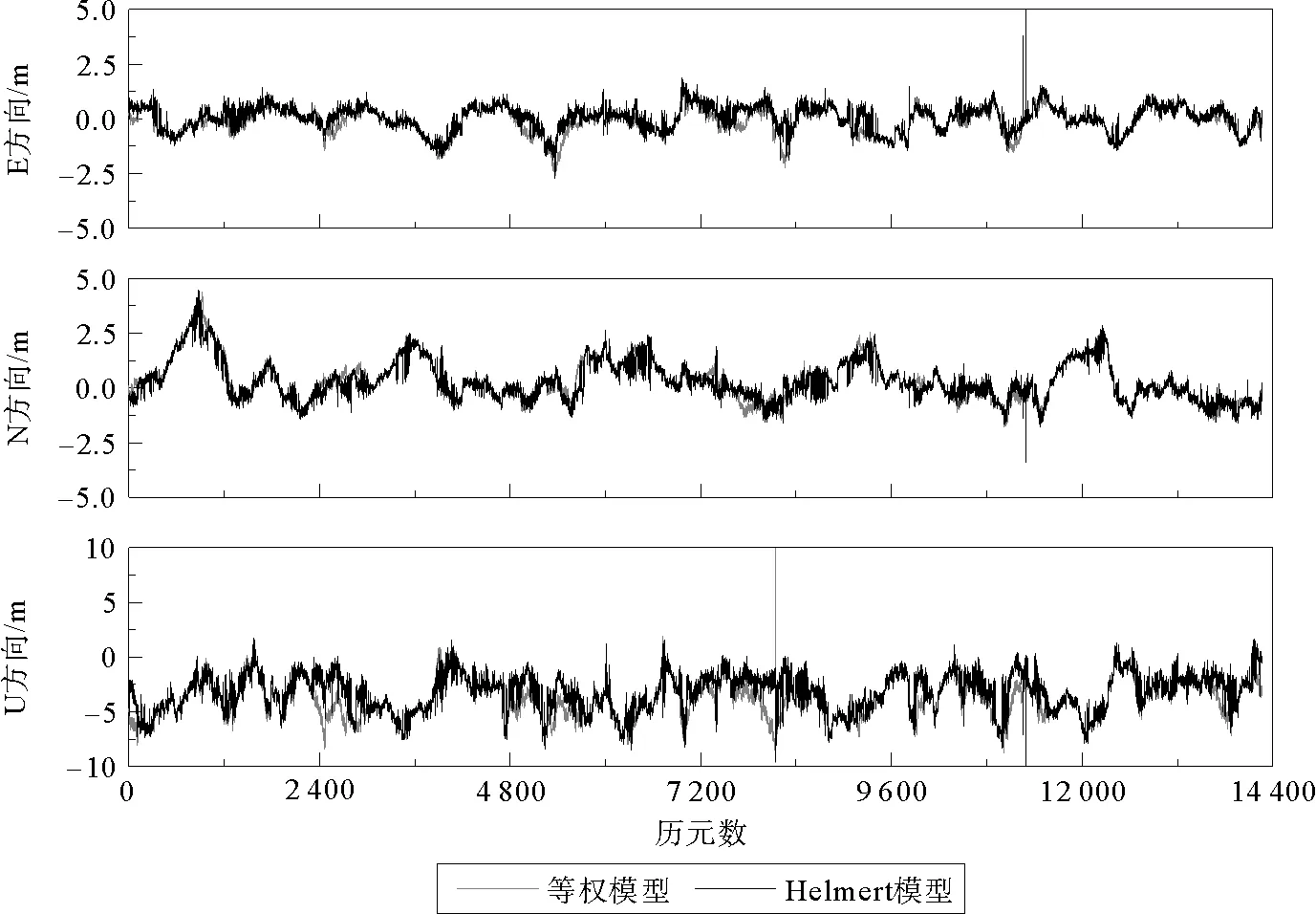
图1 两种定权方式下GMSD站的定位误差Fig.1 Positioning error under two weighting methods in GMSD station

由图1～3可知，采用Helmert方差分量估计进行系统间定权，这三个站点在E、N和U方向上的定位结果均优于等权模型。在E方向上，各个站点的定位精度提升幅度较小；而在N方向上，PNGM与KAT1站点精度提升较大；在U方向上，GMSD站点与PNGM站点较KAT1站点的精度提升更加明显。

由表2所知，上述的9个站点采用Helmert定权的伪距单点定位结果在N、E、U的方向偏差与点位误差的RMS基本上小于由等权模型的解算结果。对比相同站点的N、E、U方向偏差的RMS，发现Helmert方差分量估计在不同方位的定位精度改善程度各有差异。在E和N方向改善程度最高的是ANMG站，精度分别提升了29.0%与22.9%；在U方向改善程度最高的为PNGM站，精度提升了16.0%。对比不同站点的点位误差，发现Helmert方差分量估计在不同站点的定位精度的改善程度也不同。其中PNGM站的点位误差改善程度最高，提升了15.6%；CIBG站的改善程度最低，仅为3.69%。其他各站的点位误差改善程度基本都在10%左右。

表2 两种定权方式下各站点的计算结果统计Tab.2 Statistics of calculation results of each site under two different weighting modes

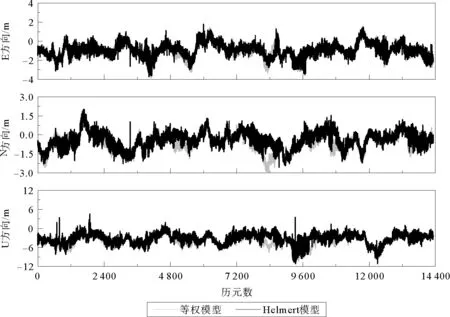
图2 两种定权方式下PNGM站的定位误差Fig.2 Positioning error under two weighting methods in PNGM station

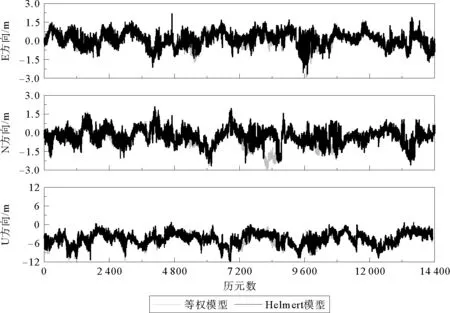
图3 两种定权方式下KAT1站的定位误差Fig.3 Positioning error under two weighting methods in KAT1 station

综上可知，在伪距单点定位中，通过Helmert方差分量估计进行系统间定权得到的定位结果精度均优于等权模型的解算结果。证明了GPS/GLONASS/BDS/Galileo四系统间的伪距观测值的精度存在差异，通过Helmert方差分量估计确定系统间的权比，改善权阵进而优化随机模型，能够有效提高定位精度。

4 结论

对GNSS组合导航定位中如何通过确定系统间的合理权比，提高定位精度的问题进行了讨论，得到以下结论：

1) 与等权方案相比，采用Helmert方差分量估计定权方案的解算结果精度在N、E和U方向上整体得到了提升；

2) 采用Helmert方差分量估计定权在不同地区中定位结果的改善效果不同，其中PNGM站改善程度最为明显，提升了15.6%；CIBG站的改善程度最低，仅为3.69%；

3) 采用Helmert方差分量估计在相同站点中的不同方向上改善程度存在差异。对于N或E方向，采用Helmert方差分量估计的定位精度高于等权模型；而对于U方向，采用Helmert方差分量估计的优势更为明显，其在全部站点均取得了良好的效果；

4) 在对多系统组合定位时，建议采用Helmert方差分量估计确定系统间的相对权比，以提高定位的精度与可靠性。

本研究仅对伪距单点定位下GPS/GLONASS/BDS/Galileo四系统间的权比进行讨论，并未考虑到北斗系统内部处于不同轨道卫星的定位精度差异，这是下一步的研究方向。