基于贝叶斯信息更新的无人机目标搜索策略研究

李 悦，周长银

(山东科技大学 数学与系统科学学院,山东 青岛 266590)

军事和灾害救助中，目标搜索是目前无人机应用中的一个重要方面。相对于人工搜索，无人机搜索目标受困于对目标信息的掌握程度和无人机搜索策略，需要更好的决策算法。

针对目标搜索问题的研究，Koopman[1]早在第二次世界大战期间就提出了基本的目标搜索理论，基于目标静止、均匀分布以及在搜索区域内匀速连续搜寻的假设，提出了发现概率模型。在Koopman的假设下，Frost[2]通过设计“扫地”实验对发现概率和扫海宽度等作了详尽阐释；Koester等[3]提出基于搜寻区域大小、扫海宽度和搜索努力程度的发现概率计算方法。为了突破均匀分布假设的限制，Brown[4]考虑了在离散空间中对移动目标进行搜索的最佳策略问题。周涛[5]对海上搜寻中发现概率的预测值进行研究,但没有提出针对扫海宽度等因素的更好策略。在海上搜索中，影响发现概率的核心因素是扫海宽度。吴翔等[6]就这一因素进行重点探讨，并提出了扫海宽度的修正模型和指数探测函数的修正模型。王博研[7]将影响发现概率的因素结合起来考虑，提出了计算初始搜寻区域中搜寻成功率的方法。上述文献提出的模型和方法，在研究无人机目标搜索问题时值得借鉴和参考，但所给搜索过程都是确定性的，不能利用搜索过程获取的新信息实时地更改搜索策略。

2011年，Stone等[8]利用贝叶斯方法提出搜寻失事飞机的数学模型，找到了坠落近两年的法航447。2015年，Lu等[9]利用贝叶斯推理给出了最优搜救模型。Lu[10]着重研究了坠毁飞机的定位方法，确定救援区域和搜索策略。

在关于无人机目标搜索的研究中，多无人机协同搜索问题得到研究人员的更多关注[11-12]。协同搜索假设目标所在区域服从均匀分布。该假设在目标位于搜索区域的分布信息未知的情况下是合理的，但若目标所处位置有明显的分布特征，则需要其他假设。

本研究借助贝叶斯信息更新方法，研究利用无人机进行目标搜索策略问题，提出目标搜索的动态策略和相应算法，并在正态分布假设下进行数值模拟，验证所给方法的适用性。

1 基于贝叶斯更新的发现概率模型

发现概率是指目标100%位于某一个区域时，无人机发现该目标的概率。发现概率的大小与无人机搜索区域面积有关，也与无人机搜索设备扫视面积有关。假设无人机采取平行搜索，执行搜索任务时的扫视宽度为ω，搜索设备单位时间的扫视距离不变，并假设每个搜索阶段的搜索面积相同。

为便于计算发现概率和确定最优搜索区域，采用离散化方法，把目标所在区域Ω分割为N个边长为ω的正方形区域R1,R2,…，RN。假设目标位置的初始信息集合记为D0，根据D0可以给出目标位于Rk的先验概率为P(BRk|D0)[13]，k=1,2,…,N,其中BRk表示目标位于区域Rk这一事件。

记R(t)是第t阶段的任务搜索区域，假设R(t)是由R1,R2,…，RN中m×n个相连的小正方形R1(t),R2(t),…，Rm×n(t)组成，此时，无人机实际搜索区域面积为mnω2，且

R(t)={R1(t),R2(t),…，Rm×n(t)}⊂{R1,R2,…,RN}。

AR(t)表示无人机在区域R(t)内搜索时发现目标这一事件，则目标被发现的概率为

(1)

其中P(ARi(t)|BRi(t),Dt-1)表示目标位于Ri(t)时发现目标的概率[14]，表示为

(2)

其中zi(t)表示在R(t)内每一小区域Ri(t)上的扫视距离。则由(1)式，有

(3)

当搜索进行到t阶段时，可以通过多种方法确定最优搜索区域[15-16]。本研究以发现概率确定最优搜索区域，发现概率根据式(1)算出。原则上，选取发现概率P(AR(t)|Dt-1)最大的区域R(t)作为搜索区域。

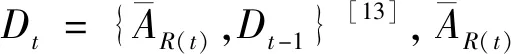
(4)

t+1阶段的目标搜索区域R(t+1)由m×n个相连的小正方形R1(t+1),R2(t+1),…,Rm×n(t+1)组成，可表示为：

R(t+1)={R1(t+1),R2(t+1),…,Rm×n(t+1)}⊂{R1,R2,…,RN}，

则t+1阶段目标位于区域Ri(t+1)(i=1,2,…,m×n)上的先验概率P(BRi(t+1)|Dt)可由(4)式给出，进而由(3)式，可计算t+1阶段目标被发现的概率P(AR(t+1)|Dt)。

以上搜索区域的确定过程可以重复进行下去，直到目标被发现为止。若经过s个阶段才发现搜索目标，则“前s个阶段搜寻发现目标”的累计发现概率定义为：

(5)

2 最优搜索策略

单位时间搜索设备内扫视距离v0称为扫视速度。假设无人机在一次搜索任务中的最大停留时间为T。最优搜索策略是在给定条件下发现概率最大的策略，记为Z(t)={Z1(t),Z2(t),…,Zmn(t)}。

最优搜索策略可由如下规划给出：

(6)

这里要求v0T≥mnω，即无人机的扫视面积v0Tω不小于实际搜索面积mnω2，在实际应用中是合理的。

结合以上分析，给出基于贝叶斯更新的最优搜索算法如下：

Step 1:给出初始先验分布P(BRk|D0)；初始值v0,T,n,m；t=1；

Step 2:根据(6)式求解t阶段的最优搜索策略(Z*(t),R*(t))；

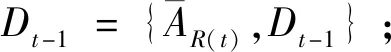
Step 4:利用(4)式，更新先验分布P(BRi(t+1)|Dt)，计算发现概率P(AR(t+1)|Dt)；

Step 5:令t=t+1，返回Step 2。

需要注意，如果在下一阶段搜索前，有额外信息获得，例如获得目标位置的新线索，这时需要对信息集Dt-1的更新进行干预，加入额外信息。同时，搜索区域目标位置的先验分布也可能发生变化，相应地，须对先验分布P(BRi(t)|Dt-1)重新调整，具体调整方法在下节数值实验中给出。

3 数值模拟

在目标搜索的研究中，通常把目标最有可能的位置坐标称为基点，基点可能不止一个。设M是基点个数，fk(x,y)是目标位于第k个基点所在区域内的概率分布，假设fk(x,y)为二维正态分布。

3.1 无贝叶斯干预下的模拟实验

目标位于区域Rk内的初始概率计算公式：

(7)

假设在Ω内有5个基点A、B、C、D、E，以这5个基点将Ω划分为5个区域，每个区域又划分为3×3个等面积的小区域。5个区域的概率分布以及概率信息如表1所示。

表1 概率分布与概率Tab.1 Probability distribution and probability

根据(7)式计算每个区域在该区域概率分布下的概率，然后挑选出概率最大的三个区域作为任务区域。接着将任务区域的概率进行归一化，公式如下：

(8)

其中n为选择出的任务区域ΩR的个数。

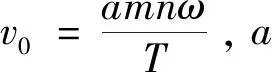
为了避免实验的偶然性，取a∈[1,2]，间隔为0.2进行实验。对最优搜索策略模型进行求解可得每个阶段的发现概率如表2(表中用P1代替P(BR1|D0)，P2代替P(BR2|D0)，P3代替P(BR3|D0))。

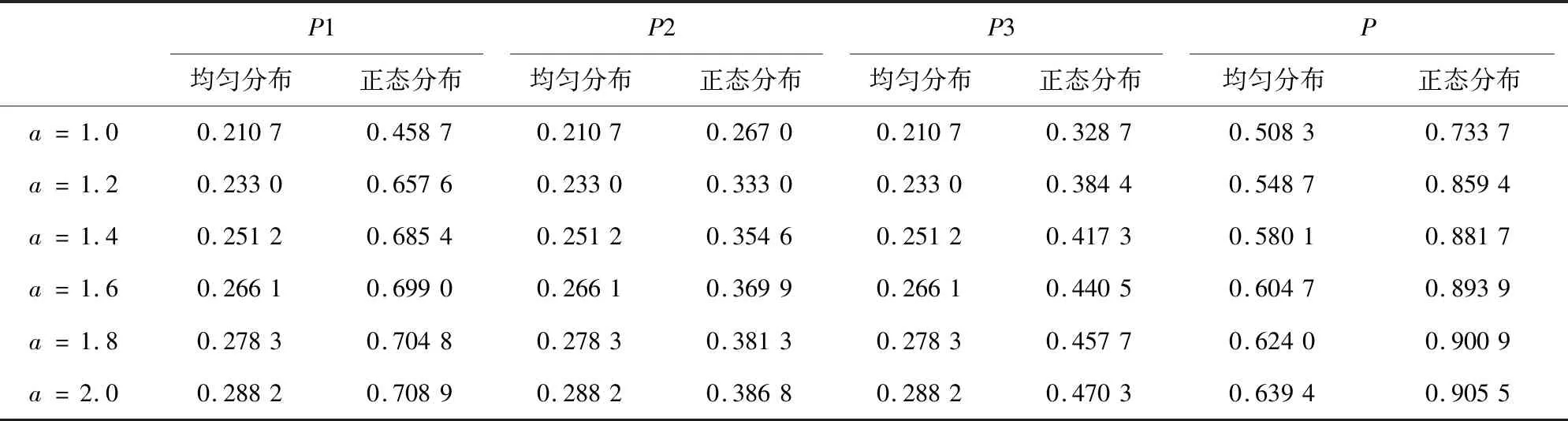
表2 无贝叶斯干预的发现概率Tab.2 Probability of discovery without Bayesian intervention

从表2中可以看到，选取正态分布比均匀分布得到的累积发现概率更大。这是由于均匀分布在目标所处搜索区域的概率分布是相同的，但是正态分布在目标所处搜索区域的概率分布在正态分布的峰值处最大，因此累计概率更大。在正态分布与均匀分布下，每阶段发现概率的变化分别如图1和图2所示。

从图1和图2中可以看出，不论是正态分布还是均匀分布，每个阶段的发现概率都随着a的增大而逐渐增大。说明扫视面积系数a对发现概率有一定影响，但是根据图1和图2中直线之间的距离来看，发现概率的增大与a的增大不是线性关系。

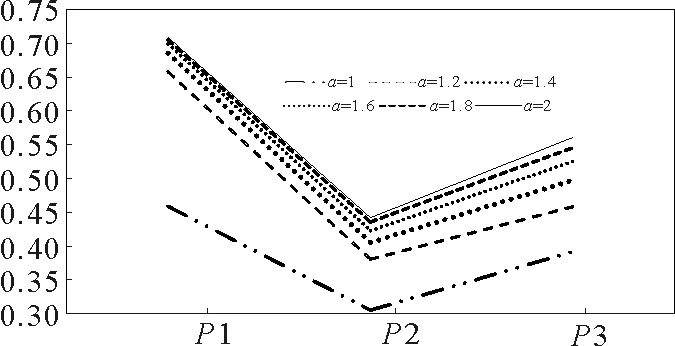
图1 正态分布下每阶段发现概率Fig.1 Probability of discovery at each stage under normal distribution

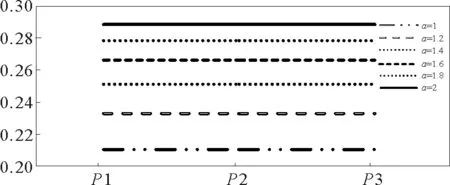
图2 均匀分布下每阶段发现概率Fig.2 Probability of discovery at each stage under uniform distribution

3.2 有贝叶斯干预下的模拟实验

在3.1节实验中加入贝叶斯干预，即在完成第一阶段搜索之后，加入一个新的信息NF(-6,13;8,8;0)，pF=0.52>pA，则更新F区域为第二阶段搜索区域，A区域为第三阶段搜索区域，此时每个阶段的发现概率如表3。

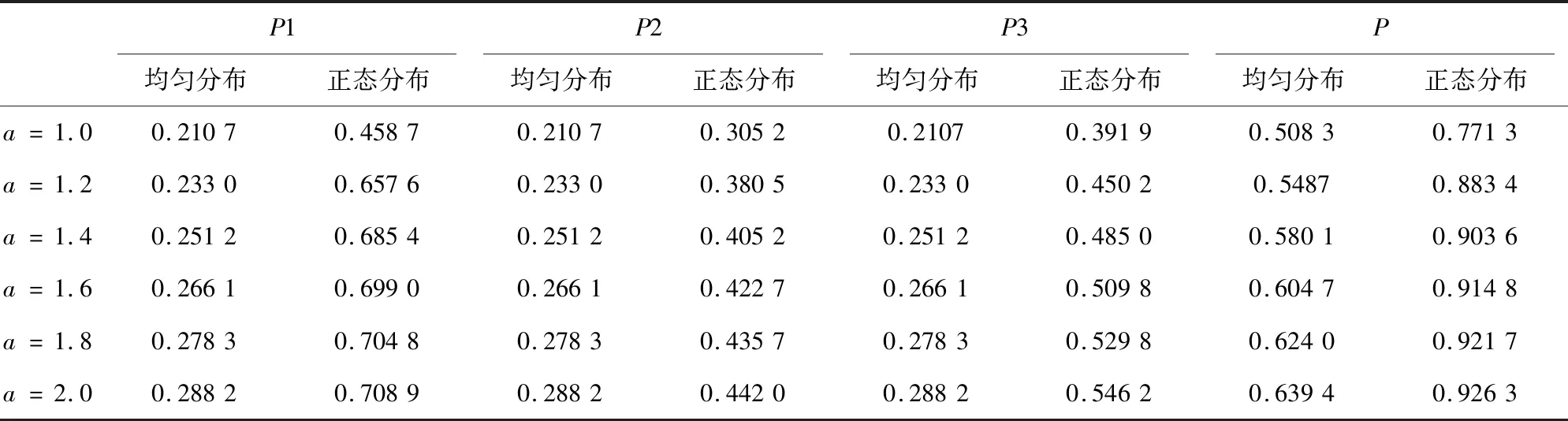
表3 贝叶斯干预下发现概率Tab.3 Probability of discovery under Bayesian intervention

从表2和表3中可以看出，加入贝叶斯干预后，第一阶段的发现概率是相同的，说明贝叶斯干预对干预前一阶段的发现概率没有影响；而第二阶段与第三阶段的发现概率均有增加，这是由于加入贝叶斯干预后，概率分布重新调整，干预后新加入的区域比原区域目标存在的概率大，因此发现概率也增大，累计发现概率也会增大。图3给出了有贝叶斯干预和无贝叶斯干预情况下的累计发现概率对比。

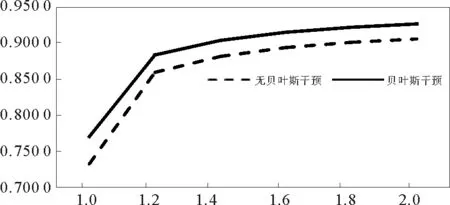
图3 有无贝叶斯干预下累计概率对比Fig.3 Comparisons of cumulative probability with and without Bayesian intervention

从图3中能够明显看出在加入贝叶斯干预后累计发现概率增大，尤其是a=1到a=1.2时，增长趋势明显。这是由于加入贝叶斯干预后，概率进行重新分配，第二阶段与第三阶段所占概率比相较之前较高，因此发现概率增大，累计发现概率也会增大。

4 结论

在已有文献中，大都假设目标位于搜索区域位置的分布为均匀分布，但通常情况下，由于预先获取了目标所在区域的分布以及该区域的地理特点信息，容易推断目标在某一些基点上的分布概率可能大一些，在其他位置则可能小一些。因此，在已掌握这些信息的情况下，均匀分布的假设就显得不尽合理。本研究首先确定目标的初始先验分布，然后计算每个目标在相同区域内的初始概率，选择合理的任务区域后，将任务区域概率归一化，最终得到目标在搜索区域上的概率分布，最后给出最优搜索策略。基于贝叶斯更新思想，利用贝叶斯公式获取目标信息的后验分布，进而由所给目标搜索策略模型做出决策，保证了搜索信息在不同阶段的动态传递性。同时，由于使用贝叶斯干预，在贝叶斯更新过程中能够采用目标新信息，使得所做决策更具实时性和合理性。

所给模型也有一定局限性。首先，在对海上搜索目标制定搜索策略时，由于目标随洋流漂流移动，会带来较大误差。解决这个问题，可以通过对正态分布密度函数进行改进，加大基点在洋流方向上概率分布的拖尾来实现。其次，没有考虑多无人机协作的搜索策略问题，搜索成本、无人机最大工作时间等因素也是需要进一步考虑的问题。