改进正则化对动态光散射含噪数据的反演研究
马光耀,曹茂永,,马凤英,纪 鹏
(1.山东科技大学 电气与自动化工程学院,山东 青岛 266590;2.齐鲁工业大学 电气工程与自动化学院,山东 济南 250353)
颗粒粒径及其分布情况是衡量颗粒产品优良性最为重要的参数,粒径的大小及分布情况直接决定了由颗粒生产所得产品的性能以及环境污染程度的判别[1-2]。动态光散射技术(dynamic light scattering,DLS)具有非接触、测量速度快等诸多特性,在颗粒粒度分布(particle size distribution,PSD)检测方面得到了广泛应用[3-4]。然而,此方法在检测过程中存在比较大的缺陷:当测量数据含有微小扰动或噪声时,会导致最终检测结果与真实结果有较大差距。所以在运用该方法时需要尽可能地去除噪声的影响,将病态不适定方程问题转换成一个与之近似的适定方程问题求解[5-7]。
目前,已有很多关于动态光散射反问题的优秀研究方法被提出,最为常用且拥有较好反演精度和抗噪能力的是Tikhonov正则化[8]和截断奇异值(truncated singular value decomposition,TSVD)正则化[9]方法。其中,Tikhonov正则化法是通过引入正则化参数和稳定泛函来设定滤子函数,从而改善矩阵的病态性;截断奇异值正则化法是通过设定滤子函数把容易造成观测数据噪声放大的小奇异值进行截断处理[10-13],从而将不适定的病态问题转换成适定问题并得到结果。为了让Tikhonov和TSVD算法反演得到更好的效果,文献[10]将Morozov偏差确定正则参数的迭代原理运用到DLS含噪数据反演中,在一定程度上优化了低噪声单峰颗粒粒度的反演精度,但是该迭代算法的终止参数却难以确定;林东方等[11]、郭家桥等[12]通过对奇异值矩阵的小奇异值部分进行修正减小了一定的正则化误差引入量,虽然该方法引入的是小奇异修正值,但引入量中仍存在部分未能及时修正的奇异值,导致结果出现偏差;王雅静等[14]提出以小波正则化与对反演问题进行分解,用Tikhonov正则化、TSVD正则化分别对粗尺度、细尺度进行寻优并处理,得到了具有较好抗噪性以及准确性的结果,但该算法计算量大且寻优过程中需保证非负性,难度较大。在模拟实验过程中,发现Tikhonov相对于TSVD而言,反演结果的平滑性更好;而TSVD的抗噪性、精确性更好一些[15]。
本研究在Tikhonov正则化法和TSVD正则化法的基础上,通过对两者滤子函数的研究[16-17],提出一种将TSVD和Tikohonv相结合的新正则化方法TTSVD,并对动态光散射含噪数据进行模拟反演实验。通过将反演结果与真实值、Tikhonov算法结果、TSVD算法结果进行比对,发现新算法有较好的精度和抗噪性。
1 动态光散射及Tikhonov、TSVD反演原理
1.1 动态光散射原理
在动态光散射测量技术中,粒度分布函数是根据归一化光强自相关函数[18]获得的:
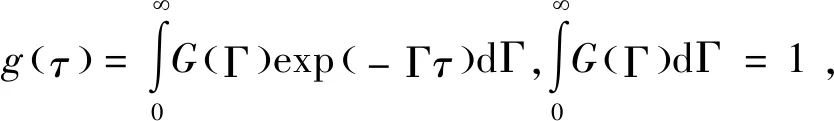
(1)
其中,τ是延迟时间,Γ为Rayleigh线宽,又称衰减率。若想求PSD结果,需要在求得衰减线宽分布函数G(Γ)之后,根据平移扩散系数公式和Stokes-Einstein关系进行求解。为求解衰减线宽函数G(Γ),将式(1)进行离散化得:
(2)
式中:j表示相关器的采样通道序列,i是样品颗粒粒径分级数。式(2)可以用矩阵形式进行简写:
Ax=b,
(3)
其中:xi=G(Γi),bj=g(τj);矩阵A的元素ai,j=exp(-Γiτj)。对方程(3)进行求解即可得到PSD结果。
1.2 Tikhonov正则化和TSVD反演理论
DLS反演问题即是对病态不适定方程(3)的求解问题,理论上可由最小二乘的求解问题来替换:
(4)
假设矩阵A∈Rm×n(m≥n),根据奇异值分解理论,对矩阵A进行奇异值分解得:
(5)
式中,U=(u1,u2,…,um)∈Rm×m,V=(v1,v2,…,vn)∈Rn×n,Σ=diag(σ1,σ2,…,σn)∈Rn×n,σ1≥σ2≥…≥σn为奇异值,ui、vi分别是矩阵A的左、右奇异向量。
所以,理论上的最小二乘解为:
(6)
由于奇异值矩阵中含有非常小的奇异值,当测量数据b包含微小噪声或受到轻微扰动时,xLS就会产生非常大的随机波动,求取的结果会非常不稳定[15]。
Tikhonov正则化是通过引入展平泛函将不适定问题近似转换程适定问题,并进行近似求解:
(7)
式中,L是正则算子,x0为解的初始估计,λ为正则化参数。当x0=0,L取单位矩阵时,Tikhonov正则化可表示成:
(8)
在选取适当的正则参数后,即可求得正则解:xTikhonov=min{Mλ[x,b]}。
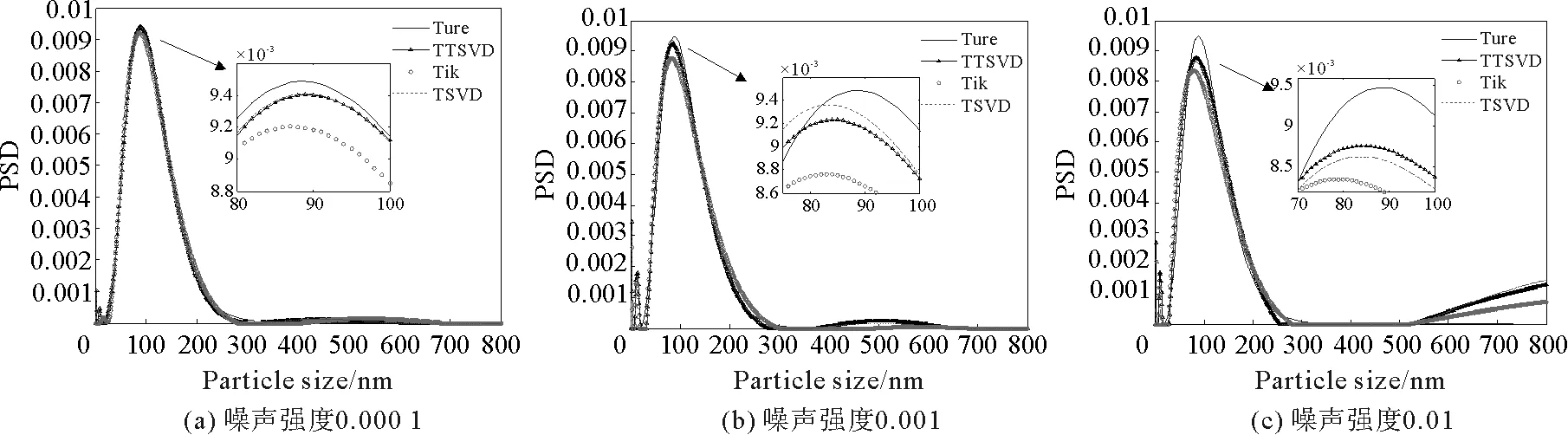
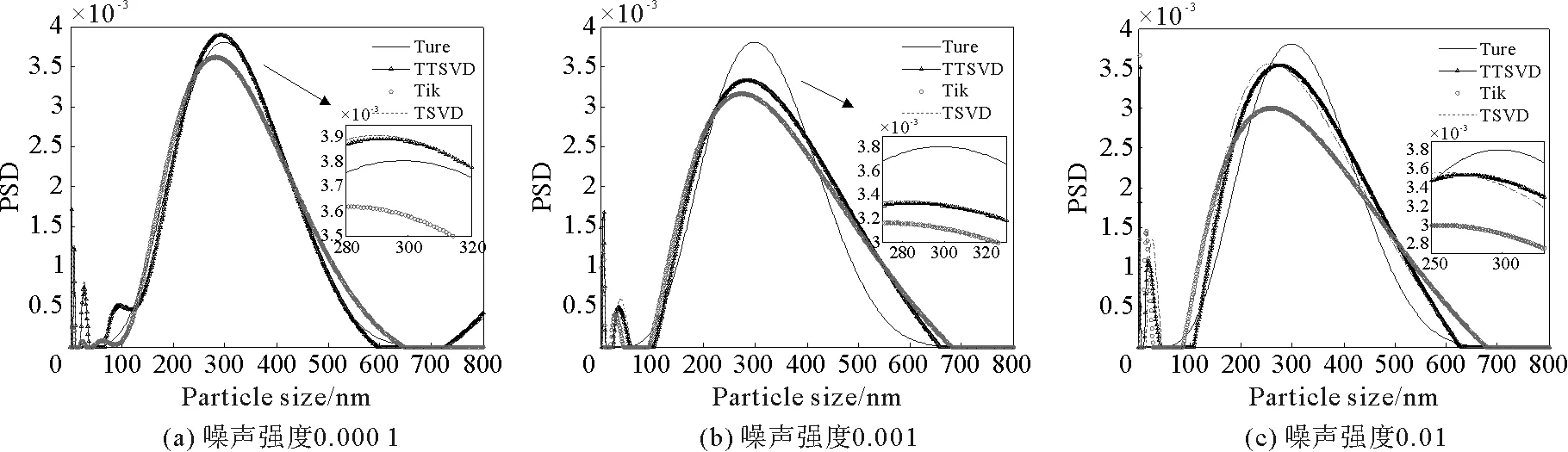
TSVD正则化是通过将奇异值矩阵中使得数据中噪声进行放大的小奇异值部分进行截断,从而消除观测数据中噪声对结果的影响。为了避免小奇异值对正则解的影响,当任意k (9) 根据Lanczos奇异值分解理论可知,在方程病态时,奇异值σn是一个非常小的近似为0的值,且奇异值σ1远大于σn。矩阵A中较大的奇异值及其相应的左右奇异向量构成了其数值模型中的可靠部分,而小奇异值及其相应的左右奇异向量构成了数值模型中的不可靠部分。矩阵中的不可靠部分会将式(6)中数据b所包含的噪声进行放大,导致结果出现较大偏差。Tikhonov正则化通过引入滤子函数对矩阵的奇异值进行修正,在修正不可靠部分的小奇异值过程中也不可避免地将可靠部分的大奇异值进行变换,导致反演结果对噪声数据较为敏感,稳定性较差;TSVD正则化通过将矩阵不可靠部分也就是奇异值矩阵中的小奇异值部分进行完全截断,在消除矩阵不可靠部分中对噪声放大部分的同时造成不可靠部分中所含信息的缺失,降低了解的准确性[14-15]。 在对Tikhonov正则化和TSVD正则化两种算法进行综合考虑后,结合这两种算法的优点,通过设定不同的阈值将矩阵按照大奇异值、小奇异值以及剩余奇异值分成非常可靠部分、不确定部分以及非常不可靠部分,让滤子函数仅对中间不确定部分进行修正调整,对非常可靠部分不做变化,并将非常不可靠部分进行完全截断,以期实现在保留不可靠部分细节性信息的同时降低其中非常不可靠成分对噪声的放大作用。 Tikhonov正则化算法的滤子函数是: (10) 根据滤子函数式(10)及选取的正则参数,可求得解为: (11) TSVD正则化算法的滤子函数是: (12) 根据滤子函数式(11)及其选取的截断正则参数,可求得解为: (13) 由式(11)与(13)可以看出,Tikhonov正则化会将所有矩阵的所有奇异值均进行变化,在保留小奇异修正值的同时也将大奇异值进行了变化;而TSVD正则化是直接将其所认定的小奇异值进行了完全截断,导致数值模型的部分信息缺失。 改进的正则化算法TTSVD的滤子函数是: (14) 式中,k代表非常可靠部分的设定阈值,其值为截断奇异值的序列号;λ为选取的正则化参数,t代表的是不确定部分的设定阈值,其值是根据正则化参数λ和截断奇异值序列号k来确定的。当正则化参数为λ时,奇异值序列中必定存在一个与之相近的奇异值σλ1满足以下条件: (15) t是以奇异值σλ1的序列号λ1为中心,从λ1向右扩充截断参数k后的奇异值总数,即: t=λ1+k。 (16) 根据滤子函数式(14)及其选取的参数k和t,可求得解为: (17) 在以上三种求解算法中,均需要确定正则化参数,本研究采用应用广泛的L曲线法进行选取。 为了更全面地展现并研究TTSVD算法对于动态光散射噪声数据反演结果的影响,本研究通过建立模拟动态光散射含噪数据来代替实际观测数据进行全面分析。在实际颗粒粒度检测过程中,样品的杂质与浓度情况、实验温度的变化、光电倍增管的背景杂散光等诸多因素的存在,会使得实际观测数据中包含大量由不同因素所导致的随机噪声。依据中心极限定理思想,通过以正态分布白噪声对模拟的无噪数据进行激励,让模拟产生的观测数据能够达到与真实结果较为接近的效果。具体模拟实现过程:首先通过模型分别建立单峰窄分布颗粒系、单峰宽分布颗粒系、双峰窄分布颗粒系、双峰宽分布颗粒系四种不同的粒度分布函数作为模拟的真实颗粒粒度分布结果,然后通过公式分别得到其自相关函数数据,也就是在颗粒粒度检测过程中所得到的不含噪声污染的理论观测数据,最后在相关函数数据中分别加入不同强度水平的正态分布白噪声,得到噪声干扰下的实际观测数据来进行研究。 模拟实验中,使用Johnson’s SB[19]分布作为模拟粒径分布模型(即真实粒度分布),其表达式是: (18) 式中,t=(d-dmin)/(dmax-dmin)是粒径大小归一化的结果,dmax和dmin分别是模拟粒度分布中粒子的最大粒径和最小粒径;u和δ表示模型的分布参数,这两个参数值将决定模拟的粒度分布情况。模拟实验参数分别为:温度25 ℃,分散介质(水)的折射率1.331,入射光的波长632.8 nm,散射角90°,水的黏度系数0.89×10-3N·s/m2,波尔兹曼常数1.380 7×10-23J/K。通过对自相关函数g(τ)添加不同水平的正态分布白噪声,来模拟在实际测量过程中可能出现的不同程度的干扰情况。 为了能够更直观地展示算法对模拟反演结果的影响,将新算法所得的结果与传统的Tikhonov正则化、TSVD正则化结果进行对比,同时引入峰值粒径(peak particle size,PPS)、峰值相对误差(peak particle size relative error,PPSRE)、粒度分布误差(particle size distribution error,PSDE)三个重要指标参数并以数据形式展现出来。其中峰值粒径指的是粒度分布峰值点所对应的粒径值,峰值相对误差指的是算法求取峰值与模拟峰值的相对误差大小 RPPSRE=(|dpps_inv-dpps_true|/dpps_true)×100%。 (19) 其中,dpps_inv和dpps_true分别代表算法峰值粒径和模拟峰值粒径。粒度分布误差指的是算法求取的粒度分布与模拟的粒度分布之间的误差: (20) 其中,xpps_inv和xpps_true分别代表算法求取的粒度分布和模拟的粒度分布。 3.2.1 单峰颗粒系的反演结果与数据对比 单峰窄分布颗粒系对应的模拟参数为:u=3.8,sigma=2.0,dmin=1,dmax=800;单峰宽分布对应的模拟参数为:u=0.8,sigma=1.8,dmin=1,dmax=800。两种单峰分布颗粒系的的反演结果和数据如图1~2以及表1~2所示。 图1 单峰窄分布颗粒系在不同噪声强度下的反演结果Fig.1 Inversion results of unimodal narrow distribution particles under different noise intensities 由图1(a)与表1数据所示,对于在噪声强度为0.000 1时的单峰窄分布颗粒系,TTSVD算法和TSVD算法均能反演出与真实结果相同的PPS,比Tikhonov算法的结果更精确;同时,TTSVD结果的PSDE比Tikhonov的低0.001 2,比TSVD低0.000 1。这也就是说,在低噪声的情况下TTSVD所选取的可靠部分加上不确定部分已经近似替代了原矩阵,使得TTSVD反演结果与真实结果之间的拟合程度更优于其他两种算法;而非常不可靠部分的截断使得修正后的矩阵获得比Tikhonov更精确的结果。同样的,对于单峰宽分布颗粒系也印证了这一解释。如图2(a)所示,在噪声为0.000 1时的单宽峰颗粒系,TTSVD的PPSRE比Tikhonov低3.35%、比TSVD低0.67%;在PSDE方面,TTSVD结果也表现出与单窄峰颗粒系相类似的情况。这也说明对选取的不确定部分进行修正以及对非常可靠部分保持不变的处理是非常有必要的,优化了反演的精度以及平滑性。 图2 单峰宽分布颗粒系在不同噪声强度下的反演结果Fig.2 Inversion results of unimodal wide distribution particles under different noise intensities 表1 单峰窄分布颗粒系在不同噪声强度下的反演数据Tab.1 Inversion data of unimodal narrow distribution particles under different noise intensities 表2 单峰宽分布颗粒系在不同噪声强度下的反演数据Tab.2 Inversion data of unimodal wide distribution particles under different noise intensities 如图1和图2(b)、2(c)所示,随着噪声强度不断增强,三种算法的结果均出现了不同程度的变化,其中以Tikhonov算法受噪声的干扰最为严重,而TTSVD和TSVD算法受噪声干扰的影响相对较小。相较于Tikhonov算法,随着噪声的不断增强,TTSVD的PPSRE相较真实值变化不大,而Tikhonov算法的PPSRE也随着噪声强度增强而变大,在噪声强度为0.010 0时,两种算法的单宽峰颗粒系峰值粒径相对误差达到4.36%,单窄峰颗粒系峰值粒径相对误差达到5.62%。,Tikhonov算法已经不能得到准确的PPS。这说明,相较于将奇异值完全修正的Tikhonov算法,TTSVD的部分截断与部分修正是完全有必要的。相较于TSVD算法,TTSVD和TSVD的PPSRE相差不大,且在单宽峰分布颗粒系TTSVD结果的PPSRE要优于TSVD结果,在噪声强度为0.010 0时,单宽峰颗粒系TTSVD算法的PPSRE要比TSVD的低5%;与此同时,不管噪声强度如何变化,TTSVD算法的PSDE始终保持着比TSVD算法更低的值。这是由于TTSVD算法在截断非常不可靠部分的小奇异值后,相较于Tikhonov算法受噪声的扰动影响变小;确定部分的完全保留与不确定部分的修正,使得TTSVD算法能够具有比Tikhonov和TSVD算法更低的PSDE,提高了Tikhonov、TSVD算法与真实结果的拟合度。 综上所述,改进的TTSVD算法能够在单峰分布颗粒系的反演中得到比较精确且稳定的结果。相较于Tikhonov算法,TTSVD具有更好的抗噪性与精确性,特别是噪声强度为0.010 0时,峰值误差至少降低了3%,粒度分布结果也更接近真实粒度分布情况;相较于TSVD算法,TTSVD算法反演结果具有更高的拟合度,在低噪声的情况下具有更好的精确性。 3.2.2 双峰颗粒系的反演结果与数据对比 本实验中双峰颗粒系是由两种单峰颗粒系按照1∶1的光强比进行混合而成,双峰窄分布对应的模拟系数为:u1=4.9,sigma1=3.1,u2=-3.9,sigma2=4.0,dmin=1,dmax=800;双峰宽分布颗粒系对应的模拟系数为:u1=3.0,sigma1=2.1,u2=-2.1,sigma2=2.2,dmin=1,dmax=800。两种由不同颗粒系混合而成的双峰分布颗粒系反演结果和数据如图3~4以及表3~4所示。 图3 双峰窄分布颗粒系在不同噪声强度下的反演结果Fig.3 Inversion results of bimodal narrow distribution particles under different noise intensities 表3 双峰窄分布颗粒系在不同噪声强度下的反演数据Tab.3 Inversion data of bimodal narrow distribution particles under different noise intensities 如图3和图4(a)所示,在噪声强度为0.000 1时,三种算法均能得到比较精准的双峰颗粒系的峰值粒径,其中又以TTSVD算法结果的PPSRE最小,拟合效果最好。由表3数据可知,在双窄峰颗粒系中三种算法得到的第一个峰值粒径完全一样,在第二个峰值上TTSVD和TSVD算法比Tikhonov算法的PPSRE低0.85%;根据表4数据,TTSVD算法在双宽峰颗粒系的PPSRE比TSVD算法低0.5%左右,比Tikhonov算法低1.5%~5.8%。这说明,在外部噪声较小的情况下,TTSVD算法和TSVD算法对非常可靠部分奇异值的保留是很有必要的,提高了反演的精度。从粒度分布反演误差PSDE的角度以及图像双峰的分辨率来看,宽峰颗粒系和窄峰颗粒系的规律基本一致,TTSVD算法结果的粒度分布误差均低于TSVD和Tikhonov算法,与真实结果的拟合度较高,能够较好地反映真实结果的粒度分布情况。 图4 双峰宽分布颗粒系在不同噪声强度下的反演结果Fig.4 Inversion results of bimodal wide distribution particles under different noise intensities 表4 双峰宽分布颗粒系在不同噪声强度下的反演数据Tab.4 Inversion data of bimodal wide distribution particles under different noise intensities 如图3和图4(b)、4(c)所示,随着噪声强度的不断增强,三种算法对颗粒粒度反演的结果不断变差,特别是在噪声强度为0.010 0时,三种算法已经基本失去了第二种颗粒系的分布情况。相比较而言,TTSVD算法具有比Tikhonov算法和TSVD算法更好的结果。如图3(b)所示,在噪声强度为0.001 0时,TSVD算法反演结果在第一个颗粒系上的峰值准确性要优于TTSVD和Tikhonov算法,但其同时也丢失掉第二颗粒系信息;而TTSVD算法能够同Tikhonov算法一样获取第二个峰的颗粒信息,且得到了比Tikhonov算法在第一峰值PPSRE上低1.54%、第二峰值上低5.63%的反演结果。与之相类似的是,在图4(b)中,Tikhonov算法在0.001 0噪声时取得了较噪声强度0.000 1时更好的结果。出现这种情况均是因为施加噪声随机性较大以及L曲线选取的参数未能达到最优从而导致Tikhonov和TTSVD算法反演结果受到影响,但与Tikhonov算法不同的是,TTSVD对非常不可靠部分奇异值的截断处理使得该算法能够取得比Tikhonov算法更好的结果,进一步说明TTSVD算法对非常不确定部分奇异值的截断处理是很有必要的。如图3和图4(c)所示,在噪声强度为0.010 0时,TTSVD算法得到的第一个峰值颗粒系结果比Tikhonov和TSVD算法更准确,同时在双窄峰颗粒系上,能够分辨出第二个颗粒系的存在情况。造成这种结果的原因是TSVD将不确定部分与不可靠部分的奇异值进行了截断,使得在反演中缺失部分有效数据,随着噪声强度增加截断的奇异值就越多,所保留的有效信息也就越少,最终导致反演结果在高噪声情况下失去第二种颗粒系的粒度分布情况;Tikhonov正则化算法虽然保留了大量有效信息,但是其滤子函数对矩阵数学模型中大小奇异值的处理不充分,使得小奇异值对噪声变化非常敏感,大奇异值的变化使得结果对可用信息的处理效率降低。而TTSVD算法将小奇异值部分进行划分并分别处理,在尽可能保留有效信息的同时,降低了小奇异值对噪声的放大作用,在一定程度上对Tikhonov和TSVD算法进行了优化。 综合上述分析得出:改进的TTSVD算法具有比TSVD算法、Tikhonov算法与原颗粒粒度分布更高的拟合度,对双峰颗粒系的反演能够得到比TSVD算法与Tikhonov算法更好的结果。TTSVD算法在低噪声的情况下反演得到的结果精确度要高于TSVD算法与Tikhonov算法;在高噪声的情况下,具有比Tikhonov算法更强的抗噪性、比TSVD算法更好的双峰分辨率。 为验证该算法在颗粒粒度检测应用中的有效性,使用DLS实验装置获取nm单峰分布的标准聚苯乙烯颗粒相关函数数据并进行反演验证。DLS装置主要由波长为532 nm的绿色激光器、端窗式光电倍增管以及128通道的高速数字相关器组成,测试实验温度为27℃,散射角为90°,分散介质选择纯净水。根据动态光散射技术理论可知,该技术通过采用相关去噪法对获取的光强信号进行去噪,去噪效果与测量时间成正相关,测量时间越长去噪效果越好。而测量时间是采样时间与数据长度的乘积,这就要求实验检测时的数据量越大越好。为了得到不同程度噪声情况下的观测数据,在采样数约为2×106和2×105时分别获取相关函数数据作为低噪声与高噪声下的观测数据,并以TSVD、Tikhonov和TTSVD算法分别对实验数据进行反演,结果和数据如图5和表5所示。 由图5和表5可以看出,在采样数量为2×106时,三种算法均能比较准确地反演出颗粒的峰值粒径情况,其中Tikhonov算法结果的峰值误差为0.41%,粒度分布较宽;TTSVD和TSVD算法结果的峰值误差为0.21%,粒度分布较窄。相较于采样数量为2×106时的反演结果,在采样数量为2×105时,TTSVD和TSVD算法仍能够比较准确地反演出颗粒粒径峰值结果,其中TTSVD算法结果的峰值误差保持不变,TSVD算法结果的峰值误差增大到0.47%,而Tikhonov算法结果的粒径峰值出现较大变化,峰值误差增大5.65%。因此,TTSVD算法能够更好反演出实际的颗粒粒度分布结果,验证了模拟数据的结论。 图5 350 nm颗粒在不同采样数量下的反演结果Fig.5 Inversion results of 350 nm particles under different sampling numbers 表5 350 nm颗粒在不同采样数量下的反演数据Tab.5 Inversion data of 350 nm particles under different sampling numbers 在动态光散射数据的反演实验的基础上,结合Tikhonov正则化算法和TSVD正则化算法,提出一种将奇异值序列进行区域划分并分别处理的改进正则化方法TTSVD。将奇异值序列划分为非常可靠部分、不确定部分以及非常不确定三部分,对三部分以不同的滤子函数进行处理,解决了Tikhonov算法对所有奇异值进行修正以及TSVD算法将所有小奇异值进行完全截断的缺陷。通过将原始颗粒粒度分布作为基准,以改进的正则化方法TTSVD和Tikhonov、TSVD算法分别在强度为0.000 1、0.001 0、0.010 0下的DLS数据反演进行结果比对,确定新算法结果能够有较强的抗噪性、较好的精确性以及与真实结果之间更好的拟合性。当然由于计算存在随机性,可能偶尔会出现其他方法某个参数更好的情况,但总体而言,TTSVD方法是一种可行的颗粒粒度反演方法。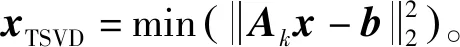
2 新正则化算法TTSVD
3 模拟实验分析
3.1 模拟实验及参数设定
3.2 结果对比与数据分析




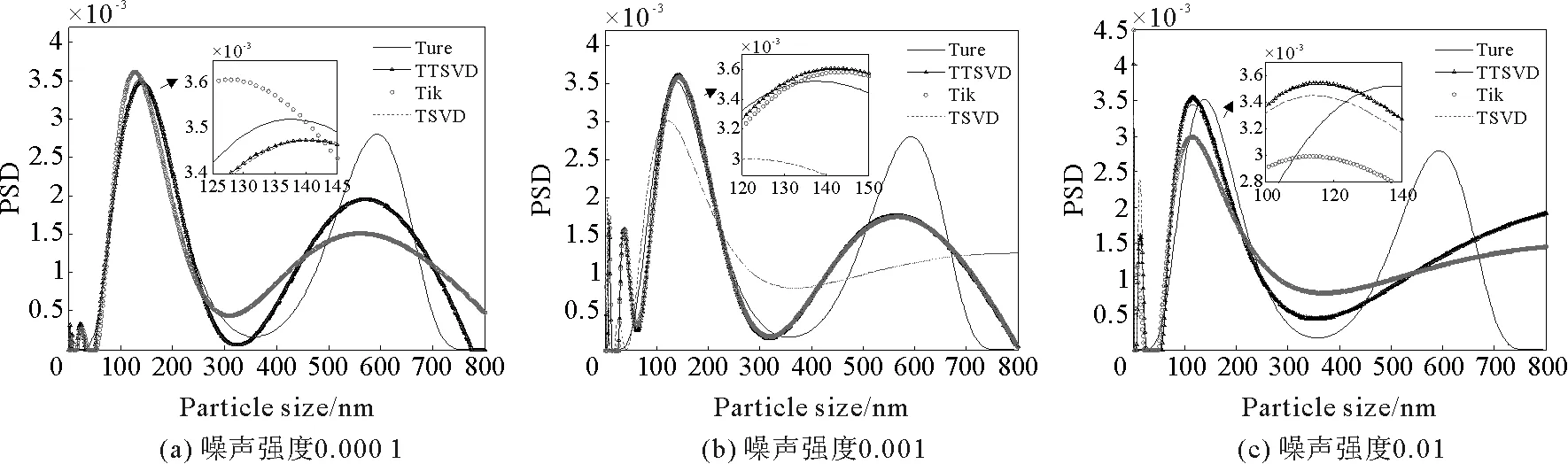
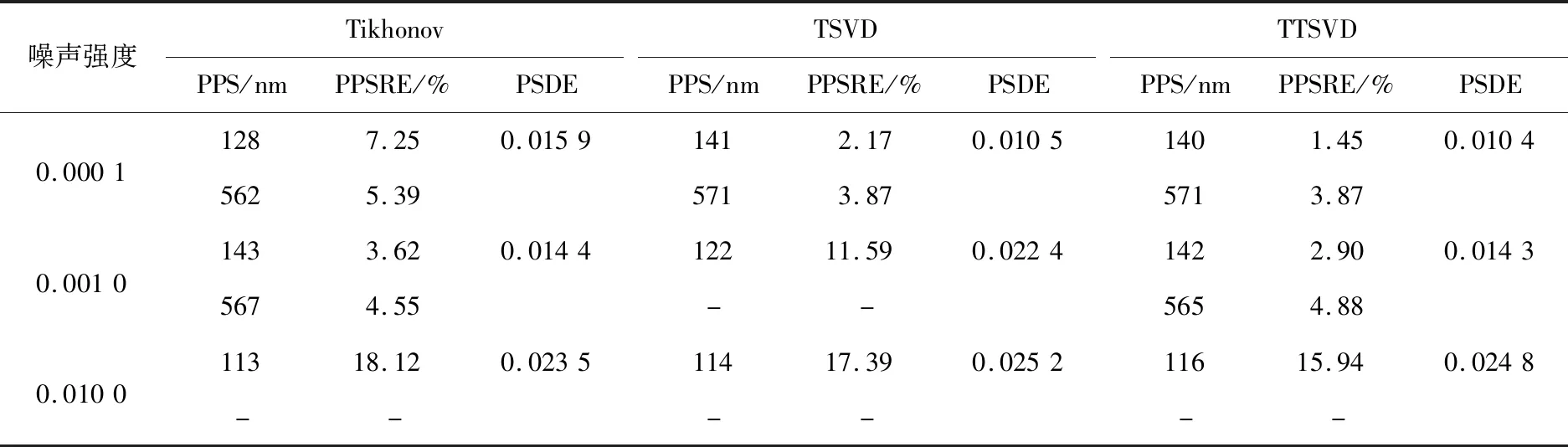
4 实验数据的反演分析
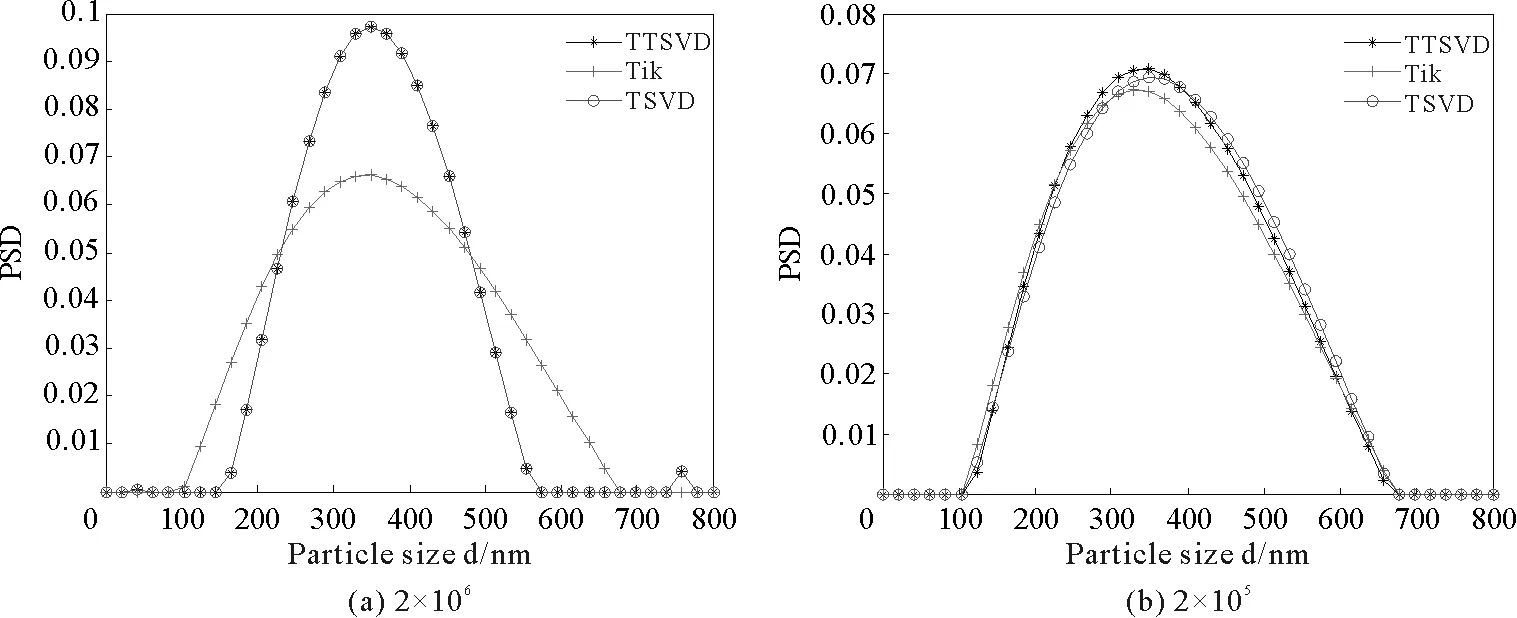

5 结论

