基于自适应分段聚合的云模型序列相似度评价方法
李 金 武
(郑州科技学院信息工程学院 河南 郑州 450064)
0 引 言
时间序列是一种具有高维特性,且与时间相关的连续型指标数据,广泛存在于金融、气象、交通和网络安全等领域。如何从时间序列数据中挖据有价值的信息和知识为决策者提供有效的决策支持,是数据挖掘技术研究的方向之一[1-2]。如何对时间序列数据进行有效的约简和降维,是数据挖掘的首要任务。
目前常用的数据降维技术有离散傅里叶变换(DFT)、离散小波变换(DWT)、分段线性表示(PLR)和分段聚合近似(PAA)等[3]。DFT能够保留数据的全局特性,但是忽略了数据的局部特征,且只能应用于平稳序列;DWT虽然可以提取和分析数据的局部特征,但只能应用于长度为2的整次幂的时间序列;PLR是用直线段来近似表示时间序列的局部波动,是一种较好的数据压缩方法,但转折点的提取是关键;PAA将时间序列平均分割成多段,每段用段内平均值表示,但子段宽度的确定并不具有普适性,且对于波动剧烈的时间序列,会严重丢失数据局部细节。
依据时间序列连续型指标数据的自身特性,提出一种自适应分段聚合云模型评价方法,利用云模型的熵评价分段序列稳定性,动态识别时间序列数据特征并用云模型表示,同时基于云模型的距离和形状,给出云模型相似度评价方法,对聚合后的时间序列关系进行评价度量。
1 云模型及分段聚合理论
1.1 云模型理论
云模型是处理定性概念与定量描述的不确定性转换模型,反映了知识表达中模糊性与随机性之间的关联性,自李德毅院士1995年提出至今,云模型已经在数据挖掘[4]、自然语言处理[5]、安全评估[6]和决策分析[7-8]等领域得到应用,并取得良好效果。下面给出云模型相关概念。
定义1设U是用精确数值表示的定量论域,C是论域上的定性描述,对于x∈U,且x是C上的一次随机实现,则x对于C的确定度y=yc(x)∈[0,1]是一个具有稳定倾向的随机数,把(x,y)在论域U上的分布称为云[9]。
定义2用3个参量(Ex,En,He)表示云的数字特征的过程,称为云模型,记作C(Ex,En,He)。Ex表示云模型的期望,是最能够代表定性概念的点;En表示云模型的熵,反映了定性概念的模糊性和随机性;He表示云模型的超熵,是云模型熵的不确定性度量,直接反映了云模型的厚度。
定义3对于任意云滴变量x,x满足x~N(Ex,En′2),且En′~N(En,He2),存在一条曲线贯穿整个云滴集合,描述了云的整体几何形态,这条曲线称为云期望曲线,记作y(x),y(x)解析式如下:
y(x)=exp[-(x-Ex)2/2En2]
(1)
定义4通过云的数字特征(Ex,En,He)产生n个云滴,实现定性概念到定量数据转换的过程,称为正向云发生器,记作cloud(Ex,En,He,n)。
定义5将一定数量的云滴x,且x∈X,转换为某一定性概念,即实现定量数据到定性概念转换的过程,称为逆向云发生器,记作back_cloud(X)。
1.2 分段聚合理论

(2)

2 云模型分段聚合及评价方法
为了更好地对时间序列连续型指标进行评价,考虑连续型指标数据的局部特性,提出一种自适应分段聚合云模型评价方法。首先依据云模型的熵判断分段聚合数据的稳定性,自适应地形成稳定性较好的云模型数据序列,其次给出云模型数据序列的相似度计算方法,对两个时间段内同一连续型指标进行近似评价。
2.1 云模型自适应分段聚合
云模型自适应分段聚合是依据云模型的熵对数据进行可变长度的分段处理,打破传统平均分割数据的处理方法,从而最大限度提取数据特征值,实现数据从高维到低维的不确定性转换。首先利用逆向云发生器依次对当前分段数据进行云模型描述,得到各分段数据云模型数字特征,然后比较各分段数据云模型的熵,找到熵值最大的云模型所对应的原始分段数据,对这个原始分段数据再次进行云模型划分。
在进行云模型划分时,为了尽可能保留原始分段数据局部特征,需对其进行遍历,找到关键点,对关键点前后两段数据分别进行云模型描述,从而把熵值最大的云模型划分为两个新的云模型,确保被划分云模型熵与新划分的两个云模型熵之和差值最大。
根据云模型分段聚合思想,设计云模型分段聚合算法,如算法1所示。
算法1云模型分段聚合算法
输入:n维时间序列数据TD={td1,td2,…,tdn},聚合后的维度m。
输出:m维云模型数据序列CD={cd1,cd2,…,cdm},cdi=[Exi,Eni,Hei]。
Step1利用逆向云发生器,对分段聚合数据进行预处理,提取数据特征值,用矩阵Vm×5记录这些信息。其中:V(i,1∶3)表示第i个子序列云模型特征值[Exi,Eni,Hei];V(i,4∶5)表示第i个子序列在原时间序列中的始末位置[tf,tb]。初始设置i=1,V(i,1∶3)=back_cloud(TD),V(i,4∶5)=[1,n]。
Step2若i>m,则程序结束,输出CD,否则执行Step 3。
Step3对当前矩阵Vi×5第二列V(1∶i,2)进行检索,查找最大熵值,表示为V(i0,2),1≤i0≤i。其中最大熵值的索引号为i0,即第i0个子序列的云模型熵值最大。
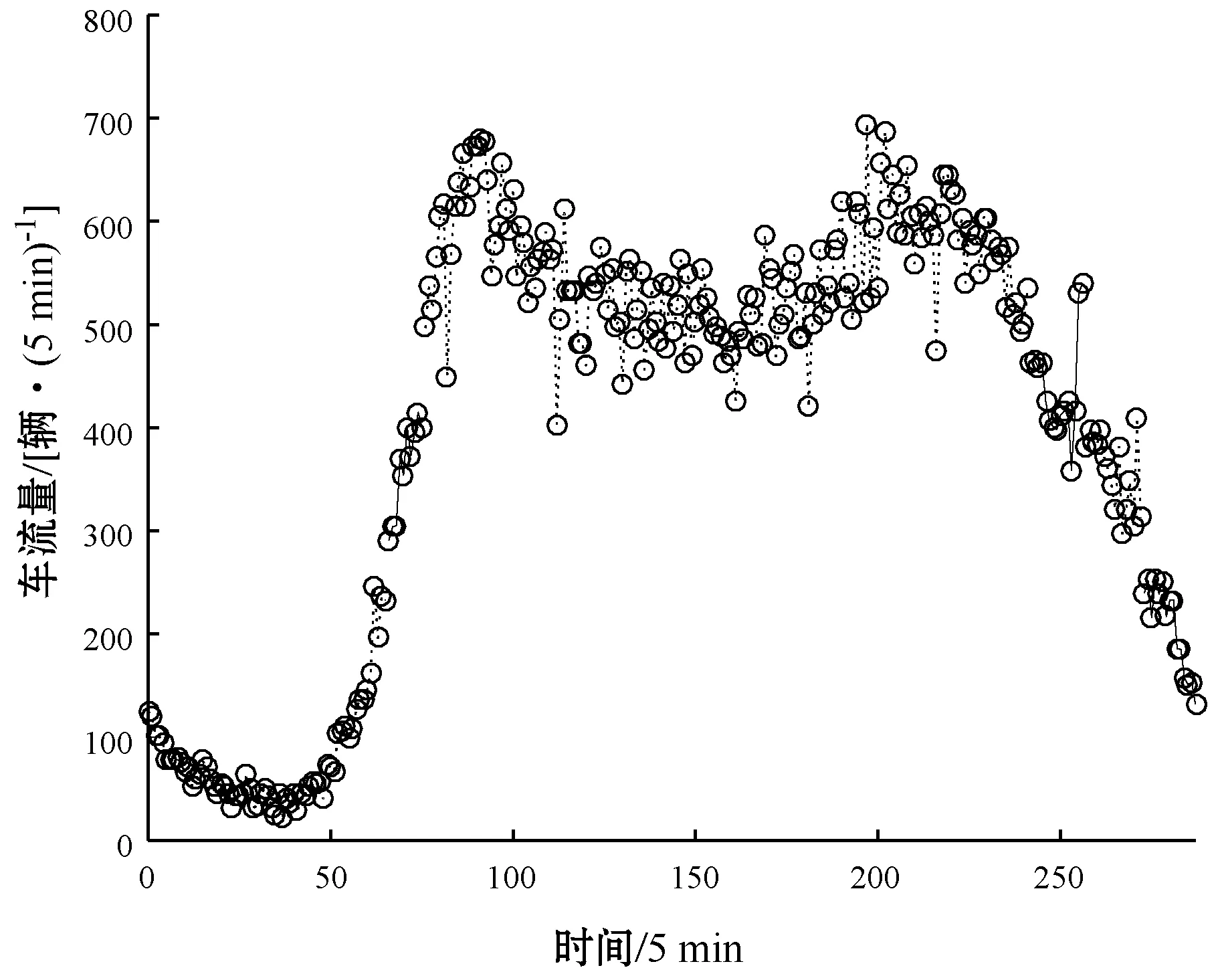
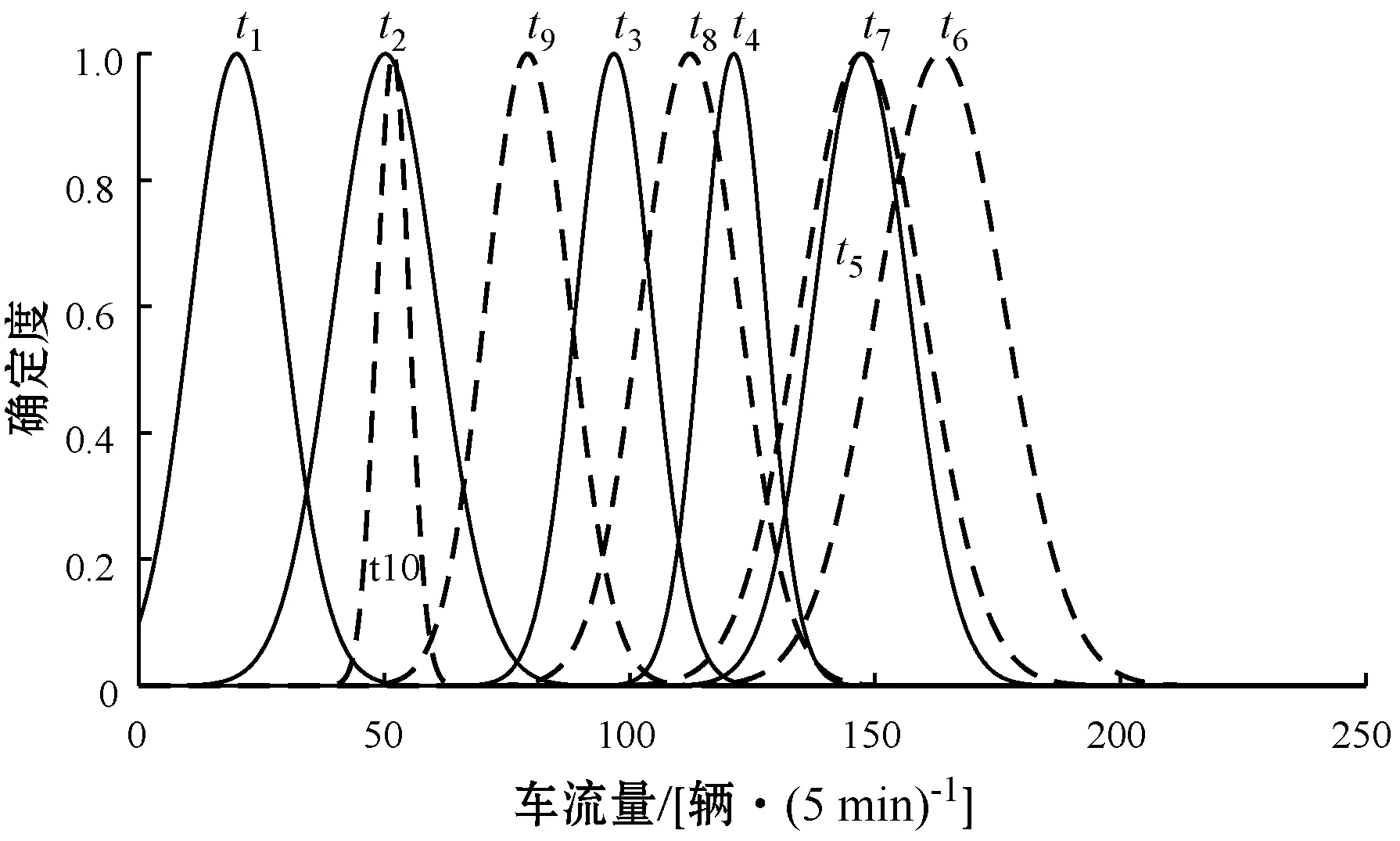
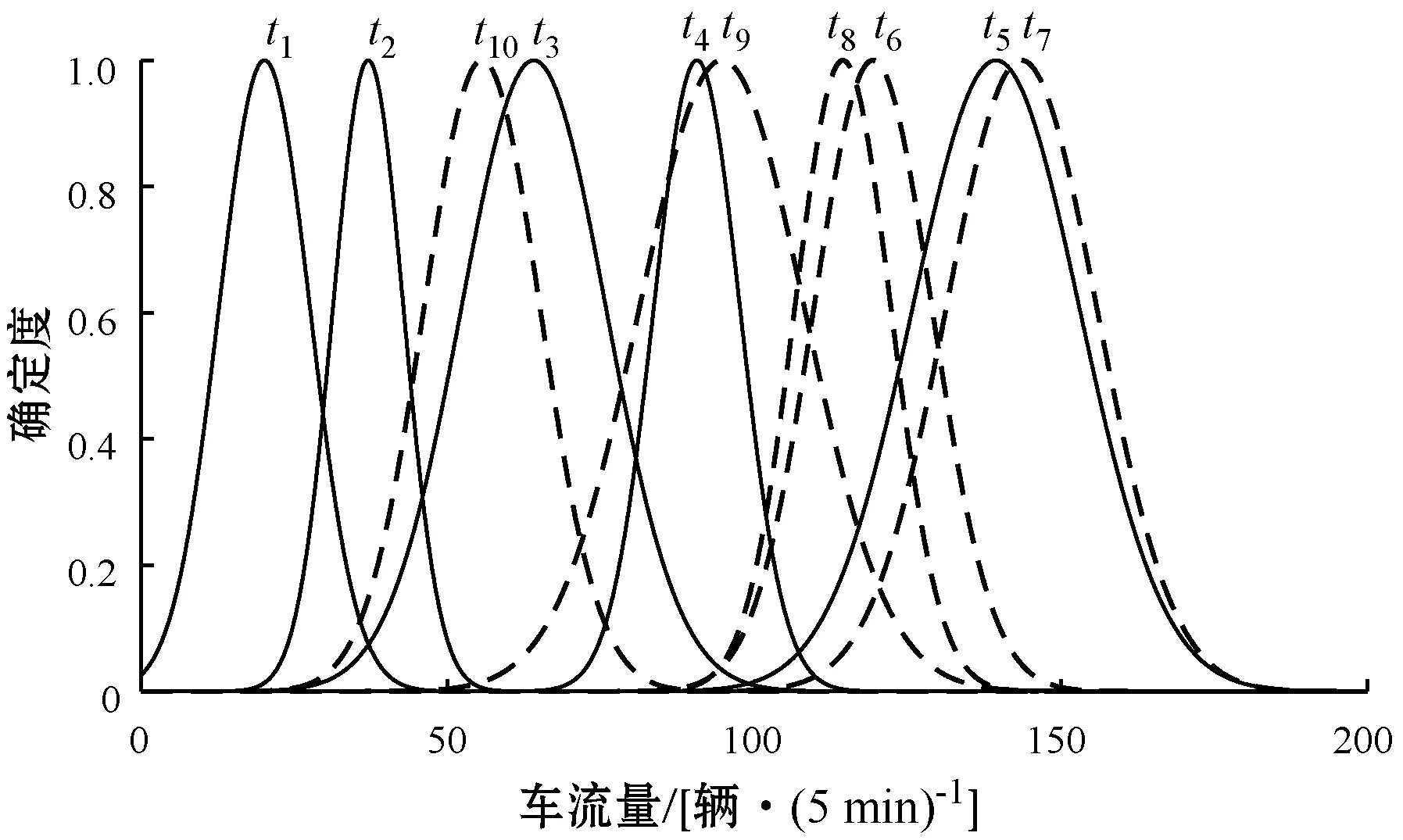
Step4对当前第i0个子序列进行分段,分为两段。提取第i0个子序列的始末位置信息,令t1=V(i0,4),t2=V(i0,5),记第i0个子序列为TD(t1∶t2)。从子序列TD(t1∶t2)中搜索t0,t1 循环遍历t0,通过计算使得ΔEn最大。 L(1∶5)=[back_cloud(TD(t1∶t0)),t1,t0] R(1∶5)=[back_cloud(TD(t0∶t2)),t0,t2] ΔEn=V(i0,2)(t2-t1)-[L(2)(t0-t1)+R(2)(t2-t0)] Step5记V(i0,1∶5)=L,V(i0+1,1∶5)=R,i=i+1,返回Step 2。 对于降维后的云模型数据序列,需要利用云相似度评价方法来衡量两个云模型之间的近似程度。由于正态云的期望曲线能够较好地反映云模型的数字特征,综合考虑云模型的形状和距离,可以使用云模型期望曲线相交面积来计算相似度,在此特意把两个云相交的面积提升至更高层面进行间接计算,充分体现云模型亦此亦彼的特性。 2.2.1云交点判定规则及“与”区域面积计算 两个云相交的面积称之为“与”区域面积,要计算其面积,首先要判定云期望曲线交点,云模型特征值直接影响交点个数和位置。设云模型Ci(Exi,Eni,Hei),i=1,2,yi(x)为云期望曲线,根据定义3,联立云期望曲线组成的方程组,可求两个云的交点。 (3) 在此可以不考虑云模型“3En”规则[11],依据式(3)求得交点主要表现为以下几种情况: (1)Ex1≠Ex2,En1=En2,求得单交点p,如图1(a)所示。 p=(Ex1En2+Ex2En1)/(En1+En2) (2)Ex1=Ex2,En1≠En2,求得单交点p,如图1(b)所示。 p=(Ex1En2+Ex2En1)/(En1+En2)=Ex1=Ex2 (3)Ex1 (4)Ex1=Ex2,En1=En2,两条云期望曲线重合,在此不考虑云交点,如图1(d)所示。 (a) Ex1≠Ex2,En1=En2 (b) Ex1=Ex2,En1≠En2 (c) Ex1≠Ex2,En1≠En2 (d) Ex1=Ex2,En1=En2图1 云交点及”与”区域面积图 令“与”区域面积为S∩,其计算方法可以通过积分求得,云的位置关系不同,S∩的求法也不尽相同,在此先根据云交点判定规则确定交点,S∩主要有以下几种不同的情况: (1) 存在双交点p1、p2,不妨设p1 代入云期望曲线: 考虑到被积函数不可积,对其变形为标准正态分布函数求积分,进行变量换元代换,令u=(x-Ex1)/En1,v=(x-Ex2)/En2,dx=En1·du=En2·dv。 令Φ(·)为标准正态分布概率分布函数,其值可以通过查表求得,则S∩变形为: (2) 存在单交点p,如图1(a)所示,S∩由两部分组成。 进行变量换元代换,令u=(x-Ex2)/En2,v=(x-Ex1)/En1,dx=En2·du=En1·dv,Φ(·)为标准正态分布概率分布函数,S∩变形为: (3) 存在云重合或包含关系,如图1(b)和图1(d)所示,S∩只有一部分,且由较小云(若云重合,选其中任何一个)进行积分求得。 进行变量换元代换,令u=(x-Ex2)/En2,dx=En2·du,S∩变形为: 2.2.2综合云生成规则及云相似度评价方法 综合云[12]是两个基础云在更高层面的不确定性表示,它包含低层次概念的全部信息,由此可以利用基础云的截断熵计算综合云。把截断熵作为权重,通过加权求和计算综合云的期望和超熵,而综合云的熵为两个基础云截断熵之和。设基础云Ci(Exi,Eni,Hei),i=1,2,yi(x)为云期望曲线,Li(x)代表论域上两期望曲线最大值,反映交点对期望曲线的分段表示。 把基础云的截断熵作为权值,利用式(4)计算综合云的数字特征,即综合云Cz(Exz,Enz,Hez)。 (4) 基础云与综合云“与”区域面积大小决定了基础云概念对综合云概念的贡献程度,“与”区域面积越大,则对综合云概念的贡献程度越大,此时两个基础云越接近。将基础云和综合云放到同一云图中,如图2所示,y1(x)、y2(x)为基础云期望曲线,yz(x)为综合云期望曲线,p1、p2是y1(x)与yz(x)的交点,p3、p4是y2(x)与yz(x)的交点,设待评价基础云Ci与综合云Cz“与”区域面积分别为S∩1和S∩2,综合云与横轴所围面积为Sz。 图2 基础云与综合云位置关系 S∩1和S∩2可以通过2.2.1节方法求得,Sz通过积分求得。 进行变量换元代换,令u=(x-Exz)/Enz,dx=Enz·du,S2变形为: 综合考虑基础云对综合云的贡献程度,定义两个基础云的相似度为: (5) 式(5)是基于云期望曲线“与”面积确定的云相似度,仅从距离上考虑云模型的相似性,忽略云模型形状,在此提出一种通过云模型超熵进行修正的相似性度量方法,兼顾云模型的距离和形状,对式(5)进行修正,修正后的相似度为: s(C1,C2)sxz(C1,C2)∈[0,1] (6) 如果给定两个n维时间序列数据S和R,通过2.1节方法进行云模型分段聚合,降维以后得到两个m维云模型数据序列SC和RC,定义两个云模型数据序列的相似度TDS。 TDS(SC,RC)∈[0,1] (7) 为了更好地验证评价方法的有效性,采用实际的交通流调查数据,对2018年9月10号某条道路一天的交通流进行分析,本条道路分为4车道,主要从两个方面进行分析,即道路交通流的分段聚合效果和车道交通流的相似度。数据集含有5个交通流时间序列,即Lane 1(1车道)、Lane 2(2车道)、Lane 3(3车道)、Lane 4(4车道)和Lane #(#道路),其中Lane #为全部4车道的车流量之和,从0:00到23:55每隔5分钟记录一次车流量变化情况,即每个交通流时间序列有288个车流量状态数据,车流量如图3所示。 图3 车流量变化 利用云模型分段聚合方法,可以自适应地对交通流数据进行特征识别和表示,把具有相同特征的交通流数据划分为一段,并用云模型表示。通过Lane#交通流分析分段聚合效果,对交通流数据进行10维和6维的云模型分段聚合处理,处理结果如表1和表2所示,其中(t0,t1)表示t0到t1的数据聚合为一段。 表1 Lane #分段聚合及云模型特征-10维 表2 Lane #分段聚合及云模型特征- 6维 依据表1和表2的分段序列,对Lane#交通流数据进行分段,分段效果如图4和图5所示,时间维度波动较小的数据,即数据特征近似的会被自动划分为一段,有利于下一步从时间维度上进行数据相似度的评价。从6维到10维的分段聚合过程来看,随着分段维度的增大,能够根据数据特征的近似性自动进行分段,最大限度保持时间维度上数据的局部特征。 图4 分段聚合效果-10维 图5 分段聚合效果- 6维 在时间维度上对云模型序列进行相似度分析,首先需对原始数据进行分段聚合并用云模型表示。在此,对4个车道交通流数据依次进行分段聚合,得到4个10维的云模型序列,聚合后的云模型特征见表3-表6。 表4 Lane 2交通流云模型特征 表5 Lane 3交通流云模型特征 表6 Lane 4交通流云模型特征 依据表3-表6的云模型数字特征,得到云模型曲线如图6所示,(a)-(d)依次为4个车道交通流云模型曲线,在时间维度上表现为10个云,用ti表示第i个时间片的云模型描述,1≤i≤10。 (a) Lane 1 (b) Lane 2 (c) Lane 3 (d) Lane 4图6 交通流聚合云模型曲线-10维 利用TDS算法,在时间维度上计算云模型序列相似度,如表7所示。Lane 2与Lane 4全天车流量相似度为0.715 6,相似度最高;Lane 1与Lane 3全天车流量相似度为0.608 9,相似度最低,即交通流变化特性较之其他车道差异性较大。 表7 TDS算法计算相似度 本文提出时间序列云模型相似度评价方法,利用云模型的熵来判断分段子序列的稳定性,自适应地对时间序列进行分段聚合。同时给出TDS相似度评价算法,该算法把云模型相似度评价提升至更高层面,基于云期望曲线的相交面积进行评价,并且通过云模型的超熵对相似度进行修正,充分体现云模型亦此亦彼的特性,是对不确定性问题的一种新探索。实验结果表明,该方法较之经典聚合近似PAA,具有更好的聚合效果,同时在时间维度上进行的相似度评价更符合现实情况,特别是对于随机性和突发性较强的数据序列,效果会更加明显。然而如何降低算法复杂度,如何确定分段聚合的维度,是今后研究需要进一步探讨的问题。2.2 云模型时间序列评价方法








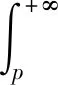





3 实验仿真

3.1 分段聚合效果分析



3.2 云模型序列相似度分析






4 结 语

