面向远程实验设备的最优资源调度方法

孙 博 俞武嘉 刘光宇

(杭州电子科技大学自动化学院 浙江 杭州 310018)

0 引 言

随着数字孪生技术与高校实验室资源的结合，远程共享使用实验设备有了新的发展思路。实验教学作为课堂理论知识的具体化、实践化，是高校教学环境中的重要一环，实验课程的合理安排，关系到实验室日常工作的顺利进行[1]。因此，如何合理地分配有限实验设备资源并给出最优排课方案成为了新的问题。

目前，实验室设备的调度研究大多聚焦于实验室本身的设备预约和管理[2-3]，或者是实验课程排课和实验室用户之间的关系[4]，缺乏考虑实验室的设备资源调度与高校的实验课程排课之间的协调问题。鉴于此，本文结合高校实验课的排课问题，对高校实验室的远程实验设备调度进行研究。使用改进的遗传算法，将实验课程、实验设备、实验用户与实验时间相匹配，给出合理的实验课排布与设备调度方案，从而实现充分利用实验室资源，提高实验设备的使用率。

1 问题描述与假设

在现实生活中，通常有一类存在能力限制的服务系统S，其限制主要体现在系统拥有的资源R有限；需求发生后，可能由于资源的短缺而需要等待服务，加之需求的特殊性，只有在合适的时间段或者地点才能被服务；需求被满足后离开系统，释放所占用资源。

上述情景延伸到高校的实验课教学中，将多设备信息技术实验室看作一个服务系统，实验室的实验设备是有限的。通常学生以班级为单位在特定的时间做同一个实验，每个班级的任务申请为一个队列。学生在实验课开始后发出实验任务申请，然后实验设备开始工作。某些时候不同班级的学生在同一时刻进行实验课，但实验课程的内容是不一定相同的，实验设备服务不同实验课程的能力也是不同的，远程实验设备调度示意图如图1所示。如果设备的分配不合理，会延迟需求量较高学生的设备资源供应，降低实验课效果；分配过量的设备资源，会造成设备资源的利用率低。实验课结束后，设备资源被释放。

图1 远程实验设备调度示意图

从以上的描述中可以看出,通过先来先服务的规则无法保证实验课的设备使用效率最大化。因此,本文的目标是寻求使实验室远程实验设备效率最大化的设备调度和排课方法。为系统地分析和评价调度安排，本文提出两个假设：(1) 实验产生的服务申请不会消失；(2) 服务申请的到达服从泊松分布。在满足这些假设后，方能构建相应的调度模型，并设计遗传算法寻优。

2 最优化调度模型

通过多设备实验室调度与生产调度的比较，采用生产线调度中常用的三元问题描述方法(α,β,γ)来描述多设备实验课程的调度问题以及最优化模型[5]。实验室的仪器设备资源是有限的，在进行实验课安排前除了要考虑人为因素, 还要考虑设备资源的约束[6]。假设班级c在实验i中需要调用m类设备n台，多个时间条件已经给定，例如：实验开始时间ri、实验处理时间pi，以及实验截止时间di。

采用α描述设备环境：在实验过程中，学生s需要调用m类每类n台设备，所以存在流水车间调度问题；在只有1个班级实验的情况下，存在并行同性能机器调度问题处理；在多个班级同时实验的情况下，存在并行不同性能机器调度问题。综上所述，采用柔性车间作业调度问题将零散的调度问题进行统一处理。

采用β描述实验过程的约束：使用Mi设备作为任务分配的约束，集合Mi表示实验i的可选设备集合，集合Mi不出现，表示实验i可以在任何设备上进行实验；使用优先(偏序)约束作为流水约束，学生s必须等待设备释放，才能继续实验。

采用γ描述实验教学安排的目标：面向实验过程中的设备资源的调用，需要保证不同规格的实验设备根据实验任务分配合理化，将此优化目标定位为负载均衡最优调度问题。在Mi等约束条件下，使用Wj表示单个设备的负载率，采用min max最优化模型来描述：

min max{1-Wj}

(1)

面向实验课在日常教学中的分配，需要保证班级、课程、实验时间，以及根据实验类别调用的实验设备等元素不发生冲突，以时间ti表示各个日常教学中的必要时间，给出时间排序的数学问题：

sequence{t1,t2,t3}

(2)

此外，需要对所有实验设备总使用时间进行优化，以提高设备的利用率：

min{∑Li}

(3)

式中：Li表示单个设备的使用时间。因此，本项目的多个调度问题可以归纳为多目标优化NP-Hard问题。

3 基于遗传算法的调度安排优化

根据上述的调度问题描述以及假设，本文采用遗传算法对实验课程的资源调度进行优化。其中包含远程实验设备和实验用户的分配，以及高校的日常教学中实验课的合理安排。使用下列集合表示这些调度所需因素：

设备集合：S={S1,S2,…,Sn}，在某一个实验课程内，需要N台设备，N≥1。

任务集合：T={T1,T2,…,Tn}，每台客户端发送的服务申请为一个任务Ti。

实验集合：E={E1,E2,…,En}。

班级集合：C={C1,C2,…,Cn}。

专业集合：M={M1,M2,…,Mn}。

课程段集合：P={P1,P2,…,Pn}，Ti表示课程段，例如T1为周一的1～2节课，T2为周一的3～5节课。

时间段集合：W={W1,W2,…,Wn}，Wi表示星期数，例如W1为第一周，W2为第二周。

3.1 编码规则

要实施遗传算法，第一步就是对需要解决的问题进行基因编码。在本系统中，每种基因段采用二进制编码，例如时间段一共是16个，代表16个星期，Wi(i=1,2,…,16)为16个变量。Wi=1表示在第i周有实验课，Wi=0表示第i周没有实验课。根据以上分析，染色体结构如图2所示。

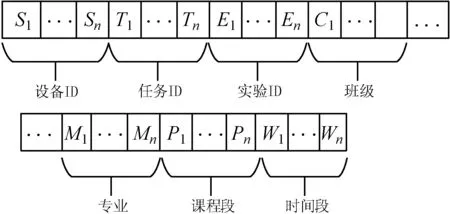
图2 染色体结构示意图

3.2 适应度函数设计

在遗传算法中，遗传的方向需要适应度来决定，适应度表示整个实验课程调度的优秀程度。相对于常见的基于遗传算法的排课算法中的适应度函数设计[7-8]，在实验课程的排课中需要关注设备调度和排课两个部分。因此，在本文适应度函数的设计中，适应度的期望由两个部分组成：实验设备调度和实验课程安排。

(1) 实验设备调度。由上述的调度分析，在一个实验课期间，用户提交任务的过程是相互独立的泊松过程，设备处理任务的过程仍然是泊松过程。那么可以将实验设备的调度抽象成一个M/M/n模型。根据Little公式，系统中平均顾客数量(在上述模型中是客户端发起任务的数量)E(L)与平均逗留时间(在上述模型中是设备的使用时间)E(S)和到达速率λ之间的关系为：

E(L)=λE(S)

(4)

对于M/M/n队列，通过求解生灭过程的稳定概率和应用Little公式，可以得到：

(5)

式中：K是泊松比率函数；n是服务器(上述模型中设备的数量)数量；μ是平均服务速率；ρ是设备利用率，并且：

(6)

通过式(5)和式(6)计算任务平均使用时间和设备利用率。对于线上资源调度合理程度的期望函数公式为：

FUL=t1·E(S)+t2·ρ

(7)

式中：t1和t2用于调控任务平均响应时间和设备资源利用率对线上资源调度合理程度的影响。

(2) 实验课程安排。实验课程安排的合理程度可由两个部分组成：

① 实验课程特征规律。学生逻辑思维活跃的时间段一般在早晨，所以早晨适宜安排理论课程，而且实验课通常需要更长的时间。根据实验课程的特征规律，不同课程段的期望值不同，如表1所示。

表1 实验课程特征规律期望值

对于特征规律的期望函数公式为：

FET=∑FET(i)

(8)

② 教学规划适宜度。在高校教学中，实验课的安排应分布于学期中间。因为学期开始时，学生处于放假归来的状态，此时教学效果并不是很好；而在学期末和期中考试前，学生面临考试周主要工作为复习应对考试，此时的实验课效果也不理想。根据这样的规律，实验时间安排的教学规划适宜度也不同，如表2所示。

表2 教学规划适宜度期望值

对于规划适宜度的期望函数公式为：

FEP=∑FEP(i)

(9)

根据以上分析可以得出适应度函数F：

(10)

式中：k1、k2和k3用于调控各期望值对总适应度的影响。

3.3 算法步骤

遗传算法的整体流程如图3所示。它的主要流程通过遗传算法程序产生Np组可行解，之后计算各个可行解的适应度，通过交叉、变异产生新的可行解。如此迭代，直到达到预先设定的最大代数，退出程序，输出最优结果。

根据以上的算法思路，传统遗传算法步骤如下：

(1) 参数定义：设定遗传算法中需要的种群数量、个体的染色体数量、染色体长度、交叉概率、变异概率、最大繁殖代数等参数。

(2) 产生初始种群：生成Np个随机向量，每个向量上的分量，根据一定的概率被赋值为0或1，得到一条染色体。按照个体染色体数量，将Nm个随机向量设定为一个个体，种群中共Nt个个体，并计算每个个体的适应度。

(3) 产生新的种群：通过轮盘赌选择从父代种群中选择两个个体，通过直接遗传、交叉和变异的方式产生两个子代个体。计算新生子代适应度，替换原先父代种群中适应度较低的个体。如果满足退出条件(达到最大繁殖代数)，退出计算，输出最优解；否则，重复步骤3。

在传统的遗传算法中，是设定上一代的全部个体的基因进行重组、交叉、变异得到下一代基因。但是因为实际算法运行中，两代个体之间有着一个过渡期，在这个期间，两代个体都存在，虽然避免了父代与子代间的基因传递变动太大，但是会导致寻优的“深度”不足。因此，在改进的遗传算法中，在父代与子代的种群融合前，只保留父代种群中一半适应度较好的个体，另一半较差的直接删除。这样可以提高收敛速度，增加搜索深度。

根据以上描述，本文采用的改进遗传算法步骤如下：

(1) 参数定义：同传统算法步骤1。

(2) 产生初始种群：同传统算法步骤2。

(3) 产生新的种群：通过轮盘赌选择从父代种群中选择两个个体，通过直接遗传、交叉和变异的方式产生两个子代个体。计算新生子代适应度，替换原先父代种群中适应度较低的个体。

(4) 删除处理：对父代种群按照适应度排序，保留较优的一半父代个体。重复步骤3，直到满足退出条件(达到最大繁殖代数)，退出计算，输出最优解。

4 实验验证

在Visual Studio.net环境下用C#语言编写整个调度算法的仿真实现。仿真中设定一共有5类设备，每类20台，随机生成15类实验课程，设备的服务能力如图4所示。按照10个专业20个班级每个班级30名学生，每个专业随机选择10类实验进行调度安排。

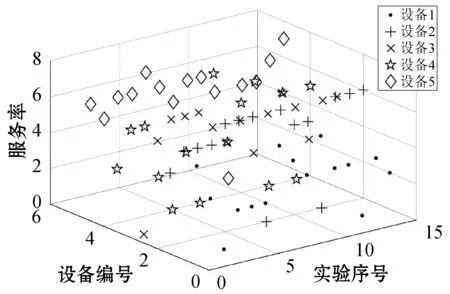
图4 设备服务能力分布图

在遗传算法中设置生育率为0.8，基因变异率为0.08。分别使用未改进算法和改进算法迭代200次，得到5次出现最优解的世代和最优解的适应度，求平均后如表3所示。

表3 遗传算法结果

遗传算法最优解曲线如图5所示，可以看出改进后遗传算法相对于原算法收敛速度明显提高，染色体经过迭代进化后可以得到最优解。按照班级分类设备使用情况可以看出，可以很好地调度设备的使用，如图6所示。从调度结果中随机调取两个班级a和b，其实验设备需求如图7所示(课程时间按照“时间段.课程段.实验类型”表示)。可以看出，在第十周第九节的时间点，两个班级同时进行实验课，分别是实验11和实验13，两者所需求的设备资源不同，其中：设备1是a班着重需要的，b班没有需求所以没有进行分配；设备5是b班所需设备，同样的a班不需要该类设备，也没有进行分配，结果符合算法的预期。图8为优化前后设备使用率对比图，可以看出，改进遗传算法的实验课程资源调度相对于传统的先来先服务设备调度的方法，设备的使用率有着明显的提升。

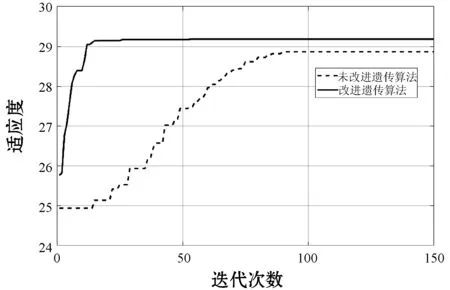
图5 遗传算法最优解曲线图

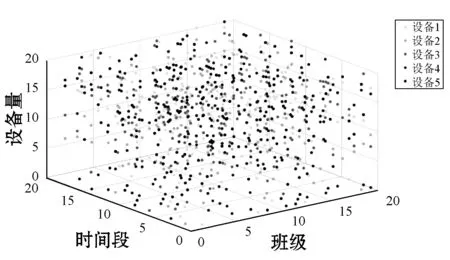
图6 各班级按时间段所需设备分布图

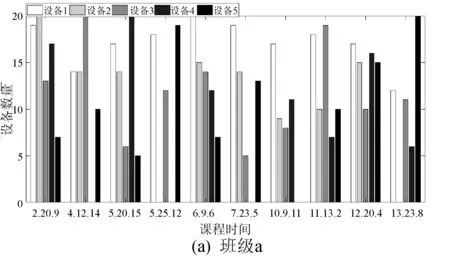
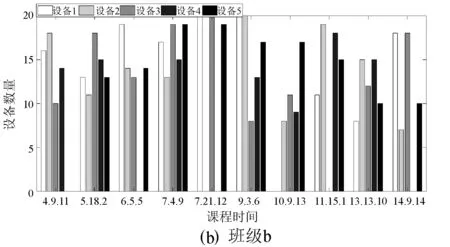
图7 实验设备需求图

图8 优化前后设备使用率对比图

5 结 语

本文论述了应对远程实验设备的调度问题，从“设备调度”、“课程安排”等多个维度建立调度优化模型，并提出基于改进遗传算法的最优化求解方法。仿真实验证明，改进型遗传算法在收敛速度和算法结果上优于传统遗传算法。优化后的设备使用率相较传统调度方式有着明显的提升，对远程实验设备资源的调度和实验课排课有着可借鉴的积极意义。