双激光场调控Be2+离子动力学的研究

白光如，齐载智，丁晶洁，李公平

(兰州大学 核科学与技术学院, 兰州 730000)

引 言

近几十年,随着激光技术的迅速发展[1-3]，使其广泛应用到了很多研究和技术领域。比如激光诱导核聚变[4-6]、飞秒激光微加工技术[7]、飞秒强激光成丝技术[8]以及强场电离机制研究[9]等。随着对于激光与物质相互作用研究的深入，相应的探测技术也得到极大地发展。目前，主要有两种测量手段对激光与物质作用过程进行观测：(1)带电粒子测量[10]。主要包括离子和光电子测量，光电子探测会受到不携带任何有用信息的背景电子干扰,而离子测量不受影响,但两种测量都需要释放光电子，只适用于电离事件的研究;(2)光测量[11]。例如光吸收谱、光成像技术等,光测量可以将量子体系的动力学信息直观地表现为光谱线型的变化，且光子间互不影响、测量不受环境影响，具有探测精度和效率高及不依赖待测体系是否电离等优点,不仅可以测量待测体系的电子电离动力学，而且还可以探测待测体系内部电子跃迁动力学和能级结构变化。

基于飞秒激光的量子相干控制因其在原子、分子研究中的重要应用而成为了近年来的研究热点[12-14]。通过改变两个激光场的相对相位，YIN等人探测到铷原子光电子的角分布并对其进行控制[15]。XU研究团队实现了强场单个高次谐波的相干控制和选择性增强[16]。基于瞬态吸收谱法，OTT等人研究了氦原子的电子动力学，发现随着红外抽运激光场强度的提高，氦原子双激发态的吸收谱型由法诺线型变为洛伦兹线型，而单激发态的吸收谱却由洛伦兹线型变为法诺线型[17]。这是由于红外强场脉冲引起了氦原子激发态偶极子相位的变化，因此提出了相位调控理论。随后，LIU等人通过理论模拟对量子相位操控产生频率梳进行研究，但是限于目前的技术水平，而无法真正在实验上实现[18]。

本文中研究高电荷态Be2+离子在强激光场中的超快动力学，利用双激光场控制Be2+离子中核外电子的运动，通过改变双激光脉冲的参量，实现对Be2+离子中二能级系统吸收光谱的有效控制。

1 计算模型

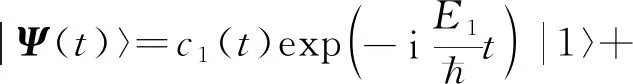
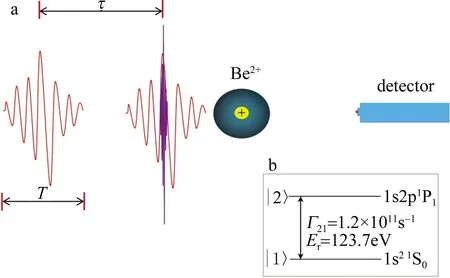
Fig.1 a—schematic diagram of phase control implementation in Be2+ system b—energy level diagram of two-level system in Be2+ system

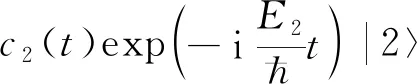
(1)

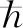
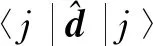
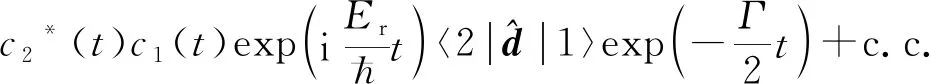
(2)

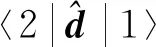
(3)

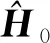
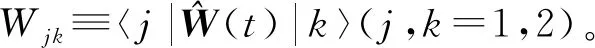
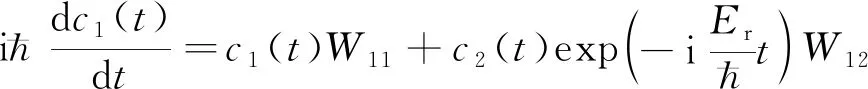
(4)

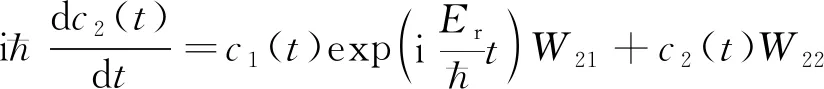
(5)

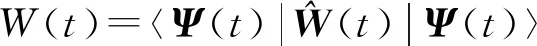
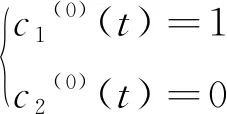
(6)

式中，上标(0)代表近似的级。为了计算1级近似，将(6)式代入(4)式及(5)式的右边得：

(7)

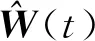
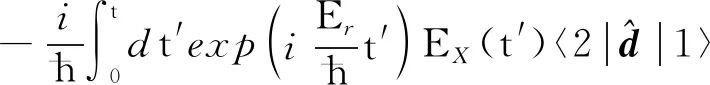
(8)

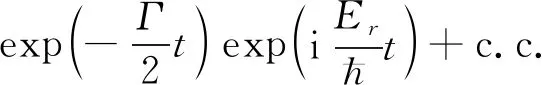
(9)

与此X射线激发脉冲同时，一束非相干的红外飞秒激光脉冲与该体系作用，飞秒脉冲由于瞬间的斯塔克效应导致激发态能级的变化。在一定延迟时间τ后，另外一束脉冲也与该离子体系作用，再次引起激发态能级的瞬间变化。激光脉冲的强度正比于脉冲的电场强度的模方，系统激发态能级的变化取决于红外激光的强度，亦取决于脉冲的电场强度：

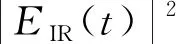
(10)

式中，IIR(t)为激光脉冲的强度。此时，偶极子表达式中的Er变为Er(t)：

Er(t)=Er+ΔEr(t)

(11)

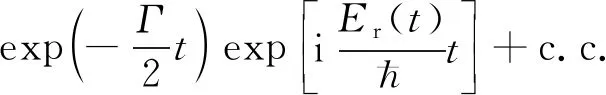
(12)

双红外激光脉冲的电场可以表示为：

ε(t)=cos(ωIRt)[EIR(t)+EIR(t-τ)]

(13)

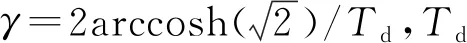
2 理论依据

He和Rb的瞬态吸收光谱研究表明，瞬态吸收光谱的谱线形状的改变对应于系统的动力学过程的演化[17,23]。实验上，可以通过观察目标系统吸收光谱线型的变化，研究其超快的动力学过程。本文中应用激光诱导相位模型，理论模拟Be2+离子体系中二能级系统的瞬态吸收光谱，研究Be2+离子在双飞秒激光电场中的动力学响应。首先，控制两束红外激光脉冲的时间延迟τ=60fs及脉冲持续时间T=5fs，改变两束红外激光脉冲的强度，研究Be2+的瞬态吸收光谱的变化，如图2所示。以下所有图中横坐标相对频率为真实能量相对于Be2+离子基态和第一激发态之间能级差的大小，即ΔE=E-Er，其中ΔE代表相对频率，E代表真实能量，Er为Be2+离子基态和第一激发态之间的能级差。一束超短的X射线激光脉冲与离子系统相作用，电子由基态(1s2 1S0)通过单光子吸收被激发到激发态(1s2p1P1)，形成一跃迁偶极子d(t)。计算中采用的衰变宽度Γ的取值不仅考虑了系统的自发辐射展宽的因素，同时也考虑了压力展宽[24]，多普勒展宽[25]与碰撞展宽[26]的影响。若没有其它电场与该体系作用，则系统的吸收谱线型为对称的洛伦兹型，如图2a中黑色实线所示。如果引入红外激光脉冲与该离子系统作用，第1束红外激光脉冲与X射线脉冲同时到达，第2束与第1束的时间延迟为60fs。控制第1束红外脉冲的强度为0.94×1012W/cm2，第2束的强度为0，结果如图2a中虚线所示。正如OTT在研究He原子的双电子动力学时的发现[17]，单电子激发的吸收光谱由洛伦兹型变为法诺型。红外飞秒脉冲与处于激发态的Be2+离子作用，其激发态由于激光电场的作用而产生斯塔克效应。由于激光电场是脉冲式的，所以斯塔克平移存在于脉冲激光的时间宽度内。处于基态的电子会随着激发态平移而发生瞬态运动，结果就表现为离子系统吸收光谱线型的变化而在低频和高频端同时出现了新的频率成分，也就是说电子的动力学过程受到了红外激光场的调控作用，这一过程可以理解为电偶极子的相位受到了红外激光电场的作用而发生改变。相位的改变量取决于红外激光脉冲的电场强度：

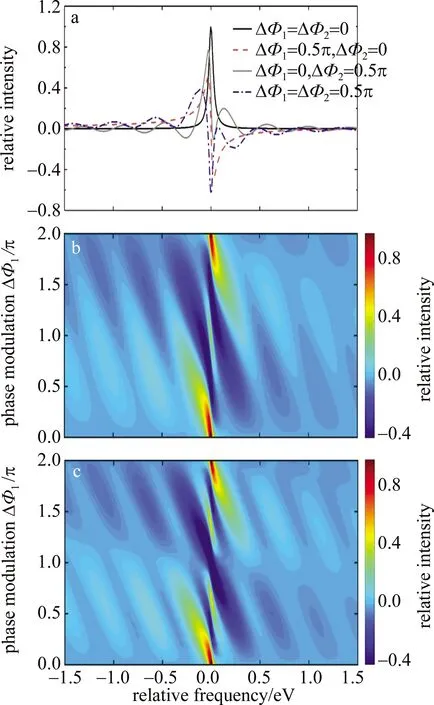
Fig.2 Be2+ ion absorption spectra with different phase changes of transition dipole

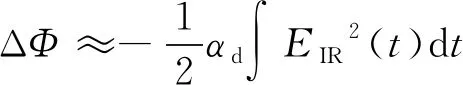
(14)

式中，αd=25.7a.u.为1s2p态的有效的动力学极化度。计算表明:实现对偶极子相位由0～π的调控，需要控制相应的红外脉冲强度从0W/cm2～1.87×1012W/cm2变化。为了表述方便，设第1束红外脉冲所引起的相位变化为ΔΦ1，第2束红外脉冲所引起的相位变化为ΔΦ2。控制第1束红外激光脉冲的强度为0，第2束脉冲激光的强度为0.94×1012W/cm2，对应的跃迁偶极子的相位变化为ΔΦ1=0,ΔΦ2=0.5π。吸收谱线变成了更为复杂的“波浪式”结构，出现了更多的频率成分，如图2a中所示。若同时控制两束红外激光脉冲的强度为0.94×1012W/cm2与Be2+作用，即ΔΦ1=ΔΦ2=0.5π，则吸收谱线型在法诺线型基础上也产生了新的频率成分，如图2中出现的“波浪式”结构所示，吸收光谱受到的调制作用更为明显。Be2+离子与相干X射线激光脉冲作用，通过单光子吸收跃迁到激发态(1s2p1P1)。由此可见，Be2+离子的吸收光谱线型受到红外激光脉冲的强度和作用时间的双重影响。可以通过非相干红外激光脉冲改变系统偶极子的相位，控制核外内壳层电子的激发动力学。

3 模拟结果分析

保持两束红外激光脉冲的强度相等，即ΔΦ1=ΔΦ2，图2b中为Be2+离子的瞬态吸收光谱对相位改变量ΔΦ1的依赖关系。相位改变量ΔΦ1从0～π变化时，可以发现每个“波浪式”结构为法诺型，由非对称转换为对称。以Er为中心，左侧的“波浪式”结构主要表现为吸收，右侧的“波浪式”结构以辐射为主。相位变化量ΔΦ1从π～2π变化时，可以发现每个“波浪式”结构逐渐由对称转换为非对称。以0eV为中心，左侧的“波浪式”结构以辐射为主，右侧的“波浪式”结构以吸收为主。“波浪式”结构随ΔΦ1的变化在洛伦兹线型和法诺线型之间转化。ΔΦ1在0～2π变化时，Be2+离子吸收光谱以π为中心呈现出中心对称形式，对应脉冲强度为1.87×1012W/cm2，吸收光谱的转化呈现出周期性，其周期为2π。控制第2束红外脉冲的强度为第1束的2倍，即2ΔΦ1=ΔΦ2，图2c为Be2+离子的瞬态吸收光谱随着相位变化量ΔΦ1的变化关系。在相位改变量ΔΦ1=π附近，在Er处可以看出其为吸收此波长的光，而图2b中，此处为发射光的形式。其原因可解释为第2束脉冲的强度很大，光谱受到更强的调制，导致此处为吸收型。但其与图2b中的整体变化趋势相同。从图2可以看出，通过控制两束激光脉冲的强度，进而改变跃迁偶极子的相位，使得光谱线型发生了显著变化，即通过控制激光脉冲的强度实现对跃迁电子的控制。

控制两束红外脉冲的强度相等并取不同的数值，使得跃迁偶极子的相位变化分别满足ΔΦ1=ΔΦ2=0.5π和ΔΦ1=ΔΦ2=π，第1束红外脉冲与X射线脉冲的时间延迟为0，红外激光脉冲的持续时间T=5fs，理论计算Be2+离子的瞬态吸收光谱对两束红外脉冲间延迟时间τ的依赖关系，如图3a和图3b所示。在延迟时间τ=0fs时，图3a呈反洛伦兹线型，图3b呈洛伦兹线型，这是由于此时第1束脉冲与第2束脉冲叠加，总的相位变化量为ΔΦ1+ΔΦ2，即图3a的总相位变化量为π，图3b的总相位变化量为2π。符合上述光谱进行周期为2π变化的规律。可以发现，对于图3a在相对频率为0eV左侧(中心频率Er左侧)，Be2+

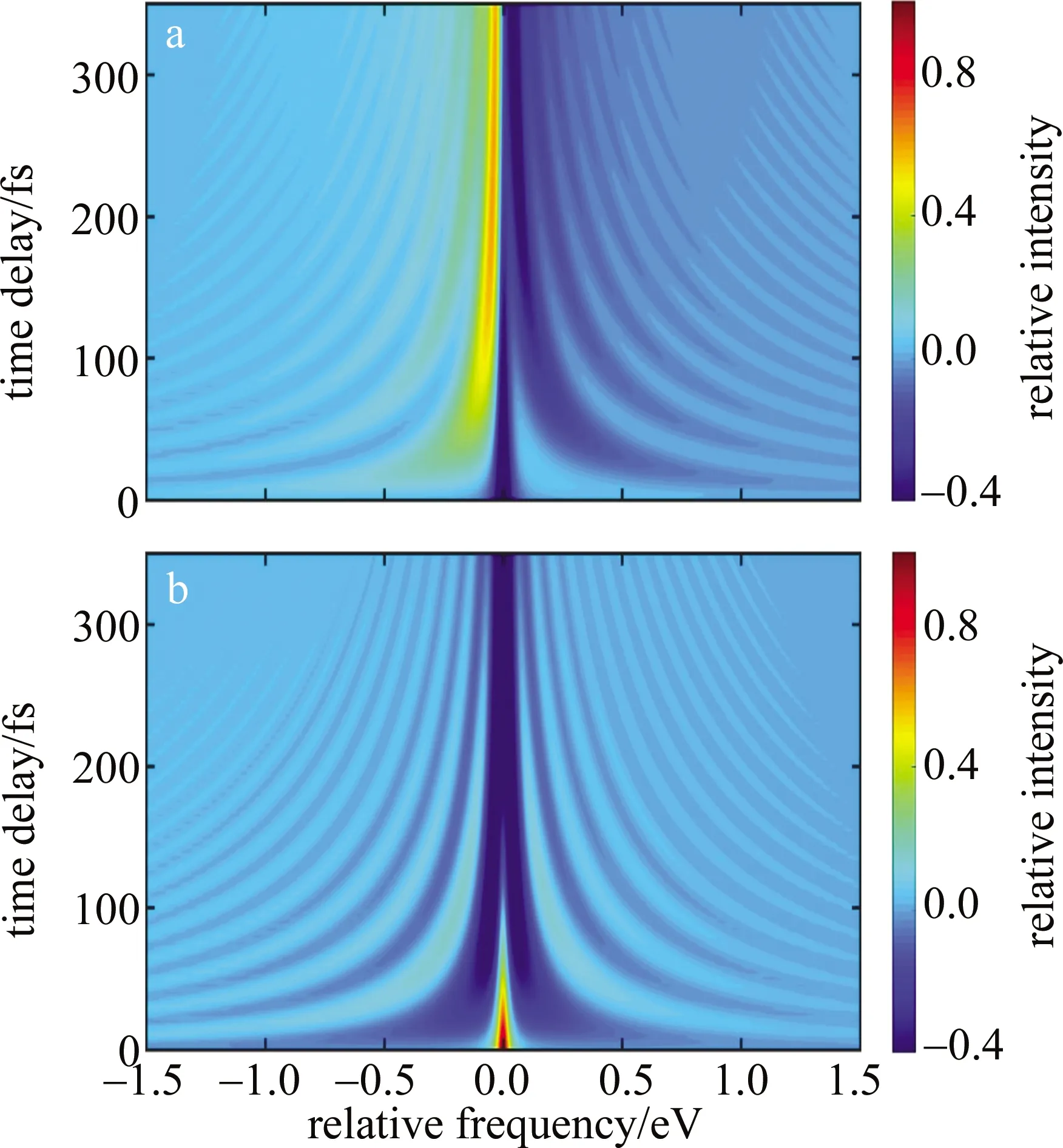
Fig.3 Be2+ ion absorption spectra with different delay timea—ΔΦ1=ΔΦ2=0.5π b—ΔΦ1=ΔΦ2=π

离子的吸收光谱表现为辐射峰，并随着延迟时间的增加振幅逐渐增加，并最终在延迟时间τ=300fs时趋于稳定。这是因为偶极子具有一定的寿命，随着偶极子的衰减，红外飞秒脉冲对光谱调制越来越弱，最终可以忽略。左侧的“波浪状”结构多为辐射成分且幅值逐渐增减并向中心汇聚。在中心频率的右侧，Be2+离子的吸收光谱首先为辐射峰，但随着延迟时间的增加逐渐转化为吸收峰，且吸收峰的幅值不断增加直到延迟时间为τ=300fs时趋于稳定。右侧的“波浪状”结构的吸收峰多为吸收成分。整个时间依赖的瞬态吸收光谱，表现为“波浪式”的结构，周期随着延迟时间τ的增加越来越小且远离中心频率的吸收峰的幅值也逐渐降低。吸收光谱的变化趋势呈现出关于中心频率0eV的类中心对称。吸收成分和辐射成分都表现为向中心频率的汇聚。

当跃迁偶极子的相位变化满足ΔΦ1=ΔΦ2=π时，图3b中为Be2+离子的瞬态吸收光谱对两束红外脉冲间延迟时间τ的依赖关系。在中心频率处，随着延迟时间τ的增加，吸收光谱首先表现为光辐射，且辐射的强度随着τ的增加而逐渐减弱，并在两侧出现吸收峰。随着延迟时间的进一步增加，两侧吸收峰的强度不断增强，并在延迟时间τ=300fs时，两个吸收峰合二为一，其强度的变化也趋于平稳，这也是由偶极子具有一定的寿命造成的，红外激光脉冲对光谱的调制越来越弱。在中心频率的左右两侧，吸收谱的谱线形状呈现出左右对称的形式，随着脉冲延迟时间τ的增加，出现“波浪式”结构，即产生新的频率成分。“波浪”周期与图3a类似逐渐减少，波谷也逐渐升高，向中心频率Er靠近。整体来看，吸收光谱呈现出以中心频率为中心的呈现左右对称形式，并随着脉冲延迟时间的增加，“波浪式”结构的周期越来越短，且强度越来越弱。对比图3a和图3b，发现其吸收光谱的“波浪式”结构的周期和强度变化趋势相同。随着的延迟时间τ增加，吸收光谱开始产生“波浪式”结构，且都在前100fs其周期减小速度剧烈，峰值强度越来越强。随后，“波浪状”结构周期仍然减小，而其峰值强度却越来越小，所有的频率成分向中心频率汇聚。这是由于跃迁偶极子呈指数衰变，随着延迟时间的增加，第2束激光脉冲对其的调制作用也逐渐降低，最后可以忽略。对于“波浪状”结构出现周期的现象，可由受微扰的衰变过程来解释[27]，即在跃迁偶极子的衰变过程中，通过红外飞秒脉冲对1s21S0～1s2p1P1相干性的调制使得“波浪状”结构出现了一定的周期。最终，图3a中的吸收光谱变为法诺型，图3b中的线型变为反洛伦兹线型，符合上述相位变化影响规律的研究。从图3可以看出，对两束红外脉冲的相对延迟时间加以控制，使得光谱线型发生了相应的变化。结果表明通过控制双激光场到达与Be2+离子的时间，即在不同时刻与受激电子作用，实现对激发态电子动力学的调控。从而达到有效控制系统光谱响应的目的。

由于红外脉冲的持续时间T对应着相位变化的上升时间，选取脉冲持续时间分别为0fs,2.7fs,7fs,35fs，研究持续时间T对Be2+离子的瞬态吸收光谱的影响。其中，0fs脉冲为delta脉冲对应相位变化的上升时间为0fs，为最理想的情况；而2.7fs为800nm红外飞秒激光脉冲的一个光周期，是其脉冲宽度可以到达的理论极限；7fs与35fs为目前实验条件下可以获得的两种脉冲宽度。对比这4种脉冲宽度对吸收光谱的影响，可以获取Be2+离子核外电子运动的准确图像。控制两束红外脉冲的强度不变，改变脉冲的持续时间，图4为对应的Be2+离子的瞬态吸收光谱。其中图4a和图4b分别对应的跃迁偶极子相位变化为ΔΦ1=ΔΦ2=0.5π和ΔΦ1=ΔΦ2=π，且两束红外激光脉冲的持续时间保持一致及延迟时间τ=60fs。随着脉冲持续时间的增加，在中心频率的左侧最高发射峰幅值逐渐增加，而在其右侧的吸收强度逐渐降低。也可以发现“波浪式”结构随着脉冲宽度的逐渐增加而峰的位置逐渐移向中心频率，远离中心频率的频率成分有消失的趋势。当脉冲宽度为35fs时，吸收光谱的“波浪式”结构在相对频率大于0.5eV时就已经消失。图4b对应相位变化为ΔΦ1=ΔΦ2=π时的结果。随着脉冲持续时间的增加，在中心频率处，光谱线型几乎不变，但是左右两侧的吸收峰的幅值逐渐减小。左侧的第1个和第2个辐射峰有显著增强。其“波浪式”结构的变化趋势与图4a大致相同。但光谱线型与图4a大不相同，这是因为红外激光脉冲对系统吸收光谱进行了更强地调制。从图4可以看出，当两束激光脉冲的持续时间改变时，光谱线型发生相应的变化。这是由于激光场持续时间的变化改变了跃迁偶极子相位变化的上升时间，引起了系统光谱响应的变化。

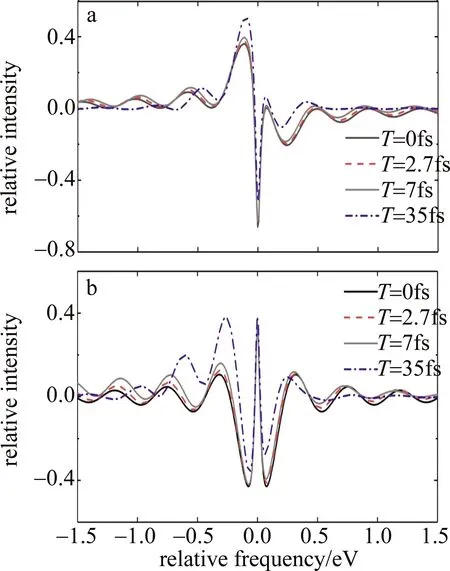
Fig.4 Transient absorption spectra of Be2+ ions at different infrared pulse durations

4 结 论

通过理论模拟，研究了Be2+离子在双强激光场中的超快动力学行为。研究发现，通过红外光场可以实现对Be2+离子的内壳层电子在激发态上运动调控，从而改变Be2+离子光谱响应，向高、低频段同时延伸，产生“波浪式”结构。这是由于红外激光电场导致了激发态的斯塔克能移，调控了受激电子的运动，表现为跃迁偶极子相位的变化。瞬态吸收光谱的谱线形状取决于红外激光脉冲的强度、相对延迟时间以及脉冲的时间宽度。