光纤中光脉冲的直线平移及幅度衰减振荡特性

伍璐琭，钟先琼，白 乐，伍 波，程 科

(成都信息工程大学 光电工程学院，成都 610225)

引 言

近些年来，由于在弯曲等离子道产生[1]、弯曲的激光成丝[2]、光学路由[3]等领域的应用，人们对具有各种弯曲空域轨道的所谓自加速光束的产生、传输和应用具有浓厚的兴趣。这些典型的光束包括艾里光束[4]、四次光束[5]、对数光束[5]等。而与空域中艾里光束对应的时域艾里脉冲在各种线性[6]和非线性光纤[7-9]中的传输也受到广泛的关注，得出了一些有趣又有价值的结果。例如，艾里光束除了具有自加速(自弯曲)特性外，还有好的自愈、近似无衍射特性，艾里脉冲传输中也具有好的自愈、抗色散和时域轨道自弯曲特性，只是由于具体的传输环境情形不同，这些特性受影响的程度不同[10-11]。研究表明，控制光束的空间谱特性，可以产生具有所需横向形状的自弯曲光束[12-14]。 例如，给高斯光束施加3阶空间谱相位可以构建艾里光束[15]。按照时空域对应和数学模型上的统一特点，则对高斯脉冲施加3阶时间谱相位可构建艾里脉冲。而参考文献[16]中发现，给孤子脉冲施加3阶时域相位调制后，也可构建类似艾里脉冲那样的弯曲时域轨道的脉冲，只是轨道弯曲的方向与3阶时间谱相位的情形有所不同。

就时域光脉冲而言，除了对高斯或孤子脉冲施加初始3阶时间谱相位或3阶时间相位以构建艾里脉冲外，以前研究较多的是施加2阶时间相位调制，在不同的色散、非线性条件下分析脉冲的时域和频域宽度及形状的变化[17-18]。发现在不同的情形下，2阶时域相位调制的存在可能导致脉冲宽度展宽、压缩或形状畸变，也可能使脉冲频谱窄化或展宽。

总之，2阶、3阶相位调制对光脉冲传输的影响都已有广泛研究，但鲜有1阶相位调制下的研究报道。在参考文献[19]中，发现施加1阶相位调制后双曲正割孤子脉冲在演化中会出现脉冲时域轨道的直线平移特性，而其它特性不发生变化。参考文献[20]中报道，高斯光脉冲在长距离演化中其时域和频域幅度都会发生衰减式振荡，脉冲脉宽也会做衰减振荡。本文中,理论研究了在给高斯脉冲施加1阶的相位调制后，脉冲在光纤中长距离传输时的形状、幅度、时间轨道的演化特性。

1 理论模型

本文中采用人们熟知的单模光纤负色散区中光脉冲的传输演化模型[20]：

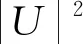
(1)

式中,U是光场复幅度，Z和τ分别是归一化传输距离和归一化的时间;UZ表示U对Z的1阶导数，Uττ则表示U对τ的2阶导数;孤子阶数N=1。1阶相位调制下的光脉冲形式如下：

U(0,τ)=exp(-τ2m/2)exp(-ibτ)

(2)

式中，b是相位调制参量，m是脉冲平顶程度的参量，m=2和m>2分别代表高斯和平顶光脉冲。U,Z,τ,m和b都是无量纲的量。

2 数值计算与讨论

以(2)式作为初始光脉冲形式，采用分步傅里叶算法数值求解方程(1)式,可得到不同相位调制参量下的高斯脉冲波形及等高线随距离的演化情况，分别如图1和图2所示。

由图1和图2可见，随着距离的增加，一方面，脉冲幅度出现了振荡行为，另一方面，脉冲的时域轨道发生了直线平移,且相位参量b的绝对值越大，则平移越厉害。当b分别为正和负时，脉冲峰值位置分别向脉冲的前沿和后沿移动，即相当于脉冲整体分别变慢或变快了。由图3a进一步可以看出，脉冲幅度Um的振荡特性与具体的1阶相位调制参量无关。而从图3b可清楚地看到,1阶相位调制参量只影响脉冲的时域位置，使其随距离的增加而发生向前沿和后沿的直线平移，图中τm表示脉冲峰值位置处的归一化时间。实际上，初始1阶线性相位调制的引入相当于在整个脉冲范围内引入了一个与脉冲位置无关的常数啁啾，+b和-b分别对应正和负的啁啾，即分别引入了一个蓝移和红移的频率元。而在负色散区，蓝色频率元相较于红色频率元传输更快些，故在+b和-b情况下，导致整个脉冲分别向前沿和后沿移动。作者进一步的研究表明，对于m>2的平顶光脉冲，引入1阶相位调制后得到了类似的结果，不同的是平顶脉冲在演化中会衍生出一些比中间主脉冲弱很多的旁瓣脉冲。这里不再图示和赘述。

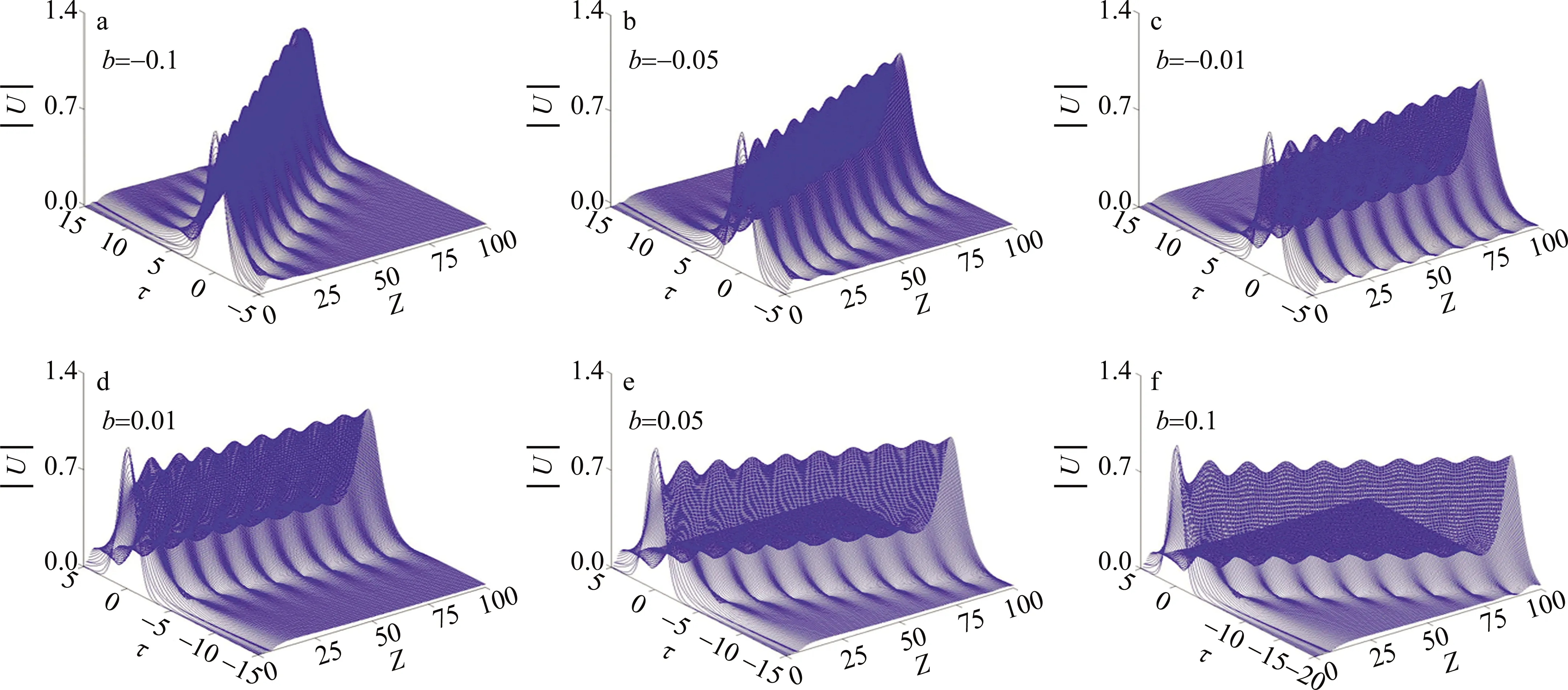
Fig.1 Shape evolution with the propagation distance of Gaussian pulses for different parameters of phase modulation

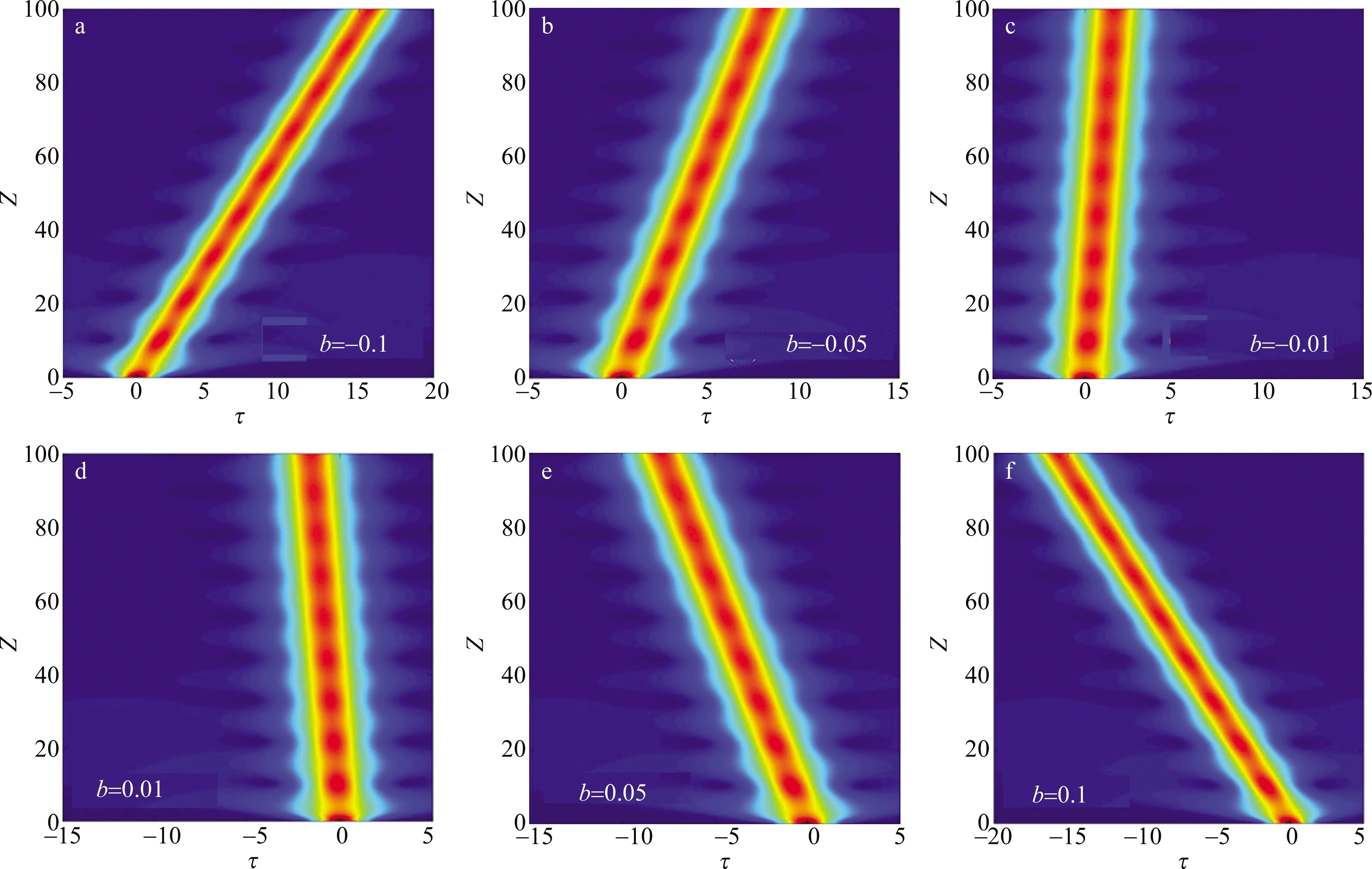
Fig.2 Contour evolution with the propagation distance of Gaussian pulses for different parameters of phase modulation

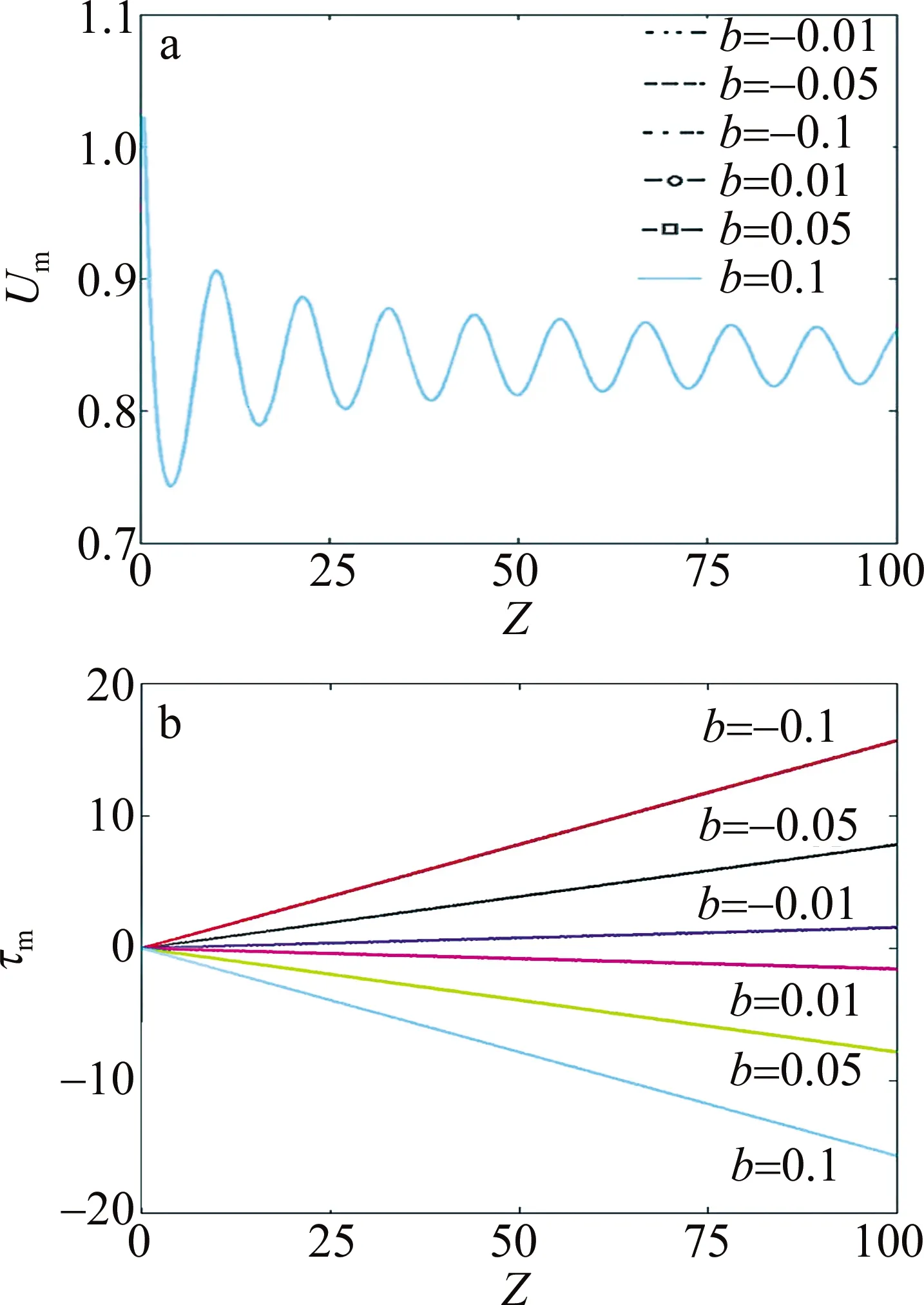
Fig.3 Peak value and position evolution with the propagation distance of Gaussian pulses for different parameters of phase modulation

3 结 论

通过对初始引入1阶相位调制后的高斯和平顶光脉冲进行数值研究后发现，在光纤负色散区的长距离传输过程中，一方面脉冲幅度出现衰减式振荡；另一方面，其时域轨道会发生向脉冲前沿或后沿的直线平移现象，平移的大小和方向由相位调制参量的绝对值和正负号决定。幅度振荡规律则与1阶相位调制参量无关。本文中的研究结果有利于促进各种非孤子脉冲的长距离演化特性的进一步研究。同时，可以通过在初始脉冲中引入1阶相位调制来使脉冲的时间轨道在传输中产生平移，并通过改变相位调制参量的大小和正负来调控其平移的大小和方向。