卡尔曼滤波在组合导航中的仿真与分析

朱 楠， 方 伟

（扬州海通电子科技有限公司， 江苏 扬州225000）

0 引 言

目前我国船舶领域多使用单一的导航方式［1］，而单一导航模式都有其不足的地方，惯性导航的误差会随着时间的累计而增大［2］，北斗导航系统使用定位服务时易暴露自身定位，且同一时间段内用户人数会受限制［3］。 本文选择以惯性导航为主，北斗系统作为辅助系统的模式。 根据卡尔曼滤波算法设计滤波器，估计位置和速度的最小误差，并利用该误差对惯性导航进行校正，从而得出运动体实时的导航信息［4］。 本文首先介绍卡尔曼滤波算法及其作为组合导航算法的优势，对组合导航建立数学模型，最后设置滤波初始值。 通过MATLAB 进行仿真实验，实验数据表明，以卡尔曼滤波作为核心算法的组合导航提供的导航参数，在精度上高于单个导航系统，且不受导航时间的限制。

1 卡尔曼滤波器在组合导航中的应用

数据滤波是去除噪声，还原真实数据的一种数据处理技术，卡尔曼滤波在方差已知的情况下能够从一系列存在噪声的数据中，估计动态系统的状态，且便于计算机编程实现。

设被估值系统的离散状态方程式为

式中，XK为系统的状态变量，UK为系统的控制变量，WK为系统的随机干扰输入，ZK为系统的测量值，VK为测量值的随机干扰变量。 状态转移阵均为已知的同时，需求验前统计量

式中，P表示状态估计协方差，Q表示系统噪声协方差，R表示测量噪声协方差。 假定{WK} 和{VK}是高斯白噪声序列，它们之间以及和X0之间均互不相关，并要求RK大于0。 （滤波过程详见参考文献［2］）

在卡尔曼滤波算法的迭代过程中，噪声协方差阵Q、R 反映了状态方程和测量方程的相信程度。 Q值增大，说明对状态递推越来越不相信；R 值增大，说明对测量越来越不相信［5］。

标准的卡尔曼滤波常用于估计线性系统在随机噪声干扰下的状态变量，但在组合导航系统中，系统的量测方程是非线性方程，需要对其求偏导以实现线性化，这种滤波方法被称之为扩展卡尔曼滤波（EKF）。 由于卡尔曼滤波算法将误差作为变量，因此可以作为组合导航的核心算法。

对惯性导航和其他导航系统提供的速度、位置信息之差进行最优估计后，校正惯性导航系统。 校正方式分为输出校正和反馈校正。 输出校正是将经过卡尔曼滤波后得到的导航参数误差最优估计，直接补偿惯性导航输出的导航参数；反馈校正是将导航参数误差最优估计，反馈到惯性导航系统的内部，对误差状态进行校正，得到导航参数的最优估计值。两种校正原理分别如图1、图2 所示。

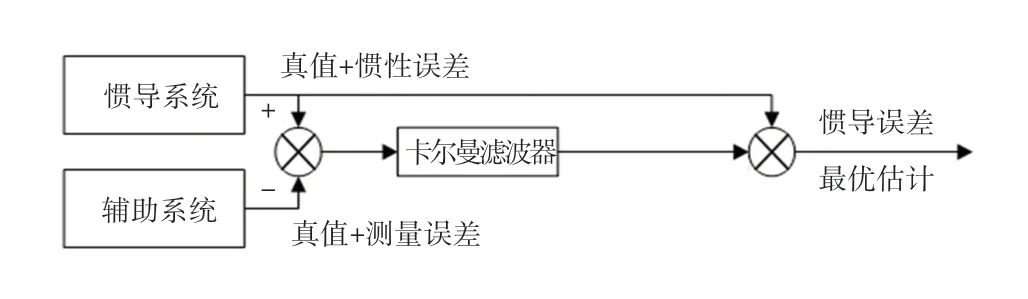
图1 输出校正Fig. 1 Output correction

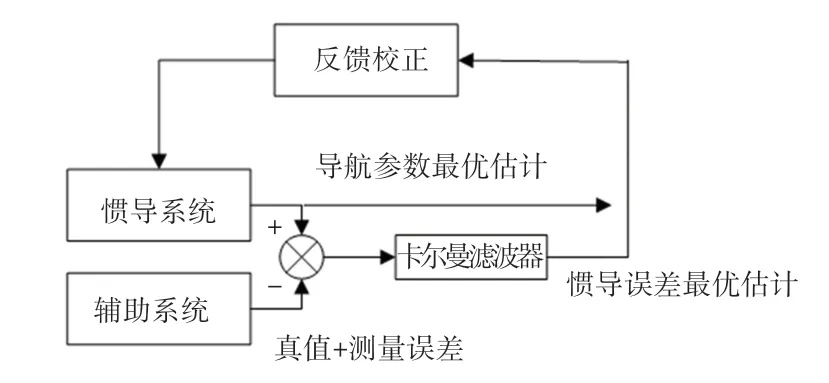
图2 反馈校正Fig. 2 Feedback correction

输出校正与反馈各自都有优缺点。 输出校正常用于惯导系统中的惯性元件精度较高，且工作时间较短的场合。 反馈校正常应用于惯性元件精度较低，且需要长时间工作的场合。

2 北斗／惯性组合导航的数学模型

选择导航算法的状态方程为惯导系统误差方程［6］，这里选择状态变量为：

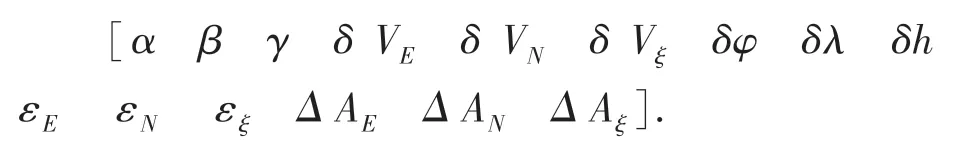
其中，从左到右依次为三个姿态角、速度误差在3 个方向上的分量、位置误差在3 个方向上的分量、陀螺漂移以及加速度计的零偏。 其中，加速度计的零偏同样可用一阶马尔科夫过程描述，即

式中各元素具体的表达式见参考文献6。

量测方程的观测量选择北斗和惯性导航分别输出的位置、速度信息之差，令量测方程为

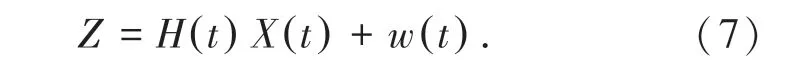
式中Z＝[Vie-VgeVin-Vgnλi-λgφi-φg]T，Vie，Vin为惯导系统输出速度信息。Vge，Vgn为北斗输出速度信息。λi，φi为惯导系统输出的经纬度。λg，φg为北斗输出的经纬度。

3 仿真结果分析

通过MATLAB 进行仿真，验证算法的可靠性。 滤波器选择输出校正方式，滤波初始值如表1所示。

表1 滤波初始值设置Tab. 4 Filter initial value setting

表中，Tg、Ta分别表示加速度计和陀螺仪的白噪声激励时间。 仿真时间为500 s，仿真结果如图3和图4 所示［7］。

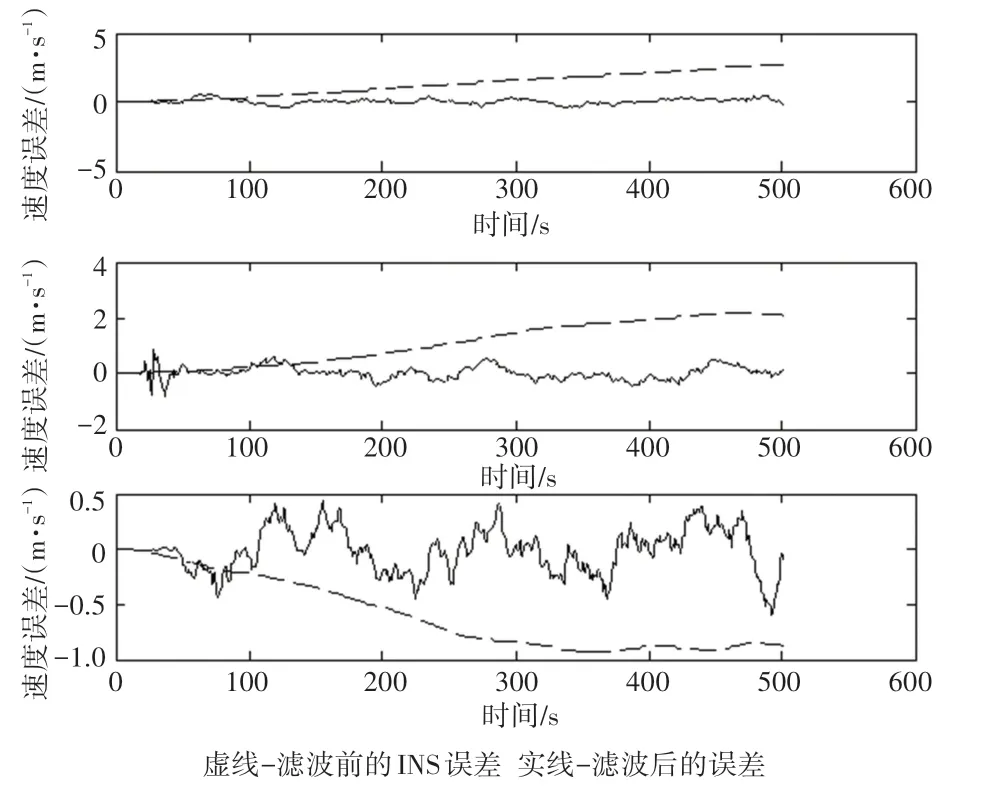
图3 滤波前后速度误差对比图Fig. 3 Velocity error contrast diagram before and after filtering

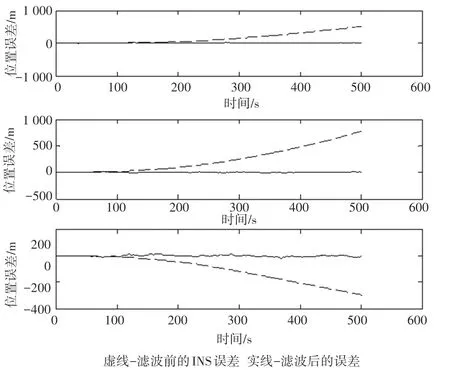
图4 滤波前后位置误差对比图Fig. 4 Position error contrast diagram before and after filtering

由图可知，北斗／惯性组合导航算法输出的位置、速度信息能够很好地跟踪运动体的真实轨迹，滤波后的误差随着时间的推移始终趋向于零。

当北斗失效时，仅由惯性导航输出的速度、位置误差会越来越大。 因此，为了进行验证，本文在仿真中人为设置3 次北斗失效的情况，得到的仿真效果如图5、图6 所示。

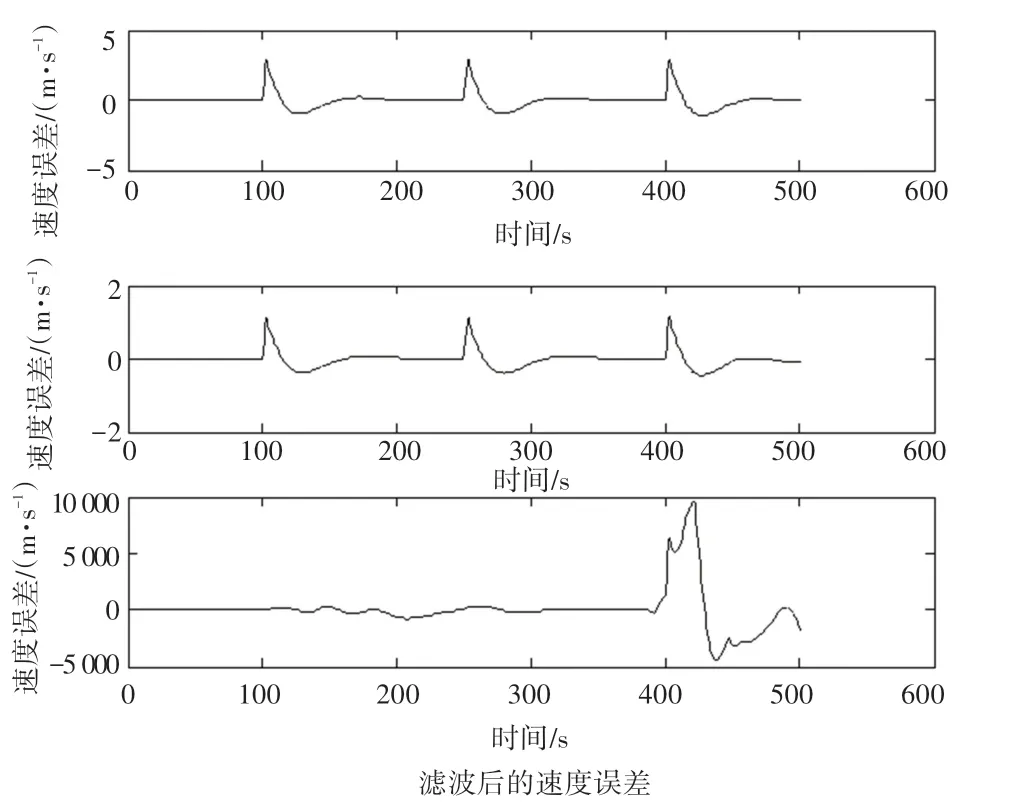
图5 北斗失效后的速度误差仿真图Fig. 5 Simulation chart of speed error after Beidou failure

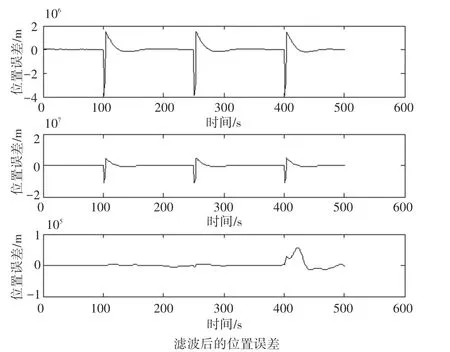
图6 北斗失效后的位置误差仿真图Fig. 6 Simulation chart of position error after Beidou failure

由图可知，当北斗失效时，无法利用北斗输出的速度、位置信息对惯性导航进行校正，速度误差和位置误差在三个方向上的分量从零刻度线处迅速上升或下降。 而当北斗正常工作时，惯性导航经过北斗校正后提供的导航信息的误差逐渐回到零刻度线处。 因此，通过误差仿真实验说明，单一的惯性导航系统无法满足运动体长时间运动状态下的定位要求，组合导航的优点得到体现。

4 结束语

本文介绍了卡尔曼滤波的基本原理以及其在北斗／惯性组合导航中的应用，通过仿真实验说明了该算法在组合导航中的可靠性，为以后的硬件实现提供理论基础与支撑。