抗野值自适应卡尔曼滤波在频率标准上的应用
陶 翠, 周威威, 唐 超, 陈春芳, 陈 铖
(上海无线电设备研究所,上海 201109)
0 引言
频率标准是一种用来提供某个特殊频点的稳定频率信号的装置或仪器。频率标准及其检测技术的进步是高科技发展水平的重要标志。频率标准的精确度直接影响导航定位装置、电力故障诊断系统、通讯网同步设备以及军用设备等的工作。所以对频率标准基准的建立、改进和测量提出了越来越高的要求。
在受到温度等环境因素干扰或出现内部故障时,频率标准输出可能会产生频率跳变[1],同时测量装置的测量误差可能会导致产生野值,最终影响频率标准的可靠性,降低系统的整体性能。野值是在实际的工程应用中,由于工作环境、测量环境的影响,或者测量仪器的测量问题导致的个别数据出现的突发性误差。所以当故障发生时,必须尽可能早地检测到故障,避免对系统产生更大影响。
频率标准跳变的检测方法主要有最小二乘算法[2]、块平均算法[3]、连续平均算法[3]、最大似然估计算法[4]、卡尔曼滤波算法[5-7]及动态阿伦方差算法[8-12]。其中卡尔曼滤波算法是一种无偏线性最小方差估计算法,属于预测性滤波算法,采用递归运算,计算成本低。卡尔曼滤波算法对频率跳变具有相对更高的检测概率,在进行滤波的同时可以基于内部的分析来更新数据,无需附加方程来检测异常数据。但是在无法确定被研究对象的精确数学模型及噪声精确统计特性时,卡尔曼滤波算法的滤波精度将大大降低,严重时甚至会发生滤波发散。同时,在容错能力上,卡尔曼滤波算法相对较差。
由于传统的卡尔曼滤波算法对野值缺乏一定的容错能力,本文中提出一种抗野值自适应卡尔曼滤波算法,并通过试验来验证算法在频率跳变检测以及抗野值方面的性能。
1 传统卡尔曼滤波
1.1 滤波模型
通常使用频率标准的平均频率偏差进行故障检测。频率标准的平均频率偏差主要由白色频率噪声(WFN)、随机游走频率噪声(RWFN)及确定性慢频率漂移[5]等组成。频率标准的平均频率偏差的递推表达式为

式中:d(0)为标准频率漂移;T为测量时间间隔;d0为线性漂移,通常为常量。
令y t(k)=yRW(k)+d(k),y t(k)代表一种频率的缓慢变化趋势,则频率标准的平均频率偏差表达式为

本文在建立平均频率偏差的卡尔曼滤波模型时,只考虑WFN 及RWFN 这两种噪声类型,对于其他噪声类型,可以用相似的特性代替,在公式中表示出来。
1.2 滤波算法
式中:ε(k)为k时刻平均频率偏差的新息;K(k)为平均频率偏差的卡尔曼滤波增益矩阵;R为v(k)的协方差矩阵;“-1”表示矩阵求逆;I为单位矩阵。其中先验平均频率偏差矩阵(k)由式(8)计算得到,频率偏差的先验协方差矩阵(k)由式(9)计算得到。
2 频率跳变检测方法
2.1 抗野值自适应卡尔曼滤波
系统存在野值时,传统卡尔曼滤波对系统状态预测的修正将会出现一定的偏差,使得滤波的结果发生偏移,甚至发散。相比于传统的卡尔曼滤波算法,抗野值自适应卡尔曼滤波算法通过新息序列加权的方式来消除野值的影响,可以有效防止滤波发散,对新息进行加权后的滤波更加接近真实状态。抗野值自适应卡尔曼滤波的状态更新方程[13-14]为
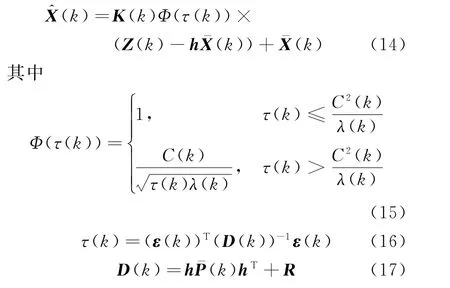
式中:Φ(τ(k))是抗野值修正因子,称为压缩影响函数,通常为光滑函数;C(k)为设定的门限值;λ(k)为K(k)D(k)(K(k))T矩阵的最大特征值;D(k)为权矩阵。当Φ(τ(k))=1 时,上述滤波为传统卡尔曼滤波;而Φ(τ(k))不为1时,则为抗野值自适应卡尔曼滤波。若系统出现野值,则τ(k)增大,根据式(15),相应的Φ(τ(k))减小,则野值在系统中的影响权重降低,野值对系统输出的影响减小。
C(k)的计算公式为

2.2 频率跳变检测方法的实施
采用抗野值自适应卡尔曼滤波算法进行频率跳变检测的流程如图1所示。

图1 抗野值自适应卡尔曼滤波算法的检测流程
选择最优累计数N,构建检测流程中的检验统计量的预测残差。
根据本文提出的抗野值自适应卡尔曼滤波算法,计算得到k时刻的N步预测后验平均频率偏差矩阵

将每个检验统计量与检测阈值进行比较,大于阈值则判定为频率标准发生故障,小于阈值则判定频率标准正常运行。
3 仿真试验验证
以铷频率标准PRS10为例,利用铷频率标准的测量数据,对抗野值自适应卡尔曼滤波算法和传统卡尔曼滤波算法检测频率跳变的性能进行仿真对比验证。
3.1 抗野值能力
通过仿真试验对抗野值自适应卡尔曼滤波的抗野值能力进行对比验证。
图2为铷频率标准PRS10的输出原始相对频率偏差数据时域曲线,此相对频率偏差数据秒稳可达5×10-12量级。

图2 铷频率标准PRS10的输出相对频率偏差数据
一般情况下,频率标准不会轻易出现故障,为了验证新算法的抗野值能力,需在频率标准输出数据中人为增加野值。对频率标准输出的相对频差数据在时刻t=1.1×104s处增加一个大小为5×10-12的值,当作野值。抗野值自适应卡尔曼滤波算法及传统卡尔曼滤波算法对相对频率偏差数据的滤波结果如图3和图4所示。可以看出,抗野值自适应卡尔曼滤波后的最大相对频率偏差约为0.48×10-12,传统卡尔曼滤波后的最大相对频率偏差约为1×10-12左右,抗野值自适应卡尔曼滤波的野值抑制能力明显强于传统卡尔曼滤波。

图3 抗野值自适应卡尔曼滤波算法对野值的抑制效果图
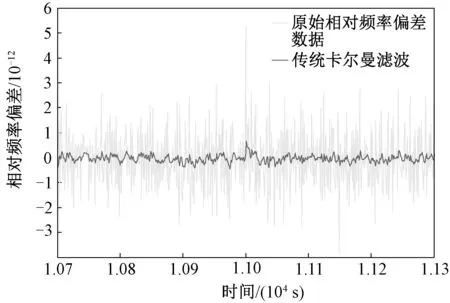
图4 传统卡尔曼滤波算法对野值的抑制效果图
3.2 检测概率和虚警率
通过检测概率及误检率仿真试验,验证抗野值自适应卡尔曼滤波算法相较于传统卡尔曼滤波算法的优势。



图5 频率跳变的累积和检测概率之间的关系
可以看出,单个曲线的累积数会随着频率跳变检测概率的升高而增大。当累积数为11时,抗野值自适应卡尔曼滤波的检测概率为0.99,传统卡尔曼滤波的检测概率仅为0.15左右;当累积数达到24 时,传统卡尔曼滤波检测概率才达到0.99。也就是说,传统卡尔曼滤波如果要达到与抗野值自适应卡尔曼滤波相同的频率跳变检测概率,就需要更大的累积数。说明抗野值自适应卡尔曼滤波性能相比传统卡尔曼滤波有了一定的提高。本文选择累积数为11来进行算法验证。
由于铷频率标准的频率漂移非常缓慢,在较短的采样时间内,阿伦方差显示的白色频率噪声分量、随机游走白色频率噪声分量和漂移分量都可以忽略不计。本文主要针对频率跳变(即铷频率标准频率偏差均值的突然变化)进行详细的讨论。仿真用数据的频率偏差在t=0.9×104s时刻发生频率跳变,相对频率偏差跳变值为2.5×10-12。传统卡尔曼滤波及抗野值自适应卡尔曼滤波得到的状态估计结果分别如图6和图7所示。

图6 传统卡尔曼滤波相对频率偏差的估计

图7 抗野值自适应卡尔曼滤波相对频率偏差的估计
可知,抗野值自适应卡尔曼滤波通过自适应调整,更新状态矩阵,使滤波精度得到一定的提高。为了验证抗野值自适应卡尔曼滤波在检测概率方面的性能优势,在固定误检率情况下对两种算法进行仿真。当误检率为10-3时,两种算法检测概率和频率跳变的关系如图8 所示。可以看出,相对频率跳变相同情况下,抗野值自适应卡尔曼滤波的检测概率高于传统卡尔曼滤波,当抗野值自适应卡尔曼滤波检测概率到达0.99时,传统卡尔曼滤波的检测概率只有0.2左右。

图8 相对频率跳变大小和检测概率的关系曲线
在相对频率跳变相同情况下,分析两种滤波方法检测概率和误检率之间的关系。使用铷频率标准的仿真数据进行模拟仿真,在累积数为11,相对频率跳变分别为1.5×10-12,2×10-12,2.5×10-12时,仿真结果如图9 所示。图中用ΔfK表示卡尔曼滤波的相对频率跳变,用ΔfA表示抗野值自适应卡尔曼滤波的相对频率跳变。两种方法的检测概率都随着误检率的增大而增大,当相对频率跳变为1.5×10-12,误检率为6×10-4时,传统卡尔曼滤波的检测概率只有0.019,抗野值自适应卡尔曼滤波的检测概率为0.370。当相对频率跳变为2×10-12,误检率为2×10-4时,传统卡尔曼滤波的检测概率只有0.020,抗野值自适应卡尔曼滤波的检测概率为0.590。当两种滤波的检测概率相同时,抗野值自适应卡尔曼滤波的误检率明显低于传统卡尔曼滤波。

图9 不同频率跳变下两种滤波算法的检测概率与误检率曲线
4 结论
本文针对频率标准的频率跳变及野值的检测提出了一种新型抗野值自适应卡尔曼滤波算法。该滤波算法充分考虑了频率标准模型的不精确性及噪声统计特性的不确定性,利用测量数据信息,进行实时在线估计并修正模型参数,以提高滤波精度,得到系统状态变量的最优估计值。当测量数据中不包含野值时,滤波算法能够充分利用有效的新息,对量测噪声进行在线估计;当测量数据中包含野值时,滤波算法能够克服其不利影响,将其控制在某个预先给定的范围内,以确保滤波估计结果尽可能地接近系统的真实状态。
仿真结果表明,抗野值自适应卡尔曼滤波对野值的抑制作用明显优于传统的卡尔曼滤波。该方法在工业应用中不仅可以及时检测频率跳变,同时能够在一定程度上减小测量误差。

