一种低复杂度的相关干涉仪测向算法

谢纪岭, 卢彦卿, 宋永刚

(南京中新赛克科技有限责任公司,江苏 南京 211153)

0 引言

相关干涉仪测向系统利用测量得到的相位差与样本库中存储的相位差进行相关比较,估计信号的入射角,样本库中的相位差数据由测向系统事先采集得到。由于采集的相位差数据已包含了阵元间的互耦、阵元位置误差和接收通道不一致性等因素,因此用测量得到的相位差与样本库中的数据进行相关比较,可以有效降低这些因素对测向的影响,从而提高测向精度。相位差测量、相关系数计算、角度估计以及相位差样本库的制作是相关干涉仪测向系统的关键。文献[1]介绍了单通道相关干涉仪相位差提取及测向实现方法,文献[2-3]旨在解决二维测向中角度搜索运算量和数据量大的问题,文献[4-8]对相关系数的计算方法进行了研究,文献[9]研究了基线镜像对称和相位模糊问题,文献[10]对比了基线组合方式对测向性能的影响,文献[11]对相位差数据库的采集方法和筛选方法进行了分析。以上都是基于实际系统采集相位差建立的样本库。以一维测向为例,建立样本库需要按照频点和角度两个维度进行数据采集并存储,频点个数与测向系统的工作带宽有关,角度范围覆盖0°～360°,因此样本库数据的采集是一项十分耗时的工作。同时,采集样本库需要在标准场地进行,采集环境与实际使用环境不一致时同样会影响测向精度。本文针对单通道相关干涉仪测向系统,对采集样本库的数据进行分析,提出使用理论计算相位差数据代替实际采集相位差建立样本库的方法,并提出了低可靠阵元的检测和相位差替代算法。

1 单通道相关干涉仪测向原理

单通道相关干涉仪仅有一个接收通道,可节省硬件资源,没有多通道系统中通道不一致带来的测向误差。但是单通道相关干涉仪需要以复杂的器件切换和更长的测量时间为代价,利用移相器获取一对阵元之间的相位差,并通过开关阵列分时切换获取多组阵元间的相位差。

1.1 阵元相位差获取

图1为单通道相关干涉仪的测向原理示意图。图中测向天线是具有9 阵元的圆形阵列天线,阵元0位于圆心,其余8个阵元均匀分布在圆周上。假设以阵元0为参考,依次对阵元1～阵元8的信号进行移相,再与阵元0的信号进行合成,合成后的信号送入接收机经过采样、放大、下变频等处理,得到阵元0与其它8个阵元的相位差φ01,φ02,…,φ08。以获取阵元1相对阵元0的相位差为例,推导单通道相关干涉仪相位差计算公式。阵元0的接收信号分别与经过4个移相器后的阵元1的接收信号相加,设阵元1 的信号分别移相0°,90°,180°,270°,与阵 元0 的信号相加,得到的和信号为

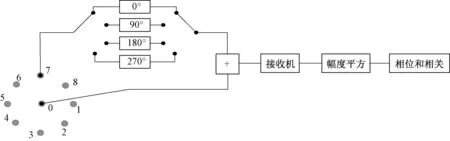
图1 单通道相关干涉仪测向原理示意图

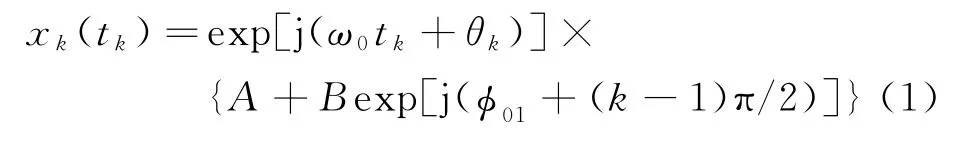
式中:k=1,2,3,4,代表4次移相;ω0表示接收信号的角频率;t k表示第k次移相合成信号的起始时刻计时;θk表示阵元0接收信号第k次移相的相位;A为阵元0接收的信号幅度;B为阵元1接收的信号幅度;ϕ01为阵元0与阵元1的相位差。

对4个和信号进行变频、滤波、放大、检波等处理,得到合成信号的幅度平方E1,E2,E3,E4,表达式为

式中:atan2(·)为求反正切函数。

按照类似的方式,可求得阵元0与阵元2～阵元8的相位差。将得到的这一组相位差以矢量形式表示为φ=(ϕ01,ϕ02,…,ϕ08)。

1.2 相关系数计算

根据测量得到的相位差矢量φ与样本库中存储的该频率下的不同入射方向的相位差矢量进行相关系数计算,最大相关系数对应的角度即为被测信号的入射角。设样本库中对应某一频率信号方向j的相位差矢量为φj,采用4种方法分别计算相关系数。

第一种是相位差直接相关法。直接计算相位差矢量的归一化互相关系数。φ与φj的归一化相关系数ρj的计算公式为

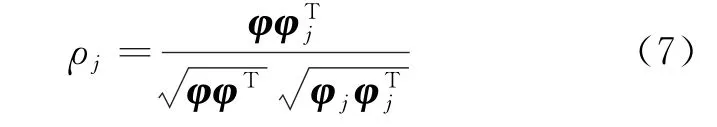
式中:T 表示矩阵转置运算。

第二种是余弦法。计算φ中每一个元素与φj中对应元素的差值,然后求差值的余弦,再求平均作为相关系数。ρj的计算公式为

实际测量得到的相位差是有模糊的,是真实相位差在主值区间[-π,+π]内的值。当真实相位在主值区间的取值接近±π时,由于受到噪声的影响,实际测量值会围绕π和-π上下波动,导致相位差直接相关法的测角误差较大。余弦法和两种改进的余弦法则不受相位模糊的影响,本文在接下来的仿真和实测中对4种方法进行对比。

1.3 传统相关干涉仪样本库数据的采集

采用相关干涉仪进行测向时,需要事先建立不同频率、不同入射方向下对应的相位差样本库。样本库是相关干涉仪测向系统的关键,只有样本库准确才能保证测向性能。样本库数据一般由实际系统在标准场地实测获得,正是由于建立样本库时将天线单元间的互耦、接收通道的非理想性等因素都考虑在内,才使得相关干涉仪测向系统具有较高的测向精度。

进行数据采集时,要求场地平坦开阔,周围无高大建筑物、树木或山体遮挡,无大功率发射源等电磁干扰存在,无高压传输线及高压铁塔。场地不小于(10～15)λ,λ为采集样本点频率的波长,发射源和接收天线之间的距离应不小于5λ。

2 相关干涉仪测向改进算法

2.1 样本库理论数据生成

本文拟采用理论相位差代替采集相位差,建立相关干涉仪测向系统样本库,根据天线阵列的布局,利用理论公式实时计算相位误差数据库,不需要事先测量和存储。以前述9阵元阵列为例,设信号入射方向与天线阵元0和阵元1之间连线的夹角为入射角α,如图2所示。

图2 阵列布局示意图

参考天线阵元0 与阵元i的相位差计算公式为

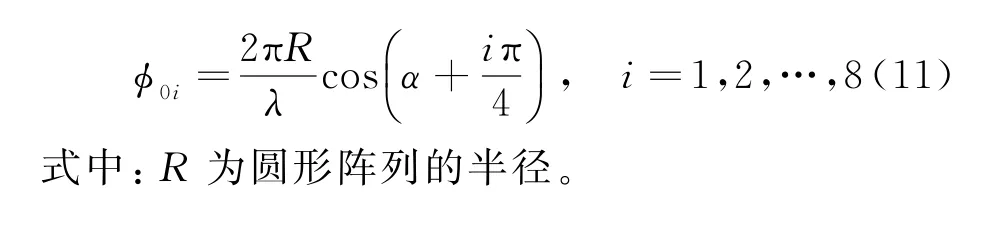
2.2 测向模糊分析

本文通过搜索相关系数最大值实现来波方向估计。当样本库中其它方向上的相位差与测量相位差的相关系数大于0.7 时,容易造成测向模糊[12]。按照此衡量标准,基于图2 所示圆形阵列,对基线波长比和测向模糊之间的关系进行仿真,如图3所示。图中的基线即圆阵直径。从图3可以看出,当基线波长比不大于2时不会出现测向模糊,而基线波长比等于2.2时会出现测向模糊。

图3 基线波长比与测向模糊关系图

2.3 阵列中低可靠阵元检测和测量值替代

上述的圆形天线阵列中,由于中心阵元和结构件的影响,当信号从某一方向入射时,正对入射方向的阵元与中心参考阵元合成信号的幅度较大,而背对入射信号方向的阵元与参考阵元合成信号的幅度较小,导致后者估计得到的相位差误差很大。例如当α=0°时,阵元1、阵元2、阵元8与阵元0合成信号的幅度较大,而阵元4、阵元5、阵元6与阵元0合成信号的幅度较小,导致基于阵元4、阵元5和阵元6的相位差估计误差较大。

为了解决该问题,首先需要检测出相位差估计误差大的阵元,然后利用其它阵元的相位差估计值推算并替换误差大的阵元对应的相位差。针对单通道相关干涉仪,每个阵元接收的信号经过4次移相后分别与参考阵元信号进行合成。4次移相值分别为0°,90°,180°,270°,设由波程差引起的信号到达该阵元与参考阵元的相位差为ϕ,则4次移相后的相位差分别为ϕ,ϕ+90°,ϕ+180°,ϕ+270°。移相后的相位差最接近0°的合成信号的幅度最大。对8个阵元4次移相后与参考阵元合成信号的最大幅度进行排序,最大幅度大的阵元对应的相位差估计误差小、可靠性高,最大幅度小的阵元估计的相位差可靠性低。利用误差小的相位差数据,根据三角公式可推算出可靠性较低的阵元对应的相位差。

3 仿真验证

3.1 相位差仿真

采用单音信号进行仿真,分析信噪比对相位差估计结果的影响。设单音信号的频率f为300 MHz,采样率为1.2 GHz,采样点数为16 384,两阵元收到的信号分别为cos(2πft)和cos(2πft+π/3),即两阵元接收信号的相位差为π/3。 在带内信噪比(0～30)d B 范围内,以1 d B为间隔,每个信噪比下仿真10 000次,相位差估计的均值和方差如图4所示。

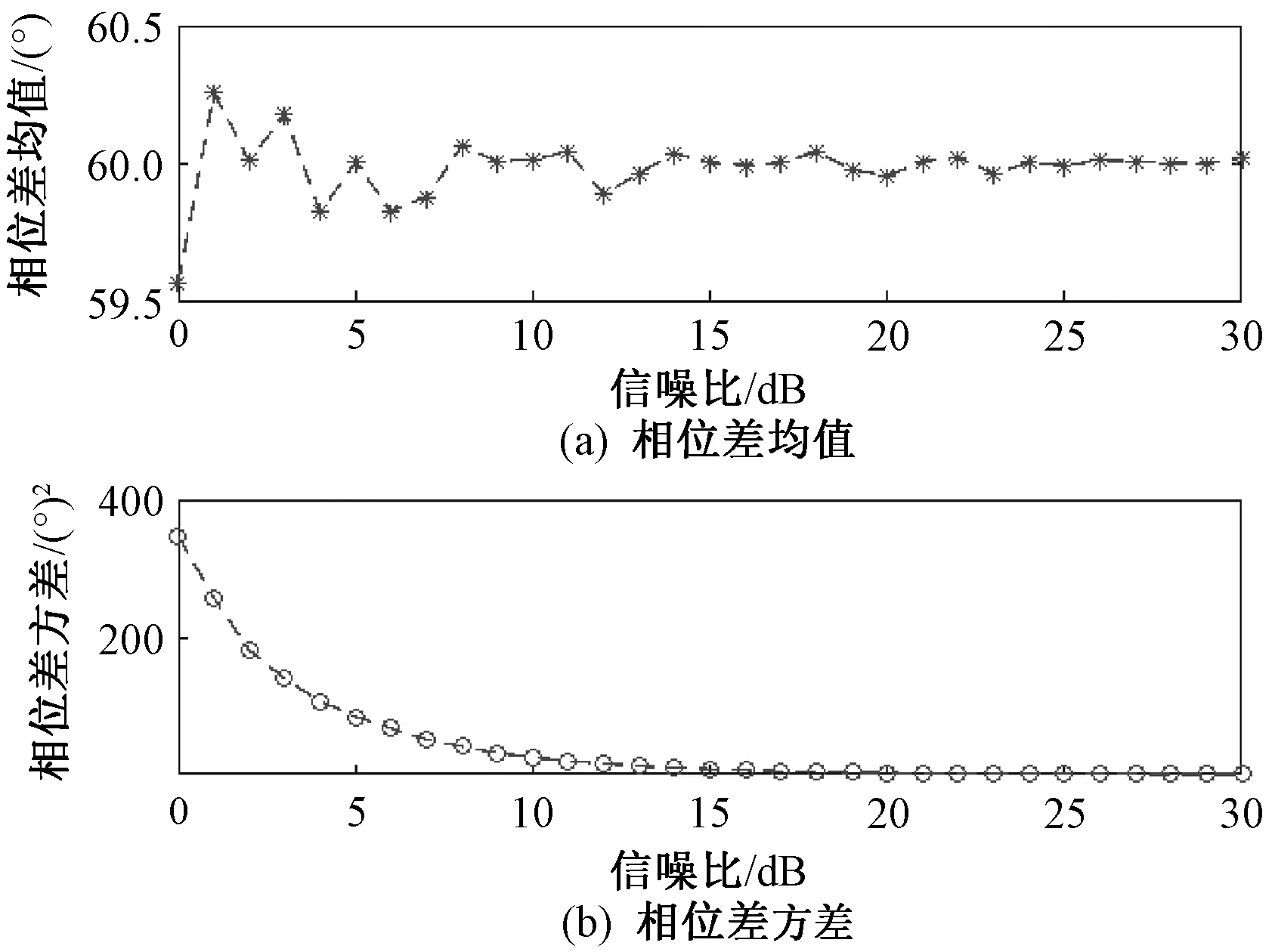
图4 不同信噪比条件下相位差估计均值和方差

3.2 角度估计仿真

测向天线采用前述的9阵元圆形阵列天线,信号频率771 MHz,阵列孔径270 mm,目标信号方位角80°。相位差测量结果的标准差为0.1°时,采用不同相关系数计算方法,相关系数的仿真结果如图5所示。可知,余弦法和改进余弦法的相关峰旁瓣较低,改进余弦法的相关峰主瓣较窄。

图5 不同相关算法的相关系数仿真曲线

采用不同的相关系数计算方法,对信号入射角度估计的均值和标准差进行仿真。设相位差测量的标准差范围为0°～0.2°,步进0.01°,在每个偏差下仿真10 000次,仿真结果如图6所示。

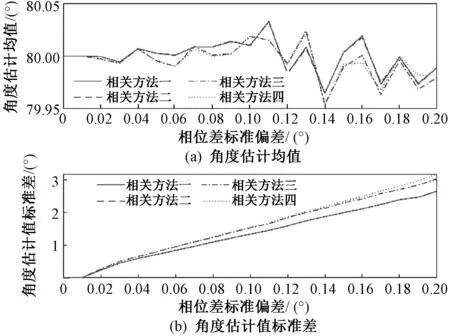
图6 入射角估计值随相位差标准偏差的变化规律

从图6可以看出:随着相位差测量偏差的增大,测向误差越来越大,误差的标准差变化更加明显;相位差直接相关法和余弦法估计结果的标准偏差比另外两种小。因此选用相关峰旁瓣较低且估计标准偏差较小的余弦法计算相关系数性能较好。

4 测试验证

在单信道相关干涉仪测向系统中对算法进行验证。(1～3)GHz 频段的天线阵列直径为0.2 m,(3～6)GHz 频段的天线阵列直径为0.09 m,基线波长比均不大于2,不会出现测向模糊。图7和图8分别是1 580 MHz频点下,对相位差测量偏差较大的阵元替换前后参考阵元与阵元5的相位差及入射角估计结果。替换前信号入射角在0°～23°和283°～360°范围内测量得到的相位差与理论值偏差很大,替换后在0°～360°范围内测量得到的参考阵元与阵元5之间的相位差与理论值基本吻合。

图7 替换前参考阵元与阵元5的相位差及入射角估计结果

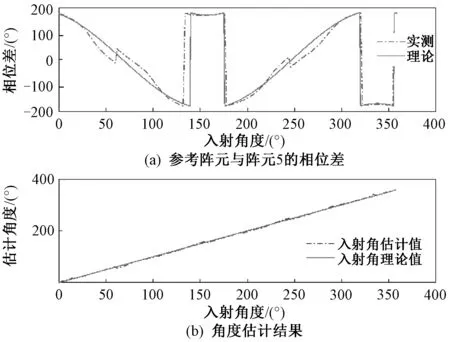
图8 替换后参考阵元与阵元5的相位差及入射角估计结果

为了验证采用理论数据库并替换信号较弱阵元的相位差数据后测向结果的准确性和适用性,在整个测向频带内选择更多频点进行测试。入射信号方位角在0°到358°范围内,以2°为间隔进行测试。入射信号频率为2 200 MHz和3 300 MHz时,参考阵元与阵元1相位差及入射角估计结果如图9和图10所示。可知,在整个测向频段范围内,测向误差不大于±3°。值得注意的是,测向误差的产生并不完全是由采用理想数据库引起的,可能与测试场地环境等有关。即使采用实际测试得到的相位差数据建立数据库,当使用场景与样本采集的场景不同时,仍然会带来测向误差。

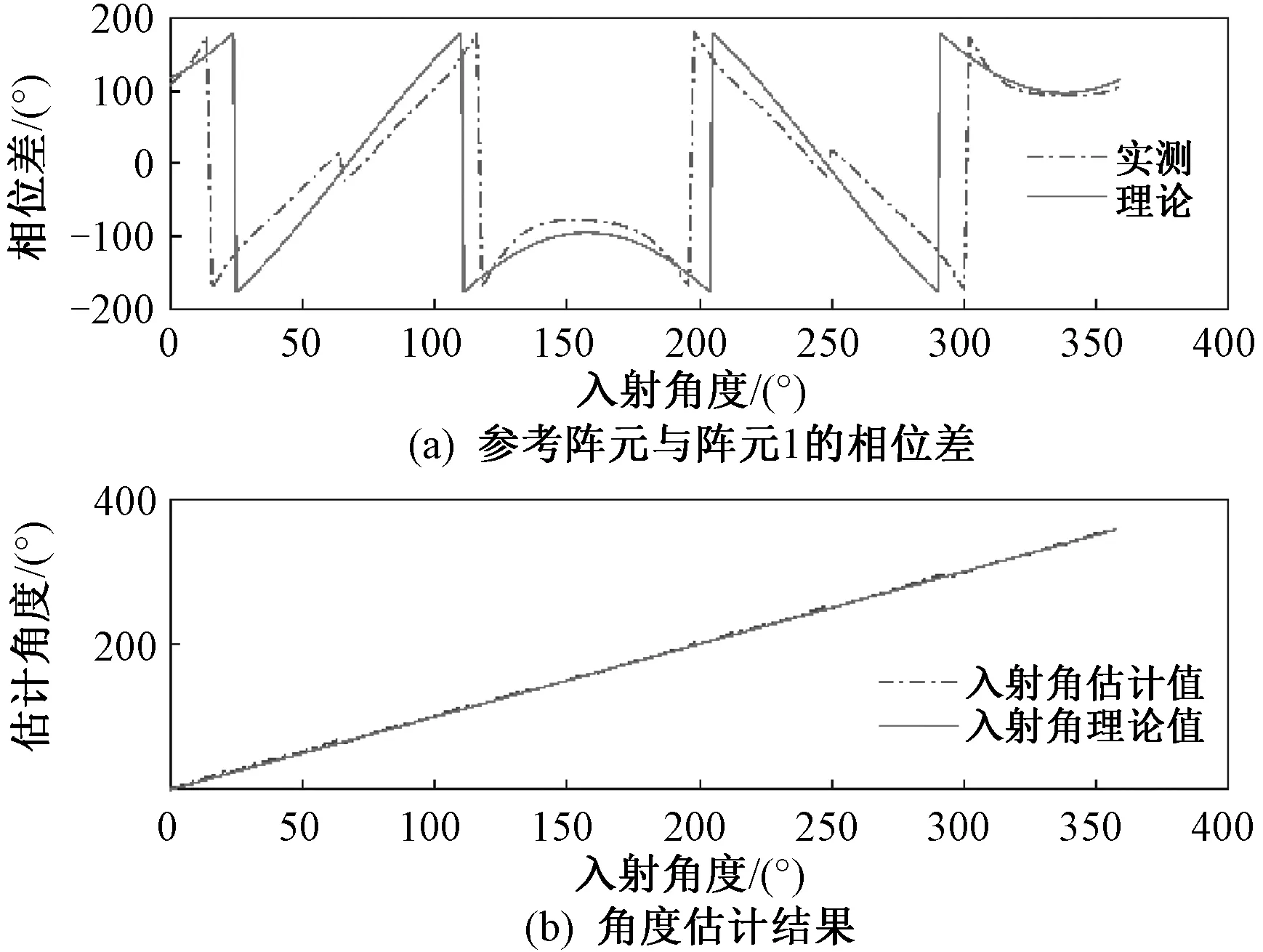
图9 2 200 MHz信号参考阵元与阵元1的相位差及角度估计结果

图10 3 300 MHz信号参考阵元与阵元1的相位差及角度估计结果

5 结束语

本文提出了一种使用理论相位差建立样本库的相关干涉仪测向算法。与传统相关干涉仪测向算法相比,该算法省去了相位差样本库采集的大量工作,大大降低了相关干涉仪测向系统工程实现的复杂度。该算法精度会受天线阵元互耦、通道幅相不一致性等因素的影响,但当上述非理想性误差较小时,该方法可以作为一种复杂度低、易于工程实现的相关干涉仪方案。针对实际测向系统中由遮挡等因素引起的阵列中个别阵元接收信号弱、相位差估计误差大的问题,提出利用接收信号较强的阵元估计的相位差推算并替代接收信号弱的阵元对应的相位差,实测结果验证了该方法的有效性。使用理论相位差建立数据库的相关干涉仪测向系统,其工程实现复杂度将远低于传统相关干涉仪测向系统。