结合边缘信息的二维Otsu 阈值分割算法研究

周向阳， 罗雪梅， 王 霄

（贵州大学 电气工程学院， 贵阳550025）

0 引 言

图像分割是图像分析、识别和理解的基础，其主要目的在于将感兴趣的目标从复杂背景中提取出来。 阈值分割法因其实现简单且有效而成为图像分割中最基本和应用最广泛的分割方法［1］。 最大类间方差法（Otsu）是阈值分割法中的经典算法［2］，利用背景和目标的类间方差最大为准则来确定阈值。但在实际应用中，由于存在噪声等干扰因素，灰度直方图不一定有明显的波峰和波谷，此时仅利用一维灰度直方图来确定阈值难以获得满意的分割效果。二维Otsu 图像分割算法［3］，准确性和抗噪声能力得到提升；快速递推法［4］的实现也使得算法的复杂度降低。 许多学者提出各种改进，如王坤等［5］根据邻域像素点与中心像素点之间的距离对邻域均值算法进行加权，并对噪声点做了一定判断，取得了较好效果；王宁等［6］通过模糊算法调整权值完成全局滤波，根据Otsu 准则并结合截距直方图求解最佳截距阈值来完成图像分割；Q. Li 等［7］通过将二维直方图中去噪重建，将像素点投影到对角线上生成灰度投影直方图；李淼等［8］采用两条通过阈值点与灰度级轴分别成一定角度的直线，对二维直方图进行区域分割，但忽略了许多有效的背景和目标点；钱卫星等［9］在斜方窄带划分的基础上，增加截距辅助轴，并依据斜分线与窄带区的交点坐标变化来划分背景和目标。 但是两条直线之间的距离固定，噪声和目标背景像素区域难以正确划分；Wang 等［10］针对邻域均值易丢失边缘和细节特征，引入导向滤波代替均值滤波，较好地保留了目标的边缘和细节；杨陶等［11］引入Roberts 算子结合线性拟合法来确定目标背景区域的双界线，运用二维Otsu 法对界线内的区域进行分割，对图像的细节特征分割较好。

综上分析研究，本文提出一种结合边缘信息的二维直方图灰度——非局部均值的算法。 引入非局部均值，改进了传统灰度——平均灰度二维直方图。利用边缘信息提出了一种新的噪声和背景目标区域划分法。 通过状态转移算法与截距阈值法来求取图像分割阈值。 实验表明，该算法应用在图像分割之中能获得更好的效果。

1 传统二维Otsu 分割方法

传统二维Otsu 法利用灰度值与其邻域均值构建二维直方图［12］。设图像尺寸为M × N，灰度等级为L，f（x， y） 为在图像（x， y） 处的灰度值，则以（x，y） 为中心的k × k 邻域内灰度均值g（x， y） 为：

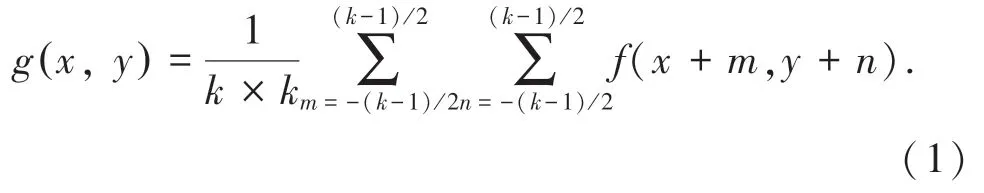
其中，0 ＜x + m ＜M，0 ＜y + n ＜N。 k 表示邻域宽度，一般取奇数。

设cij表示像素灰度值为i，其邻域均值为j 时出现的频次。 由此得到其二维联合概率密度pij为：

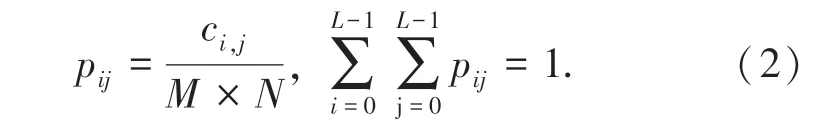
其中，0 ≤i ≤L - 1，0 ≤j ≤L - 1。

假设将图像分为背景和目标的二元组阈值为（s， t），则可将二维直方图划分为如图1 所示的A、B、C、D 四个矩形区域。

图1 灰度-邻域灰度均值二维直方图Fig. 1 Gray- the average gray two-dimensional histogram

假设区域A 和C 分别对应目标和背景，区域B和D 则表示边缘点和噪声。 因此，可求得目标和背景的概率w0，w1为：

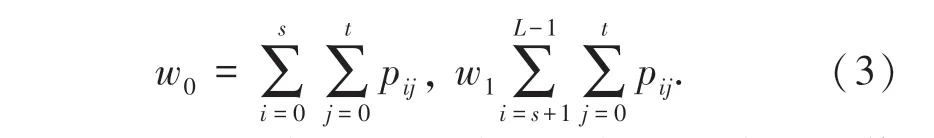
忽略B、D 区域，此时相应的目标背景类内均值矢量μ0，μ1为：

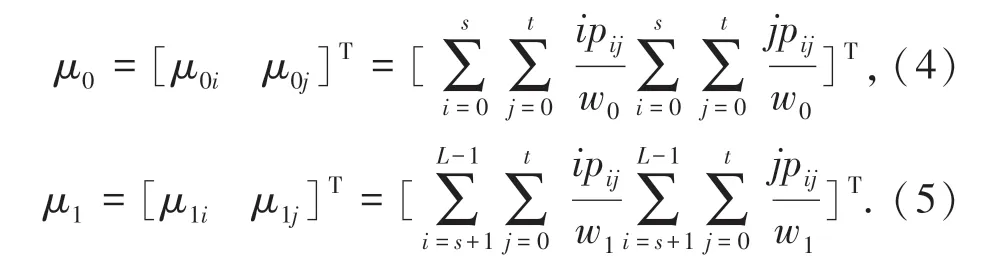
其中，μ0i、μ0j分别为目标类的灰度值和邻域灰度均值。 μ1i、μ1j分别为背景类的灰度值和邻域灰度均值。

二维直方图总体均值矢量为μt为：

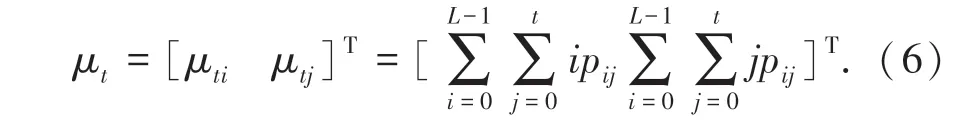
其中，μti，μtj分别为总体灰度值和邻域灰度均值。 定义目标和背景的类间离散度矩阵Sb为：

当式（8）最大值时， 所对应的（s∗， t∗） 即为分割阈值。

2 改进二维Otsu 分割方法

2.1 灰度-非局部均值直方图

传统灰度-平均灰度直方图区域划分中，通过忽略图1 中区域B 和D，来减少噪声点的干扰。 虽然在多数情况下，像素的灰度值与其邻域灰度均值基本相近，但是A、C 部分仍可能存在大量噪点，而B、D 部分也含有目标和背景的有效部分，最终导致图像分割效果较差。 此外，传统灰度-平均灰度直方图中部分目标和背景的有效点，存在因其灰度与邻域均值有一定差距而被误划分为噪声点。 因此，选择一种能更充分地衡量像素点与其邻域间关系以判断噪声点的方式也显得十分必要。

非局部均值是通过衡量图像邻域块的相似性构造加权系数，对图像进行加权平均处理［14］，具有更好的空间相关性，有利于噪声点的判断。 其核心公式如下：

其中， v（j） 为原图像矩阵，ū 为非局部均值矩阵，w（i， j）表示当前像素i 的邻域N（i）和它在Ω 搜索框内的像素j 的邻域N（j） 之间的权值系数，通常该权值系数由高斯加权的欧式距离计算得到：

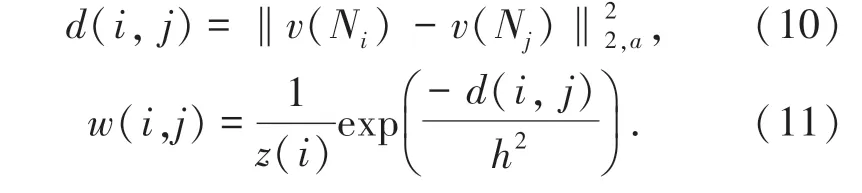
其中，a 为高斯核标准差，h 为控制权值衰减速度的参数，z（i） 为权值归一化参数，将权值w（i， j）处理到区间［0 1］ 之中。

相对于邻域平均灰度均值，非局部均值不仅利用了各像素点与其邻域像素的相关信息，而且充分考虑了各像素点搜索框内像素块之间的结构相关信息。 本文利用非局部均值代替邻域平均灰度均值构造的图像二维直方图，有利于减少噪声和目标背景区域的错分。

2.2 区域划分

绝大部分像素的灰度与其邻域平均灰度接近，边缘点的邻域灰度值会在一定程度上高于或者低于边缘点的灰度值，邻域均值与其灰度值存在一定偏差。 噪声点由外界干扰产生，其灰度值不能反映图像在该点的真实灰度值，故其灰度值与邻域均值会出现更大的偏差。 因此，可通过边缘点界线，区分目标背景区域和噪声区域［11］。 噪声和目标背景区域的界线确定过程为：

（1）边缘检测。 利用Sobel 算子获取图像的边缘点。

（2）坐标获取。 根据边缘点对应位置获取在二维直方图中的坐标（x， y）。

（3）边缘点分类。 依据主对角线分别将边缘点（x， y） 划分为上半区域S0和下半区域S1。 具体公式如下：

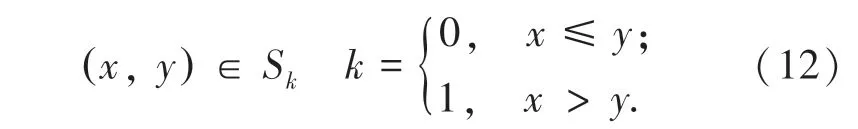
（4） 约束边缘点的获取。 分别计算二维直方图上、下区域中，与主对角线距离最大的两个边缘点（x0，y0）、（x0， y0）。 边缘点（x， y） 到主对角线距离公式为：

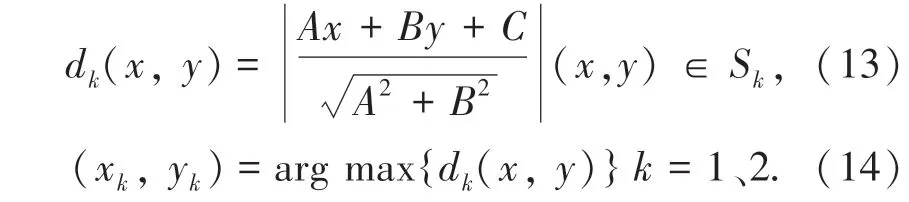
其中，A ＝1；B ＝- 1；C ＝0。 为了节省计算时间，并且使区域能更好的包含边缘点，将距离计算限制在边缘灰度值的总均值fmed± ε 的区间内，即：

其中，n 为边缘点的总个数，ε 为调节因子。 当距离一致时，选择灰度值与总均值fmed更靠近的边缘点。

（5）边界划分。 分别将（4）中得到的两个边缘点与主对角线的端点连接，得到四边形区域D，即为目标背景区域，其它区域则为噪声区域。

图2 给出了本文区域划分的效果图。 图2（a）为原始图像，图2（c）为区域划分简化模型。 图2（b）为获取图像边缘点后绘出的只含有边缘点的二维直方图，其中蓝色表示边缘点。 从分布情况可以看出，若通过曲线拟合形成界线，并不能很好地分离噪声和目标背景区域。 而本文方法所确定的界线，较好的包含了边缘点，能更好的分离噪声和目标背景区域。

图2 本文区域划分Fig. 2 Region division

2.3 截距阈值分割

若采用原始的穷举搜寻法获得阈值点（s∗， t∗），实时性较差。 本文依据二维直方图区域斜分的阈值分割思想，如图2（c），将分割线垂直主对角线，即：

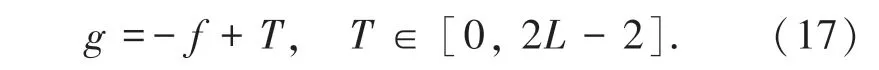
其中，T 为截距阈值。 设图2（c） D0为目标区域，D1为背景区域，则对于二维直方图中任意像素点（x， y） 有：

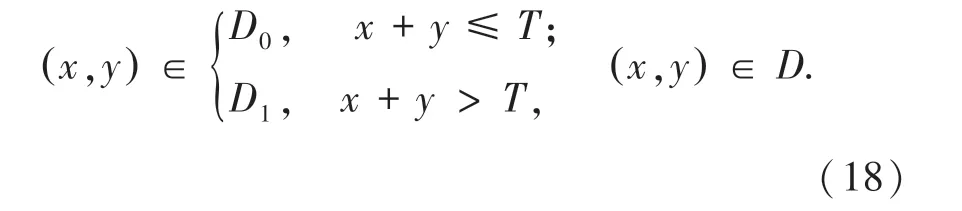
阈值T 只与灰度值和其邻域均值的和有关。 将阈值获取从二维（s∗， t∗）转换成一维T ＝s∗+ t∗阈值，减少了大量的运算时间。 结合文献［15］的一维Otsu 法可推出如下：

p（i，j）表示二元组（i， j）发生的概率，则p（T1）为：

当阈值为T 时，目标类D0和背景类D1的概率w0（T），w1（T） 分别为：

2.4 改进二维Otsu 法的实现

改进二维Otsu 算法的实现流程如下：

（1）读取图像，获取各像素点的非局部均值，建立灰度-非局部均值灰度二维直方图。

（2）通过Sobel 算子提取图像边缘点，建立边缘点的二维直方图。

（3） 通过边缘点的二维直方图确定边缘点界线，划分噪声点与目标背景点区域。

（4）对目标背景点区域采用截距阈值分割，取使得类间方差最大时的阈值。

3 状态转移算法优化阈值求解

3.1 状态转移算法

状态转移算法是由周晓君等［16］于2012 年提出的一种智能型随机性全局优化算法。 其基本思想是将优化问题的一个解当作一个状态，状态转移过程即解的产生和更新。 产生候选解的统一框架为：

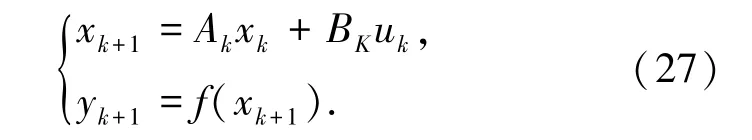
其中，xk表示当前状态，代表优化问题的一个候选解；Ak和Bk为状态转移矩阵且为随机矩阵；uk为控制变量，表示当前状态及历史状态的函数；f（·）表示目标函数。

状态转移算法的设计包括：状态转移算子的交替轮换调用策略、邻域随机采样机制、基于“贪婪准则”当前最优解的产生与更新。

状态转移算子的交替轮换调用策略有利于快速找到全局最优解和避免陷入局部最优；邻域随机采样机制可以避免穷举邻域内的所有解， 缩短算法搜索的时间；“贪婪准则”保证了算法的收敛。

3.2 阈值求解

本文利用状态转移算法的强大搜索能力，来提高图像分割的阈值求取速度。 考虑到本文求解的是最大值问题，将类间方差式（25）作为状态转移算法的目标函数，具体过程如下：

（1） 设置当前迭代次数k ＝1，随机产生一组采样大小为SE 的初始解，根据贪婪准则取采集样本中的最好解Bestk，旋转因子α ＝αmax。

（2） 以当前邻域内最好解Bestk为中心，利用伸缩变换产生SE 个样本，并更新当前采集样本最好解Bestk。 如果当前最好解Bestk有变动，则以同样机制执行一次平移变换并更新当前最好解Bestk。

（3） 采用与步骤（2） 相同机制，分别利用旋转变换、平移变换产生并更新当前最好解Bestk。

（4） 迭代次数K ＝K + 1，每执行一次迭代缩小一半旋转算子搜索半径即α ＝α／ 2。 若α ＜αmin，则置α ＝αmax，然后重返步骤（2） 直至满足终止条件。

4 实验结果与分析

4.1 实验设计

仿真实验在Matlab R2016a 环境下，Intel（R）i5 CPU ＠2.90GHz、4GB 内存、Win10 系统的电脑上进行的。 为了验证本文算法的效果， 选择图像cameraman 和菌落图像colony 进行分割研究，并将本文方法与目前经典的改进二维Otsu 方法：二维直方图叉分法、斜分法进行对比。

4.2 实验结果分析

图3 和图4 中的（b）～（d）分别展示了叉分法，斜分法和本文方法的分割结果。 可以看出，在未加入噪声的情况下，三种方法的分割结果还是有一些区别。 本文方法图3（d）中，分割后的图像杂点相比其它方法较少，图4（d）中，本文方法分割的菌落区域较完整。 斜分法和叉分法虽然在一定程度上都优化了分区问题，但是叉分法依然忽略了交叉直线外的有效点，斜分法是两条直线边界，且窄带区宽度固定，容易将一些灰度变化大的边缘点划分为噪声点。而本文方法通过非局部均值，加入像素块之间的关系，综合考虑了像素点与其邻域的关系，更准确的保留有效点和判断噪声点。

图3 Cameraman 的分割效果对比Fig. 3 Compares the segmentation effects of the Cameraman

图4 colony 的分割效果对比Fig. 4 Compares the segmentation effects of the colony

在实验图像中加入均值为0，方差为0.01 的高斯噪声，如图5 和图6 中（a）所示。 其（b）、（c）、（d）分别表示叉分法、斜分法和本文方法的分割结果。 可以看出，三种方法都有一定的抗噪性，斜分法的分割效果比叉分法要好，因为斜分法的窄带区限制了一定的噪声点。 但本文方法分割的图像噪点数量最少，分割效果最好。

图5 cameraman 加噪的分割效果对比Fig. 5 Compares the segmentation effects of the noised Cameraman

图6 Colony 加噪的分割效果对比Fig. 6 Compares the segmentation effects of the noised colony

4.3 评价指标分析

为了较客观地评价抗噪性能，本文选取了峰值信噪比（RPSN）、结构相似性度量（SSIM）、求取阈值所需时间3 个指标对算法的性能进行评价。

峰值信噪比［17］是基于对应像素点间误差的图像质量评价。 RPSN值越大，则说明分割的效果越好。 其计算公式如下：

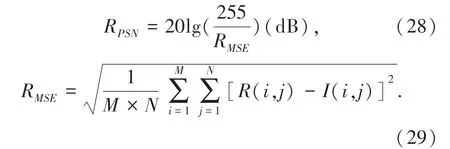
其中，R 表示原图像，I 表示分割后的图像，M ×N 为图像的大小。

三种方法分割后的RPSN值如表1 所示。 可以看出，本文方法的RPSN值均略高于其它两种算法。 因为斜分法的窄带区宽度固定，且边界为两条直线，容易错分。 而本文方法结合了图像边缘信息，能自适应的调整区域划分，更好的减少噪声干扰。

表1 三种方法的RPSN值比较Tab. 1 RPSN value comparison of the three methods

结构相似性度量［18］是一种从亮度、对比度、结构三方面度量图像相似性的图像质量评价指标，SSIM 取值范围［0， 1］，值越大，表示图像相似度越高，即分割效果越好。 SSIM 的计算公式如下：

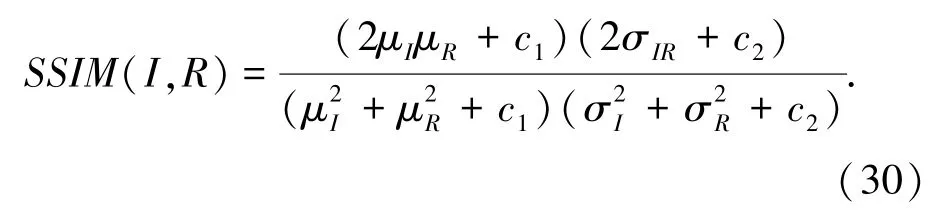
其中，μR和μI分别表示原图像和分割图像的像素平均值，σR和σI分别表示原图像和分割图像像素的方差，σIR表示分割图像和原图像像素的协方差。c1、c2为避免除零的常数。

三种方法分割后的SSIM 值如表2 所示。 可以看出，虽然三种算法都受到了一定的噪声影响，但是本文方法的SSIM 值最大，具有更好的抗噪性能。

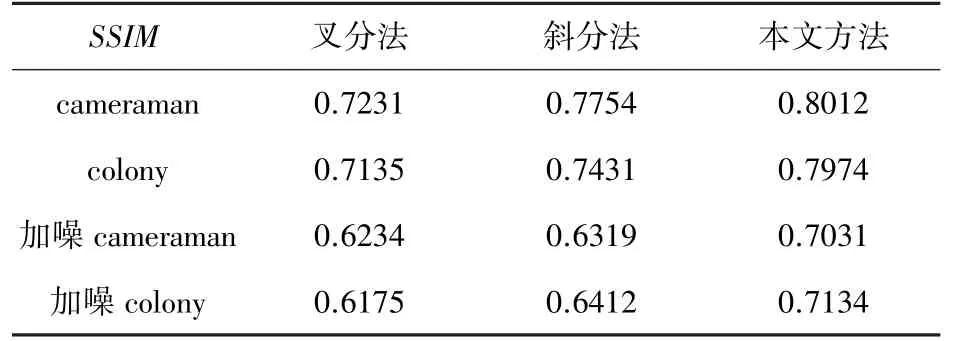
表2 三种方法的SSIM 值比较Tab. 2 SSIM comparison of the three methods

求取阈值所需的时间关系着二维Otsu 法的效率问题，是评价算法优劣的重要指标，所需时间越少，说明求取阈值的速度更快，算法的效率更高。

三种方法获取阈值所需的时间如表3 所示。 本文提出的方法，相对于叉分法、斜分法的图像的所需时间是最短的，说明本文提出的方法效率最高。 同时，也可以看出，文献［9］的斜分法的运行时间比文献［8］的叉分法要短。 因为文献［9］的斜分法通过截距阈值实现了降维处理，节省了大量时间。 而本文方法，在通过截距阈值降维运算的基础上，还利用了状态转移算法的搜索能力，取得了更高的效率。

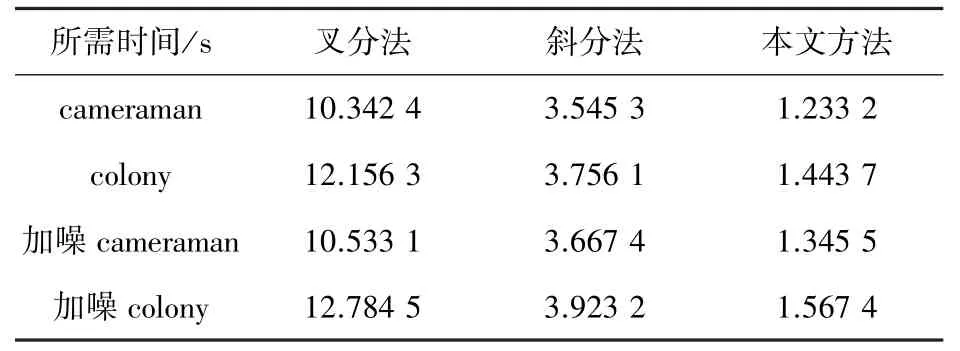
表3 三种方法获取阈值所需时间比较Tab. 3 Comparison of the time required to obtain the threshold by the three methods

5 结束语

本文分析了传统二维Otsu、叉分法和斜分法的不足，提出一种结合边缘信息的二维Otsu 优化算法。对于灰度-邻域均值二维直方图中，存在部分有效点的灰度值与其邻域均值有一定差距而被误分为噪声点的不足，本文引入非局部均值代替邻域均值，在充分考虑了像素点的空间关系，使得在二维直方图中能更准确的区分背景目标点和噪声点。 考虑到对边缘点采用曲线拟合通常得不到较好的分界线，本文通过一定约束下的边缘点与主对角线确定了噪声与目标背景类的界线。 结合边缘信息的区域划分法，能对于不同的图像自适应的、更有效的划分图像噪声、目标背景区域。 而截距阈值分割法将二维Otsu 转化为一维Otsu，降低了算法复杂度，并结合状态转移算法实现了阈值的快速求解。 实验表明，相比叉分法和斜分法，本文方法能更有效更快速的分割图像，且自适应能力强，抗噪性能好，具有一定的实用价值。