融合神经网络和泊松分解的兴趣点推荐算法

张松慧，熊汉江

1.武汉软件工程职业学院 计算机学院，武汉 430205

2.武汉大学 测绘遥感信息工程国家重点实验室，武汉 430079

1 引言

随着智能移动设备的飞速发展和多种定位技术的出现与融合，人们更容易获得有关其位置的信息。这一发展引发了基于位置的社交网络（LBSN）的出现，如Foursquare、Yelp、大众点评等。与此同时，基于位置社交网络的出现也刺激了兴趣点（Point-of-Interest，POI）等相关数据的快速积累。Foursquare在2016年宣布，它已经在全球范围内收录了超过1亿个兴趣点，其中包括关于这些兴趣点的6 亿多张照片和8 700 多万个评论等，而所有这些数据都是由5 000 多万用户分享的。基于位置的社交网络提供如下相关服务：允许用户以签到的方式与其他用户分享兴趣点相关照片、兴趣点的评论等生活经历。上述这些丰富的数据对于理解用户对兴趣点的偏好，给用户推荐个性化的兴趣点都提供了良好的机会。与大多数推荐系统一样，兴趣点推荐对用户和位置服务提供商都很重要，因为它不仅可以帮助用户探索新的或相关的位置，还可以帮助位置服务提供商针对特定的兴趣点进行精确营销继而提高企业利润[1]。传统的兴趣点推荐系统将兴趣点视为普通项目（例如书籍、电影），可以很方便地使用经典协同过滤（CF）的算法[2]来进行推荐。CF 的主要思想是通过对用户-项目交互行为进行建模来了解潜在的用户偏好和项目特征。根据数据的固有特征，推荐模型主要利用显式（用户对于项目的明确反馈，例如5星评级）或隐式反馈[3]（例如，用户购买历史、点击和浏览日志）进行推荐。大多数传统的CF 方法都是基于显式反馈，即用户给出的项目评级。不同于传统推荐系统，在兴趣点推荐系统中，研究人员们更偏好基于隐式反馈（例如，签到日志等）来预测用户对于兴趣点的偏好[4]。然而，在基于隐式反馈的推荐场景中，由于只能观察到正反馈，大多数研究工作将负反馈和未知反馈混合在一起作为负反馈（显然，将负反馈和未知反馈分开是十分必要的）[5]，因此，基于隐式反馈的个性化兴趣点推荐算法更具挑战性。

为了克服上述挑战，近年来研究人员提出了一些基于隐式反馈的兴趣点推荐算法。但是，已有的这些基于隐式反馈的兴趣点推荐算法大多存在如下的问题：

（1）由于兴趣点推荐可以看作OCCF问题[6]。因此，大多数传统兴趣点推荐算法简化了用户和兴趣点之间的隐式交互。换而言之，无论用户与兴趣点签到多少次，他们都使用二进制来表示用户是否已签到兴趣点。然而，用户的签到频率反映了用户对兴趣点的偏好程度。用户在兴趣点签到次数越多，用户可能更加偏好此兴趣点。显然，传统兴趣点推荐算法的简化策略不能帮助推荐算法准确捕捉用户对兴趣点的偏好[7]，这在某种程度上导致了有效信息的丢失。

（2）基于矩阵分解的兴趣点推荐算法把签到频率数据和传统推荐系统中的评分数据等同看待，使用高斯分布模型建模用户的签到行为。实际上，高斯分布适合建模用户的评分行为，但是不适合建模用户的签到行为。正如文献[8]所指，泊松分解模型在模拟签到频率数据方面比传统的矩阵分解模型更好，也更加符合现实中用户签到的实际行为。显然，综上所述，高斯分布的使用也会导致有效信息的丢失。

（3）大多数基于CF 的兴趣点推荐模型使用线性交互函数来模拟用户潜在特征与兴趣点潜在特征之间的交互作用[9-11]。然而，如文献[12]中所指出的，线性交互函数的表达性能过于有限，无法捕捉用户-项目之间交互的复杂结构。近年来，深度学习通过学习一种深层次非线性网络结构，能够更加精准地获取用户和项目的深层次特征表示，从而为推荐系统的研究带来了新的机遇。于是，He等人[12]提出了一个名为NCF的通用框架，它采用多层感知器的神经网络结构从交互数据中学习非线性交互函数，从而有效地捕获交互之间复杂作用。然而，NCF受到如下2个限制：（1）NCF中采用的逐点学习方法容易受到数据稀疏性问题的影响，从而限制了其推荐性能的进一步提高；（2）NCF 也将所有未观察到用户-项目间的相互作用标记为负反馈，因此，NCF的负反馈的数量较多而正反馈的数量相对较少，也会造成严重的类不平衡问题[13]。

因此，为了解决以上问题，本文在基于排序的泊松分解模型基础上融合一种混合神经网络模型，从而提出了一种个性化兴趣点推荐算法，称为HNNCRPFM。具体而言，HNNCRPFM 算法将基于排序的泊松分解模型与混合神经网络相结合提供兴趣点推荐服务。利用一种基于贝叶斯成对排序泊松分解模型建模用户对于兴趣点的签到，不再将用户-兴趣点签到频率矩阵简化为0/1矩阵，而基于泊松分布模型建模也更加符合用户实际签到行为，因此，基于贝叶斯的成对排序标准和泊松分解模型的应用避免了有效信息丢失。鉴于神经网络所提供的强大学习能力，提出利用一种混合神经网络来学习交互用户-兴趣点之间的潜在特征，从而更加高效地捕捉用户-兴趣点之间的交互作用。最后将上述2 个模型进行融合，得到一个统一的推荐模型来构建用户对兴趣点的偏好顺序，达到为每一个用户定制个性化推荐列表的目的。

本文贡献如下：

（1）为了捕捉复杂的相互作用结构，本文提出一种基于混合神经网络的方法来学习用户-兴趣点之间复杂的非线性用户-兴趣点交互关系，从而发现更多用户-兴趣点之间隐藏的相关作用，有效缓解类不平衡问题。

（2）本文采用了一种基于用户签到数据（隐式反馈数据）的统一推荐算法框架融合上述混合神经网络与基于贝叶斯排序的泊松分解模型，从而有效地改善了推荐过程中的数据稀疏性问题，同时基于泊松分布的建模相对比基于高斯分布的建模而言，更好地模拟了用户对于兴趣点的签到行为，避免了有效信息的丢失。

（3）本文基于两个数据集进行了大量实验。本文的实验结果表明，HNNCRPFM 优于主流先进的兴趣点推荐算法。

2 相关工作

本文的工作涉及三个方面的相关研究工作，即兴趣点推荐、神经网络和排序学习。下面本文分三个部分回顾这三个研究领域的最新进展。

2.1 兴趣点推荐

传统的协同过滤（CF）技术已被广泛研究用于POI推荐。Ye 等人基于朋友对于用户偏好的影响，提出了基于朋友的协同过滤（FCF）方法用于POI推荐[14]。然后证明时间上下文信息和地理信息对兴趣点推荐的推荐结果有着很深的影响[15-16]。在文献[17]中，通过考虑POI转换和距离约束的一阶马尔可夫链，提出了基于张量的FPMC-LR 模型。Feng 等人[18]将时序信息、个人偏好和地理影响整合到个性化排名度量嵌入模型中，以提高推荐性能。这些工作都是基于传统的CF模型捕捉用户和POI之间的交互来构建推荐模型。任星怡等人[19]提出了一种用于POI 推荐的上下文感知概率矩阵分解方法。该方法有效整合了文本信息、地理信息、社会信息，分类信息和流行度信息等因素从而提供兴趣点服务。卢露等人[20]则提出一种基于主题模型的兴趣点推荐算法，在推荐过程中同时考虑了用户的偏好分布和兴趣点的主题分布，确保当用户面对新的兴趣点时，也能获得较好的推荐结果。李心茹等人[21]针对兴趣点推荐过程中存在的冷启动问题和数据稀疏性问题，提出利用潜在的狄利克雷分配主题模型挖掘用户的兴趣话题，融合签到数据进行相似度度量，解决冷启动问题。在推荐生成阶段提出了一种动态预测法，动态填补缺失的访问概率，进一步缓解数据稀疏性问题。但是在文献[22]中，Zhao等人提出了一种基于排名的成对张量分解框架，名为STELLAR。STELLAR 结合了细粒度的时间背景（即月、工作日/周末和小时）并带来了显著的改进。所提出的贝叶斯概率张量因子分解框架，从用户的隐性反馈中建模用户对于兴趣点的偏好。显然，具有隐式反馈的推荐系统比具有明确显式反馈的兴趣点推荐系统更实用。因此，最近关于兴趣点推荐的研究方向已经转向基于隐式反馈中学习用户的偏好，而不是从显式反馈推断用户的品味。

2.2 神经网络

神经网络技术在图像处理、自然语言理解、语音识别领域取得了巨大成功。许多研究工作都在融合神经网络与基于CF 的推荐任务，从而更好提高推荐系统的性能。有些研究工作侧重于利用自动编码器[23-24]或CNN等深度学习模型来模拟辅助信息（文本或图像），以建模潜在用户或项目特征。典型的方法包括协同深度学习（CDL）[24]和卷积矩阵分解（ConvMF）[25]。前者使用SDAE 来建模文本，而后者则认为像SDAE 这样的词袋模型存在固有的缺点，转而提出使用CNN来学习相关潜在特征。另外有些研究工作则基于神经网络直接进行推荐。例如，Gong等人[26]提出了一种基于注意力机制的CNN 推荐系统，用于微博中的哈希标签推荐。它将哈希标签推荐视为多类别分类问题。文献[27]则提出了一种建立在RNN上的非参数推荐模型。它能够模拟项目的时间性演变和用户偏好随时间的变化。它使用两个LSTM网络作为构建块来模拟动态用户状态的变化。

2.3 排序学习

个性化推荐系统的大部分研究关注已转向利用隐式用户反馈进行推荐。 由于隐式数据集提供极其稀疏的单类反馈，因此基于隐式反馈推断用户偏好极具挑战。而本质上来说，基于CF 的方法都是基于逐点回归的理论来预测用户的偏好。为了解决这个挑战，现有研究工作大多采用基于成对的方法。

在推荐模型中，最具代表性的基于成对方法的模型是BPR 模型[28]。BPR 的目标函数是最小化隐式用户反馈引起的项目成对排名损失。本文将BPR模型的扩展分为以下两个方面进行综述：（1）多重隐含反馈的BPR。Pan等人[29]通过调整成对偏好的置信水平来扩展BPR 以适应不同的隐式反馈。后来，Qiu 等人[30]研究了辅助反馈与目标反馈之间的相关性，并通过考虑不同隐式反馈的特征提出了一个综合模型。虽然这对于提高原始BPR模型的性能是有效的，但它们不一定需要异构所有的隐式反馈。（2）将BPR模型与神经网络集成。作为一种混合方法，He等人[31]提出了一种视觉BPR模型，其中CNN 用于提取视觉特征。Ding 等人[32]通过使用CNN 从社交网络中提取用户特征，从而将BPR 与神经网络结合起来。

本文提出的HNNCRPFM 算法在如下几个方面与前人的研究工作[7，33]有很大不同。首先，文献[7]的工作只是仅仅将BPR模型和泊松分解模型简单的结合，通过这种方式，文献[7]的工作有效缓解了数据稀疏性问题。但是，由于BPR模型仍然依赖于简单的矩阵分解，所以它无法正确捕捉复杂的潜在用户-兴趣点交互。另外，BPR 模型将所有未知反馈视为负面反馈，因此文献[7]仍然无法缓解类不平衡问题。相对比，HNNCRPFM 是一个基于混合神经网络成对排序的兴趣点推荐算法，混合神经网络具有深层次的非线性网络结构，具有强大的学习数据本质特征的能力，能够获取用户和兴趣点的深层次特征表示。其次，与普遍采用基于多层感知器捕捉非线性交互特征方法[33]不同，本文采用一种混合神经网络来捕捉深度非线性特征，有效地缓解了类不平衡问题。本文的实验结果表明，HNNCRPFM 算法相比现有主流先进兴趣点推荐方法而言，展示了更加卓越的性能。

3 预备知识与问题

3.1 问题

POI 推荐问题是在给定用户-POI 签到记录的情况下给用户推荐POI。让U={u1,u2,…,uM}表示一组用户，其中每个用户拥有一个位置lj。让L={l1,l2,…,lM}表示一组POI，其中每个POI拥有一个地理标识，这个地理标识由<经度，纬度>表示。用户签到频率反映了用户对兴趣点的偏好程度。现实中，用户签到频率数据是十分稀疏。

3.2 泊松分解

正如文献[34]所指出，泊松分布是更合适作为基于隐式反馈的兴趣点推荐建模。如图1所示，泊松分解模型作为概率模型，假设用户签到兴趣点分布服从泊松分布，即期望fij:rij～Poisson(fij)，期望矩阵F被分解为用户潜在因子矩阵UK×M和兴趣点潜在因子矩阵LK×N。元素uik∈U和元素ljk∈L假设服从 Gamma 先验分布。然后本文得到如下生成过程。

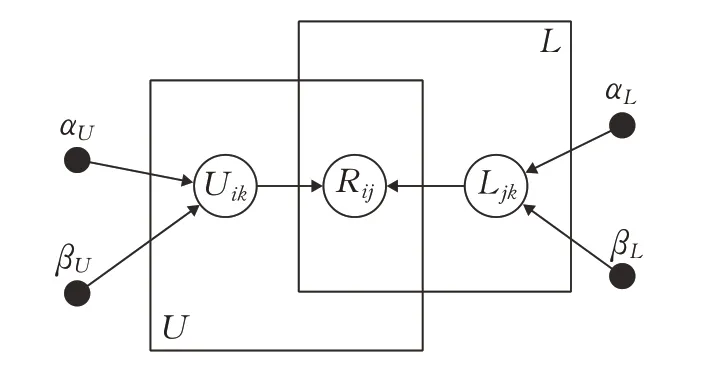
图1 泊松分解概率图模型

（1）生成用户潜在因子：uik～Gamma(αU,βU)。

（2）生成兴趣点潜在因子：ljk～Gamma(αL,βL)。

（3）得到rij～Poisson(uikTljk)。

因此，基于期望矩阵F和Gamma 先验分布应用最大后验（MAP）估计得到如下公式：

其中：

其中，参数αU，αL和βU，βL为Gamma 分布的形状参数和尺度参数，Γ(· )为伽玛函数。

基于用户和兴趣点潜在因子的后验分布，得到如下目标函数：

基于随机梯度下降算法学习用户潜在因子矩阵U和兴趣点潜在因子矩阵L，得到如下公式：

4 HNNCRPFM模型

如文献[12]中所指出的，线性函数的表达性是有限的，可能不足以捕获用户交互的复杂结构，这阻碍了基于排序的泊松分解模型的性能。为了使得泊松分解模型具有更好的捕捉复杂用户-兴趣点交互结构。本文的动机是通过基于排序的泊松分解模型建模隐式频率反馈来学习用户偏好和兴趣点特征，同时通过一种混合神经网络对用户-兴趣点交互的复杂结构进行精准建模。因此，本文在提出一种基于排序泊松兴趣点模型之上融合混合神经网络的个性化排排序模型，称为HNNCRPFM。

该模型赋予了基于排序的泊松因子模型具有高水平的非线性捕捉能力。在接下来的部分中，详细阐述本文提出的模型。

4.1 基于混合神经网络的协同排序模型

在本节中，首先提出了一个基于混合神经网络的协同排序模型，如图2所示。如文献[12]中所指出的，线性函数的表达性是有限的，可能不足以捕获用户交互的复杂结构，这阻碍了基于排序的泊松因子模型的性能。因此本文采用非线性函数——一种新的混合网络进行建模。而本文设计的这种新的混合神经网络受到广度和深度学习（Wide & Deep Learning）方法思想的启发。该方法首次提出是为了给谷歌应用商店提供App 推荐[35]。广度学习组件是一个单层感知器，是一个线性模型，具有从历史数据中捕捉直接特征的能力；而深度学习组件是MLP，能够生成一般的表示来捕获泛化。Guo等人[36]提出了深度分解机（DeepFM）作为广度和深度学习（Wide & Deep Learning）方法思想的典型应用。DeepFM 是一个端到端的模型，结合了因式分解机和MLP。它能够通过深度神经网络对高阶特征交互进行建模，通过因式分解机对低阶特征交互进行建模。因此，设计思路：首先采用基于神经网络模型，即一种浅层模型，从而应用线性映射来模拟潜在用户和项目向量的相互作用。同时采用标准MLP来捕获用户-项目潜在结构。MLP的多层特性使其能够学习各种级别的用户项目潜在结构，尤其是潜在特征之间的非线性相互作用。而如同本文文献[12]指出，简单的连接潜在特征无法准确捕捉用户-项目潜在结构，于是，在连接的向量上添加了隐藏层。通过将上述两个模型融合在一起，让上述两个模型共享相同的嵌入层，得到了最终本文提出的混合神经网络。这个混合神经网络同时具有线性和非线性优势，使得最终的推荐系统提高了推荐的准确性和多样性。如图2 本文的混合神经网络的协同排序模型采用如下结构。左边模块部分使用神经网络，基于用户与兴趣点潜在向量之间的元素乘积来捕获相关特征，右边模块部分则利用标准MLP的多层特性来学习用户和兴趣点之间的潜在特征。然后，将左右两个模块部分进行连接，即让它们独立地使用不同的嵌入层，再结合各自学习到的交互函数的输出融合在一起。这样使得应用线性映射来模拟潜在用户和兴趣点向量的相互作用，同时应用非线性函数来模拟特征的潜在结构。将它们融合在一起可以增加模型的容量，同时防止过度拟合。

图2 基于混合神经网络的协同排序模型体系结构嵌入层

基于混合神经网络的协同排序模型的网络结构可以分为嵌入层、隐藏层和输出层三层来描述。

嵌入层是为了把用户和兴趣点都转化到共享的低维潜在特征空间中，获得每个用户和每个兴趣点的稠密向量表示。形式上就是把从输入层中得到的（用户、观察到的签到兴趣点、未观察到的兴趣点）三元组(u,li,lj)，然后转换为三个嵌入向量Uu、Li、Lj。

隐藏层，本文分两个部分阐述基于混合神经网络的协同排序模型的隐藏层，先介绍左边部分，然后介绍右边部分。

（1）右边部分模块

如图2，右边部分的隐藏层是构建在嵌入层之上的一组完全连接的网络层（如图2，右边红色和蓝色部分所示）。嵌入层中得到的稠密向量串接在一起之后，能够得到一个代表用户偏好和兴趣点属性的连接向量，再将这个连接向量输入隐藏层。隐藏层是使模型具有高度非线性相互作用能力的关键，尤其是最后一层隐藏层的大小，能够决定模型的能力，称之为预测因子。

假设N表示右边部分隐藏层的层数，连接向量在隐藏层中一层一层的向前传播，故可将交互函数z写成：

在左边部分的隐藏层中的具体传播表示如下：

其中，zc(c=1,2,…,N)表示第c层的映射函数，w和τ分别表示权重矩阵和偏置向量，δ代表激活函数。本文选择使用了ReLu函数作为隐藏层的激活函数。在网络架构方面，本文采用的是与文献[12]相同的塔式模式。基于这种结构，更高隐藏层能够为用户和兴趣点学习更多的抽象特征。

（2）左边部分模块

左边部分其实是无隐藏层的，建立在嵌入层上面的一层是一个点乘的连接层。假设这一层的潜在向量是z1，那么将该向量投影到输出层，得到输出值xuij，得到如下公式：

其中，⊙是指两个向量之间相应元素之间做乘积。

预测层是整个基于混合神经网络的协同排序模型神经网络层次的最后一层，它能够结合左边和右边2个部分的模块各自学习到的交互函数的输出，将它们融合在一起。预测层的输出结果就是整个神经网络的输出，输出的预测值为ruij，表示通过这个模型训练得出的用户u对兴趣点li的偏好胜过对兴趣点lj的程度。故整合公式（9）和公式（11），预测层的输出值表示如下：

其中，xN-1代表右边模块的第N-1 层输出层。这一层的激活函数使用sigmoid 函数，因为这样就可以保证输出值的范围在 [0,1] 之间。这两种左右两个模块的学习过程是不同的，它们的最优嵌入维数和权值存在很大的差异。本文通过连接它们的最后一层隐藏层来融合这两个模型，才使得左边模块和右边模块的实现独立嵌入，因此，得到最终的输出如下公式：

4.2 基于贝叶斯排序的泊松兴趣点推荐模型

在实际的推荐系统中，用户和兴趣点之间的隐式交互通常以签到频率数据的形式显示，这反映了用户对兴趣点的偏好程度。签到交互次数越多，则说明用户越偏好。传统兴趣点推荐模型通常将隐式频率反馈简化为二进制反馈，这在某种程度上导致信息丢失。泊松分解模型[34]用泊松似然代替概率矩阵分解中的常用高斯似然，这保证了潜在因子的非负性。此外，如文献[34]中所指出的，泊松分解模型适用于对频率数据建模，其显示与隐式反馈交互类似的属性。因此，在本文中采用泊松分解模型来建模用户的签到交互行为，并从隐式频率反馈中学习潜在的用户特征和兴趣点特征。

如同文献[7]，基于贝叶斯排序的泊松分解兴趣点推荐模型结合了泊松分解模型和贝叶斯个性化排序，采用成对学习方法来学习用户对于兴趣点之间的偏好排名。具体来说，本文假设用户对兴趣点的偏好随着签到交互次数的增加而增加。该假设意味着三个方面：（1）观察兴趣点的偏好排名高于没有观察到的兴趣点偏好排名；（2）如果观察到两个兴趣点，则用户更偏好基于其签到交互次数较多的兴趣点而不是签到交互次数较少的兴趣点；（3）对于两个没有观察到的兴趣点，本文无法推断出用户对它们的偏好顺序。设rui表示用户u和兴趣点li之间的交互次数，ruj表示用户u和兴趣点lj之间的交互次数。如果rui>0 和ruj= 0，则用户u更喜欢兴趣点li超过兴趣点lj；即li≻ulj，其中≻u表示用户u和兴趣点li和lj之间的偏好关系。如果rui-ruj≥ϖ和ruj>0，则li≻ulj，其中ϖ表示阈值参数。换句话说，如果rui和ruj之间的差异超过阈值ϖ，本文就假设用户对于li的偏好胜过对于兴趣点lj的偏好。形式上，训练集DL（即三元组(u,li,lj)）定义如下：

给定用户u和兴趣点li≻ulj之间的偏好关系，本文最大化后验概率Pr(Ω|≻u)来学习潜在用户和兴趣点特征。Ω表示模型参数；假定所有用户彼此独立，并且还假设特定用户的一个（用户，兴趣点）对的偏好排名独立于其他（用户，兴趣点）对的排名。 同时，基于偏好关系的总体性和反对称性，得到所有用户的似然函数，如下：

其中A(x)是指示函数。假设Pr(li≻ulj|Ω)表示用户u更喜欢兴趣点li超过兴趣点lj的概率，则得到如下公式：

其中ρ(· )是逻辑sigmoid函数。(Ω)是模型参数的实数值函数，捕获用户u，兴趣点li和兴趣点lj之间的关系，定义如下：

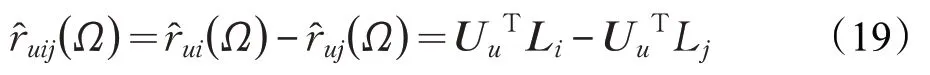
因此，假定潜在用户和兴趣点特征向量的服从Gamma先验分布，根据公式（1）～（4），得到如下公式：

因此，根据公式（5），最大化后验概率的对数，最终得到基于排序的泊松兴趣点模型的目标函数如下：

4.3 HNNCRPFM模型

文献[11]指出预测分数反映了用户对兴趣点的偏好。 图3 是HNNCRPFM 模型架构。因此，基于公式（13），在获得基于正反馈（用户，兴趣点）对和负反馈（用户，兴趣点）对的预测分数（即，和）实数值函数，即根据公式（13）得到：

图3 HNNCRPFM模型架构

本文用泊松分布初始化用户嵌入矩阵U和兴趣点嵌入矩阵L，泊松分布由参数αk和参数βk参数化。在训练阶段，根据训练集DL的构造规则，本文在每次迭代中统一采样三元组(u,li,lj)并控制每个正例的负反馈数量。在对这些采样的三元组进行混洗后，将一批三元组输入到本文的神经个性化排序模型中。对于优化算法，本文采用Adam[37]来更新梯度。

本文提出的推荐算法计算主要消耗涉及两个部分：基于排序的泊松分布和混合神经协同排序模型。

根据文献[8，28]，基于排序泊松分解过程中学习潜在特征向量的计算耗费在于更新目标函数的时间复杂度为O(ζ⋅ι⋅ς)，其中，ζ,ι分别是正采样和负采样的数量，ς是潜在向量的维度。同时，计算一个元组的得分消耗是O(ς)。由于非零观察项的数量非常稀少，学习潜在因子的计算耗费相对于样本数量而言是快速和线性的。因此，每次迭代更新潜在因子的计算耗费为O(ζ⋅ι⋅ς)。

对于混合神经网络协同排序模型而言，文献[33]中基于多层感知器（MLP）作为一种学习非线性用户-项目交互关系的经典神经网络，根据文献[12]的分析，所提出基于MLP 网络的NRPFM 模型的时间复杂度为T(n)=n2。而文献[38]中，提出基于多个叠加的神经网络的隐式反馈个性化成对排序模型，其时间复杂度也为T(n)=n2。而在本文所提出的混合神经网络协同排序模型中，MLP 只是本文所提出的混合神经网络协同排序模型的一部分，在混合神经网络协同排序模型训练过程中，为了优化模型，需要对所有的数据集训练ν次，在每一次训练过程中，都要进入隐藏层进行循环ξ次。则训练过程中的时间复杂度为T(n)=ξ×ν=n2。除了上述步骤，本文提出的模型，还需要对用户未观察到的兴趣点的预测分数进行逐一比较，这里需要循环的次数为每个用户未观察到的项目的数量，最终本文提出的混合神经网络协同排序模型的时间复杂度为T(n)=n3。这也与本文的模型的结构嵌入层、隐藏层和预测层相符合。

5 实验

5.1 实验数据集

本文使用两个公开数据集Foursquare①http://www.ntu.edu.sg/home/gaocong/datacode.htm和Gowalla①来评估本文提出推荐算法的性能。Foursquare（https：//foursquare.com/）和Gowalla（http：//gowalla.com/）是两个受欢迎的基于位置的社交网络（LBSN）。在Foursquare和Gowalla中，用户在兴趣点（例如，餐馆、旅游景点和商店）的签到方面呈现他们的偏好。换句话说，用户通过签到与兴趣点交互，在某种程度上签到的次数表示用户对兴趣点的偏好程度。

在Foursquare 数据集中，所有签到都是在2010 年8月至2011年7月在新加坡内进行的。Gowalla数据集的签到都是在2009年2月至2010年10月在美国加利福尼亚州和内华达州内进行。在这两个数据集中，在少于5个位置签到已被删除，一个用户应该至少访问5个不同的兴趣点。Foursquare 数据集包含来自2 321 个用户的5 596个位置的194 108个签到。Gowalla数据集包括来自5 000 个用户的23 997 个位置的242 172 个签到。Foursquare和Gowalla数据集的稀疏度分别为99.18%和99.86%。显然，Foursquare 和Gowalla 数据集都非常稀疏。在Foursquare 数据集中，每个用户平均签到45.57个位置。在Gowalla，每个用户平均签到了32.13 个位置。Foursquare和Gowalla的具体统计数据如表1。

表1 Foursquare和Gowalla数据集的统计

5.2 实验评估指标

本文使用两个广泛使用的排序度量来评估不同推荐算法的性能，即precisionu@m和recallu@m，其中m是排名推荐列表的长度。 给定用户u，准确度和召回率定义如下：

其中，是用户的top-k推荐兴趣点列表，而是用户u在测试集中的访问兴趣点列表。整个推荐算法的最终准确度和召回率分别通过对所有用户的准确度和召回值进行平均来计算。对于这两个指标，本文设置m=3、5、10来评估本文实验中的性能。

5.3 对比方法

为了证明本文所提出模型的有效性，本文与以下几个主流POI推荐方法进行比较。

（1）用于隐式反馈的传统推荐算法

WRMF[3]：加权正则化矩阵分解，通过基于矩阵分解模型将不同的权值分配为观察到的和未观察到的签到，然后最小化平方误差损失。

BPRMF[28]：贝叶斯个性化排序，它采用BPR的标准来优化了观察和未观察POI的偏好排序，采用逐对的方法来处理OCCF问题。

Rank-PFM[7]：一种基于BPR的泊松矩阵分解POI推荐方法。该方法使用泊松分布建模用户签到行为，用BPR标准优化泊松矩阵分解的损失函数。

（2）基于神经网络的推荐算法

NeuMF[12]：NeuMF是利用深度神经网络基于隐式反馈的推荐算法，它在一个统一的框架中融合了广义矩阵分解和多层感知器从而学习潜在特征，可以同时模拟潜在用户特征和潜在项目特征之间的线性和非线性相互作用。

NRPFM[33]：用于具有隐式频率反馈的协同过滤的神经个性化排序模型，其将基于排序的泊松因子模型与MLP集成。

5.4 实验设置

为了进行公平的比较，在本文的实验中，根据相关文献的参考设定每种方法的最优参数，从而保证每种方法都可以实现最佳性能。同时，采用统一的采样策略来对用户兴趣点对进行采样以进行模型训练。隐藏层作为模型中体现高度非线性相互作用能力的关键，尤其是最后一层隐藏层的大小，能够决定模型的能力。增加隐藏层数可以降低网络误差，提高最终的精度，但也使神经网络复杂化，从而增加了网络的训练时间和出现“过拟合”的倾向。需要根据不同的需求以及场景进行调整，对于不同模型而言，隐藏层的设置也不同。因此，结合文献[12，33]中对应隐藏层的设置和本文5.6.1小节的实验结果。对于BPR，λθ=0.001，对于WRMF 中，λ=0.001，α=1。对于NeuMF，本文采用具有三个隐藏层的神经网络的结构，其中每个隐藏层的大小为（32，16，8）。用户和兴趣点的嵌入大小等于第一个隐藏层的大小，即32。梯度下降超参数学习率和正则化参数分别设定为0.001 和0.001。对于Rank-PFM：αk=1，βk=0.2，k=1，2，…，10。Foursquare上λg=0.1，Gowalla上λg=0.3。对于NRPFM，本文初始化模型参数，αk=2，βk=0.2。其中，依然将隐藏层的数量设置为3，将每个隐藏层的大小设置为（32，16，8）。同时，本文将每个正实例的负样本数设置为8，ϖ=2，并采用批量大小为256的Adam作为优化器。对于HNNCRPFM，批量大小设置为256，学习率设置为0.005，也选择Adam算法来进行优化。采用负采样率为1 进行实验，即对每个正实例采样一个负实例。在HNNCRPFM模型的右边模块部分中，使用四个隐藏层的神经网络，四个隐藏层都使用ReLu 函数作为激活函数。在本次实验中，在右边模块部分中隐藏层的结构是（128，64，32，16）。对于本文中的泊松分解模型，本文使用Gamma分布初始化模型参数，αk=2，βk=0.2，Foursquare上λg=0.1，Gowalla上λg=0.3。对于本文模型的优化过程中使用Dropout 技术，其中Dropout 概率设置为0.5。本文提出的模型是在配置Nvidia GeForce GTX 1080 Ti 显卡的机器上运行PyTorch 实现。实验中，随机选择数据集的20%作为测试数据集，其余80%的数据集作为训练数据集。本文进行5次数据分割，并在每个数据集的测试集上报告平均结果。类似的数据分区方法已被用于以前的工作[11]，以验证推荐的性能。

5.5 性能对比

从图4和图5中，本文得到如下观察结论：

首先，所提出的HNNCRPFM 模型在所有指标中的在两个数据集上比相关主流先进的POI 推荐算法表现的明显更好。具体而言，HNNCRPFM 显着优于传统的方法WRMF、BPRMF 和Rank-PFM。对比这两种基于神经网络的方法（即NeuMF 和NRPFM），HNNCRPFM在Foursquare和Gowalla数据集也是性能领先的。这证明了本文提出模型中混合神经网络的有效性。在捕获非线性用户-兴趣点交互关系时，将基于排序神经网络排序的泊松模型和基于混合神经网络模型进行整合学习用户对兴趣点的偏好的排序模型，能够有效提高推荐性能。原因如下：（1）混合神经网络中，左边模块应用线性网络映射来模拟潜在用户和项目向量的相互作用，右边模块应用非线性的神经网络来模拟特征的潜在结构，通过将它们融合在一起，可以同时获得在线性和非线性捕捉能力的优势；（2）允许左右2 个模块学习单独的嵌入，保证最佳嵌入维数和相关权重，然后通过连接它们的最后一个隐藏层来融合这两个模型，使得最终的预测能力得到了提高；（3）混合神经网络的左边模块是一个仅具有限制能力的浅层学习模型，而右边模块是一个存在过度拟合风险的深层学习模型，将它们融合在一起可以增加模型的容量，同时防止过度拟合。

图4 基于Foursquare数据集的性能对比

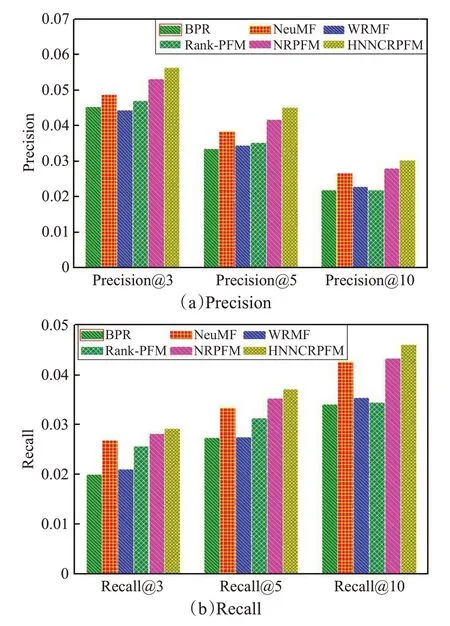
图5 基于Gowalla数据集的性能对比

其次，BPR 在两个数据集上性能最差，因为BPR 仍然依赖于简单的矩阵分解，所以它无法正确获得复杂的潜在用户/项目表示。另外，如何区分负面反馈和未知数，并没有太多关注；BPR 将所有未知因素视为负面反馈。此外，在本文实验中，对于BPR模型采用均匀采样的策略采样用户-兴趣点对训练模型而不是采用单独的采样策略。这样的结论在相关工作[13]中也观察到了相同的现象。相比而言，WRMF与BPR性能相当，一个可能的解释就是WRMF通过给样本正例和样本负例赋值合适的权重，同时逐点的方式可能恰好拟合该数据集中的相关数据分布，但是由于WRMF 无法很好地缓解数据稀疏性问题，而使得其性能依然无法大幅超越BPR。Rank-PFM性能优于WRMF和BPR，该结果表明泊松分解模型比矩阵分解模型更适合于用于隐式频率反馈的建模，同时也更适合建模用户的签到行为，同时将BPR标准与泊松矩阵分解相结合，利用BPR标准来优化了泊松矩阵分解的损失函数，利用未观察到的数据来学习参数可以有效减轻数据稀疏性问题，最终更加准确建模用户隐式反馈信息，取得了不错的性能。

第三，基于神经网络的2 种方法NeuMF 和NRPFM明显优于上述3 种传统方法。这表明非线性提取隐藏的高级特征的对于提升推荐性能的巨大帮助。而NeuMF和NRPFM性能落后于本文所提出的模型，这恰好说明了本文融合了线性的网络层和非线性MLP的混合神经网络具有很高的特征捕捉能力。

总之，实验结果表明，所提出的HNNCRPFM 模型可以成功地学习用户对于兴趣点的偏好，从而导致POI推荐的具有优越的推荐性能。

5.6 相关参数影响

5.6.1 混合神经网络层次的影响

在本文提出的方法中，本文使用混合神经网络从用户的隐式反馈中学习用户和兴趣点特征向量之间的非线性交互。神经网络的深度是影响神经网络表达能力的重要因素。在本节中，本文进行了一组实验来研究神经网络深度对推荐质量的影响。本文将最后一个隐藏层的大小固定为8，并将神经网络的深度从0改为5。例如，如果神经网络的深度为4，则神经网络的结构为8→16→32→64，用户和兴趣点的嵌入大小为64。其他参数保持与5.4节中描述的相同的设置。本文仅在图6中呈现在Foursquare 数据集上实验结果，而在Gowalla 数据集上的实验结果显示出类似的趋势。

图6 基于不同层次的性能对比

HNNCRPFM-n表示具有n隐藏层的HNNCRPFM模型。从图6 可以看出，虽然HNNCRPFM-2 只有比HNNCRPFM-1 多一个隐藏层，但它的性能好于HNNCRPFM-1。在Foursquare数据集上，当层数小于3时，增加隐藏层的数量会带来更好的性能；当本文使用具有超过3 个以上隐藏层的HNNCRPFM 时，性能不会提高。该结果表明简单地连接潜在载体不足以捕获潜在因子之间的相互作用。另外可能的原因是更深的神经网络使得HNNCRPFM具有更多可训练的参数，这些参数在训练数据有限的情况下相对难以学习，导致推荐性能的下降。

5.6.2 参数 αk 和 βk 的影响

在本文提出的方法中，参数αk和βk用于初始化用户嵌入矩阵和兴趣点嵌入矩阵。固定βk=0.2，通过改变的值αk从1到5，观察HNNCRPFM模型的性能变化；同时给定αk=2，改变βk值从0.1到0.5，观察HNNCRPFM模型的性能变化。HNNCRPFM 基于Foursquare 数据集，不同αk和βk的结果分别展示在图7和图8。

图7 αk 的影响

图8 βk 的影响

可以看到，αk和βk都显著影响了本文提出的推荐模型的性能。具有固定值2 的αk的情况下，当βk约为0.2时，HNNCRPFM表现最佳，进一步减小或增加βk的值导致更差的性能。在将βk的值固定为0.2的情况下，HNNCRPFM 显示出类似的趋势；即，当αk超过某个阈值时，所有评估指标首先开始提升然后开始下降。该观察结果表明HNNCRPFM 对用户嵌入矩阵和兴趣点嵌入矩阵的初始化也很敏感，过大或者过小的αk和βk都会影响最终的推荐性能。

6 结束语

在本文中，本文提出了一个基于混合神经网络与基于排序泊松分解模型结合的兴趣点推荐模型，名为HNNCRPFM。HNNCRPFM 首先通过基于贝叶斯技术和泊松分解模型结合构建一个基于排序的泊松分解模型来建模用户对于兴趣点的偏好，与此同时，提出了一种基于混合神经网络的协同排序算法来进一步扩展上述排序学习，然后基于统一推荐模型将上述2种算法融合提供推荐服务。该算法针对隐式反馈数据，改善了上述基于排序泊松分解模型中的相关方法，缓解了类不平衡和数据稀疏性问题，避免了有效信息的丢失；并且通过结合点积网络层和神经网络中的多层感知器两种结构来学习用户与兴趣点的交互。两个真实世界数据集的实验结果表明，所提出的HNNCRPFM在准确率和召回率方面优于现有的先进主流兴趣点推荐模型。作为未来的工作，本文计划将相关注意机制引入HNNCRPFM以获得更好的推荐准确性。