模糊序列感知哈希

王 振，孙福振，张龙波，王 雷

山东理工大学 计算机科学与技术学院，山东 淄博 255000

1 引言

传统图像近邻检索算法根据图像的高维浮点特征描述子（如320 维的全局特征描述子GIST）之间的欧式距离衡量图像之间的相似度，计算复杂度较高，无法实时响应海量图像的近邻检索请求。为了解决这一问题，人们提出利用哈希算法将高维浮点特征映射成紧凑二值编码，并依据汉明距离检索近邻点，其可直接利用计算机硬件指令异或操作计算汉明距离，计算速率较快，并且按位存储二值编码，存储空间利用率较高。

近年来，为了提升近邻检索性能，人们提出了不同种类的哈希算法。王妙等人[1]在神经网络层中加入了哈希层，可实现分级检索策略，其先利用哈希码得到粗检索结果，然后再根据图像高层语义特征之间的欧式距离进行精检索，从而避免了检索复杂度高以及内存不足的问题。朱命冬等人[2]将LSH 算法应用到二元混合类型数据（图像-文本数据）的近邻检索任务中，提出利用LSH 构建能有效融合两种数据类型的相似性的混合索引，并将其用于最近邻查询。为了克服语义信息未被充分利用的局限性，段文静等人[3]提出在一个深度网络框架内同时利用成对标签信息和分类信息学习哈希编码。为了适应分布式存储数据的近邻检索需求，基于乘积量化的分布式哈希学习方法SparkPQ提出在Spark分布式计算框架下利用分布式乘积量化算法学习分布式数据的哈希编码[4]。

根据训练过程是否依赖于数据集，可将现有哈希算法大致分为数据独立哈希与数据依赖哈希。数据独立哈希，如局部敏感哈希[5]，随机生成线性哈希函数，并根据数据点与线性哈希函数的映射符号生成二值编码。由于局部敏感哈希的训练过程不依赖于训练数据集，为了获取较优的近邻检索性能，所生成的二值编码应足够长。之后，为了确保采用紧凑二值编码也能获得令人满意的近邻检索结果，人们提出了数据依赖哈希，其利用机器学习机制，生成符合数据集分布特性的哈希函数。谱哈希[6]（Spectral Hashing，SH）和锚图哈希[7]（Anchor Graph Hashing，AGH）建立了数据点之间的相似性图，并通过分割谱图生成数据点的二值编码，但其要求数据集服从均匀分布。迭代量化[8]（Iterative Quantization，ITQ）哈希建立了超立方体，旨在将超立方体顶点附近的样本映射为相同的编码。类似的，K-均值哈希[9]也将编码中心点附近的数据点映射为相同的二值编码，但其要求编码中心点能够同时最小化量化误差和相似性误差，从而确保编码中心点能够适应于数据集的分布特性。谱哈希[6]、锚图哈希[7]、迭代量化哈希[8]和K-均值哈希[9]旨在将相似或相同的样本映射为相近或相同的二值编码，其适用于语义相似性检索任务。

相对而言，近似近邻检索任务更加关注数据点之间的相对相似性。为此，人们提出了序列保持哈希[1，10-11]，要求在汉明空间内保持数据点之间的原欧式序列关系。最小损失哈希[10]定义了铰链损失函数，惩罚汉明距离较大的相似数据点或汉明距离较小的非相似数据点。与最小损失哈希[10]类似，铰链损失哈希[11]也利用三元组之间的相似性关系近似序列损失。三元损失哈希[12]要求相似数据点之间的汉明距离值应远小于非相似数据点之间的汉明距离值。序列保持哈希[13]（Order Preserving Hashing，OPH）根据数据点与查询数据点之间的距离，将其分成不同的类，并力求在汉明空间和欧式空间内同时最小化类间与类内误差，从而可确保在汉明空间内保持数据点之间的原序列关系。为了进一步增强序列保持性能，序列约束二值编码[1]建立了基于四元组的序列保持约束条件，要求任意四元组在汉明空间和欧式空间内具有相同的序列关系。

通常，上述语义哈希和序列保持哈希认为所有比特位具有相同的权重值，且汉明距离为离散整数值，使得一些编码不同的数据点与查询数据点之间具有相同的汉明距离[4，13]。如编码为“01”和“10”的数据点与编码为“00”的数据点之间的汉明距离均为1，从而无法正确区分这些数据点在近邻检索中的排序。为了解决这一问题，人们提出比特位加权算法，根据比特位的重要程度为其赋予不同的权重值，并根据加权汉明距离进一步区分汉明距离相同的数据点之间的相似度。QaRank 算法[14]根据数据点之间的加权汉明距离和欧式距离，将数据点分成不同的类别，并要求最小化类内与类间误差，且同时保持各个类之间的相对相似性关系。查询敏感比特位权值算法[15]（QsRank）根据原始浮点数据以及近邻半径计算比特位权值，其能有效提升主成分分析哈希的近邻检索性能。加权汉明距离算法要求比特位权值应符合训练数据集的分布特性，且对查询数据点较敏感。与上述比特位权值算法不同，本文所提出的模糊序列感知哈希直接利用二值编码本身的信息区分具有相同汉明距离的数据点对之间的相似度，如图1所示。为了保证所生成的二值编码能够满足近邻检索任务的需求，定义了类似于平均准确率的序列保持约束条件，但仍会有编码不同的样本共享相同的汉明距离，且无法正确区分它们的序列关系，如近邻检索结果（e）所示。为了解决这一问题，在训练阶段中引入首位区分规则，并学习满足这一规则的哈希函数，从而可在近邻检索结果中利用此规则区分汉明距离相同但编码不同的数据点对之间的相似度，使得近邻检索结果唯一，且性能较优，如检索结果（f）所示。

图1 模糊序列感知哈希算法流程图

本文的创新点如下：

（1）提出首位区分规则，依据二值编码本身信息区分模糊序列，与传统比特位权值算法相比，在近邻检索过程中无需额外计算比特位权值与加权汉明距离，降低了近邻检索过程的复杂度。

（2）建立了类似于平均准确率的目标函数，其属于序列保持约束条件，可确保所生成的二值编码能够满足近邻检索任务需求。

（3）提出了二值编码、汉明距离和判断函数的连续化松弛策略，从而可直接采用批量梯度下降算法优化目标函数。

2 模糊序列感知哈希

2.1 首位区分规则

基于哈希的图像近邻检索算法[3，8]主要包含两个步骤，其先生成图像的浮点特征（如全局特征描述子GIST），再利用哈希函数H(x)={h1(x),h2(x),…,hM(x)}将浮点特征映射成M位二值编码B={b1,b2,…,bM}。从而，可根据浮点特征对应的二值编码之间的汉明距离检索图像近邻。hm(x)表示第m位哈希函数，其常被定义为线性函数hm(x)=wTm x，wm为哈希函数hm(x)的系数。bm(x)表示第m位比特编码，其值由数据点x与线性哈希函数hm(x) 的映射符号决定，即bm(x)=sgn(hm(x))。

通常，认为所有比特位的重要程度是相同的[1，9]，且汉明距离为离散整数值，导致一些编码不同的数据点与查询数据点之间具有相同的汉明距离，从而无法准确区分它们在近邻检索结果中的排序[15-16]，并且不同序列的近邻检索性能差异较大。如图2所示，数据点被映射为3 bit 的二值编码，样本a 的编码为“000”，样本b、c、d 的编码分别为“011”“101”“110”。在欧式空间内样本 b 为样本a 的真正近邻点，但在汉明空间内检索样本a 的近邻点时，样本b、c、d 与样本a 之间的汉明距离均为2，它们在汉明空间内的排序是随机的，将产生多种不同的近邻检索结果，并且根据近邻检索性能评价指标，只存在一种最优的近邻检索结果。

图2 模糊序列导致多种不同近邻检索结果

为了解决上述模糊排序问题，可利用比特位权值算法[15-16]根据比特位的重要程度或区分度，赋予每个比特位相应的权重值，从而可根据加权汉明距离进一步区分汉明距离相同的数据点之间的近邻排序。然而，比特位权值算法需要额外学习比特位权值函数，并且在检索过程中需要计算加权汉明距离，增加了训练和检索过程的计算复杂度。

在本文中，提出直接借助二值编码自身的信息区分模糊排序。在近邻检索结果中，若有多个数据点与查询数据点具有相同的汉明距离，则依次比较这些样本点与查询数据点的编码，并优先返回最先出现不同值的样本。若有多个样本同时出现不同值，则继续依次比较剩余位，直至能够正确区分所有样本的近邻排序。例如，对于图2 中的模糊序列，可定义比较顺序为从右至左，样本b、c与样本a在第1位具有不同的编码，二者在近邻检索结果中的排序应在样本d 之前。但此时仍无法正确区分样本b、c 之间的排序，则继续依次向后比较，样本b 与样本a 在第2 位具有不同的编码，因此优先返回样本b。最终，可得到样本a 的近邻检索结果为b、c、d。综上，首位区分规则能够区分汉明距离相同但编码不同的样本在近邻检索结果中的序列。

基于首位区分规则的比特位权值算法与传统加权算法均赋予比特位不同的权重值，并根据加权汉明距离检索近邻点。传统加权算法在近邻检索过程中需要考虑所有比特位的值，其近邻检索复杂度为O(M)，M为数据点被映射为二值编码的长度。相对而言，当首次出现值不相同的比特位时，基于首位区分规则的近邻检索算法便可有效区分数据点在近邻检索结果中的相对排序，其近邻检索时间复杂度仅为O(lbM)。

首位区分规则要求，若数据点的第1 至m-1 位的比特值相同，则第m位具有优先决定权，即第m位的权重值应大于之后所有比特位的权重值之和，其形式化定义如公式（1）所示：

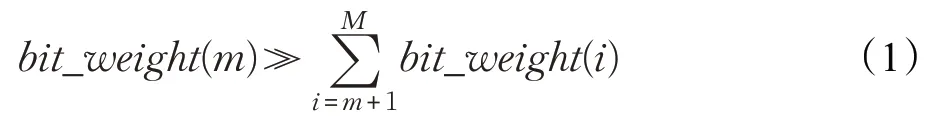
bit_weight(m)表示第m位比特位的权重值。为了保证比特位权重值能够满足公式（1）所定义的约束条件，比特位的权重值应呈指数幂增长。每个比特位的最大取值为1，为了保证计算加权汉明距离时在任意比特位上均不产生溢出，需将指数幂的底数设定为大于2的数值。在本文中，利用梯度下降算法优化目标函数，为了方便计算加权汉明距离的导数，幂指数的底数取值为10。综上，可预先定义第m位比特位的权重值为eM-m，并采用公式（2）定义基于首位区分规则的加权汉明距离。

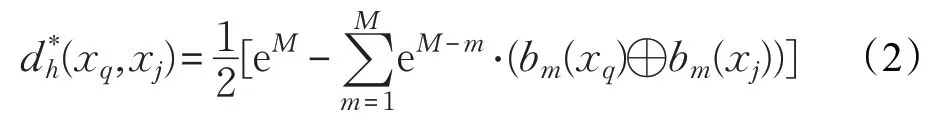
接下来，要解决的问题是如何保证采用首位区分规则能够得到较优的近邻检索结果。

2.2 序列保持约束

语义相似性保持哈希[7-8]强调将相似数据点映射为相同或相近的二值编码，其适应于语义相似性检索任务。相对而言，近邻检索任务更强调数据点之间的相对相似性关系。因此，为了在汉明空间内得到较优的近邻检索性能，需建立序列保持约束目标。类似的，三元损失哈希[12]、铰链损失哈希[11]和最小损失哈希[10]定义了基于三元组的序列保持约束，序列约束哈希[1]学习满足基于四元组的序列保持约束条件的二值编码。

在本文中，为了进一步增强序列保持性能，定义了类似于近邻检索性能评价指标平均准确率（Average Precision，AP）的约束条件AP*，其要求在汉明空间内每一个截断k处得到的查询样本xq的近邻点与原欧式空间内的近邻检索结果是一致的，如公式（3）所示：

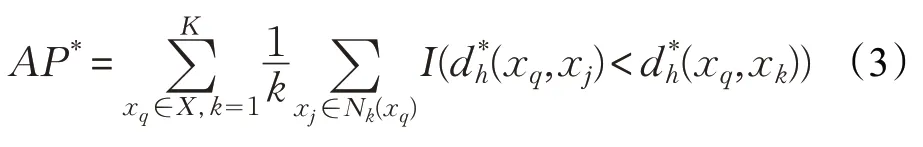
X为训练数据集，Nk(xq)为欧式空间内查询数据点xq的k近邻集合，xj表示第j(j≤k)个近邻数据点。I(·) 为判断函数，要求(xq,xj) 之间的汉明距离应小于(xq,xk)之间的汉明距离，若条件满足，返回1，否则，返回0。在公式（3）中，采用2.1 节中定义的首位区分规则计算汉明序列公式（3）强调，返回不同数量 (k)的近邻样本，均具有较优的检索准确率，其属于序列保持约束条件，可保证得到较优的近邻检索性能。

在本文中，采用批量梯度下降算法学习哈希函数。故而，将目标函数定义为公式（4）所示：

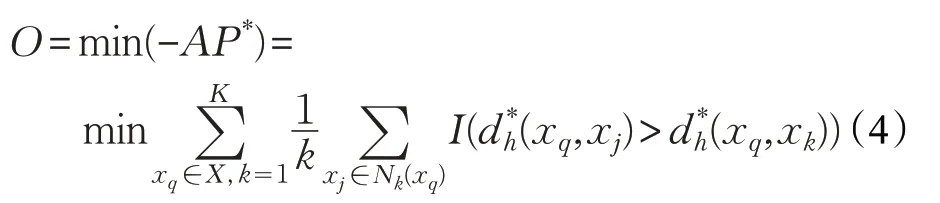
2.3 松弛优化

公式（4）所定义的目标函数中含有二值编码、汉明距离和判断函数，其均为离散整数值，若直接采用批量梯度下降算法优化原目标函数，其为NP难问题。因此，需要对二值编码、汉明距离以及判断函数做连续化松弛处理。

对于二值编码过程，可采用tanh（·）函数近似替代其中的符号函数，如公式（5）所示：

结合公式（5），可采用公式（6）重新定义基于首位区分规则的汉明距离：

在本文中，利用公式（7）近似替代原目标函数中的判断函数I(⋅)：

函数G(⋅)的定义如公式（8）所示：

在训练阶段，分别利用公式（5）、（6）和（7）替代原有的二值编码、汉明距离和判断函数。采用批量梯度下降算法学习哈希函数hm时，目标函数关于哈希函数系数wm的偏导数，如公式（9）所示：

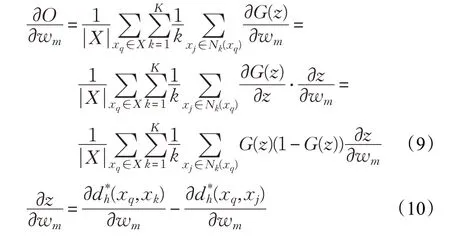
数据点之间的汉明距离关于wm的偏导数如公式（11）所示：

在训练过程中，采用公式（12）更新哈希函数的系数，参数λ为更新速率。

当8-点关联一个3-面时,类似于对7度点的讨论,我们可以得出类似最坏情形，即在最坏情况下是8-点关联着(3,3,8)-面,三面及面上的点最多从8-点拿走的权值为同理,对于9+-点也满足同样的结果，分别称之为最坏3-面8-点情形和最坏3-面9+-点情形。

综上，模糊序列感知哈希的伪代码如算法1所示。

算法1模糊序列感知哈希

输入：数据集X；编码长度：M

输出：哈希函数的系数：W={w1,w2,…,wM}

1.随机初始化W={w1,w2,…,wM}

2.将数据集X分成多个子集{X1,X2,…,Xn}

3.Fori=1:n

5.WhilexqinXi

6.采用首位决策规则计算xq在汉明空间的近邻序列

7.利用公式（9）计算目标函数对wm的偏导数

8.利用公式（12）更新wm的值

9.Until Convergence

10.End

11.End

在算法1中，采用随机批量梯度下降算法迭代更新线性哈希函数。全部训练数据被分成n个子集，且每个子集中含有L个数据点。在每次迭代更新中，力求最小化数据点在欧式空间与汉明距离内的序列误差。本算法在线下预先计算数据点之间的欧式序列关系，线上训练时只需计算每个子集中数据点的基于首位区分规则的汉明近邻序列，每个子集中含有L个数据点，其时间复杂度为O(LlbM)。在每个批次中，共需进行L次更新，学习M个线性哈希函数，且全部数据被分为n个子集。综上，算法1的训练时间复杂度为O(M⋅n⋅L2⋅lbM)。

3 实验

3.1 实验设置

在本文中，分别在三种图像数据集上设置了近邻检索对比实验，三种数据集分别为NUS-WIDE[17]、22K LabelME[18]和ImageNet 100。在近邻检索实验中，每种数据集均被分为三部分，训练数据集、待查询数据集和测试数据集。

NUS-WIDE数据集[17]包含27万Flickr图像，从中分别随机选取19 万幅和5 万幅图像作为待查询数据集和测试数据集，并且训练数据集包含5 万幅图像。22K LabelMe数据集[18]为不含标签的图像集，共包含2.2万幅图像，从中随机选取2 万幅图像作为待查询数据集，其余2 000幅图像作为测试集，并从中随机选取5 000幅图像作为训练数据集。ImageNet 100 是ImageNet 图像集的子集，共包含100 类图像，随机选取13 万幅图像作为待查询数据集，3万幅图像作为训练数据集，1万幅图像作为测试数据集。

在本文中，分别采用召回率（recall）和平均均匀准确率（mAP）评价近邻检索性能。召回率的定义如公式（13）所示，其表示检索到的正样本的数量占所有正样本数量的比重，#（检索到的正样本）表示检索到的正样本的数量，#（正样本）表示数据集中所有正样本的数量。然而，召回率无法衡量正样本的返回速率。为此，将进一步采用平均均匀准确率衡量近邻检索性能，其定义如公式（14）所示，|Q|表示查询样本的数量，Kn表示第n个样本的真实近邻点的数量，rank(j)表示第j个正样本在查询结果中的排序，由此可知，正样本返回速率越快，其值越大。

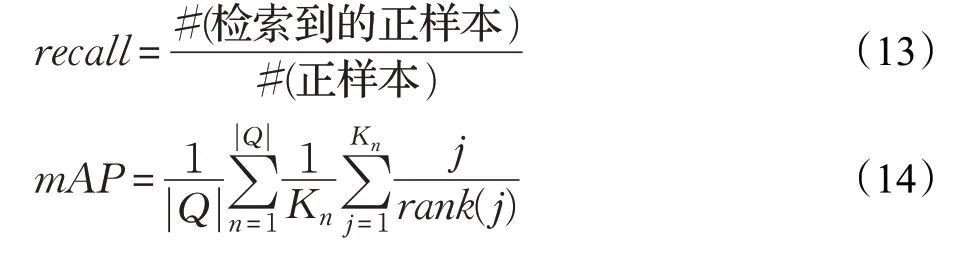
3.2 实验结果与分析

在近邻检索对比实验中，先提取NUS-WIDE[17]、22K LabelMe[18]、ImageNet100 图像集的 GIST 特征描述子，然后采用不同种类的哈希算法分别将图像的GIST特征映射为32位、64位二值编码，并根据汉明距离检索近邻点，其实验结果如图3～5 和表1～3 所示。在召回率曲线图中，横坐标为返回的近邻点数量，纵坐标为召回率，M表示二值编码长度，NN表示在原欧式空间内真正近邻点的数量。

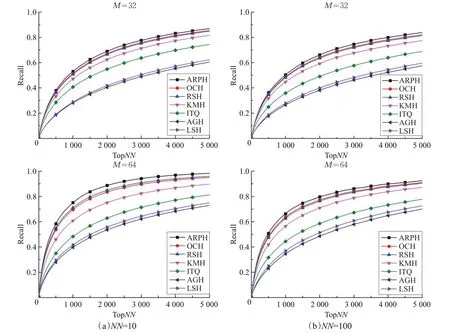
图3 在22K LabelMe数据集上的近邻检索性能召回率曲线

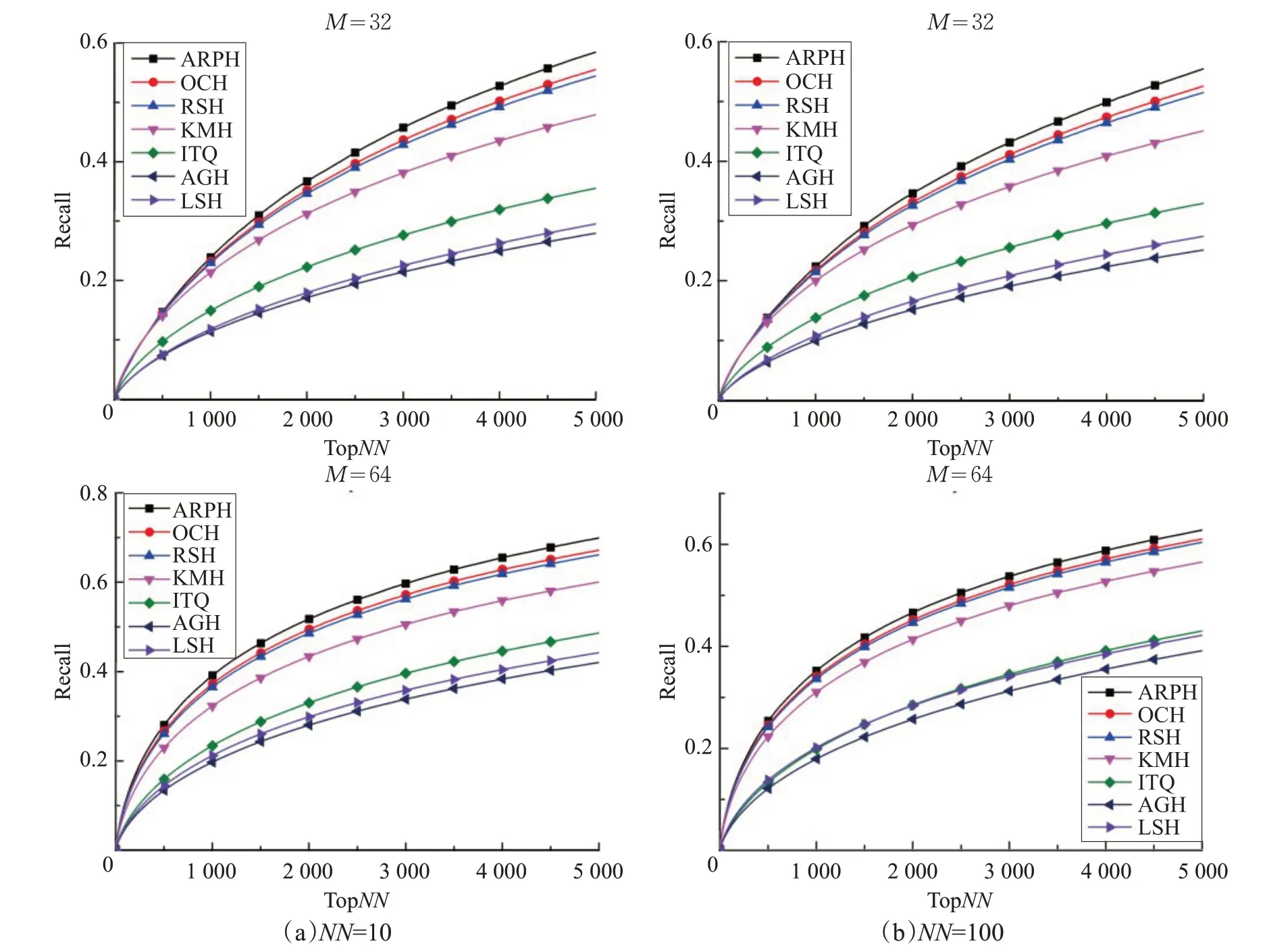
图4 在NUS-WIDE数据集上的近邻检索性能召回率曲线

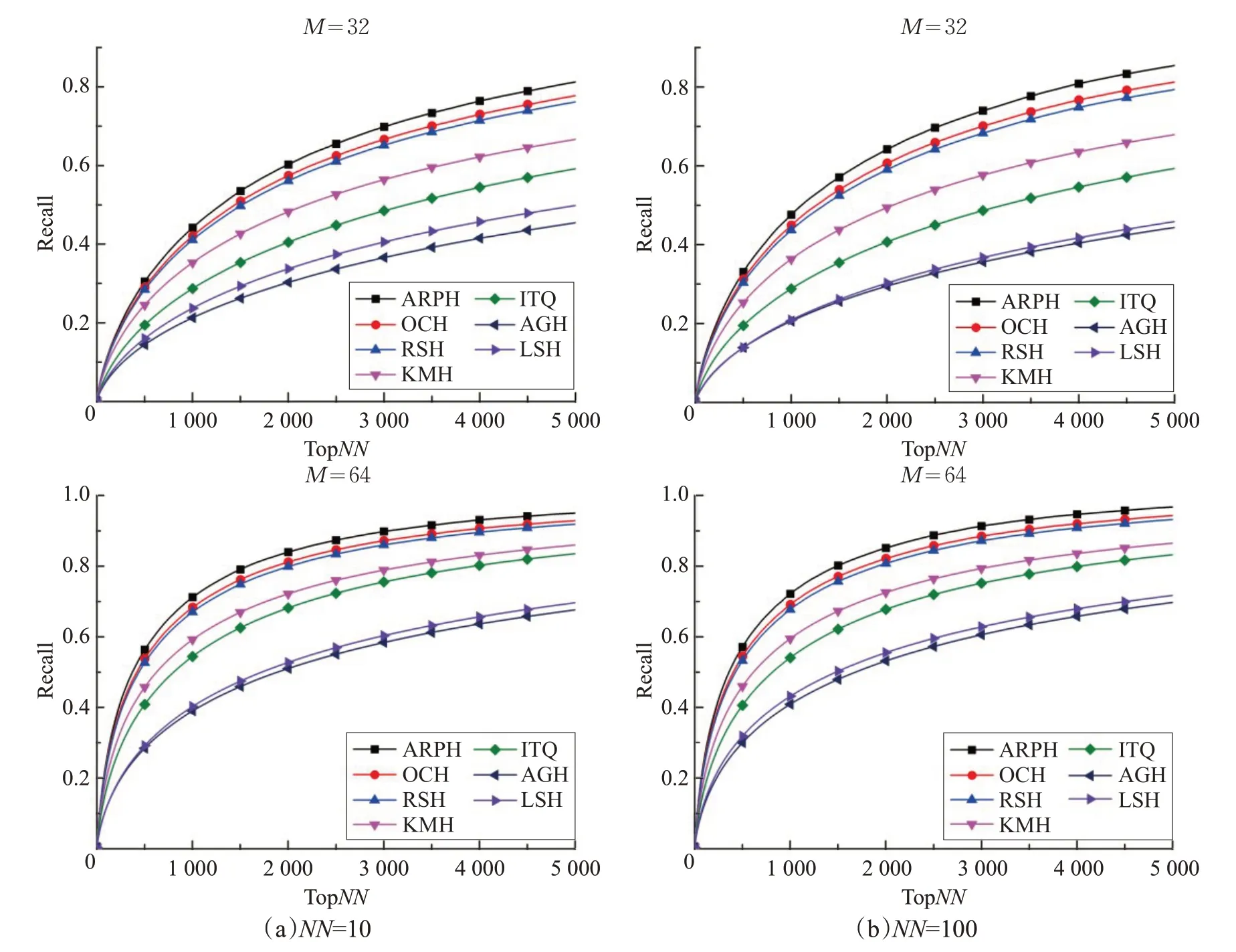
图5 在ImageNet 100数据集上的近邻检索性能召回率曲线

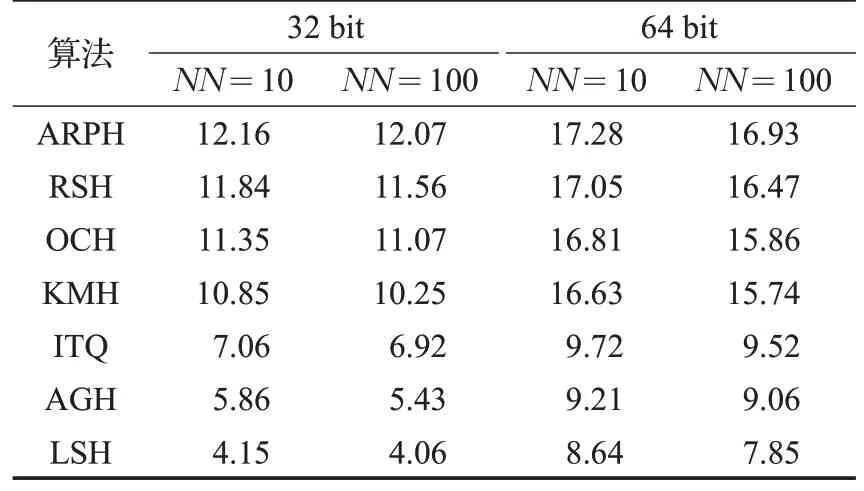
表1 在22K LabelMe数据集上的平均均匀准确率值 %

表2 在NUS-WIDE数据集上的平均均匀准确率值%

表3 在ImageNet 100数据集上的平均均匀准确率值 %

局部敏感哈希[5]（LSH）随机生成线性映射函数，训练过程不依赖于数据集，近邻检索性能不能随着编码长度的增加而显著提升，且本文所采用的均是紧凑二值编码，故而局部敏感哈希[5]的近邻检索性能相对较弱。锚图哈希[7]（AGH）采用K均值算法学习数据集的锚点，并通过分割锚点之间的相似性谱图生成数据集的二值编码，以确保相似数据点被映射为相同编码，其近邻检索性能优于局部敏感哈希算法。锚图哈希要求数据集服从于均匀分布，而本文所采用的真实数据集并不符合均匀分布，故而锚图哈希的近邻检索性能仍相对较弱。迭代量化（ITQ）哈希[8]、K均值哈希[9]（KMH）、铰链哈希[11]（RSH）、序列约束哈希[1]（OCH）以及模糊序列感知哈希（ARPH）不再要求训练数据满足特定的分布特性，近邻检索性能优于锚图哈希。迭代量化哈希[8]将相似或相近的数据点映射至同一个正立方体顶点，并赋予相同的二值编码。在迭代量化哈希算法中，正立方体的顶点是固定的，对数据集分布特性的自适应能力较弱。相对而言，K均值哈希[9]（KMH）学习能够同时最小化相似性误差和量化误差的顶点，使得编码中心点与数据集的分布特性相符，故K均值哈希的近邻检索性能要优于迭代量化哈希。K均值哈希[9]、迭代量化哈希[8]、锚图哈希[7]以及局部敏感哈希[5]只关注数据点之间的相似性保持问题，而近邻检索算法更重视数据点之间的相对相似性。铰链损失哈希[11]建立了基于三元组之间的相对相似性保持约束条件，序列约束保持哈希[1]建立了基于四元组之间的相对相似性保持约束条件。模糊序列感知哈希建立了类似于均匀准确率的目标，要求在每一个截断k处，在汉明空间与欧式空间内得到的近邻检索结果是相同的，其属于序列保持约束。从而可知，铰链损失哈希[11]、序列约束保持哈希[1]以及模糊序列感知哈希关注如何保持数据点之间的序列关系，更适应于近邻检索任务，性能相对较优。但是，铰链损失哈希与序列约束保持哈希未关注近邻检索中的模糊序列问题，对于与查询数据点具有相同汉明距离的数据点，采用随机排序的规则，使得算法性能的稳定性较差。模糊序列感知哈希定义了首位区分规则，并学习满足这一规则的序列保持二值编码，从而可有效区分近邻检索中的模糊序列，算法性能较稳定。在三种大型图像数据集上的近邻检索实验也证明了，模糊序列感知哈希具有较优的近邻检索性能。

4 结束语

基于哈希的图像近邻检索算法将图像高维浮点描述子映射成二值编码，并在汉明空间内检索图像近邻，其具有响应速率快、存储空间小的优势，已经得到广泛应用。一般哈希算法认为所有比特位具有相同的权重值，且汉明距离为离散整数值，从而使得编码不同的数据点与同一查询数据点具有相同的汉明距离，这将导致序列模糊问题。为了解决这一问题，本文提出了首位区分规则，优先返回最早出现不同比特值的数据点，并在训练过程中学习满足首位区分规则的哈希函数，从而可直接根据二值编码本身的信息区分模糊序列。与比特位权值算法相比，无需额外计算比特位权值与加权汉明距离，查询复杂度相对较低。学习哈希函数时，定义了类似于均匀准确率的约束目标，其属于序列保持约束条件，可确保在汉明空间内得到较优的近邻检索性能。在训练过程中，对符号函数、判断函数以及汉明距离均做了松弛连续化处理，从而可利用随机梯度下降算法学习满足目标约束条件的哈希函数。在三种图像数据集上的近邻检索对比实验也证明了，本文所提哈希算法具有较优的近邻检索性能。