采用异形剪力键的钢空腹夹层板静力试验研究

沈睿麟，肖建春*，马克俭，王 琴，毛家意, 卢 杨

(1.贵州大学 空间结构研究中心，贵州 贵阳 550003 ；2.贵州省结构工程重点实验室，贵州 贵阳 550025; 3.贵阳市人民防空办公室，贵州 贵阳 550003; 4.贵州师范大学 校党委组织部，贵州 贵阳 550025)

贵州大学空间结构研究中心马克俭院士提出的钢空腹夹层板盒式结构[1]由于其良好的经济性和综合力学性能，已经广泛应用于公用及工业建筑中[2-3]。

盒式结构体系由钢空腹夹层板和网格式墙架[4]组成。其中钢空腹夹层板由上部的钢筋混凝土板和下部由剪力键和上下肋共同组成的钢架组成，混凝土板与钢架之间一般采用栓钉作为抗剪连接件[5]。钢空腹夹层板按照空间布局可分为正交正放[6-7]、正交斜放[8-9]和蜂窝型[10-11]等形式。

剪力键是钢空腹夹层板的重要组成部分，其研究一直是重点和热点。刘卓群[12]通过有限元分析得出设置外部加劲板可以有效降低剪力键的应力，提升钢空腹夹层板的整体承载力。尚洪坤和白志强分别设计了全尺寸的剪力键试件，通过剪切试验表明通过设置外部加劲板对剪力键的抗剪刚度有明显的提升[13-14]。韦东阳在方钢管剪力键内部设置内部加劲板(图1(a))，通过有限元分析得出设置内部加劲板能有效地降低剪力键的应力，方钢管的受拉变形也有明显改善，水平位移减小了50%[15]。

由于设置内部加劲板的剪力键施工难度较大，对其构造进行了优化设计，提出了采用带翼缘的十字型剪力键的钢空腹夹层板结构(简称异形剪力键)，申请了国家专利并获得了专利授权[16]。该异形剪力键与上下肋、盖板的连接构造如图1(b)所示。

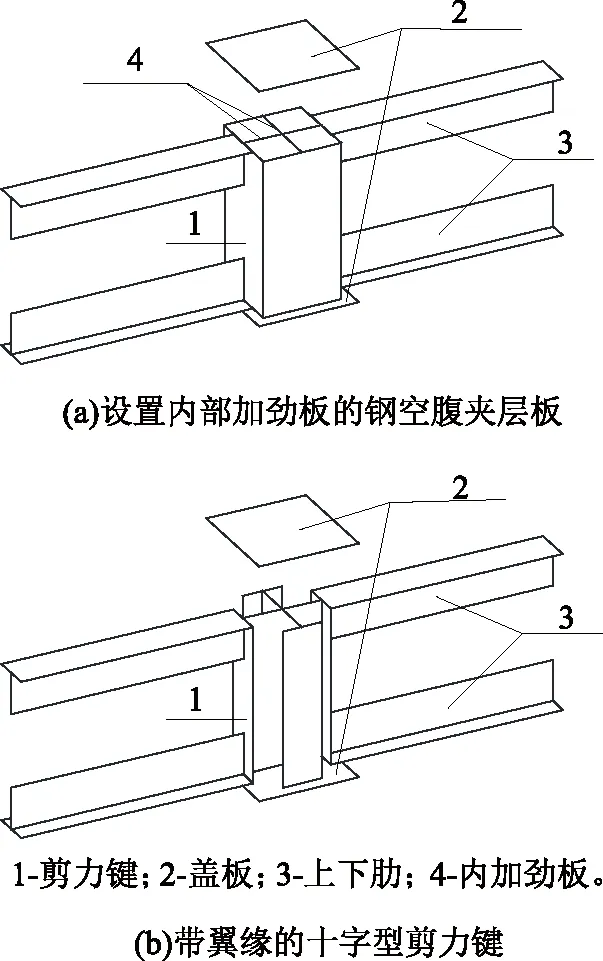
图1 剪力键节点构造Fig.1 Joint construction of shear key

在之前的研究中，对未浇筑混凝土板的采用异形剪力键的钢空腹夹层板进行了分级静力加载试验，通过与理论分析方法——拟交叉梁系法及有限元计算结果的对比得到：在弹性范围内3种方法均具有较高的精度[17]。 本文继续在钢空腹夹层板上部浇筑混凝土并构成钢空腹夹层板组合结构，进行静力加载试验，测量挠度和应变等数据，与有限元的计算结果进行对比。

1 试验概况

1.1 模型结构设计

综合考虑试验场地、经费、可供购买的型钢及钢空腹夹层板的构造要求等因素，设计的试验模型如图2所示：网格尺寸为1 m×1 m，设计为长宽比为5∶1的单向受力体系，受力方向为5个网格，即整体网格尺寸为5 m×1 m，钢筋混凝土板厚0.1 m，混凝土板超出剪力键中心线150 mm，超出剪力键边缘为50 mm。即混凝土板尺寸为5.3 m×1.3 m×0.1 m。剪力键高0.2 m，剪力键截面尺寸如图2(c)所示，翼缘厚7 mm，宽75 mm，腹板厚5 mm，宽150 mm，与上下两块□200 mm × 200 mm × 8 mm的钢盖板焊接为一个独立的剪力键单元。剪力键单元之间采用长0.85 m，截面为T75 mm × 75 mm × 7 mm × 5 mm的T型钢焊接成一个空间协同工作的钢架。钢架与混凝土板之间用Φ13的栓钉作为抗剪连接件，栓钉如图2(d)所示间距为150 mm，采用单排布置[18]。在钢架上支模、铺设钢筋并浇筑混凝土。考虑到后续试验的要求，钢筋采用双层双向布筋，并在角部设置阳角放射筋，混凝土板挑出T型肋部分非受力方向设置分布筋，分布筋采用Φ4铁丝代替钢筋。将整个模型直接放置于Φ60的圆钢上组成弧形支座。混凝土设计强度为C25，按75～90 mm坍落度进行配比，重量配比为水泥∶砂∶石∶水=1∶1.92∶3∶0.6[19]。钢筋选用HPB300级钢筋，型钢为Q235钢。图3为该模型的施工现场照片。

1.2 测点布置

由于结构的对称性，如图4所示，仅在1/4结构范围内布置测点。其中A、B测点采用德国SICK公司AOD5-N1激光位移传感器进行采集，两测点位于剪力键盖板中心的正下方；C、D、E测点采用WBD 型百分表式位移传感器来测量结构的位移，测点位于每一跨混凝土板底的中心点位置。应变测量点1～2、9～12、19～22号位于异形剪力键的腹板上；其余应变片贴在T型肋的腹板上。所用的应变片均为120-5AA免焊接单向应变片，方向为结构的长轴方向。

图2 几何尺寸/mmFig.2 Geometrical dimensions/mm

图3 模型施工现场Fig.3 Construction site of model

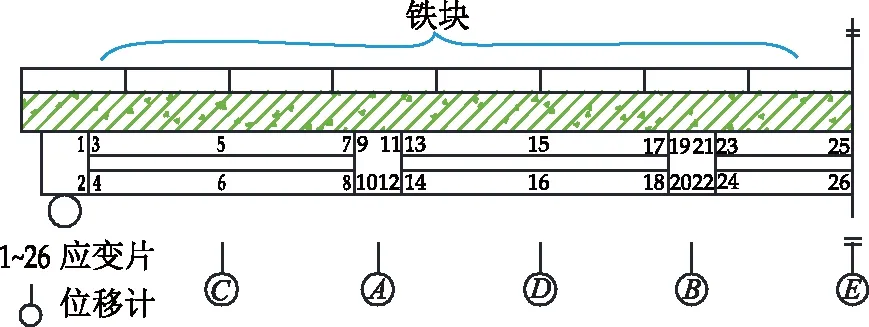
图4 测点布置Fig.4 Measurement points arrangement

1.3 加载方案

本试验采用铁块模拟均布荷载，每块铁块20.4 kg，计为0.2 kN/块，满布共计5×16=80块，合计16 kN。加载区域为5.3 m×1 m，等效荷载为3.0 kN/m2。加载前先将激光位移采集系统和应变采集系统平衡归零后开始采集数据。加载过程如图5所示，放置铁块后静置30 min，停止数据采集后卸载，完成整个静力加载试验。

图5 加载Fig.5 Loading

1.4 试验结果及分析

在加载过程中，混凝土未发现开裂、破坏现象，钢结构上下肋和剪力键均未出现局部屈曲及焊缝开裂现象。在加载到设计荷载之前，应变和位移有规律地均匀增加，各测定的最大应变未超过所用材料的屈服应变，表明在设计荷载下，整个结构均处于弹性工作阶段。

2 有限单元法

该试验选用大型有限元软件ANSYS19.0进行建模计算。SHELL181单元模拟剪力键和T型肋，网格大小为12.5 mm，构件之间焊接牢固，采用共节点的方式进行连接。混凝土使用SOLID65单元、钢筋选用LINK180单元，混凝土和钢筋的网格大小均为50 mm，两者之间直接进行共节点建模。混凝土板与型钢之间不考虑相对滑移，故实体单元与壳单元之间采用绑定接触连接。钢材和钢筋均选用双线性等向强化模型(bilinear isotropic, BISO)，混凝土选用多线性等向强化模型(multilinear isotropic, MISO)进行建模[20]。

由于钢空腹夹层板如图6所示为直接放置在圆钢上组成弧形支座，接触仅为一条直线，模型的边界条件为角部剪力键下盖板的中线上施加一个UZ方向的约束，不约束平动和转动。试验设计为3.0 kN/m2的均布荷载，建模时直接将3.0 kN/m2的面荷载(pressure)施加到混凝土板的表面，有限元模型如图7所示。

图6 支座Fig.6 Support

图7 有限元模型Fig.7 FE model

3 有限元与试验结果对比

3.1 挠度

图8为设计荷载作用下各测点挠度实测值的中位数和有限元理论值的比较，其中A、B点在十字形剪力键下盖板的底部中心，C、D、E位于混凝土板下表面的中心点。所有测点两者的误差均在5%以内，其中C点的误差最大，为4.27%，B点最为接近，误差为0.15%，说明实测值与有限元的拟合度很高。

图8 挠度Fig.8 Deflection

3.2 应变

图9为设计荷载作用下应变的试验采集值的中位数与有限元计算值的对比图。其中(a)、(b)图为第一跨，(c)、(d)图为第二跨，(e)、(f)图为中间跨；1、9、2、10、11、19、12、20、21、22点在十字形剪力键的腹板上，其余点位于T型肋的腹板上(如前图4所示)。由于粘贴应变片所用的胶水层厚度、钢结构表面抛光度等因素存在差异，试验测得的数据和有限元结果之间有一定的误差。通过对比可得，两者的趋势是一致的，总体认为有限元模型能较好地模拟整个结构的应变情况。

图9 应变Fig.9 Strain

综合图9可得，采用异形剪力键的钢空腹夹层板应变较大的地方位于一、二跨T型上下肋腹板靠近剪力键的位置(3、7、4、8、13、17、14点)，同时异形剪力键的腹板处也测试到了相应较大的应变，说明十字形剪力键的腹板也承担了传力的作用。

3.3 应力

图10为设计荷载作用下的Mises应力云图。从图中可得到应力较大的地方主要集中在1、2跨T型上下肋靠近剪力键的腹板边缘处，剪力键的十字型腹板内部也有应力分布，这与试验过程中采集到的应变通过计算后得到的应力分布规律一致。同时剪力键的下盖板也有应力分布，可得采用异形剪力键的钢空腹夹层板、钢架两跨之间力的传递是通过异形剪力键的腹板和盖板同时进行的。采用传统的方钢管钢空腹夹层板的剪力键节点域中方钢管与上下肋接触的部位会出现比较明显的应力集中现象，而由于方钢管的中空构造，此处为结构最薄弱的部位。此时方钢管的侧壁应力相对很小，而内隔板(即盖板)的应力较大，盖板承担了主要的力的传递任务[21]。而异形剪力键与上下肋接触的部位后面设有腹板，有利于力的传递，相较方钢管固有的中空结构，应力集中现象大为降低。通过剪力键腹板与盖板的协同传力，使得剪力键各部位受力更加合理、均匀。

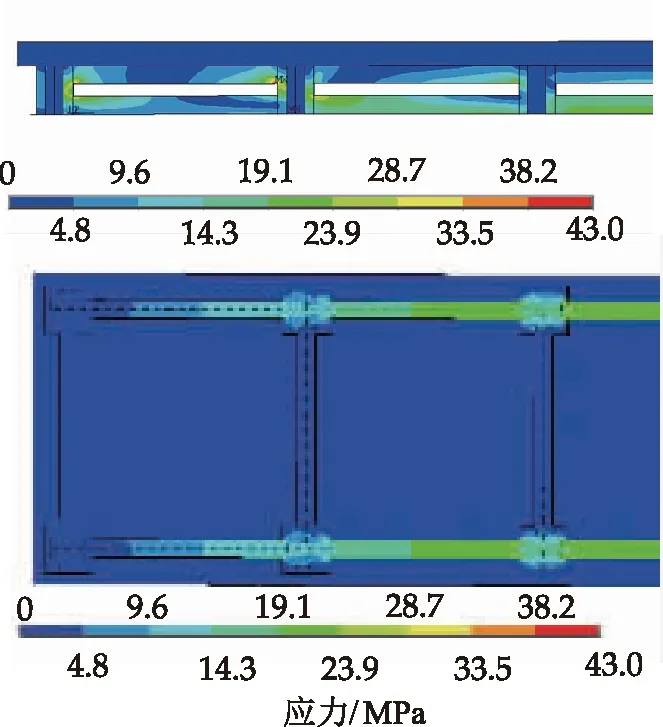
图10 应力云图Fig.10 Stress contour figure

4 结论

对4点支撑5.3 m×1.3 m的采用异型剪力键的钢空腹夹层板进行静力试验和有限元研究，得到以下结论:

(1) 试验中采集的数据与有限元的计算结果相比较，两者挠度的误差小于5%，应变虽有一定误差，但趋势一致。可以认为文中所述的有限元建模方法能较好地反映采用异形剪力键的钢空腹夹层板结构的挠度和应变、应力分布情况。可以在接下来的研究中采用文中所述的有限元的建模方式对不同跨度、荷载及不同截面尺寸的该新型结构继续进行参数化分析和研究。

(2)在加载过程中，混凝土未发现开裂、破坏现象，钢结构上下肋和剪力键均未出现局部屈曲及焊缝开裂的现象。在加载到设计荷载之前，应变和位移有规律地均匀增加，各测定的最大应变未超过所用材料的屈服应变，表明在设计荷载3.0 kN/m2的条件下，整个结构均处于弹性工作阶段。结构的最大相对位移fmax/l=1/2 806<<1/300，结构的最大应力43.0 N/m2<235 N/m2。表明该结构具有较高的整体刚度和较高的安全储备。

(3)与传统方钢管剪力键相较而言，异形剪力键的腹板与盖板的协同传力，使得剪力键各部位受力更加合理、均匀，传力效率更高。