基于模型稀疏表示的单快拍波达方向鲁棒估计
虞 飞,宋 俊,余 赟,庞岩泽
(海军研究院,北京100071)
0 引 言
信号波达方向(Direction of Arrival,DOA)估计作为阵列信号处理中一项极为关键的研究内容,已在无线电通信、雷达、声呐、导航、地震探测等领域有着广泛的应用[1]。在实际环境中,由于多径传播等因素的影响,相干信号是普遍存在的。对于传统的以多重信号分类(Multiple Signal Classification,MUSIC)[2]和旋转不变信号参数估计(Estimation of Signal Parameters via Rotational Invariance Techniques,ESPRIT)[3]算法为代表的子空间类DOA估计算法,由于相干信号源的信号子空间秩个数小于信号源数,导致DOA估计的准确度严重下降甚至估计失败。另外,目标平台(如舰艇、飞机等)在实际工作时经常是快速机动的,特殊情况下需要做复杂而高速的机动动作。这就要求在采样时间内,目标信号需持续入射到阵列,而且入射的信号个数、信号的波达方向不能发生变化。在信号源高速运动、信道快速时变等场合,我们无法进行足够长时间的采样,这时只有少数的快拍可以利用,极端情况下只有一次快拍,此时,基于多快拍数据的DOA估计算法已经无法适用[4-5]。
近年来,基于稀疏表示框架的阵列参数估计方法引起了相关学者的广泛关注,并取得了大量高质量的研究成果[6-11]。这类方法的显著优点是它们在有限采样快拍数据、相干多径信号、阵列模型误差、信号DOA角度间隔小等非理想条件下,都具有很好的鲁棒性。考虑到在实际应用中,目标信号个数远小于传感器阵元数,目标信号DOA相对于空间来说也是稀疏的,本文将传统的传感器阵列输出模型进行稀疏化表示,得到阵列输出数据的稀疏表示模型,研究了一种基于l1-范数最小化的单快拍DOA估计算法(简称L1-min算法)。该算法将稀疏参数求解问题转化为二阶锥规划(Second-Order Cone Programming,SOCP)问题的一般形式,并在二阶锥规划的框架下求解[12],同时探讨了算法中正则化参数的选取依据。L1-min算法在小样本、相干多径信号、目标信号角度间隔小等非理想条件下具有很好的估计性能。
1 阵列输出模型
考虑K个远场窄带信号入射到由M个无方向性(全向)阵元构成的均匀线性阵列(Uniform Linear Array,ULA),并假设K个信号与ULA在同一平面内(在实际应用场景中,如水下声呐基阵测向,我们经常只关心某一平面内信号的入射方位,或者入射信号在该平面内的投影,因此,这一假设可以得到保证)[13]。将阵元由1到M进行编号,并以阵元1作为基准或参考阵元。设参考阵元处的任一接收信号变换到基带后有如下形式[14]:

那么,在t时刻,整个阵列的M×1维输出数据模型为

式中,s(t)=[s1(t)…s(t)]T为变换到基带后的参考K阵元处接收到的K个信号构成的列向量,n(t)=[n1(t),…,nM(t)]T为阵列的零均值加性复高斯白噪声向量,A=[a(θ1)…a(θK)]为M×K维导向矢量矩阵,且对于ULA,导向矢量a(θk)可定义为[15]
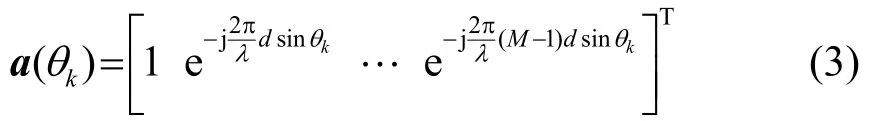
式中,d为相邻阵元间距,λ为信号波长,θk为第k个信号的波达方向(DOA),通常定义为该信号入射方向与ULA法线方向的夹角,则有θk∈[- π/2,π/2]。
2 模型的稀疏表示与稀疏矩阵方程的求解



直接求解优化问题式(5),必须筛选出向量γ(t)中所有可能的非零元素,由于搜索空间过于庞大,故此方法是非确定性多项式时间(Non-deterministic Polynomial-time,NP)困难的。
考虑到l1-范数是最接近于l0-范数的凸目标函数,目前,使用最广泛的求解方法是将l0-范数最小化问题(5)转化为凸松弛的l1-范数最小化问题(简称L1-min算法),即:

首先,将l1-范数最小化问题(6)转化为标准SOCP问题形式。
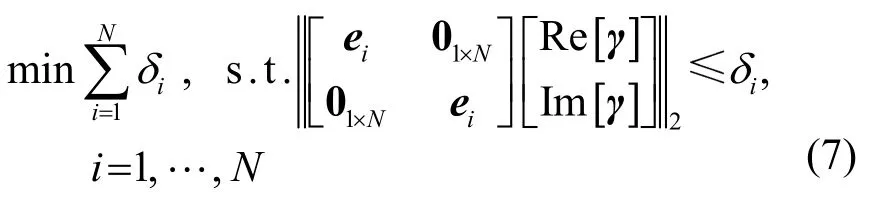
式中,ei为N×N维单位阵I的第i行构成的一个1×N维行向量,Re[·]和Im[·]分别表示取实部和取虚部。
证明:因为


也即
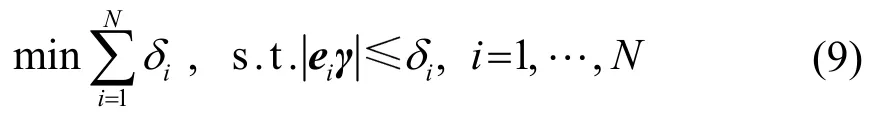
又因为
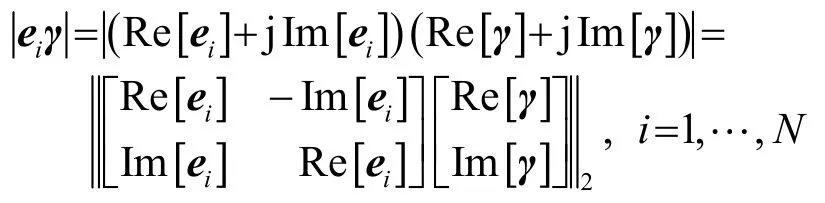
所以,结论(1)得证。
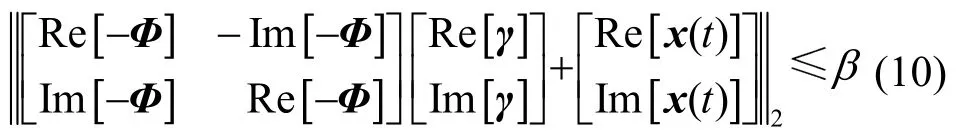
由(1)、(2),则式(6)中的原l1-范数最小化问题转化为如下形式的标准SOCP问题:



3 仿真实验
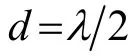
3.1 两个独立信号情形
考虑两个独立信号分别以DOA参数θ1=-10°,θ2=60°入射到上述均匀线阵,图1给出了基于L1-min算法和常规波束形成算法(Conventional Beamforming,CBF)得到的归一化空间功率谱图。图2给出了两个独立信号分别以DOA参数θ1=-10°,θ2=-5°入射到上述均匀线阵时,基于以上两种算法得出的归一化空间功率谱图。
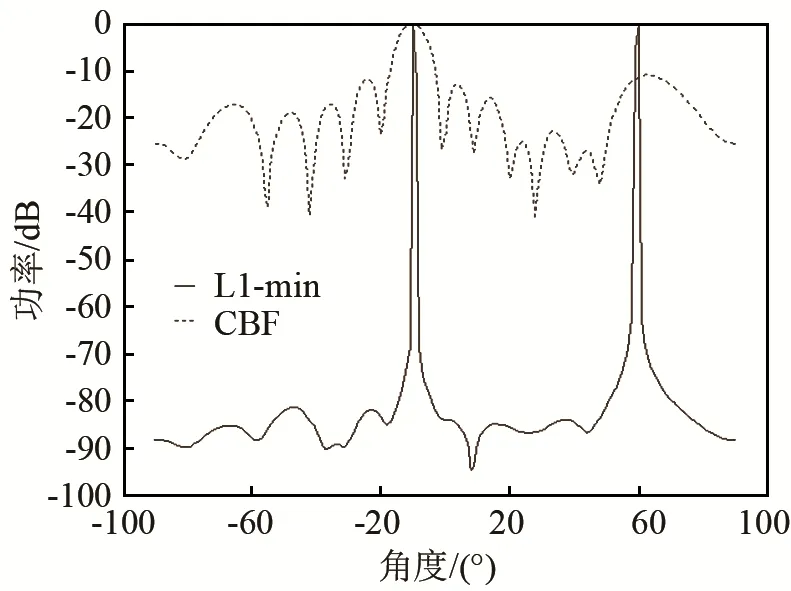
图1 角度间隔较大的两个独立信号DOA估计的归一化空间功率谱Fig.1 Normalized spatial power spectrum for DOA estimation of two independent signals with large angular spacing
由图1的仿真曲线可以看出,当目标信号的角度间隔较大时,采用L1-min算法和CBF算法均可以在真实的目标方向上形成谱峰。而且,本文算法的谱峰比CBF算法更加尖锐,更加对准目标真实方向,旁瓣比CBF算法的旁瓣也低得多。由图2的仿真结果可发现,当目标信号的角度间隔较小时,本文提出的 L1-min算法仍能在真实的目标方向上形成尖锐的谱峰。相反,CBF算法在两个真实的目标方向上的谱峰合二为一,说明此时CBF算法无法分辨两个信号的DOA。综合图1和图2可知,对于独立信号的情形,L1-min算法对目标信号DOA估计的精度和分辨率都比CBF算法高。

图2 角度间隔较小的两个独立信号DOA估计的归一化空间功率谱Fig.2 Normalized spatial power spectrum for DOA estimation of two adjacent independent signals
3.2 两个相干信号情形

图3 角度间隔较大的两个相干信号DOA估计的归一化空间功率谱Fig.3 Normalized spatial power spectrum for DOA estimation of two coherent signals with large angular spacing
由图3的仿真曲线可以看出,当相干信号的角度间隔较大时,采用L1-min算法和CBF算法均可以在真实的目标方向上形成谱峰,与图 1相比发现,两个算法的估计精度和分辨率并没有因为信号相干而有显著下降。但本文算法的谱峰比CBF算法更加尖锐,更加对准目标真实方向,旁瓣比CBF算法的旁瓣也低得多,而且CBF算法旁瓣的高度与主瓣高度相差变小。由图4的仿真结果可发现,当相干信号的角度间隔较小时,本文提出的L1-min算法仍在真实的目标方向上形成了尖锐的谱峰。相反,CBF算法在两个真实的目标方向上的谱峰合二为一,说明此时 CBF算法无法辨别两个信号的DOA。综合图3和图4可知,对于相干信号的情形,L1-min算法对目标信号DOA估计的精度和分辨率都比CBF算法高。
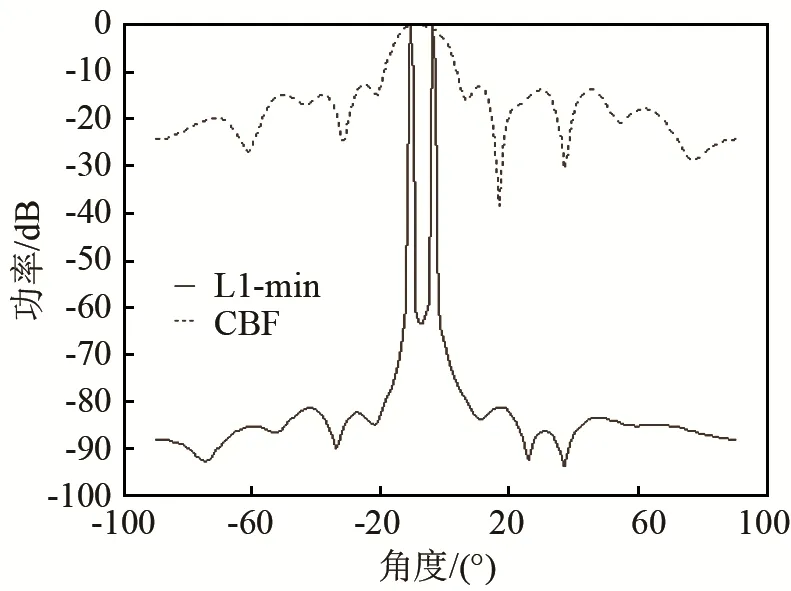
图4 角度间隔较小的两个相干信号DOA估计的归一化空间功率谱Fig.4 Normalized spatial power spectrum for DOA estimation of two adjacent coherent signals
需要说明的是,本仿真实验中的信噪比 SNR为15 dB。在低信噪比情况下,无论目标信号之间是否相关,本文算法仍能在真实的目标角度附近形成明显的尖峰。只是随着信噪比的降低,算法对目标信号DOA的估计精度会有所下降,归一化稀疏功率谱的旁瓣级有所升高,但并不影响本文算法对DOA的整体估计效果。
4 结 论
本文对传统的传感器阵列输出模型进行了稀疏重构,提出了一种凸松弛的l1-范数最小化 DOA估计算法(L1-min),给出了l1-范数最小化优化问题的详细求解方法,分析了算法中正则化参数的选取依据。仿真结果表明,本文算法在单快拍、相干多径信号、目标信号空间间隔很小等非理想情况下都具有较好的估计精度和分辨率,因而非常适用于快变相干信号DOA的实时跟踪估计。本文同时指出,正则化参数的选取直接关系到最终的稀疏恢复性能,然而在很多情况下,对正则化参数的选择是很困难的,尤其是在对噪声的统计特性一无所知的情况下,这也是L1-min算法的局限性所在。事实上,正则化参数对噪声的统计特性和信噪比十分敏感。因此,研究提出一类无需进行正则化参数选取的稀疏参数估计算法是后续值得研究的问题。

