舰船尾流图像的边缘分割算法研究

任秀艳，陈梦英，许伟杰

(1.中国科学院声学研究所东海研究站，上海201815；2.中国科学院大学，北京100190)

0 引 言

尾流作为一类水下声目标，具有十分重要的军事意义，在海战之中起着重要的作用：(1)尾流能够影响探测设备的正常工作；(2)尾流是鱼雷进行探测、攻击目标的重要物理场；(3)尾流能作为潜艇规避的屏障[1]。因此，对各类舰船尾流的声学特性，包括尾流的产生、持续时间和空间的分布、尾流中气泡升浮的速度以及气泡散射与吸收的特征、水下声学尾流成像等方面进行研究日益重要[2]。

既准确又直观的尾流图像可以为下一步的尾流特征研究奠定基础，而在尾流多波束声呐的原始图像中，不仅有尾流回波，还有海面回波反射以及其他噪声干扰，因此需要采取有效的图像分割方法把尾流从中提取出来，从而分析尾流特征。对尾流图像处理时，可把尾流图像看作三维表面，即x、y轴分别为图像的横、纵向矩阵列数，z代表强度的灰度。图像边缘分割已有较长的历史，边缘是图像特性发生变化的位置，不同的图像灰度不同，边界处会有明显的边缘出现，利用这种特征可以进行图像的分割。

1 测量系统及原始数据

多波束声呐测量系统由船载分系统和水下分系统两大部分组成，水下系统的水密舱中包含多波束声呐。课题组于海上进行了多次实验，采用的坐底式多波束测量系统图如图1所示。

图1 测量系统示意图Fig.1 Schematic diagram of the measuring system

原始尾流图像如图2所示。当主瓣收到的尾流信号与旁瓣收到的海面反射信号同时到达时，海面反射信号会干扰尾流信号。

图2 原始尾流图像Fig.2 Original wake image

图2中，海平面在高度约为30 m的中间亮条处，海平面上方的虚拟强度图像由多波束旁瓣引起，在此不做讨论。根据分析，亮环即为海面回波反射干扰，中间条状区域即为尾流图像区域。尾流图像边缘提取的目的是将亮环剔除，并将条状区域的尾流边缘提取出来。

2 尾流图像去干扰处理

利用传统的滤波方法难以去除声呐尾流图像中海面反射强度干扰，因此本文用背景相减法来去除海面回波干扰，构造了一个包含“亮环”噪声并且没有尾流图像的背景环境，通过声呐图像与构造的“亮环图像”相减得到的尾流图像如图3所示。

以图3为原始图像进行尾流图像边缘分割，下面分别介绍几种边缘分割算法，并给出这几种边缘分割算法提取到的尾流边缘。

图3 背景相减法滤波结果Fig.3 Results of background subtraction filtering

3 尾流图像边缘处理

3.1 Canny算子对尾流边缘的提取

基于一阶的边缘检测算子中，Canny算子是公认的具有良好检测性能的一类边缘检测算子，因此本文利用它对尾流图像进行边缘提取。

首先，用高斯滤波器对尾流图像进行平滑处理。然后，利用普通的一阶边缘检测算子，如Sobel算子、Roberts算子等进行梯度计算，本文中选用的Sobel算子。再利用非极大值抑制的方法判定边缘梯度值，在尾流检测的过程中，进行的非极大值抑制是在梯度方向上的非极大值抑制，实际处理的尾流图像的像素点是离散的二维矩阵，对于某个监测点，梯度方向两侧的点不一定存在于二维矩阵中，本文通过插值来解决这个问题。将某点梯度幅值与插值作比较，若此处梯度幅值大于两个插值，则此点就是局部极大值，为尾流边缘点。最后，进行阈值设置、拼接边缘，具体思路是选取两个阈值，认为小于低阈值的点是弱边缘，大于高阈值的点是强边缘，介于中间的像素点需要进一步检查[3]。

边缘检测过程中尾流图像阈值的设置很关键，也是难点，合适的阈值既要尽量保存尾流边缘信息也要抑制噪声，避免引入错误边缘。Matlab自带的Canny算子就是通过直方图来设定阈值的。它默认选择直方图中幅值大小排在前 70%的最后一个阈值为高阈值，低阈值为高阈值的 0.2倍。本文在利用Canny算子处理实验数据时借鉴了此方法，先将所有梯度值进行排序，经过多次测试，高阈值从高到低开始试验，保证噪声逐渐增大，因为阈值设定越高，噪声抑制效果越好。最终选择排在整个梯度值序列中第 98% 处的幅值作为高阈值，低阈值约为高阈值的0.2倍。这里设定的阈值是经过多次实验后选取的。图4、5为利用低阈值和高阈值检测到的弱、强边缘。

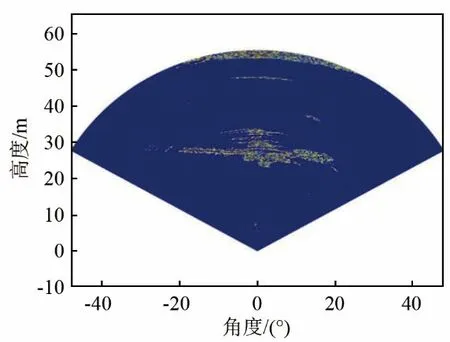
图4 Canny算子弱边缘检测结果Fig.4 Weak edge detection result by using Canny operator

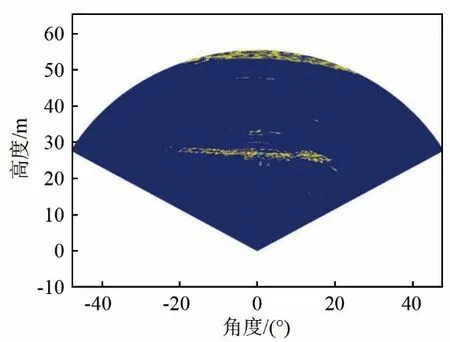
图5 Canny 算子强边缘检测结果Fig.5 Strong edge detection result by using Canny operator

最后以高阈值提取的强边缘作为“种子”，在低阈值提取的弱边缘中寻找其 8连通域，作为Canny算子检测的最终边缘[4]。Canny算子检测的尾流最终边缘如图6所示。

需要说明的是，设定的高阈值不需要检测出所有的尾流边缘，只需要在弱边缘的基础上有分布，之后会利用强、弱边缘，进一步判断、连接尾流边缘。从图6中可以看出，Canny算子处理得到的尾流边缘图像噪声较小。

图6 Canny 算子最终的边缘检测结果Fig.6 Final edge detection result by using Canny operator

3.2 Laplace算子对尾流边缘的提取

拉普拉斯(Laplace)算子采用的是二阶差分计算，在数字图像中(如尾流图像)，对于一阶微分图，认为极大值或者极小值点，是边缘点；对于二阶微分图，认为极大值和极小值间过零的点是边缘点[5]。

Laplace算子在点(x,y)处的定义为

用差分方程近似二阶偏导，结果如下：

提取系数后得Laplace算子模板为

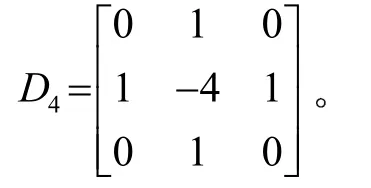
Laplace算子二阶差分的性质对噪声会有双倍加强，所以在进行尾流边缘提取时，将高斯滤波与算子结合起来使用。Laplace算子模板即卷积核，因为尾流图像是二维图像，需要在两个方向求导，直接使用Laplace算子即可自动完成，而上文中使用Sobel一阶算子时需要分两个方向计算。将卷积核与尾流图像进行卷积运算，当Laplace算子检测出过零点时，判定有尾流边缘存在，但不包括无意义的过零点，因为当二阶导数为0时，不仅仅是在尾流边缘，也有可能在独立的噪声点上。利用Laplace算子检测尾流边缘的结果如图7所示。

在图像处理中，边缘检测是重要的一步。尤其是在尾流测量中不仅要求较好地检测到边缘，还要求边缘尽可能连续。在图7中，利用Laplace算子检测尾流图像边缘时可以检测到较为全面的尾流边缘信息，但是同时也有更多的噪声。由于噪声的影响，有些特征的边界不清晰。同样，经典的边缘检测算子由于引入了各种形式的微分运算，对噪声非常敏感，且不能得到较好的结果，不利于后续工作，因此Laplace并不是理想的检测尾流的算法。

图7 拉普拉斯算子的边缘检测结果Fig.7 Edge detection result by using Laplace operator

3.3 数学形态学对尾流边缘的提取

利用Matlab软件对尾流图像进行形态学处理，可以把图像中的尾流边缘分割出来。腐蚀过程注重物体的边界点，可以消除或者弱化边界点，通过腐蚀操作可以对不同区域进行分割并且可以消除目标结构元素的点。与前文介绍过的微分算子相似，在形态学算法中，结构元素也能用模板形象定义。矩形模板中，1表示属于结构元素，0表示不属于结构元素。遍历原尾流图像中的每一个像素点，将其与模板的原点(原点需要自己定义，在本文中定义中心点为原点)对齐，若模板中心为1的位置在原图像上都有对应的像素，则保留模板所在位置的像素点，然后取模板中所有1覆盖下、原图中对应像素中最小值，用这个最小值替换当前像素值。

相同图像利用不同结构元素进行腐蚀操作的结果不同，因此结构元素的形状和大小决定了腐蚀操作的性能。图8给出了本文模板和它对应的结构元素形状。

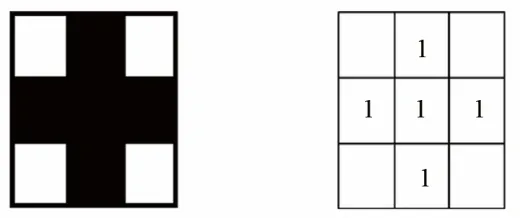
图8 图像腐蚀模板Fig.8 Image corrosion template

膨胀操作与腐蚀操作相对。在遍历图像的像素点的过程中，保留模板所在位置的像素点，然后取模板中所有 1覆盖下、原图中对应像素中的最大值，用这个最大值替换当前像素值。腐蚀操作使目标图像收缩，膨胀操作使目标图像扩展。利用收缩或扩展后的图像可以精确地提取原图像的内外边界。这样提取的边界理论上更精确，也能有效控制边界线条的宽度[6]。

先对图像进行腐蚀操作然后再进行膨胀操作的运算称为开启运算。对尾流图像进行开启运算后结果如图9所示。

从图9中可以看出，与尾流原始图相比，尾流背景中的某些数据元素被消除，集中体现在-30°和30°附近，主要因为这些数据点的回波强度相对较弱。在图9中也发现，尾流图像内部出现了一个个闭合的小圈，形态学处理算法会把相似的邻近的物体连接起来，这在某些图像处理中有非常好的效果，但在尾流图像处理中我们需要的是尾流的外边界，至于尾流内部回波强度的大小，只需要大致范围即可，并不需要细致的归类。要想得到尾流完整的外边界还需要对图 9中的声呐尾流数据设置阈值，进一步提取边界，这就增加了算法的复杂性。

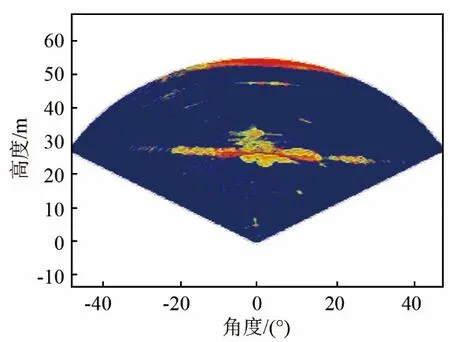
图9 先腐蚀再膨胀的边缘检测结果Fig.9 Edge detection results of first corrosion and then expansion

先对图像进行膨胀操作然后再进行腐蚀操作的运算称为闭合运算。对图像进行闭合运算后，尾流图像进行闭运算结果如图10所示。

由图10可以看出，利用闭合算法可以把尾流边缘大致勾勒出来，但是尾流区域内部也出现了更小的封闭边缘。闭合算法与开启算法相比，尾流元素丢失更多，在开角 -20°和20°附近也丢失了很多数据。

图10 先膨胀再腐蚀的边缘检测结果Fig.10 Edge detection results of first expansion and then corrosion

3.4 分形算法对尾流边缘的提取

分形维数一般都是通过线性拟合的方法计算。最常用的分形维数计算方法是盒计数分形算法，在对尾流边缘提取的过程中，采用的是差分盒计数分形算法，其他的计算方法大部分都是基于盒计数的基础上[7]。下面介绍差分盒计数分形算法的原理和实现过程。

盒计数分形维数通过式(4)计算：

其中：Nr为盒子个数；r为盒子大小，通常取r=1,2,4··2i。

把图像放置在平面上，构成的灰度曲面如图11所示，然后把图 11中的平面用网格进行划分，然后用不同大小的盒子去覆盖图像的灰度平面。计算覆盖整个灰度曲面所需的盒子的个数，上述过程的示意图11所示。

图11 差分盒子算法示意图Fig.11 Schematic diagram of differential box algorithm

对于不同的r可得到不同的Nr：

式中：nr(i,j)为小盒子尺度r下的像素点(i,j)处的小盒子数量。Nr这是尺度为r时覆盖整幅图像的盒子数，变换尺度又得到另一组数据。采用最小二乘法拟合得到的各组点(l og2r,log2Nr)，并在双对数坐标系中标出，通过对这些分布点进行最小二乘线性拟合，直线的斜率取绝对值后即为盒维数[8]。

但采用盒维数计算尾流图像的分形维数时，首先需将图像中所关心的尾流区域提取出来，先转化为黑白位图，在相应矩阵是由 1、0表示，离散的像素点很容易判断网格是否覆盖了图像中的尾流区域。统计出相应网格中覆盖尾流区域的网格数目，拟合8个点为例，即在8个尺度下，得出的尾流图像维数为1.77，误差e为1.5%，结果如图12所示。

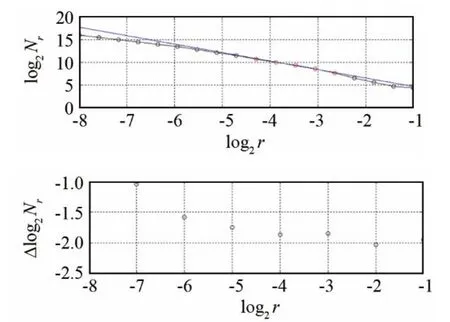
图12 最小二乘法拟合的盒维数图(维数为1.77，误差为1.5%)Fig.12 Box dimension diagram of least squares fitting(Dimension is 1.77,Error is 1.5%)

图12显示了 lo g2(Nr)与log2r的典型关系。拟合误差e值越低，说明拟合误差越小，拟合效果越好。可以根据维数d的数值变化和波动确定图像的边缘并作为分割标准来分割图像。通过设置阈值，如果d在阈值内则判定此区域为尾流内部，若超出阈值则判定为边界。本文为了提取出尾流边缘，经过多次试验将d的范围设定为1.7～1.9。

拟合 18个点得到的尾流图像维数为 1.85，误差e为3%，如图13所示。

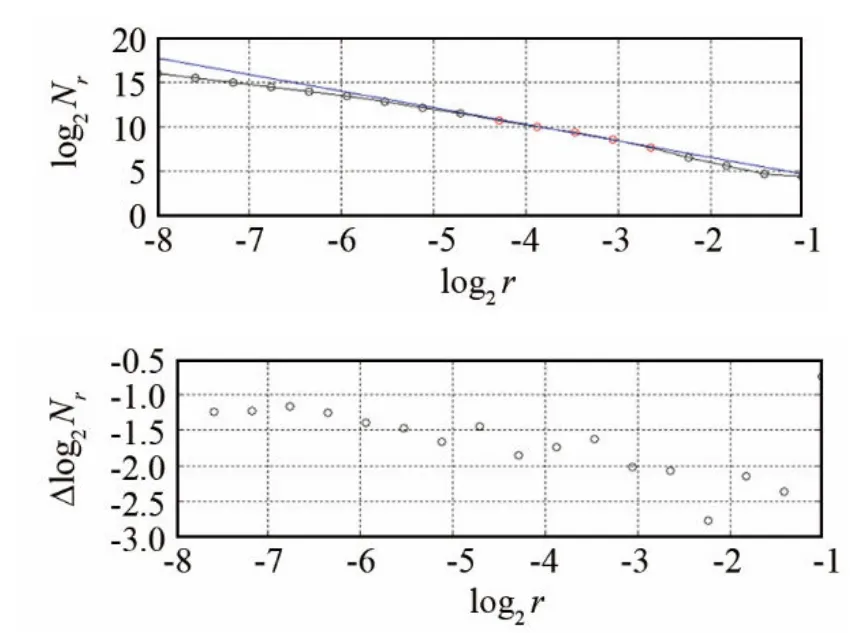
图13 最小二乘法拟合的盒维数图(维数为1.85，误差为3%)Fig.13 Box dimension diagram of least squares fitting(Dimension is 1.85,Error is 3%)

当输入图像(图像必须为二值化图像或者是灰度图像)时，函数的返回值为一个与输入图像大小一致的二值化图像。函数会根据设置的尾流维数阈值检测输入图像的边缘，检测到边缘的图像位置数值为1，其余部分用0填充。这样在读取尾流图像时，分形算法会对图像边缘做处理，勾出尾流的边界。经分形处理后的效果图如图14所示。

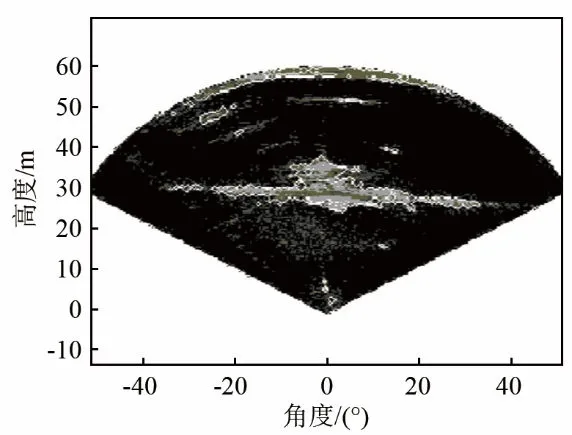
图14 分形算法边缘检测结果Fig.14 Edge detection results of fractal algorithm

由图 14中可以清晰地看到尾流图像的上下边缘，尾流边缘被分割出来。在计算盒子的过程中，随着小盒子大小的变化，盒子数量会发生变化，导致维数d也会变化，对不同图像的影响程度也不一样，在尾流图像中需要对不同大小的盒子尺度进行计算从而得到维数范围，使用计算简单的盒维数可以快速求出图像的分形维数。与传统的经典图像边界算法相比，分形盒计数算法能够忽略纹理内部的变化情况，能够很好地提取尾流图像的边缘轮廓，这为下一步尾流特性的研究奠定了基础。该算法适应于维数变化明显的边缘提取过程，但是盒维数不能很好地反映出图像中的具体变化情况，其值仅由图像块中灰度的最大值和最小值决定。

4 结 论

通过几种边缘检测算法对尾流图像处理的结果进行分析，得到以下结论：(1)Canny微分算子在算法实现过程中首先进行高斯滤波，然后使用一阶微分算子计算梯度幅值与方向，经过非极大值抑制后，通过双阈值判定、连接尾流边缘，低阈值检测的边缘可以提取丰富的尾流信号信息，高阈值检测的边缘噪声较小，不足之处是算法较为复杂过程繁琐，也会出现边缘不连续的情况，从尾流图像的处理结果来看是较为理想的边缘提取算法。(2)Laplace微分检测算子在对尾流图像边缘提取的时候可以检测到尾流的边缘信息，但鉴于此种算法基于的是二阶导数的原理，一阶导数的局部峰值会造成Laplace算子判定为过零点，容易被噪声影响，所以理论上不适用于尾流图像处理。(3)数学形态学算法不像微分算法那样对噪声敏感，同时也能提取到光滑直观的尾流图像边缘，抑制了小的离散点或者尖峰，也能够连接邻近的物体图像填充细小空洞，但这也造成了在尾流图像内部出现了不同程度的闭合区域，出现过分割的现象。(4)分形算法利用不同物体具有不同的分形维数这一原则，通过判断维数奇异值来判断尾流图像与周围区域的分界处，从而提取到尾流边缘，不牵扯到微分计算过程，对噪声敏感性弱，但该算法更适应于维数变化明显的边缘提取过程，随着分割精度的增加，要求的迭代次数也大大增加，造成运行时间比其他算法长。