凸概率密度分布簇下的多损失鲁棒优化等价模型及在直营连锁企业中的应用
徐蕾艳
(南京信息职业技术学院 数字商务学院,江苏 南京 210023)
0 引言

在鲁棒优化理论方面,常见的是两种情形,一种是不涉及不确定变量下扰动集合下的鲁棒优化,另一种是随机变量扰动下的鲁棒优化,后一种是鲁棒随机优化,一般是在一个概率分布簇下或者是围绕一个概率分布扰动情形下的鲁棒优化。
早期的研究主要是扰动集合或概率分布簇下的鲁棒优化研究模型的求解方法,例如,Soyster[2]用线性优化模型来构建解决不确定的问题模型,得出所有属于一个凸集的数据都有可行的解。Ben-Taj、Nemirovski[3]和Ghaoui[4]对于不确定的半定规划和二次规划鲁棒优化方法做了一定的研究,对于鲁棒优化理论的建立与发展做出了一定的而贡献。Popescu[5]、Delage[6]研究了均值和协方差矩阵扰动分布的凸优化鲁棒模型方法。Natarajan[7]和Zymler[8]研究了最坏情形风险价值下的鲁棒模型求解方法。
鲁棒随机优化模型在金融里也有许多研究,一般是研究一种混合概率分布簇的情形,它是有限分布函数的凸组合,例如,例如Huang和Zhu[9,10]针对证券组合投资问题提出了一种WCVaR模型,WCVaR是定义在一个混合分布簇上的最坏情形下CVaR值,他们证明了WCVaR在混合分布下等价一个线性规划问题求解,对于证券组合投资比CVaR反映更有效。Takeda和Kanamori[11]同样证明了鲁棒CVaR问题等价于一个有限多个分布簇的优化问题,用于统计学习里。

综上所述,研究各种分布扰动情形下鲁棒随机优化,对于解决实际问题具有重要的理论意义和实际价值。本文将提出一种凸概率分布簇下鲁棒优化模型,可以用来解决直营连锁企业的产品分配供应管理问题。直营连锁公司(direct chain enterprise,简称DCE),是由公司总部直接经营、投资、管理它的连锁零售店的经营,特别是对它的连锁零售店的商品销售进行定价、分配与供应等方面实施统一管理。一直以来,直营连锁企业的生产分配供应问题一直都是需要解决的重要问题,在服装和食品企业尤为明显,生产供应过剩或不足现象尤为普遍,如何提供最优的生产与分配供应策略已成为影响连锁企业生存亟待解决的重要问题。然而,针对直营连锁企业研究最多的是在营销、物流等方面[19~23],这些研究表明了连锁经营策略的有效性,但是,针对直营连锁企业在生产分配供应方面的理论与应用研究却很少,有必要对连锁企业的生产分配供应策略进行研究。为此,为了解决连锁企业的生产分配供应问题,已经研究了在生产总量与基于期望损失下的单周期最优生产分配供应模型[24],导出了最优分配供应策略下的连锁企业的最佳生产分配供应策略。但由于未来产品概率需求分布存在波动,这种波动可以通过一种概率分布簇描述,使得我们找出概率分布簇下的最坏情形下的生产分配供应鲁棒策略,规避未来需求风险波动导致的损失。故本文建立了一种凸概率分布簇下的单周期生产分配供应鲁棒模型,用于解决直营连锁企业的产品生产分配供应问题。
1 凸概率密度分布簇下的单周期期望均值鲁棒优化模型
本节首先导出凸概率(密度)分布簇下的一般单周期期望鲁棒模型的等价模型。凸概率分布簇是一类具有广泛意义的分布簇,例如文献[9~11]中涉及的概率分布簇就是一类凸概率分布簇。
设ϑ={pτ(ξτ)(τ∈Γ)}是由各种因素产生的概率密度函数分布簇,其中ξτ是一个连续型随机变量,对应的概率密度函数分布pτ(ξτ)(τ∈Γ)ξτ∈[0,+∞),概率分布函数为Pτ(ξτ),假设Pτ(ξτ)=0,当ξτ∈(-∞,0];Pτ(+∞)=1,其中Γ⊂RN中是一个非空凸集合。
定义1如果τ1,τ2∈Γ对应的密度函数分布为pτ1(·),pτ2(·)∈ϑ,对任意的t∈[0,1]有tτ1+(1-t)τ2∈Γ,使得tτ1+(1-t)τ2对应的密度函数为:
ptτ1+(1-t)τ2(g)=tpτ1(g)+(1-t)pτ2(g)∈ϑ
称ϑ是一个关于参数集合Γ的凸概率密度分布簇,对应的{Pτ(ξτ)}构成凸概率分布簇,其中Pτ(ξτ)的概率密度分布函数是pτ(ξτ)。
凸概率密度分布簇总是存在的,文献[9~11,17]是凸概率密度分布簇。下面是2个凸分布簇的例子。
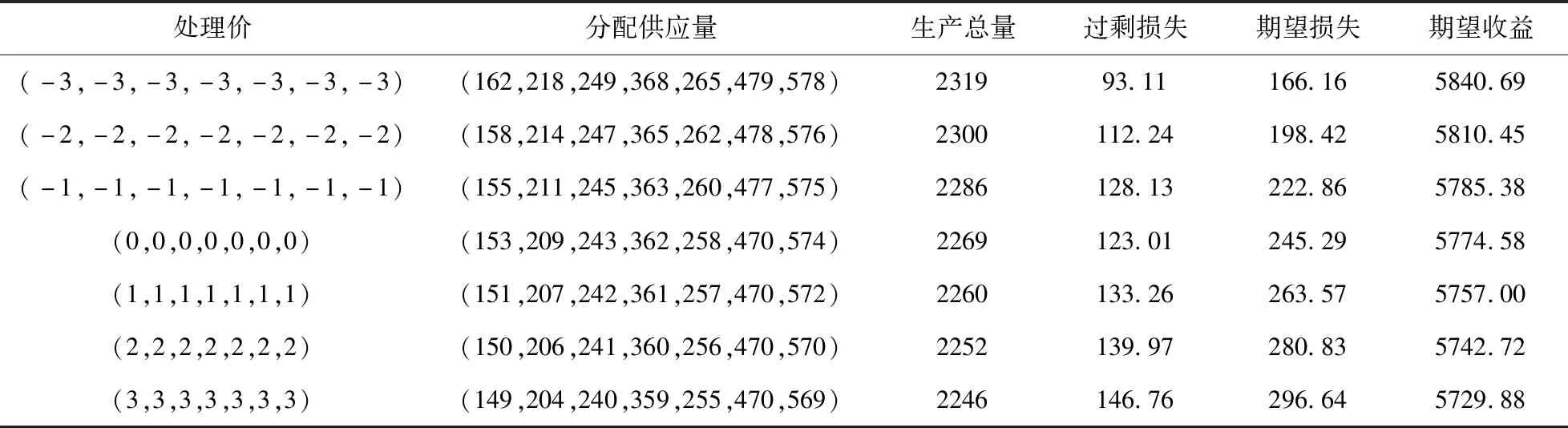
例1设给定1个均匀分布簇:ϑ={pτ(ξτ)|τ∈Γ=[-ε,ε],ε>0},其中给定0<ε 其中τ是扰动变量, 不同τ的随机变量ξτ(τ∈Γ)变化范围不同,这是一个同分布簇,Γ=[-ε,ε],显然ϑ是一个凸概率密度函数分布簇。 例2[9,10]:在实际问题中,已知N个分布密度函数:pk(ξ),k=1,2,…,N, 做凸组合集合: 设g(x,ξτ):Rn×R1→R1是关于决策变量x在随机变量ξτ影响下的损失函数,X是决策集合,ξτ是一个关于凸参数集合Γ下的凸概率密度分布簇的随机变量,对应的概率密度函数分布pτ(ξτ)(τ∈Γ),ξτ∈[0,+∞)。定义在概率密度分布簇ϑ上的最小最大期望均值单周期鲁棒模型为: 定理1设X是一个凸集合,g(x,ξτ)是关于x的凸函数,ϑ是一个关于凸集合Γ的凸概率密度分布簇,则: (1) 定理2设X是一个凸集合,g(x,ξτ)是关于x的凸函数,ϑ是一个关于凸集合的凸概率密度分布簇,则:(1)(P1.1)问题等价于求解下面鲁棒模型: s.t.Eg(x,ξτ)≤u,∀τ∈Γ,x∈X,u∈R1 (2)特别是概率密度分布簇为有限个分布的凸组合(称之为混合概率分布簇): (2) 则模型(P1.2)等价于下面鲁棒模型 k=1,2,…,N,x∈X,u∈R1 ϑ={pτ(ξτ)=(pτ1(ξτ1),pτ2(ξτ2),…,pτm(ξτm))|τ =(τ1,τ2,…,τm)∈Γ=Γ1×Γ2×…×Γm)} 显然,概率密度分布簇ϑ是凸概率密度分布簇。 基于权值w=(w1,w2,…,wm)定义在凸概率密度分布簇ϑ上的单周期最小最大期望多损失鲁棒模型为: 定理3设X是一个凸集合,gi(x,ξτi)(i=1,2,…,m)是关于x的凸函数,ϑ是一个关于凸集合Γ的凸概率密度分布簇,则: (3) 下面我们导出模型(P1.4)的另一个等价模型。 定理4设X是一个凸集合,gi(x,ξτi)(i=1,2,…,m)是关于x的凸函数,ϑ是一个关于凸集合Γ的凸概率密度分布簇,则 (1)(P1.4)问题等价于下面求解下面鲁棒模型: s.t.Egi(x,ξτi)≤ui, ∀τi∈Γ,ui∈R1,i=1,2,…,m (4) ui∈R1,i=1,2,…,m 定理1.4表明鲁棒模型(P1.4)等价于模型(P1.6),下面我们用鲁棒模型(P1.6)来建立直营连锁企业的单周期生产分配供应鲁棒模型。 直营连锁企业中许多产品是单周期重复生产销售的,例如面包直营公司中的各种面包,有的品种一天生产一次,当天销售完,有的品种7天生产一次,7天销售完。直营连锁企业在销售周期中进行生产,当上个周期销售完毕,再直接供应给每个连锁店进行下一个周期销售。因此,大多数产品很容易积累多个销售周期的销售量数据(需求样本)。我们可以通过这些样本获得多个周期的近似概率分布簇。 本文将考虑产品销售需求样本数据可以获得多个周期分布下的近似概率分布簇,如得到N个需求样本周期的概率分布簇{pi(ξi)|i=1,2,…,N},可以计算出对应的每个周期销售需求近似均值和近似方差。我们容易发现,不同产品需求均值和方差在每个周期上具有不同的波动,有的产品还具有较大的波动。对于需求波动变化大的产品,需要利用需求概率分布簇建立新的单周期生产分配供应模型确定相应的生产分配供应策略。即寻找概率分布最大期望损失对应的最小期望损失的单周期生产分配策略。我们建立鲁棒模型的目标是在需求概率分布最坏的情形下找出最好的单周期生产分配供应策略。 假设:(1)连锁公司的所有连锁店个数为有限个,连锁店统一接受连锁公司的相同产品进行销售,所有产品具有相同的有效期和生产期,产品销售按单一周期供应一次,在销售期内销售完不进行补充产品。 (2)一个销售周期分正常价格销售时段和产品处理时段(或打折时段),即产品在正常销售时段按统一零售价格进行销售,在正常销售时段结束时间点进行盘点,每个零售店根据盘点剩余产品的库存量按处理价卖余下的产品,按处理价一定可以处理完所有产品。 (3)已知可以获得所有连锁店的多个销售周期的近似需求概率分布。 (4)总生产量供货能力分最大生产总量和给定生产总量。 (5)已知单位产品零售价,每个连锁店的成本价和处理价。 按上面假设,直营连锁企业对于每一个连锁店会有一个供应损失,受到供应生产总量的限制,直营连锁企业需要决定生产多少商品按一个最优的分配供应给所有的直营连锁店,尽量使得总损失最小。 先给出下面符号假设: a:单位产品零售价。 ci:单位产品成本价为(含运输费、运营费、保管费等),且a>ci。 ei:单位产品在过剩时(处理期)的处理价格,ei>0表明需要花费处理费用(产品没有残值),ei<0表明产品单位残值(在处理期内进行折价销售),ei=0表明剩余未售出产品的价值为0。 xi:分配供应给第i个连锁店的数量,是决策变量。 Q连锁企业的总生产供应量,需要满足:x1+x2+…+xm=Q。 ϑi(i=1,2,…,m)是一个凸概率密度分布簇。 ξτi(τi∈Γi):第i个连锁店的随机需求变量,对应的概率密度分布簇为pi(ξτi)(τi∈Γi),概 率分布函数为Pτi(ξτi),假设Pτi(ξτi)=0,当ξτi∈(-∞,0];Pτi(+∞)=1,其中Γi⊂RN是一个非空集合,对应的均值为μτi。 fi(xi,ξτi):第i个连锁店在分配供应量xi的损失函数。 k=1,2,…,N,i=1,2,…,m xi≥0,ui≥0,i=1,2,…,m 如果给定生产总量Q, 采用(P1.6)建立单周期鲁棒模型: k=1,2,…,N,i=1,2,…,m x1+x2+…+xm=Q xi≥0,ui≥0,i=1,2,…,m k=1,2,…,N,i=1,2,…,m ui≥0,i=1,2,…,m k=1,2,…,N,i=1,2,…,m x1+x2+…+xm=Q,x∈X ui≥0,i=1,2,…,m 下面列举几种实际中存在的分配约束集合。 (1)连锁店分配界约束 设si,Si(i=1,2,…,m)分别是第i个连锁店最小和最大分配供应量限制,那么得到分配约束集合X={(x1,x2,…,xm)|0 (2)区域最大生产总量有界约束 … xi≥0,i=1,2,…,m} (3)给定区域生产总量有界约束 当直营连锁企业区域将m个连锁店划分成t个区域,每个区域有m1,m2-m1,…,m-mt-1个连锁店,直营企业给第i个区域给定供应量为Qi(i=1,2,…,t),那么得到约束集合 X={(x1,x2,…,xm)|x1+x2+…+xm1=Q1 xm1+1+xm1+2+…+xm2=Q2 … xmt-1+1+xmt-1+2+…+xm=Qt xi≥0,i=1,2,…,m} 另外,我们还有一些生产分配供应约束情形,例如生产资源约束、物流线路分配约束和有限资金分配约束等,这里不进一步的考虑。 下面提出上面三种生产分配供应鲁棒模型的线性规划近似求解方法。 (5) 其中(k=1,2,…,N,i=1,2,…,m)。设wi第i个连锁店的损失权重,wi>0,给定初始值:N,a,ei,ci,wi(i=1,2,…,m)。 下面给出上节三种模型的线性规划模型。 单周期期望均值鲁棒模型(P2.1)可以转化求解下面的线性规划鲁棒模型: k=1,2,…,N,i=1,2,…,m xi≥0,ui≥0,i=1,2,…,m 模型(P2.2)可以转化求解下面的线性规划鲁棒模型: k=1,2,…,N,i=1,2,…,m k=1,2,…,N,i=1,2,…,m,j=1,2,…,J x1+x2+…+xm=Q,xi≥0, ui≥0,i=1,2,…,m 鲁棒模型(P2.3)可以转化求解下面的线性规划鲁棒模型: k=1,2,…,N,i=1,2,…,m k=1,2,…,N,i=1,2,…,m,j=1,2,…,J x∈x,ui≥0,i=1,2,…,m 其中X是分配限制约束。鲁棒模型(P2.4)可以转化求解下面的线性规划鲁棒模型: k=1,2,…,N,i=1,2,…,m k=1,2,…,N,i=1,2,…,m,j=1,2,…,J x1+x2+… +xm=Q, x∈X,ui≥0,i=1,2,…,m (6) 容易利用Matlab软件中线性规划函数直接求解,得到(P3.1)~(P3.4)的最优生产分配供应策略。后面的案例分析仅针对上述鲁棒模型进行数值分析。 我们选取了直营食品连锁企业生产供应同一种产品历史数据,进行了计算获得近似的4个周期正态概率分布,分别给出了7家连锁店的4个周期的近似概率分布(构成混合概率分布簇)对应的均值和方差。设连锁店个数m=7, 零售价a=10元, 成本价c=[5,5.5,6,5.2,5.3,5.2,5.7]元,该产品有效周期为七天。处理价仍然取7个进行生产分配供应策略比较,下面分析处理价、需求方差变化、 给定不同生产总量和分配权值变化等情形下鲁棒模型(P3.1)和(P3.2)的生产分配供应策略比较。本文的数值实验目标主要包括如下几个方面:当处理价格变化时,分析期望鲁棒模型(P3.1)生产分配供应策略的总供应量、分配量、期望损失和期望收益损失变化;分析期望鲁棒模型(P3.1)最优生产分配供应策略与偏离最优生产分配供应策略的对比;分析需求波动与方差波动对最优生产分配供应策略的影响;分析了给定生产总量下期望鲁棒模型(P3.2)生产分配供应策略的变化;分析给定生产总量下期望鲁棒模型(P3.2)目标权值变化对近似最优策略的影响等问题。 本文中所有计算结果都是由MATLAB软件编程实现,下面是部分数值实验结果与分析。 表1 不同处理价下最大生产量为4000时的生产分配供应策略比较 (2)我们分析了模型(P3.1)和模型(P3.2)在需求变化的最优生产分配供应策略趋势,数值结果表明,当在原需求基础上增加时,期望损失、期望收益和生产总量都逐渐增大,说明当需求减小时,这三个量随着相应的减小,表明生产分配供应策略随着需求变化而变化,需求变化会带来供应损失。需求变化引起鲁棒模型的最优生产分配供应策略对应变化,随着需求增大,生产总量增大。随着处理价增大,生产总量减小,以达到规避需求变动时引起的供应过剩或不足风险的目的。特别是需求方差增大时,若采用最优生产分配供应鲁棒策略时,应采取对应处理价的生产总量进行生产分配供应,减少生产总量,规避波动变大时产生的供应过剩或不足损失。 (3)我们分析了模型(P3.1)和模型(P3.2)给定生产总量控制下的最优生产分配策略变化,数值结果表明在给定生产总量的情形下,当生产总量偏离最小风险损失的最佳生产量时,期望风险损失增大,期望收益减小。但是,最优生产总量的期望最小风险损失对应的期望收益不一定是最大的,也就是说,若模型(P3.1)的求得最优生产总量时,适当减小供应量时,尽管增加一定的期望风险损失,期望收益有可能增加。因此,企业把生产分配总量控制在损失最小的生产总量与利润最大的生产总量之间,保证尽可能多的获得利润。 例如,当需求方差增加100时,处理价为0时,模型(P3.1)得到的最优生产量为2173,最小损失403.27,期望收益为5528.57。图4.1给出处理价为0时给定订购总量[2120,2220]的期望损失和期望收益的变化趋势,当生产总量为2151时,计算得到的损失风险403.36,期望收益为5550.75为最大(见图1)。若采用偏离分散供应的生产总量2151得到的生产分配供应策略的期望收益为最大。因为从图1看到,当订购量在2140到2210时,风险损失几乎不变,即最大期望收益损失点的损失值403.39接近最小期望损失点损失值403.27,而对应的期望收益在2151时到达最大值5550.75,在2173时附近期望损失最小点对应的期望收益几乎达到最小值5529.58。 总之,通过鲁棒模型(P3.1)和(P3.2)可以确定一个对应的处理价下的订购总量区间,得到对应的期望最大利润与期望最小损失的生产总量。需求波动大时取区间中小的订购总量对应的最优生产分配供应策略,需求波动小的时候建议取区间中大的订购总量对应的最优生产分配供应策略。 图1 处理价为0时给定订购总量对应的期望总损失和期望收益变化趋势 (5) 给出了区域生产分配约束的期望鲁棒模型比较 对于分配约束的期望鲁棒模型(P3.3)和(P3.4)可采用线性规划模型进行求解。在这个案例中7个连锁店,前4个在同一个区域(它们之间实际距离比较近些),后3个连锁店在同一个区域(它们之间实际距离比较近些)。由于受到下一周期的资金产生的控制,换算成分配量后,第1个区域至少供应900,最多供应1000,第2个区域至少供应1100,最多供应1200。得到区域约束条件为:X={(x1,x2,…,x7)|900≤x1+x2+x3+x4≤1000,1100≤x5+x6+x7≤1200}。 表2是模型(P3.3)获得的不同处理价生产分配量、生产总量、风险损失和期望收益结果。表2中当处理价增大时生产总量及分配量逐渐减小,风险损失增大,期望收益减小。表2中生产总量低于(P3.3)的生产总量,风险损失变得更大。表3是模型(P3.4)获得的不同处理价生产分配量、生产总量、风险损失和期望收益结果。表3中当处理价增大时生产总量及分配量逐渐减小,风险损失增大,期望收益减小。与表2的结果相比较,在处理价小于0时表3的结果与表1的生产分配供应策略不同。这里看到分配约束不同,得到的最优生产策略不同。表2与表3的生产分配策略存在较大的差异。 表2 分配约束下模型(P3.3)的分配供应量、生产总量、风险损失和期望收益 表3 分配约束下模型(P3.4)的生产分配量、生产总量、风险损失和期望收益 本文首先提出了基于参数集合的凸概率分布簇概率,建立了在凸概率分布簇下的单周期期望均值鲁棒模型,证明了期望均值鲁棒模型等价于一个较容易求解的数学规划模型。然后,分别建立了直营连锁企业给定最大生产总量、给定生产总量和分配供应约束情形下的单周期生产分配供应期望均值鲁棒模型,在给定多个有限样本周期获得的概率分布下,生产分配供应鲁棒模型可以转化为一个线性规划模型。最后,选择了某直营连锁企业的一个产品的4个周期近似概率分布(构成的混合概率分布簇),针对单周期生产分配供应线性规划鲁棒模型,进行了数值实验,结果表明了单周期期望均值鲁棒模型可以提供期望损失最小或期望收益最大的近似最优生产分配供应策略,期望均值鲁棒模型比期望均值模型获得更加保守的生产分配供应策略。当需求波动大的产品,随着处理价的增大,生产总量和分配量对会相应减少,规避需求波动过大时产生的风险损失。 另外,我们还给出了分配约束的单周期生产分配供应期望均值鲁棒模型,如分配变量界约束鲁棒模型、区域最大生产总量与区域给定生产总量约束的生产分配供应鲁棒模型。这些鲁棒模型可以转换为线性规划模型求解,容易求得相应的单周期生产分配供应鲁棒策略,为直营连锁企业提供生产分配供应决策指导。






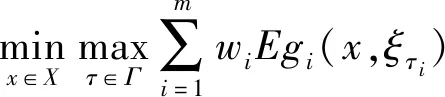



2 单周期生产分配供应期望均值鲁棒模型





2.1 最大生产总量限制单周期鲁棒模型

2.2 定生产总量限制鲁棒模型

2.3 带有分配约束限制的单周期生产分配供应鲁棒模型




3 单周期生产分配供应鲁棒策略近似计算方法


3.1 最大生产总量限制线性规划鲁棒模型

3.2 给定生产总量线性规划鲁棒模型

3.3 带有分配约束限制线性规划鲁棒模型




4 数值分析






5 结论

