运用思维导图 优化数学教学
谢宏宇
【摘 要】思维导图图文并茂、结构分明,是一种有效的思维工具。在数学教学中运用思维导图,可以帮助学生掌握新知识要点,构建知识网络,高效复习知识,整理易错题型,是学生学习与成长的“锦囊”与“阶梯”。本文在解读思维导图基本概念、分析思维导图教学应用价值的基础上,着重探讨思维导图在数学教学中的有效应用策略,以期能发挥思维导图的教学辅助作用,让思维之花在数学课堂绽放异彩。
【关键词】数学教学;思维导图;教学效率
瑞士教育家裴斯泰洛齐说:“教学的主要任务不是积累知识,而是发展思维。”发展学生的思维是数学课堂教学的灵魂所在。而思维导图的教学方式,可以借助图文并茂的特色,应用于学习、记忆、整理、复习等思维阵地,发挥其教学辅助作用,帮助学生更好地理解和掌握数学知识,培养数学思维品质。下面,本文结合具体实例,就思维导图在数学教学中的有效应用展开探讨,以期能为广大数学教师提供一些有价值的借鉴。
一、思维导图基本概念解读
思维导图,又称心智导图,其核心思想是综合、有效利用人的发散性、联想性思维,以图文并茂的形式促进人高效地思考与记忆,是一种革命性的思维工具。在绘制思维导图时,首先应找到关键的中心词汇,如核心知识点。其次,列出与中心词汇相关联的知识点为核心的分支,按重要程度依次排列。再次,将各分支联系在一起,利用不同的颜色、形状展示知识内在结构。最后,标注图中各知识点关系,构造简单清晰的知识结构,以增强学生的理解力与记忆力。
二、思维导图教学应用价值分析
在数学教学中,合理运用思维导图教学,能对学生左、右脑同时进行刺激,将复杂的、枯燥的数学知识利用直观形象的图形转化为简单易懂、容易记忆的逻辑框架。这样的教学以培养学生的学习兴趣为基础,以发展发散思维能力为出发点,使原本看似散乱的知识点在学生头脑中形成一幅全景图,让学生明确知识结构,掌握知识要点。
三、思维导图在数学教学中的应用途径
(一)借助思维导图,高效复习知识点
复习课不同于新课教学,涉及知识点较多,需要学生对知识加以巩固与衔接,是一种系统概括性学习。教师通过建立知识网络结构图,可以帮助学生在学习中理清思路,将复杂的知识简化,提升学生对知识的理解和学习效果。
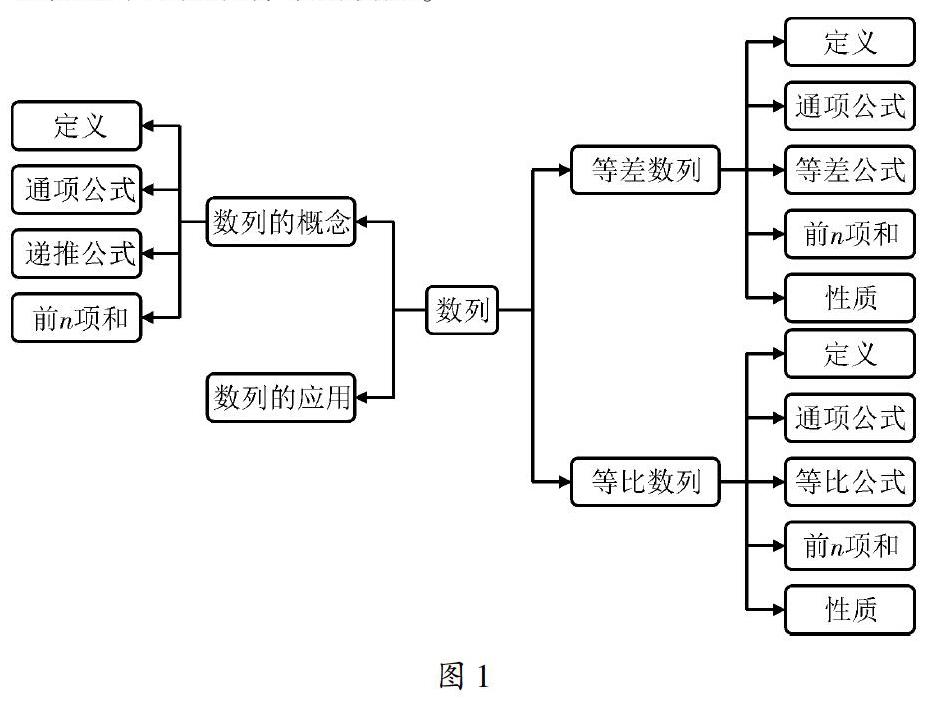
例如,在复习“数列”这一部分的内容时,为了让学生更加全面、系统地掌握知识点,教师可以借助思维导图梳理数列的相关内容,如图1。教师可以将“数列”作为中心词汇,逐渐辐射出“数列的概念”“数列的应用”“等差数列”“等比数列”等二级节点。然后再从二级节点逐步梳理出三级、四级节点,如二级节点“数列的概念”可以辐射出“定义”“通项公式”“递推公式”“前n项的和”这四项三级节点,而二级节点“等差数列”则可以辐射出“定义”“通项公式”“等差中项”“前n项和”“性质”等三级节点。这不仅能细化相关知识点,使学生能更为全面地了解这一章节的所有大小知识点,也能帮助学生提升逻辑思维水平,把握知识点之间的关系,提升复习效果。
数学知识具有较强的逻辑性,针对一个知识点可以辐射、发散出一串知识点,形成系统的知识体系。而思维导图的思维发散特点正好可以展现、综合这些知识点,思维导图的绘制可以促进学生知识体系的构建。
(二)引入思维导图,掌握新知识要点
教师可以根据学生的实际情况,选择学生可以自学的难度较低的新课内容,先让学生进行小组内讨论,根据教师布置的学习任务进行自主学习,再让学生根据自己的理解绘制思维导图,归纳知识点,在学习小组内进行展示、交流与沟通,通过“自学—议论—引导”的模式,完善学生的思维导图,让其更好地掌握新知。
例如,在教学“集合与集合间的关系”这一综合性较强的内容时,教师可以先带领学生简单复习“个体与集合的关系”知识点,随后逐渐导入新的集合关系知识点。个体与集合的关系分为“属于”和“不属于”两种,通过判断个体是不是集合中的一个元素,即可判断两者间的关系。基于对这一点的认识,学生可以通过思维导图进行思维发散,即通过判断集合中的所有元素是不是完全属于另一个集合来判断该集合是否包含于另一个集合。之后,教师再趁热打铁继续追问:“仅关注一个集合便足够了吗?”答案是否定的,从而过渡到对另一个集合的考查,帮助学生清晰且深入地理解“相等集”“真子集”的概念。
教师在新知识的引入过程中可以进行思维导图的展示,构造简单清晰的知识结构,理清其中元素与集合、集合与集合间的逻辑关系,利用思维导图的学习优势帮助学生更好地理解、记忆新知识,提高课堂教学效率。
例如,《直线与圆的位置关系》这一部分内容中,直线与圆的基本关系包括三种:相交、相切、相离。教师可让学生以“直线与圆的位置关系”为中心词语,找出判断方法这一点重点,接着列出相离、相切、相交这三种位置关系,绘制思维导图,从而对应知识点,精准判断直线与圆的位置关系,全面掌握知识内容,提高学生的解题效率。
(三)利用思维导图,整理错题
在学习过程中,学生因为数学概念不清、方法错误、过程不规范、粗心等原因造成解题的种种错误。教师在分析错误原因的基础上将这些错题进行整理、归类,可以使学生在整理错题的过程中得到启发,避免错误再次发生。利用思维导图进行错题整理,围绕一个关键词通过辐射线连接与此相关的所有项目,这样的错题整理融入思考和空间性想象,真正变“错”为宝。
例如,学生可以围绕“不等式错题分析”这一中心词,罗列出含参数的不等式、线性规划中的不等式问题、基本不等式三个二级节点,再根据每个节点“诊断”出相应的三级节点:概念不清、缺乏数形结合意识、对充分不必要条件理解不清、忽视隐含条件、对已知条件不能综合考虑等。教师要引导学生主动归类错题,把错题制作成思维导图,并在每个三级节点处注明具体的错题,分析错解原因及正确的解答,这样,在以后的复习中便能一目了然,更具针对性,从而达到事半功倍的效果。
整理数学错题集是一个良好的学习习惯。教师应指导学生挑选典型的、有代表性的错题,将错误的原因加以标注,这既能培养学生深入学习与反思的积极性,也能帮助学生形成清晰的思路,将无形的问题有形化,在系统性的思考过程中有所收获、有所提升。
总之,思维导图的巧妙应用,能大大提高学生的学习兴趣,让板书更加形象、直观,提高数学教学效率。教师应在教学中积极探索应用结构分明、图文并茂的思维导图,帮助学生抓住学习重点,发展数学思維,深入理解课堂内容,逐步发展学生的核心素养。
参考文献:
[1]吴志丹.协作建构思维导图在数学复习课中的应用探究[J].电化教育研究,2010(07).
[2]崔海东.思维导图在高中数学教学中的应用探究[J].中学教学参考,2019(27).
[3]熊飞.让思维导图为中职数学微课教学添活力[J].好家长,2018(33).
[4]杨永辉.数学课堂教学应用思维导图探研[J].成才之路,2019(16).

