冷鲜鸡货架期微生物预测系统的构建

瞿 洋周昌艳索玉娟张东来韩奕奕丰东升杨晓君李苗云

(1. 上海市农业科学院农产品质量安全与检测技术研究所，上海 201403；2. 上海市农产品质量安全中心，上海 201708；3. 河南农业大学食品科学技术学院，河南 郑州 450002)

货架期是指推荐条件下食品保持理想品质的时间长度[1]。微生物活动是影响肉品货架期的主要因素，微生物学方法是预测货架期的常用方法[2]。利用该方法进行货架期预测时，使用何种微生物参数存在一定的争议。研究认为，测定某种优势腐败菌是一种重要手段[3-5]，其中肠杆菌、假单胞菌和热死环丝菌是引起鸡肉腐败变质的常见微生物[6-8]。与假单胞菌相比，肠杆菌能产生与之相同的引起肉品风味变化的挥发性物质[9]，且在鸡肉产品中含量更高[10]，所以是鸡肉产品低温贮藏时比假单胞菌更重要的腐败菌。热死环丝菌在有氧条件下产生丙酮、双乙酰，无氧条件下产生乳酸、乙醇等挥发性化合物[11]，是无氧及微需氧环境中的优势腐败菌。也有研究[12-15]认为，不同食品中优势腐败菌的种类和数量存在一定差异，不同微生物间的相互作用会影响腐败的进程，以单一菌种作为建模对象预测货架期不具有代表性，建议选择菌落总数为研究对象进行货架期预测。

目前，货架期预测手段主要以数学方法为主，且需通过用户自我计算来获得货架期信息，缺乏直观性。李苗云等[3]描述了假单胞菌在鸡胸肉上的生长，确定了生鲜鸡的货架期；董飒爽等[12]测定了菌落总数，并建立了鸡胸肉产品的货架期。ComBase是能在线预测微生物生长的预测微生物学信息数据库，但仍需人工计算货架期，无法直观展示其货架期信息。因此，研究拟选用肠杆菌、热死环丝菌和菌落总数为微生物参数，建立冷鲜鸡货架期动力学模型，并采用皮尔森相关分析比较上述3个微生物参数与货架期预测准确度的相关性，利用Visual Basic语言编写形成冷鲜鸡货架期微生物预测系统，并对该系统进行实际样品验证，旨在实现计算机后台承担货架期公式计算过程，使不具备微生物预测学背景的用户仅输入初始微生物数量和贮藏时间，即可获得当前冷鲜鸡货架期数值，达到简化预测模型应用的目的。

1 材料与方法

1.1 材料与仪器

1.1.1 材料与试剂

冷鲜鸡：构建模型用，上海圣华食品销售公司；

冷鲜鸡：实际样品验证，市售；

结晶紫中性红胆盐葡萄糖琼脂培养基(VRBGA)、平板计数琼脂培养基(PCA)：广东环凯微生物科技有限公司；

STAA琼脂培养基及添加剂：青岛海博生物技术有限公司；

PBS：生工生物工程(上海)股份有限公司。

1.1.2 仪器与设备

高压灭菌锅：SX-500型，日本Tomy Digital Biology公司；

生物安全柜：1300 SERIES A2型，美国Thermo公司；

恒温培养箱：Medcenter Einrichtungen GmbH型，德国Friocell公司；

恒温振荡培养箱：TQZ-312型，上海精宏实验设备有限公司；

电子天平：AL104型，瑞士Mettler Toledo公司；

漩涡混匀仪：Vortex Genie 2型，美国Scientific Industries公司。

1.2 方法

1.2.1 样品处理 无菌条件下分割冷鲜鸡，取鸡腿跟鸡胸肉于无菌均质袋中，参照文献[3]，分别于5，10，15，20，25 ℃恒温培养箱中贮藏192，120，72，55，31 h，每隔一定时间取出1份样品(1只鸡腿、1份鸡胸肉)。

1.2.2 感官评定 按GB 2707—2016执行，自然光照下，对鸡肉样品的色泽、黏度、气味和弹性等方面进行综合评价。

1.2.3 微生物参数测定 无菌操作剪取鸡腿肉和鸡胸肉样品，混合后取25 g加入225 mL灭菌PBS中均质2 min，取均质液1 mL稀释。按GB 4789.41—2016中的肠杆菌科平板计数法测定冷鲜鸡中的肠杆菌，选用平板计数法在STAA琼脂上测定冷鲜鸡中的热死环丝菌总数，按GB 4789.2—2016测定冷鲜鸡中的菌落总数。每个温度设置3组平行，不同温度下测定终止时间以细菌生长达稳定期为准。

1.2.4 冷鲜鸡货架期的建立

(1) 微生物一级模型的建立：常用的一级模型有修正的Gompertz、Baranyi以及Logistic模型。修正的Gompertz模型是经典模拟，被广泛应用于肉品致病菌以及腐败菌的生长预测[2]。Logistic模型适合在生长环境和影响因素单一时使用，另外，两种模型适用于复杂环境。修正的Gompertz和Baranyi模型均考虑了延滞期的影响，前者适用于低温和适温条件下微生物的生长，后者更适用于变温环境[16-17]。试验采用恒温静态法，用修正的Gompertz方程拟合冷鲜鸡肉在不同温度贮藏时的肠杆菌数、热死环丝菌数及菌落总数，描述不同温度条件下上述3种目标菌的生长动态[18]。修正的Gompertz方程如式(1) 所示。

(1)

式中：

N(t)——t时刻菌落数，CFU/g；

N0——初始菌落数，CFU/g；

Nmax——最大菌落数，CFU/g；

μmax——最大比生长速率，h-1；

λ——生长迟滞期，h。

(2) 微生物二级模型的建立：根据一级模型得到的冷鲜鸡中肠杆菌、热死环丝菌和细菌的最大比生长速率和迟滞期，选取平方根模型拟合其与温度之间的生长关系，表达式如式(2)、(3)所示[19]。

(2)

(3)

式中：

μmax——最大比生长速率，h-1；

λ——生长迟滞期，h；

T——生长温度，℃；

Tmin——最低生长温度，℃；

a、b——模型参数。

(3) 冷鲜鸡货架期的建立：通过初始菌落数(N0)到最小腐败量(Nt)所需要的增殖时间来进行预测。按式(4)计算货架期。

(4)

(4) 模型的验证：采用判定系数R2和均方根误差(RMSE)评价一级模型，判定系数R2、偏差因子(Bf)和准确因子(Af)评价二级模型，Bf和Af评价货架期模型[20]，相对误差评价货架期预测系统。R2用来对模型方程的拟合度进行评价，R2越接近1拟合度越高。RMSE可以用来衡量准确度和离散程度。Bf显示了预测值与观测值的偏差程度，Bf<1说明预测值小于观测值，表示该模型处于一个合理的范围。Af显示了预测值与观测值的准确度，Af>1且越接近1，说明预测值和观测值越接近，准确度较高。

(5)

(6)

(7)

式中：

μpre——预测值；

μobs——相同时间下的实测值；

n——试验次数。

(5) 冷鲜鸡货架期微生物预测系统：选用 Visual Basic(VB6 Mini)作为微生物生长预测程序编写工具。

1.3 数据处理

腐败阈值的各指标数据采用Excel 2007进行分析，微生物预测模型数据采用Origin 8.5软件进行拟合，采用Excel 2007软件绘图，微生物参数与货架期准确度的相关性采用Matlab进行分析。

2 结果与分析

2.1 冷鲜鸡腐败阈值的确定

由表1可知，当贮藏温度为5 ℃时，鸡肉在第4天开始出现腐败现象，颜色由淡黄转向橘黄，鲜红转向玫红，且表面发黏，同时伴有异味，肉品整体呈次新鲜状态；此时鸡肉中肠杆菌、热死环丝菌、菌落总数分别为4.433，2.735，5.141 lg(CFU/g)，将其确定为腐败阈值。当菌落数值达到腐败阈值时，会促使微生物产生酶的信号分子，从而加速肉品品质劣变[21]。鸡肉肠杆菌的腐败阈值与郑梦林等[5]的结果接近；菌落总数腐败阈值与高灿灿等[22]的结果相吻合，与董飒爽等[12]的结果相近。

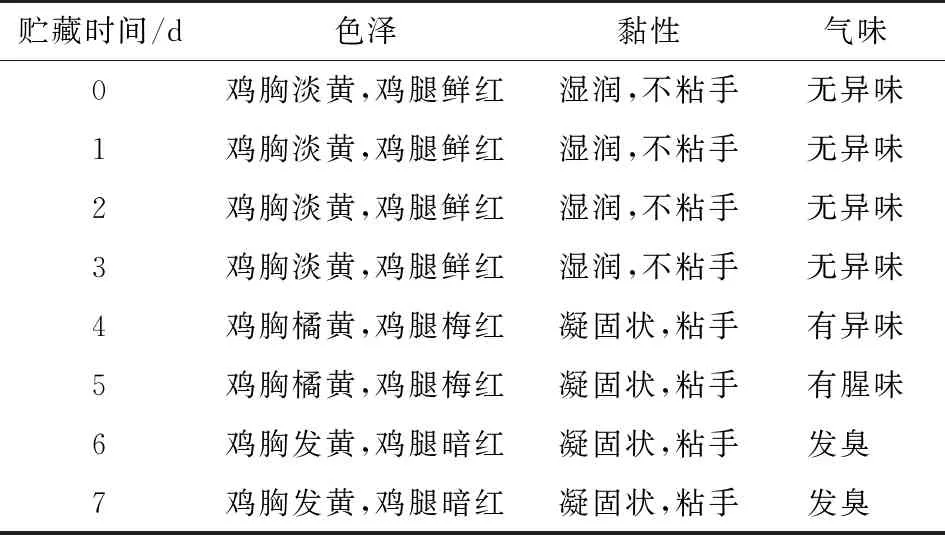
表1 5 ℃时冷鲜鸡的品质变化

2.2 冷鲜鸡货架期模型的建立

2.2.1 冷鲜鸡贮藏期间一级模型的拟合 由图1可知，鸡肉腐败过程中3种微生物参数呈不同的生长状况。由表2可知，R2>0.97，说明修正的Gompertz方程能较好地拟合试验中不同微生物参数的生长情况。随着贮藏温度的升高，微生物参数最大比生长速率升高，迟滞期变短。5 ℃时的最大比生长速率为0.02～0.03 h-1，25 ℃时>0.3 h-1；5 ℃时迟滞期为30～42 h，25 ℃时为4～5 h，说明贮藏温度是影响微生物生长的关键因素，微生物的生长随贮藏温度的不同而发生显著变化，体现了低温贮藏的重要性，与已有研究[23-24]相符。此外，微生物间存在竞争关系，在各自适宜的生长温度下，部分微生物快速生长，另一部分微生物的生长受到抑制。随着贮藏温度的升高，热死环丝菌迟滞期的降幅显著大于肠杆菌(P<0.05)，但其生长速率的增长程度小于肠杆菌。

2.2.2 冷鲜鸡贮藏期间二级模型的拟合 由表3可知，贮藏温度、生长速率及迟滞期的R2>0.94，呈良好的线性关系。根据Ross对偏差因子的划分标准，若Bf为0.90～1.05，越靠近1.00，模型越可靠；若Bf为0.70～0.90或1.05～1.15，该模型也可以被接受[25]。肠杆菌、菌落总数及热死环丝菌μmax的Bf均为0.94～1.06，λ的Bf为1.08～1.13，模型偏差度小。Af值应>1，越靠近1其准确度越高；Braun等[26]认为Af值为1.1～1.9时，模型均可接受。肠杆菌、热死环丝菌及菌落总数Af为1.04～1.33，说明模型准确度高。

2.2.3 冷鲜鸡货架期模型的建立 由表4可知，肠杆菌、热死环丝菌和菌落总数货架期公式的Bf值为0.941 63～0.985 84，与李苗云等[3]建立的生鲜鸡肉货架期Bf值(0.999 99～1.000 52)相比，其偏差范围较大，但属于Ross偏差因子划分标准的模型可靠类别；Af值为1.076 01～1.144 63，小于李苗云等[3]的结果(1.229 34～1.320 56)，说明其准确度更高，属于Braun的可接受范围，故试验冷鲜鸡货架期模型可靠。

图1 冷鲜鸡中微生物的一级模型

2.2.4 微生物参数与货架期准确度之间的相关性 由表5 可知，肠杆菌、热死环丝菌和菌落总数的预测值与货架期的相关系数分别为0.992 3(P<0.01)，0.992 7(P<0.01)，0.995 1(P<0.01)，即肠杆菌、热死环丝菌和菌落总数均与冷鲜鸡腐败相关，均可用于冷鲜鸡货架期的预测。

表2 冷鲜鸡中微生物一级模型生长参数及模型验证

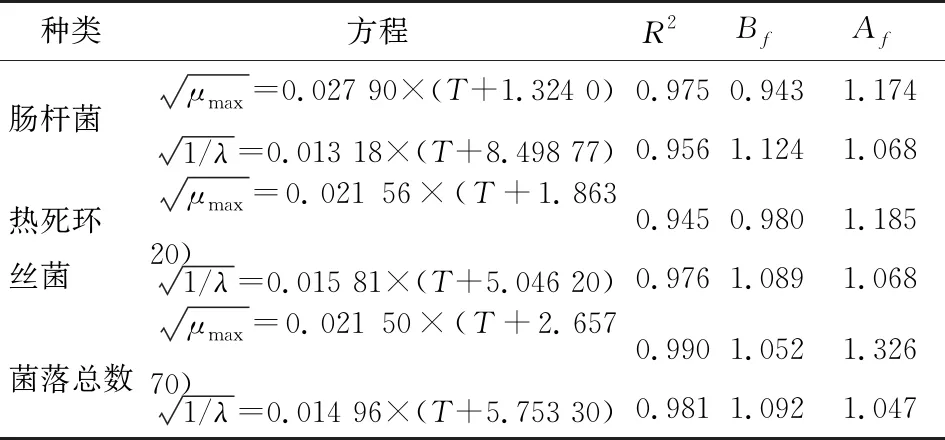
表3 平方根二级模型的评价

表4 冷鲜鸡货架期公式及其评价

其中，菌落总数的相关性最高，热死环丝菌、肠杆菌的次之，说明如果要单一地使用某种微生物参数进行货架期的预测，选用菌落总数会使计算结果更准确。

2.3 冷鲜鸡货架期微生物预测系统的建立及验证

选用 Visual Basic 作为冷鲜鸡货架期微生物预测系统的编写语言，设定软件基本界面(图2)和算法后，使用者在无需了解预测微生物模型的情况下，输入相应的微生物参数便可获得冷鲜鸡货架期，该软件程序已获得计算机软件著作权，登记号为2020SR0107443。

在奉贤区随机采取8份市售冷鲜鸡，2 h内带回实验室无菌操作下将冷鲜鸡分成两份，一份用于初始菌落计数，另一份冷鲜鸡放入4 ℃冰箱冷藏，用于感官评定，若冷鲜鸡市售时未包装，则不测定热死环丝菌的初始菌落数(该状态下引起冷鲜鸡腐败的主要因素为好氧腐败菌)。由表6可知，预测系统的相对误差在9%以内，低于现有文献[3,12]的最大相对误差(10%～21%)，其结果更准确可靠。

表5 微生物参数与货架期的皮尔森相关分析†

3 结论

试验测定了冷鲜鸡贮藏过程中肠杆菌、热死环丝菌和细菌总数的变化，利用修正的Gompertz模型进行拟合获得了冷鲜鸡的货架期计算公式，采用皮尔森相关分析比较了微生物参数与货架期准确度的关系，并通过Visual Basic编写冷鲜鸡货架期微生物预测系统。结果表明，货架期计算公式准确度≥0.94；如果以某一种微生物参数进行货架期的预测，可选用菌落总数,其计算误差最小；使用者在输入相应微生物参数的初始菌落数及贮运温度后即可获得冷鲜鸡货架期值，且最大相对误差<9%。后续可开展不同贮藏温度下冷鲜鸡微生物指标与理化指标相关性的研究。

图2 冷鲜鸡货架期微生物预测系统

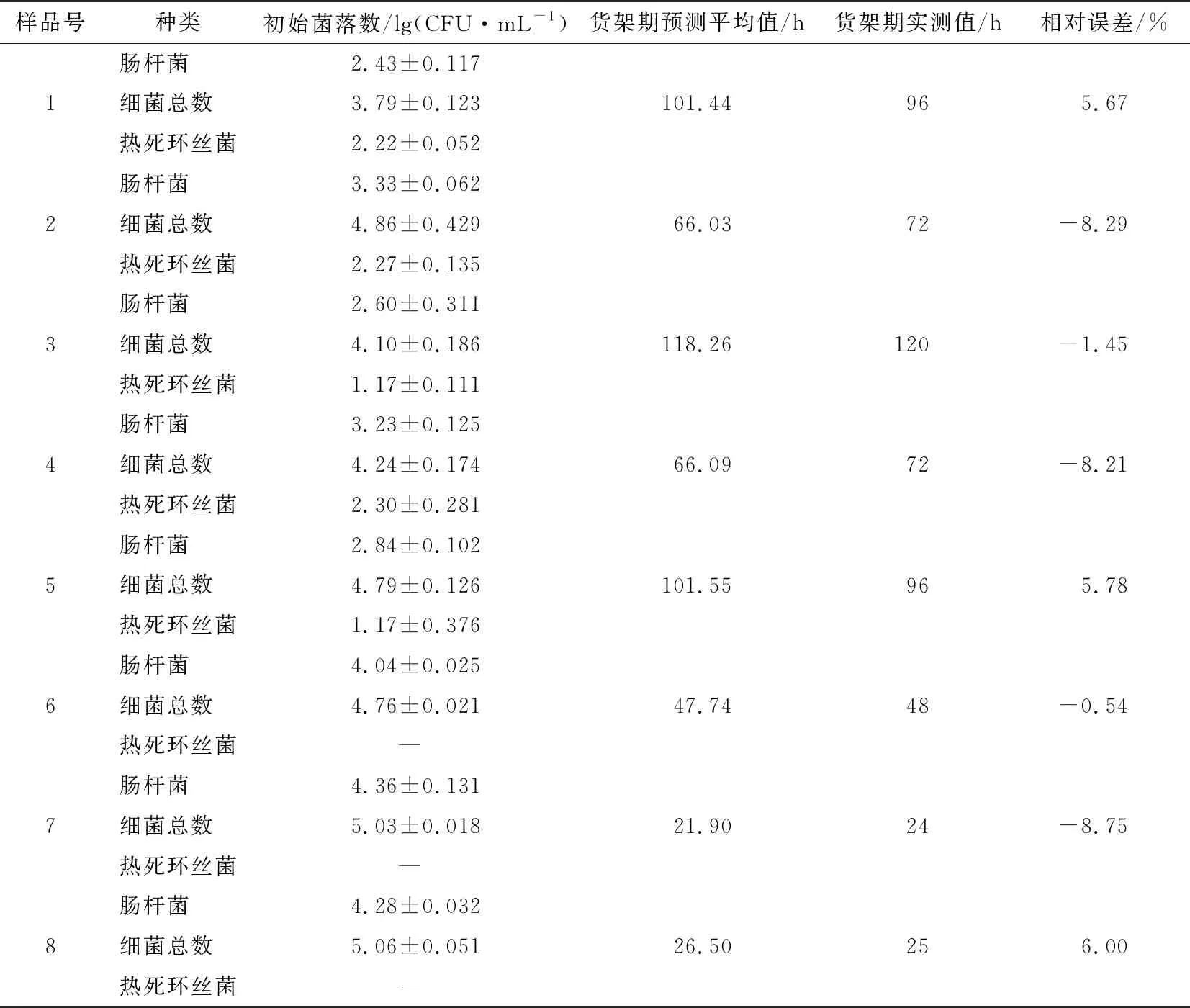
表6 冷鲜鸡货架期微生物预测系统的验证