温故而知新

陆椿

摘  要：数学复习课不仅是为了温故知故，更需达到温故知新。教学中可着眼整体，通过“梳理归类，建立有序的知识结构;题组辨析，把握知识的本质特征;综合运用，激发学生的思维活力;接力创新，促进学习的螺旋上升”等有效策略，帮助学生“复”有所得，“习”有提升。

关键词：数学复习;教学策略

《论语·为政篇第二》有云：“温故而知新，可以为师矣。”意思是：温习旧知识从中得到新的理解与思考，凭借这一点就可以成为老师了。可见，古人对“温故而知新”这一学习方式是非常重视的。审视目前小学数学复习课的课堂教学现状，诸如复习目的性不明、过程系统性不强、习题重复性过多、内容层次性单一等问题均寻常可见。如何才能有效实现复习课“温故而知新”的目的？笔者以为，把握学情，基于系统，通过整体教学策略，不失为一条有效途径。

所谓整体策略，指复习过程中不仅局限于本课的内容和任务，而是注意探寻知识间的前后联系和内在逻辑，着眼整体和系统，从而达到融会贯通，有效提升的一种方式。具体来说，可采用以下几种策略：

一、梳理归类，建立有序的知识结构

复习课，首要是对知识进行梳理。梳理并非新授，不是将知识点重新教一遍，也不是简单地将知识点重现。梳理的重点应是帮助学生形成有序、充满“活力”的知识结构，形成知识体系。学生经过一个阶段的学习，存储积累了不少知识，但是受年龄特征的限制，他们还不具备自主梳理的能力，因此这些知识在孩子头脑中是零碎的、单一的和片面的，处于“无序”的状态。在实际应用知识的过程中，学生就很容易出现似懂非懂和不能融会贯通的情况。数学知识的运用和创新是在有序、高效的知识体系基础上实现的。因此，复习课关键是要帮助学生进行系统梳理和归类，揭示知识之间的内在联系，将分散的知识点连成线、结成网、组成块。

例如，苏教版小学数学五年级下册第一单元“简易方程”的单元复习，知识梳理可以分成这样几个层次：首先是“归类”，引导学生依次整理本单元涉及的主要知识内容—— 一是等式与方程的含义，二是等式的性质，三是用方程解决实际问题。其次是“再现”，结合例子，梳理每个内容所包含的具体知识点，比如等式和方程的具体含义、等式性质的具体表述等。再次是“联系”，在上述基础上引导学生梳理各知识点之间的联系和逻辑关系，如等式和方程的关系，等式性质的具体应用（解方程），用方程解决实际问题的基本步骤，等等。最后是“序化”，沟通与本单元内容相关的知识，如用方程解决实际问题与普通算术方法解决问题的异同等，形成完整的单元知识体系，以思维导图简要示意如下（如图1）。

通过分类梳理，学生对“简易方程”单元的知识有了比较清晰的认识，进一步明确了各知识点之间的联系，在头脑中形成模块化的体系。“有序”的知识，让思维更充满活力。

二、题组辨析，把握知识的本质特征

从整体角度出发，复习时经常需要把新知和旧知进行联系和对比，题组即是常用的训练方式之一。题组以其沟通相近知识联系、突出相异知识对比的特性，能有效促进学生对数学知识和方法本质的理解。

例如，在数的运算的复习中，出示如下题组：

①345+2955=3300;

②18.6+7.88=26.48;

上述是由整数、小数和分数三个计算组成的题组。首先，学生在计算得到正确结果方面显然不存在困难。其次，引导学生通过这三个题目，分别复习整数、小数、分数加（减）法的计算法则，这三种运算表面看来有比较大的差异：整数加（减）法则要求相同数位对齐;小数加（减）法则要求做到小数点对齐;分数加（减）法则强调分数单位要统一。继续引导学生从表面走向深入：实质上三个计算法则的核心都是相同计数单位方可直接相加减，异分母分数之所以不能直接相加减是因为它们的分数单位不统一，需要转异为同。通过题组，让学生不僅进一步理解了上述计算法则，而且将整数、小数、分数加（减）法的计算法则合并，突出本质，更有利于知识的理解和保持。

再如，一般的分数、百分数应用题的复习，笔者设计如下题组：六年级1班有男生25人，女生20人。①男生人数是女生的几倍？②女生人数是男生的几分之几？③男生人数占全班人数的几分之几？④男生比女生多百分之几？⑤女生比男生少百分之几？为了帮助学生更好地理解标准量、比较量和分率三者之间的关系，通过表格来进一步梳理对比：

运用问题题组，引导学生弄清楚解答这类题的关键是先要判断“哪个数量是哪个数量的几分之几、百分之几，还是几倍”“标准量和比较量分别是多少”，由此为解决更复杂的分数、百分数的实际问题积累经验。

三、综合思考，激发学生的思维活力

教材对复习单元的内容一般按纵向的知识体系编排。教师在教学中，就可以多关注知识间的横向联系，让知识点纵横交叉发生关联，综合运用，从而激发学生的思维活力。

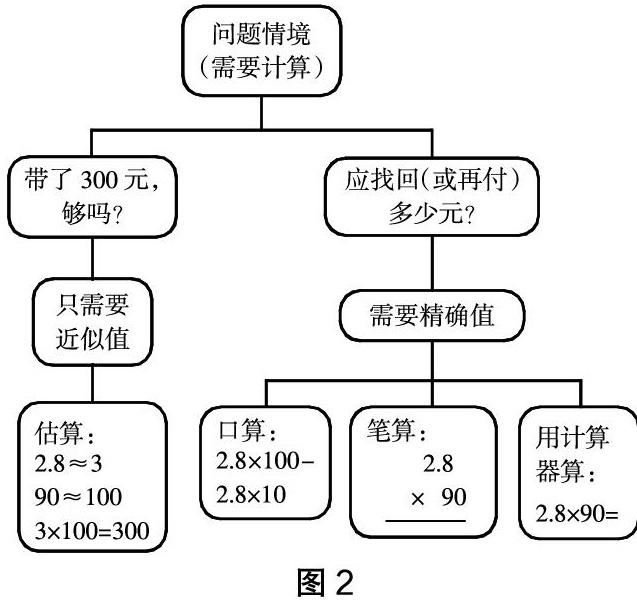
例如，以往我们总是用“口算”“估算”“笔算”“递等计算”“用计算器算”等指导用语单一地指定计算方式，学生很少有多元开放的思考和选择，运算策略方面的培育更是少之又少。因此，复习阶段应有意识弥补这方面的不足。如“老师买90根跳绳，每根2.8元。她带了300元钱，够吗？如果不够，应找回（或再付）多少元？”引导学生综合分析（如图2），沟通几种计算之间的联系。

小学阶段可供选择的计算方式不外乎“口算”“笔算”“估算”“用计算器算”等。我们在日常生活中面临计算的实际问题时，一般先考虑是只需要大致的结果，还是需要精确的结果。如果只需要大致的结果，那么就选择“估算”;如果需要精确的结果，那么还要根据实际情况，选择“口算”“笔算”或者“用计算器算”。

如“妈妈要买一台微波炉和一台电饭煲。微波炉是548元/台，电饭煲是374元/台”。

①购买前思考，带1000元够不够？

②购物满800元可参加抽奖活动，能否抽奖？

③付款时思考，大约要付几百元？

④收银员收款，一共需要多少元？

前面三个问题都只需“估算”，且分别选用“进一法”“去尾法”“四舍五入法”取近似值即可;最后一个问题则需要精确计算。如此复习多个综合知识点，让学生根据现实情境选择计算方法，有利于激发学生的思维活力。

四、接力创新，促进学习的螺旋上升

所谓“接力创新”，是指将已有的思维结晶作为继续超越的起点，向未知的领域开拓创新，如同田径运动中的接力赛一样，后来的人接过前人的“接力棒”继续向前冲刺。复习也是如此，复习题的设计尤其要有层次性，既要达到巩固应用之目的，又要帮助学生在思维能力上有所提升。如六年级总复习“用绳子捆扎瓶子的问题”，设计如下练习层次：

①将两个底面直径为6厘米的瓶子捆扎在一起，需要多长的绳子？（接头处绳长不计）

②将3个瓶子捆扎在一起，需要多长的绳子？如果是4个、5个、6个……各需要多长的绳子？（如图3）

③通过上面的练习，你有什么发现吗？

绳子的长度=（    ）+（    ）。

首先是基础层次，引导学生观察得出：求绳长就是由2个半圆（一个整圆）和2条直径组成的图形周长，即（12+6π）。相信对于大多数六年级的孩子来说，这个问题并不难解决。其次是拓展，由捆扎2个瓶子拓展到3个及多个瓶子，瓶子的个数不同，捆扎的方式及结果也各不相同，依次求得绳子的长度分别为（18+6π）、（24+12π）、（30+15π）、（36+18π）……第三層次，引导学生观察思考瓶子个数、捆扎方法和绳子长度三者之间的联系，发现每增加一个瓶子，绳长就增加一条直径与半个圆周长之和。因此，绳子的长度=直径×瓶子的个数+圆周长的一半×瓶子个数，即C=dn+3πn（n=瓶子个数）。

学生从求捆扎两个瓶子的绳长出发，其实质相当于求运动场的周长，这在平时经常会练习到;在此基础上拓展，最后思考发现“用绳子捆扎瓶子”的特征，循序渐进，通过逐层的思维接力实现学习的螺旋上升。学生在已有的知识基础上，通过复习，汲取新的经验，感悟新的想法，整合新的思路，使思维实现跨度和跳跃。

总之，复习的最终目的不仅是知识的巩固，更是为了帮助学生在巩固知识的过程中继续发展，继续创新。“温故而知新”“温故而创新”，应是我们在数学复习中努力达成的目标。