初探数学教学中 自主合作学习的实施策略

张明建

[摘  要] 自主合作学习是通过明确分工实现教师引导、同伴互助、自主探索的教学模式，鼓励学生为个人和集体利益完成共同任务. 文章以初中数学教学为例，提炼出自主合作学习实施的基本策略：创设富有意义的问题情境;因地制宜地调控教学过程;培养学生勤于思考的习惯.

[关键词] 自主学习;合作学习;数学教学

合作学习指学生在明确责任与分工的基础上，完成共同的学习任务. 自主学习指以学生为主体，通过独立地实践、分析、质疑与探索等方式完成学习任务. 新课标明确提出：要改变课程实施过程中的死记硬背、接受学习等机械的学习现状，倡导以学生的探究、实践为主导的教学方式，培养学生获得新知和处理问题的能力. 而自主合作学习则是结合自主学习与合作学习的优点，响应新课标的教育理念，引导学生在和谐的合作学习环境中，选择恰当的时机，通过自主实践、探索以及与同伴合作交流等方式，分析相应的学习材料，调控学习过程，从而有效地让学生养成善于思考的习惯，以提升学生数学核心素养.

创设富有意义的问题情境

杜威在《民主主义与教育》中提出：“学生所追求的结果与学习情境产生联系，学生就会改变自己的观点，有意识地做出有目的、有意义的行为. ”和谐、民主、自由的學习环境是有效学习的根本，而客观、理性与抽象是数学学科的特性，这也要求数学课堂氛围与其他学科有所差异. 尤其是创设自主合作学习的问题情境时，要综合考虑学生特点和学科特性，引导学生在适度的压力与紧张感中，充分调动合作学习的积极性，通过独立思考与合作交流，逐渐改变自己的观念与行为，从而全力以赴地参与教学活动.

案例1  “矩形的判定方法”教学

问题：

（1）你们对于矩形有怎样的理解？

（2）李红想做一个矩形，她找到长度相等的两对（两根长的一样长，两根短的一样长）木条，完工后，你有什么办法检验她所做的图形是矩形呢？

（3）根据问题（2），总结判定四边形是矩形有哪些方法？

问题（1）主要是为了唤醒学生对矩形的学习情绪，复习矩形的相关特性，为判定矩形夯实基础，具有承上启下的作用.

问题（2）通过小组合作交流的方式，鼓励学生通过案例，思考、交流矩形的判定方法，借助生活实际引出数学问题，既体现出数学的“生活味”，又体现出生活的“数学味”. 学生通过观察、分析与推理，用数学知识揭示生活问题，经历从具体到抽象的思维过程，有效地训练了学生的思考能力、逻辑思维能力以及表达能力.

问题（3）让学生经历“活动——猜想——验证”的过程，此过程均以学生为主体，通过小组成员的思考与分析、合作与交流，让学生亲历知识的发生、发展过程，领悟知识所蕴含的数学思想，经历“形象——表象——抽象”的思维过程.

问题情境活动的展开，离不开和谐、民主、自由的环境，融洽的课堂氛围能满足学生的安全需求，让学生积极思考并勇于阐述自己的看法与观点，良好的对话氛围可将自主合作交流的活动推向高潮. 此教学案例问题情境的创设源自于实际生活，教师以学生合作交流的方式，营造出和谐的教学氛围，引导学生由浅入深地探究、分析问题的来龙去脉，让学生在自主学习与合作交流中，深化对矩形性质及判定定理的理解与掌握.

因地制宜地调控教学过程

教师作为学习的引导者、促进者，要因地制宜地调控教学过程，给予学生合理的评价与指导. 合作学习过程中，难免会出现各种意外，教师应关注学生在合作交流中遇到的障碍与生成的问题，做到及时点拨、适时引导. 尤其是遇到学生回答问题不完整，思路不清晰的情况时，要及时探问、追问，引导学生由浅入深地进行思考，认识问题的本源，从而精准地理解问题，强化对知识点的掌握程度. 对于一些难度大、对思维要求高的问题，可灵活运用一题多解或变式训练等方法，拔高学生思维，使其形成较好的数学思想.

案例2  “等边三角形判定定理”的教学

问题：大家有什么办法画一个等边三角形？

学生经小组合作后展示画法：（1）用尺子画一条线段，用圆规分别以线段的两个端点为圆心，线段长为半径，画两个弧相交，交点即这个等边三角形的另一个顶点.

（2）因为∠A=∠B，所以AC=BC;因为∠B=∠C，所以AB=AC;因为∠A=∠C，所以BC=AB，由此可知此三角形为等边三角形（见图1）.

第一次调控：

师：很好！我们来分析一下，这是根据什么条件来画出的等边三角形？由这种画法，能得出判定一个三角形为等边三角形的方法有哪些？

生：三条边相等是画出等边三角形的基本条件，再根据三角形的两角等于60°来判定此三角形为等边三角形.

师：根据以上的操作与总结，我们能根据两个角为60°的条件画出等边三角形. 请大家再次小组交流并思考，有没有办法用一个角为60°的条件画出等边三角形，请说出理由.？摇

组1：先画∠A=60°，在∠A的两条射线上分别取点B和点C，使得AB=AC. 因为AB=AC，所以∠B=∠C，因为∠A=60°，所以∠B=∠C=60°. 因此，此三角形为等边三角形.

组2：画∠A=60°，在射线边上取任意点C，以C点为圆心，AC为半径画弧与另一条射线相交于点B，可得BC=CA，连接BC，根据条件可知∠B=∠A=60°，故此三角形为等边三角形. 同理可画AB=BC.

第二次调控：

师：我们来分析这两组同学的画法，找找它们之间的相同点，并说说你们的见解.

生：一个角为60°，同时两条边相等的三角形，可以判定为等边三角形.

此案例首先以小组合作学习的方式获得相应的判定定理，再由角和边的性质，启发学生以一个角为60°画等边三角形并展开讨论与思考，探索出新的方法. 两次小组合作将问题逐渐分化，抽丝剥茧地展示了等边三角形的判定方法，整个过程由学生自主合作交流为主，教师引导为辅，条理清晰、节奏合理.

在此教学过程中，教师以等边三角形的画法引导学生根据条件来作图、探索、总结其判定定理. 教师通过对不同画法的调控，鼓励学生自主合作，由浅入深地探究出结论，并通过适时的追问揭示数学本质，学生经历了由具体到抽象，由形象思维向抽象思维的过渡.

培养学生勤于思考的习惯

学生在合作学习中，通过积极参与、主动探索、勇于表达来提升各方面的能力. 合作学习为每个学生的成长提供了良好的空间，让学生在活动中经历探讨、交流，从而发现自身的不足，产生新的理念，获得新的行为. 当然，这一切都以学生的独立思考为前提，学生只有亲历合作与交流过程，开动脑筋，才能形成良好的思考习惯.

案例3  “三角函数”教学

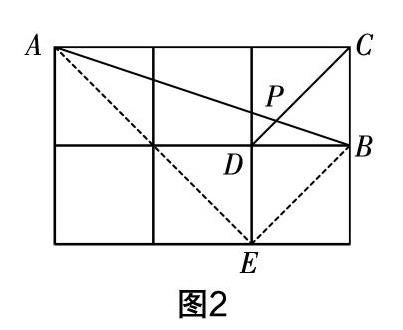
问题：如图2，由同等大小的正方形组成的网格内，点A，B，C，D，分别在小正方形的顶点上，其中AB，CD相交于P点，则tan∠APD的值是多少？

教师可先给几分钟让学生独立思考，之后再组织学生进行小组合作学习，要求各组学生展示解题思路.

组1：过B点作BE∥CD，连接AE，得Rt△AEB（见图2）. 因为∠APD=∠ABE，AE=2BE，所以tan∠APD=2.

组2：过C点作CF⊥AB，F为垂足，得Rt△CPF（见图3）. 因为∠APD=∠CPF，△APC∽△BPD，所以CP=■，根据面积法，求出CF=■，PF=■，所以tan∠APD=2.

组3：连接BE，交CD于F点，于是得到Rt△BPF（见图4）. 因为BF=■，△APC∽△BPD，可得DP=■，PF=■，所以tan∠APD=2.

组4：我们组发现以上三组的解题思路有个共同之处，均是构造出一个直角三角形，然后再解决问题.

师：非常好！针对此题，每组成员都进行了积极的思考，运用了添加辅助线构造直角三角形的方法解决问题. 由此可见，想要解决三角函数的相关问题，前提是找到恰当的直角三角形，而后问题就迎刃而解了.

一题多解，既拓展了学生的解题思路，又在有限的时间内，通过小组合作学习的方式提高了課堂教学效率，学生在积极的思考中不知不觉就提高了思维能力，形成了良好的数学解题能力.

总之，自主合作学习的方式打破了传统的被动式学习模式，倡导学生积极参与教学活动. 通过教师的引导，学生能自主探索、研究与思考，逐渐形成良好的分析问题并解决问题的能力，有效地提升了学生的数学核心素养.