在合作探究中提升学生数学核心素养
沈伟明
摘 要:读图、识图能力是学好平面几何的基础,其中“三线八角”是学生在初中阶段接触到的第一种较为复杂的图形,教师应引导学生从复杂的图形中抽象出简单的基本图形,发展学生读图、识图能力,以提升学生的数学核心素养。
关键词:三线八角;同位角;数学抽象
中图分类号:G633.63 文献标识码:A
文章编号:1992-7711(2020)17-019-1
“三线八角”,是指在同一平面上,两条直线被第三条直线所截所形成的八个角。它是学习平行线判定和性质的基础,在今后的学习中扮演着重要的角色。因此,教师应利用几何画板,引导学生学会把复杂的图形抽象出简单的图形,以发展学生的识图、读图能力,进而提升学生数学学科核心素养。
一、“三线八角”教学难点成因
知識特点:三线八角是二线四角的拓展,涉及三条直线、八个角。信息容量大,图形变式多,图形中还充斥大量干扰因素。
知识储备:在此之前,除了学过一些简单的平面图形和立体图形的概念外,就是线段、直线、射线和角,对于图形的认识只停留在直观感知阶段,基本没有涉及图形的变式。
呈现方式:苏教版七年级教材,是在探索直线平行的条件中首次出现“同位角”概念的,是以图形为基础,采用描述式的定义方式,不同于代数中的概念多与运算相关联。
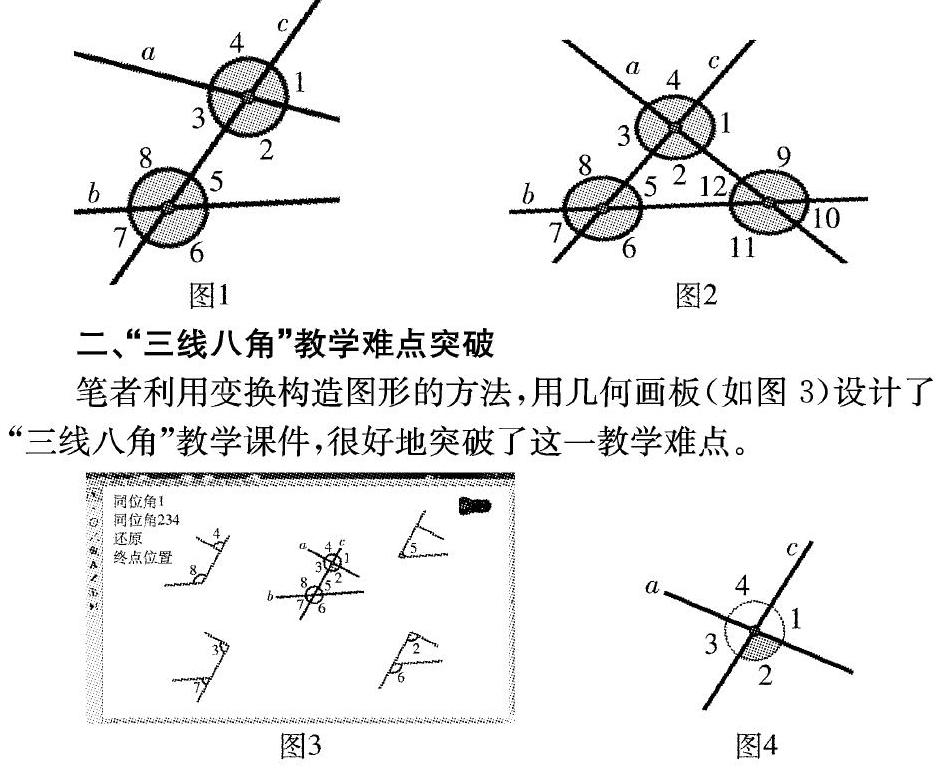
原型效应:课本上的图形是同位角的原型,比较典型与标准,而在具体练习、习题中在某些方面发生了异化。李善良教授研究表明:由于概念的“原型效应”,提到同位角的概念,学生头脑中往往出现图1,而不是图2,对于图2很多同学不能正确辨别。
二、“三线八角”教学难点突破
笔者利用变换构造图形的方法,用几何画板(如图3)设计了“三线八角”教学课件,很好地突破了这一教学难点。
三、“三线八角”教学实施策略
1.复习回顾,引入新知背景。如图4:两条直线a、c相交,请你说明∠1、∠2、∠3、∠4在位置、数量上有怎样的关系?
像这种二条直线相交所得的四个角都具有公共顶点,它们的位置、数量关系我们已经在平面图形(一)中研究过了,本课我们将研究三条直线相交所得的八个角中不具有公共顶点的角之间的关系。
2.合作交流,探究新知形成。如图1:使直线b与直线c也相交,也可以说直线a、b被直线c所截,直线a、b叫做被截线,直线c叫做截线。请你说明∠1与∠5之间的位置关系。单击“同位角”按钮,移出∠1与∠5,引导学生观察、分析同位角的位置关系,从而归纳出同位角的概念。类似地,学生模仿教师给同位角下定义的方法,很快给出了内错角、同旁内角的概念。
3.自主探索,挖掘基本图形。当图形较为复杂时,要正确找出上述三类角,其关键是能从中找出构成这对角的是哪三条直线,并分清哪一条是截线,哪二条是被截线,抽象出“基本图形”,从而进行识别。
单击“其余同位角”按钮,此时其余三对同位角从图形中慢慢移出,把同位角的形状特征动态地表现出来,让学生直观地感知同位角的“F”模型,类似地,可以引导学生探索出内错角的“Z”模型、同旁内角的“U”模型,落实了数学抽象这一核心素养。为加深学生印象,再用手势进行比划,更增加了课堂乐趣(如图5)。
4.变式练习,提升核心素养。由于受“原型效应”的影响,学生还不能从变化和复杂图形中识别这三类角,关键是没有抓牢概念的本质,对概念理解不透彻。为了突破这一困境,教师可以利用几何画板设计教学课件,为学生构建一个形象直观的动态数学情境,学生通过观察、感知、分析、归纳、发现其中“不变”本质属性,加深对概念本质的理解,培养其数学思维能力,提升核心素养。如图3,移动直线a、b以及直线c的位置,设计不同的变式图形,在动态的情景中,让学生感知到直线的位置、角的大小在变,但三类角的本质特征却不变。
本课例通过“问题情景—建立数学模型—解释、应用与拓展”的模式展开,使学生直观地感受到“三线八角“知识形成与应用过程,有效地培养了学生良好的数学思维习惯和运用数学的意识,同时,教师通过将几何画板与数学变式教学有机结合,突破了传统教学的难点,提高了课堂效率,在寓教于乐中培养学生的观察力、想象力、抽象力,促进学生数学学科核心素养的提高。
[参考文献]
[1]李善良.现代认知观下的数学概念学习与教学[M].江苏教育出版社,2005.
[2]杨桂花.基于“三线八角”的教学探究.中学数学教学参考,2019(10).
[3]魏志雄,王豫黔.几何画板数学课件制作实例教程[M].北京人民出版社,2006.
(作者单位:苏州市吴江区同里中学,江苏 苏州215000)

