基于层析成像的气液两相流相关流量测量方法

仝卫国, 朱赓宏, 顾 浩

(华北电力大学 自动化系, 河北 保定 071003)

1 引 言

多相流测量广泛应用于动力、热力、石油化工等工业领域,其流量参数的准确测量对这些行业的安全稳定运行起到了至关重要的作用。电阻层析成像技术是一种适用于测量以导电介质为连续相的多相流检测系统[1～4],基于层析成像和互相关测量技术的数字化电学成像系统已经应用在气液两相流检测中,但多应用于流型重建和识别,很难对液相流量进行准确的测量[5～8]。

为了实现气液两相流液相流量的准确测量,提出了一种基于层析成像的气液两相流相关流量测量方法。把获取的气液两相流参数与相关测量原理相结合得到气相流量;采用小波变换的图像纹理分析方法获得流型特征参数。以气相体积流量与流型参数特征为输入特征,以标准液相体积流量为输出特征,建立BP神经网络液相流量测量模型,实现对液相流量的准确测量。

2 气液两相流流量测量方法基本原理

2.1 基于相关流量测量的气相流量计算方法

相关流量测量技术是根据管道内流体流动时产生具有随机性质的“噪声”信号,将两相流中的气相局部浓度随机变化呈现出来。通过对这些噪声信号的分析,反映出流体的流动状况。其相关流量测量方法原理如图1所示。

图1 相关流量测量方法基本原理Fig.1 Basic principles of related flow measurement methods

根据“凝固”流动图形假设,被测流体在上游传感器处引起随机信号的调制机制在经过一段时延τ0后,会在下游传感器处重复出现,并引起相似的作用[9]。由此可计算出x(t)和y(t)的互相关函数Rxy(τ)：

(1)

式中：τ0为渡越时间;x(t)和y(t)为上下游的随机流动噪声信号。

在测量时,根据可知的上下游随机流动噪声信号,可以将互相关速度vc的测量转化为对渡越时间τ0的求取。由于互相关函数曲线的峰值出现在τ0处,因此,噪声信号的传播速度即互相关速度vc计算公式为：

(2)

式中L为两截面之间的距离。

在理想流动状态下,同一气泡中各点的速度相等,被测流体的体积平均流速vp可以用互相关速度vc表示。

(3)

因而,流体的体积流量Q计算公式如下：

Q=vc·A

(4)

式中A为截面面积。

2.2 基于小波变换的流型图像特征值提取方法

2.2.1 流型图像重建的Landweber迭代算法

利用电学层析成像技术中的16电极传感器进行流型图像信息的采集,采取Landweber迭代算法进行流型图像重建[10]。Landweber迭代算法的框图如图2所示。

图2 Landweber迭代算法的框图Fig.2 Block diagram of the Landweber iterative algorithm

在输出图像估计测量值时,利用实际图像测量值与估计值之间的偏差进行图像的修正,使得图像重建的偏差足够小。Landweber迭代算法公式为:

(5)

式中：gLBP为传统Landweber迭代算法;g0为传统Landweber迭代算法;迭代后的图像灰度值;gk为第k步迭代的图像灰度值;S为灵敏度矩阵;V为电压向量值;α为迭代因子。

2.2.2 小波变换的特征值提取方法

利用小波阶数N=3的正交小波变换,将一幅二维气泡流型图分解为3层进行特征抽取[11～12]。流型图像的3层小波分解如图3所示。

图3 3层小波分解Fig.3 Three-layer wavelet decomposition

计算3层小波分解后各子图像的纹理能量特征Ei和范数特征Fi的公式如下：

(6)

(7)

式中：gi(x,y)表示图像在某一点g(x,y)的小波分解系数;x,y表示像素的行值和列值;M×N表示变换后子图像素的个数;i=1,2,…,10。

把9个子图像分为3组进行图像纹理特征的抽取,g8、g9和g10为第1组;g5、g6和g7为第2组;g2、g3和g4为第3组。在水平、垂直和对角线方向对小波分解的3层图像分别进行纹理能量特征和范数特征提取。把提取的子图像纹理特征进行有效的结合,构造出6个识别参数：

这6个参数λ1、λ2、λ3、λ4、λ5、λ6分别代表各分解层次内(同一分辨率)纹理的对角方向分量与水平和垂直方向分量之和的比值。因而,这6个参数具有旋转90°、180°和270°不变的性质,这对纹理结构分类与识别是非常有利的[13]。

3 流量测量模型的建立

BP神经网络能够把一组样本的输入和输出问题有效地转变为一个非线性优化问题。BP网络由输入层、隐含层和输出层3层构成。理论证明,具有偏差和一个无限隐含层节点的3层BP网络可以实现任意从输入到输出的非线性映射。误差精度的提高可以通过增加隐含层中的神经元数目获得,其训练效果比增加层数更容易观察和调整。因此,测量模型采用具有单一隐含层的3层BP神经网络[14～15]。具有一个隐含层的BP神经网络结构如图4所示。

图4 一个隐含层的BP神经网络的结构图Fig.4 Structural diagram of a hidden layer BP neural network

神经网络具有7个样本输入特征,包含1个层析成像测得的气相体积流量与6个小波分析得到的纹理特征值,样本输出特征是标准液相体积流量。它们具有不同的单位和量纲,因此需要归一化处理。本文采用的是Matlab神经网络工具箱的归一化函数Mapminmax将样本数据归一化到[0,1]范围内,Mapminmax对测试集数据归一化计算公式为：

(8)

式中：y为归一化后的数据;x为归一化前的原始数据;σmin为归一化前数据的最小值;σmax为归一化前数据的最大值。其中隐藏层使用S型函数,设置10个隐藏层节点数;选取收敛速度快的正则化训练算法;输出层使用线性传递函数,使其能够以很小精度逼近给定函数。

4 实验结果与分析

4.1 实验环境

以气液两相流为研究对象,其中电磁流量计测量范围为0.5～70 m3/h,精度为0.5%。ERT系统数据采集使用16电极测量结构,管段直径为60 mm的垂直玻璃管道,层析成像上下两个截面之间的距离L为50 mm,数据采集速度最高200帧/s,图像在线重建速度最高500帧/s,图像分辨率为32×32像素。实验平台采用的是基于Windows 8 Intel Core i7 2.60 GHz操作系统;使用TJU-ETest软件进行流体图像采集,采用MATLAB软件进行程序编写,对气液两相流量测量模型进行试验。

4.2 基于双截面ERT系统气体流量的特征提取

以500帧的图像数据(8组数据)为例,从层析图像的上位机中获取每帧为1×812个的灰度图像数据,将图像数据按照从下到上,从左到右的顺序排列,得到层析成像图像如图5所示。

图5 层析图像截图Fig.5 Tomography screenshots

图5中每行为一帧中的1×812个数据,500帧数据按照从下到上的顺序排列。选择其中一组图像与数据分析,设阈值为0.5,对图形进行灰度二值化。通过实验处理得到的灰度值二值化图像如图6所示。

图6 层析成像二值化图Fig.6 Binary tomography

相含率是指两相流中各相所占的份额。截面相含率可以从层析成像的二值化图像中得到,即计算值为1的像素点与值为0的像素点所占的比例。本文实验中对500帧图像进行处理后得到的相含率变化曲线如图7所示。

图7 500帧数据流型相含率曲线Fig.7 500 frame data stream phase holdup curve

图8 500帧原始灰度总和的分布变化曲线Fig.8 Distribution curve of the sum of original gray scales of 500 frames

根据相关测量原理,用Matlab软件对提取的灰度值进行编程处理,得到上下游A、B两截面的500帧原始灰度总和的分布变化曲线如图8所示,通过频域傅里叶变换的FFT算法得到互相关函数曲线如图9所示。

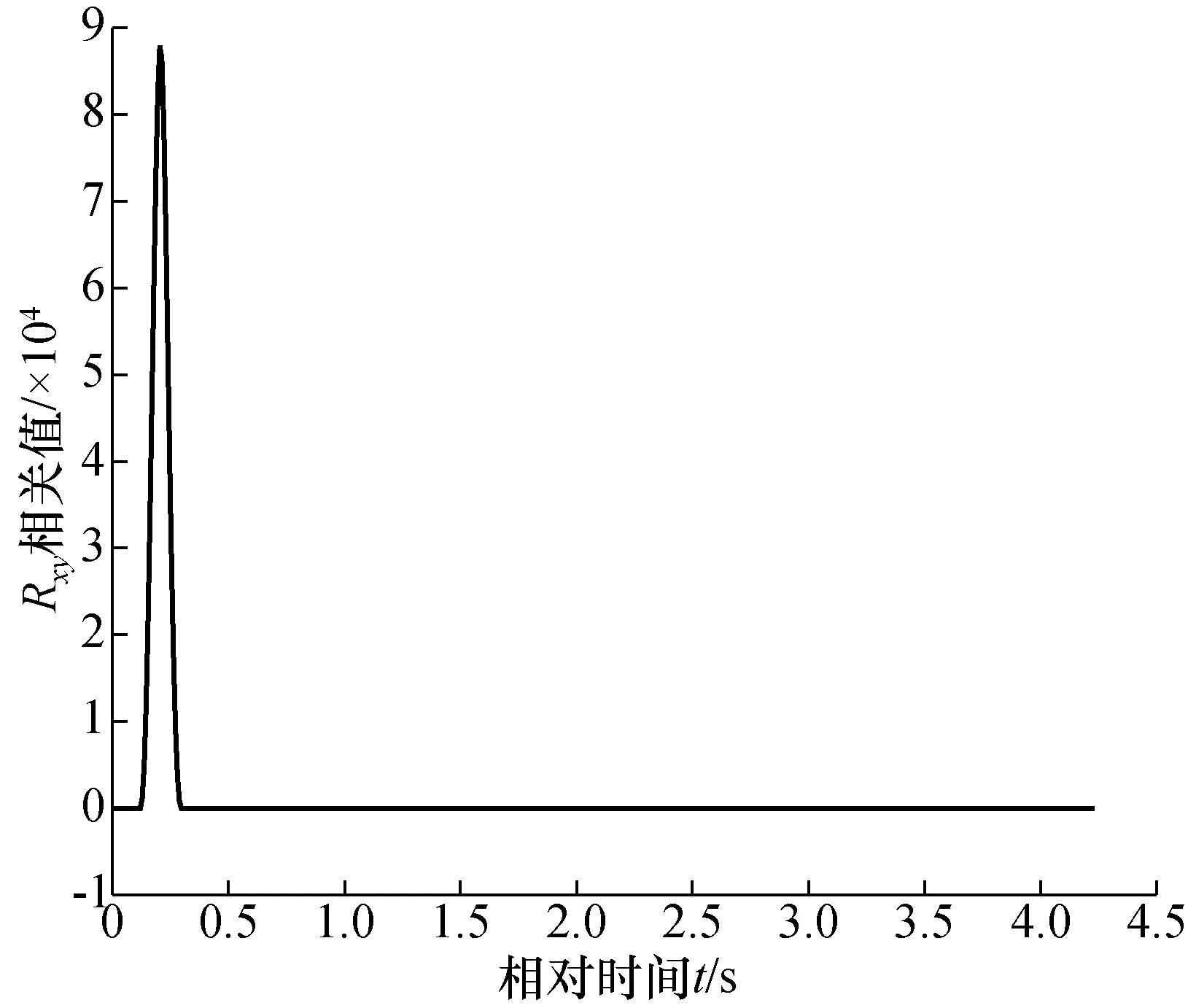
图9 500帧原始灰度互相关函数变化曲线Fig.9 500-frame original gray-scale cross-correlation function curve

根据图9中的互相关函数变化曲线峰值对应的时间位移得到渡越时间τ0,根据公式vp=vc=L/τ得到气相流体速度。把计算得到的渡越时间与TJU-ETest软件测得的渡越时间用Matlab可视化,得到500帧数据渡越时间柱状对比图,如图10所示。

图10 渡越时间柱状对比图Fig.10 Crossing time column comparison chart

根据流型渡越时间,结合气泡体积流量公式得到气相体积流量值,如表1所示。

表1 气相体积流量值Tab.1 Gas phase volume flow value m3/h

表1中：τ为渡越时间,QL为标准液相流量，QG1为泡状流气相流量,QG2为弹状流气相流量。

由于气液两相流之间流速存在滑差,因此,测得的气相流量与真实气相流量存在一定的误差。建立的液相流量测量模型是以标准液相流量作为输出特征,只需要气相流量来表示输入特征,对其测量精度要求不高,因此测得的气相流量可以满足液相流量测量模型输入特征的要求。

4.3 基于小波变换的流型图像特征值提取

对流型图像特征进行提取时,将二维气泡流型图分解为3层进行特征抽取,分别计算出3层小波分解后各子图像的纹理能量特征Ei和L1范数特征Fi,进而得出6个识别参数λ。其中泡状流和弹状流流型的3层小波分解图像分别如图11和图12所示,对应λ值如表2所示。

图11 泡状流流型图像的3层小波分解图Fig.11 Three-layer wavelet decomposition diagram of bubble flow image

表2 垂直管道泡状流型图像纹理特征参数Tab.2 Texture feature parameters of vertical pipe bubble flow pattern image

图12 弹状流流型图像的3层小波分解图Fig.12 Three-layer wavelet decomposition diagram of slug flow image

4.4 流量测量模型的性能分析

流量测量模型共有200组输入样本、200组输出样本数据。将其中150组数据分配到训练集用于神经网络模型的学习和训练,50组数据作为测试集验证模型的有效性。

进行模型训练得到训练数据迭代次数和均方误差的变化关系如图13所示;与训练梯度、参数u、交叉次数的变化关系如图14所示。

图13中,在迭代次数为6时得到最佳验证集的均方误差为0.009 76;在迭代次数为12时的训练梯度为0.006 327 1、参数u为0.000 01、交叉次数为6。

图13 迭代次数和均方误差的变化关系图Fig.13 Relationship between iteration number and mean square error

图14 迭代次数和梯度、参数u、交叉次数的变化关系图Fig.14 Relationship between iteration number and gradient, parameter u, cross number

流量测量模型的辨识效果是由训练集和预测集的均方误差、决定系数体现的,决定系数的范围在[0,1]内,均方误差越接近于0,决定系数越接近于1,说明模型性能越好,其泡状流和弹状流流量测量模型的预测结果如图15和图16所示,模型预测参数如表3所示。

从表3分析得出,弹状流和泡状流的训练集、预测集的决定系数均接近于1,均方误差均接近于0,说明气液两相流流量测量模型具有良好的预测识别能力。其中预测集的绝对误差结果如图17所示,部分绝对误差数据如表4所示。

图15 泡状流测量模型预测结果图Fig.15 Forecast result of bubble flow measurement model

图16 弹状流测量模型预测结果图Fig.16 Prediction result of slug flow measurement model

表3 训练模型参数对比Tab.3 Comparison of training model parameters

图17 预测集的误差结果图Fig.17 Error result diagram of prediction set

表4中：QL为标准液相流量;QP1为泡状流预测流量;QP2为弹状流预测流量;Δ1为泡状流预测流量相对误差;Δ2为弹状流预测流量相对误差。从图17中分析得出,泡状流和弹状流的相对误差都在3%的范围内,波动范围小,稳定性比较好。泡状流的平均相对误差为2.435%,弹状流的平均相对误差为2.221%,说明气液两相流流量测量方法是有效可行的。

表4 预测流量的相对误差Tab.4 Predictive absolute error m3/h

5 结 论

为了获得气液两相流中准确的液相流量值,采用层析成像的气液两相流相关流量测量方法,建立以气相流量值和纹理特征识别参数为输入特征的液相流量测量模型。实验结果表明,气相流量作为输入特征时测量精度要求不高,同时可以建立相对误差低于3%的液相流量测量模型。为后续研究标准气相流量和多相流参数提供了较好的参考。