VMD-Wavelet联合去噪算法研究与应用

阚玲玲, 高丙坤, 梁洪卫, 路敬祎, 王喜良

(1. 东北石油大学 a. 电气信息工程学院； b. 黑龙江省网络与智能控制重点实验室, 黑龙江 大庆 163318；2. 上汽通用汽车有限公司 南厂冲压车间, 山东 烟台 264006)

0 引 言

油气管道泄漏声波信号含有大量的噪声, 需对其进行去噪处理[1]。受信号特征、小波基函数影响, 小波算法对信噪比较小的非平稳随机信号去噪效果不明显[2]。独立分量分析法能处理小信噪比非平稳随机信号, 但使用范围受限[3], 需各分离信号为同源线性组合。EMD(Empirical Mode Decomposition), 即经验模态分解, 把信号分解为从高频到低频的一系列本征模态函数IMF (Intrinsic Mode Function)与余项的和, 通过模态挑选实现去噪, 不用选择基函数, 易于去除高频噪声[4-5], 但其去噪效果整体上不如小波阈值去噪。于金涛等[6]利用EMD-Wavelet算法对声发射信号进行处理, 取得了良好的去噪效果。然而, 将EMD去噪进行具体应用过程中发现, 该方法更适合高频振动信号的去噪[7], 由于油气管道泄漏声波信号能量集中在低频段, 在用该方法进行去噪时存在模态混叠现象[8-9]。变模态分解VMD(Variable Mode Decomposition)从低频到高频分解出各模态[10], 通过选取的有效模态重构原始信号[11], 在油气管道泄漏声波信号处理过程中可以很好地抑制EMD分解的模态混叠现象, 去噪效果更好[12]。

笔者将VMD-Wavelet联合去噪算法用于油气管道泄漏声波信号去噪处理, 通过标准信号进行仿真验证该算法的去噪优势, 对实际采集到的的油气管道泄漏声波信号采用该联合去噪算法进行处理, 取得了良好的去噪效果。

1 小波阈值去噪及其改进

小波变换法通过选择合适小波系进行重构可获得较好的去噪效果[13], 其中小波阈值去噪由于在阈值选取、构造阈值函数等方面具有优势而获得广泛应用[14]。

1.1 改进小波阈值去噪算法原理

小波阈值去噪有软、硬两种阈值函数, 其中软阈值函数表达式如下

(1)

(2)

(3)

式(3)取值如下

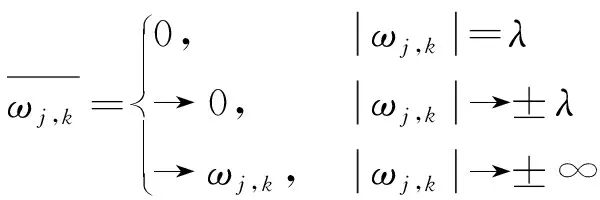
(4)

1.2 改进算法去噪效果分析

图1 去噪效果分析Fig.1 Analysis of denoising effect

将式(3)的参数进行如下设置：λ=0.6,α=1, -2≤ωj,k≤2, 各种阈值函数对比如图1所示。仿真

结果表明： 该改进算法能有效保留信号的奇异值, 远离阈值时趋近硬阈值曲线, 靠近阈值时趋近于软阈值曲线。

分别用含有2 dB高斯噪声的Heavy Sine和Bumps信号进行仿真验证, 小波基选用Danbechies小波。表1给出的实验结果表明, 改进小波阈值函数去噪算法可取得最大SNR(Signal Noise Ratio)。

2 Wavelet-EMD联合去噪

EMD算法[16]由于原始信号的高频分量和噪声包含在经EMD分解后的低阶模态中, 有效信号能量集中在高阶模态。因此, 可以通过各种判定条件挑选k值, 对前k个IMF去噪后与剩余的IMF、余项求和重构信号。由于该算法在进行信号分解过程中存在模态混叠现象[8], 因此需要与小波变换等算法结合进行联合去噪, 二者的联合去噪方法有如下3种[6]。

1) IMF-Wavelet。先EMD分解, 然后对各IMFs进行小波阈值去噪, 最后进行信号重构。

2) EMD-Wavelet。先EMD分解, 然后进行信号重构, 最后对重构信号进行小波阈值去噪。

3) Wavelet-EMD。先利用小波阈值去噪, 然后对去噪后信号做EMD分解, 最后选取有效模态进行信号重构。

选取Blocks、Bumps、Heavy sine和Doppler 4种典型信号进行仿真验证, 信号长度设置为2 048个数据点, 同时加入2 dB的噪声。由表2可以发现, 除了Bumps信号外, 小波阈值去噪优于EMD去噪； Wavelet-EMD联合去噪方法优于IMF-Wavelet、EMD-Wavelet两种联合去噪方法。

表2 去噪性能分析(2 dB)

3 VMD-Wavelet联合去噪算法及其仿真分析

VMD算法将原始含噪信号分解为一系列BLIMFs(Band Limited IMFs), 该模态函数具有稀疏特性、有限带宽, 通过挑选有效的BLIMFs进行重构, 其核心算法包括： 维纳滤波、希尔伯特变换和频率混合[10,17]。

3.1 VMD去噪原理

VMD将原始信号分解为一系列具有稀疏特性的uk(t), 其载频为ωk, 通过对挑选的有效独立模态函数进行重构实现去噪。笔者将3个余弦分量和1个加性高斯白噪声信号合称为原始信号, 即

xn(t)=cos(4πt)+1/4cos(48πt)+1/16cos(576πt)+η

(5)

其中3个余弦分量的载频分别为2 Hz(低频)、24 Hz(中频)、288 Hz(高频)。对合成信号进行VMD分解, 对其去噪效果进行分析。

VMD分解过程中将带宽α设为2 000, 采样频率fs设为1 000, 分解尺度k设为3。经VMD分解后的BLIMF分量如图2所示。图2b表明大幅值低频分量被精确分解, 图2c表明中幅值中频分量分解效果略差, 图2d说明高频弱信号的分解效果最差。

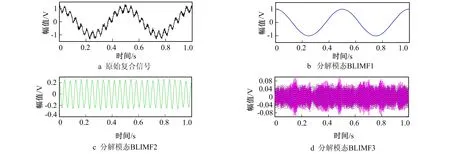
图2 VMD分解得到的3个BLIMFsFig.2 The three BLIMFs from VMD Decomposition

该合成信号经VMD分解后的频谱分析如图3所示, 该图采用双对数横坐标, 复合信号频谱无准确载频值, 2 Hz,24 Hz,288 Hz的3个余弦分量均能找到对应的频谱曲线。与EMD分解相比, VMD算法能得到更高的保真度, 具有很强的中心频率捕获能力, 可抑制模态混叠现象发生, 具有较高的抗噪声鲁棒性。

图3 3个BLIMs的频谱曲线Fig.3 Spectrum curve of three BLIMFs

3.2 VMD-Wavelet联合去噪算法仿真

如上所述, Wavelet-EMD联合去噪方法能改善单一方法的去噪效果, 基于此笔者提出VMD-Wavelet联合去噪算法, 该联合去噪算法利用Hausdorff距离和峭度作为选取有效模态的依据, 用第1节提出的改进小波阈值函数对剩余模态进行消噪, 最后对去噪处理后的信号进行重构。

3.2.1 基于Hausdorff距离的模态选取

Hausdorff距离能用于描述一维信号概率密度函数之间的相似度[18-19],P和Q两个点集之间的Hhd(即Hausdorff Distance)定义如下

Hhd(P,Q)=max(D(P,Q),D(Q,P))

(6)

采用Hhd选取模态的步骤如下。

1) 用VMD算法将原始信号x(t)分解为K个BLIMFs。

2) 计算每个BLIMF与x(t)的概率密度函数(PDFL: Probability Density Function)之间的Hhd, 用L(i)表示每个BBLIMF与原始信号x(t)相似度。

L(i)=Hhd[pPDFL(x(t),pPDFL(BBLIMFi(t)))]

(7)

3) 计算相邻BBLIMFs与原始信号x(t)的HD增量θ, 选取θ值最大的BBLIMF作为突变点

θi=L(I+1)-L(i),m=arg maxθi,i=1,2,…,(N-1)

(8)

突变点之前的模态为有效模态, 突变点之后的模态为噪声。

4) 设BBLIMFm为有效模态突变点, 则重构信号

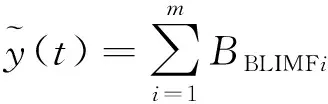
(9)

3.2.2 峭 度

峭度用于描述信号波峰尖度, 反映信号的分布特征[20-21], 其表达式

思雨差一点把事情都跟欣竹说出来。他好后怕，如果说出来，也许会被公司的人笑掉大牙的，也许会被公司的人误解的。那可真就是越理越乱了。

(10)

其中K为峭度值、μ为x的标准差、σ为x的均值、E(t)为t的数学期望。分析发现油气管道泄漏声波信号的峭度值与所含噪声有关, 因此为了减少重构信号失真, 可利用峭度值对VMD分解后BLIMFs进行二次选取。

3.2.3 VMD-Wavelet联合去噪流程

笔者将VMD和改进小波阈值去噪算法结合, 利用HD距离和峭度进行有效模态挑选, 提出了VMD-Wavelet去噪算法, 其流程如图4所示, 具体执行步骤如下：

图4 VMD-Wavelet算法流程Fig.4 Algorithm flow of VMD-Wavelet

1) 对原始信号进行VMD分解, 得到K个BLIMFs；

2) 计算相邻BLIMFs与原始信号的HD增量θ, 以增量最大的BLIMF为有效模态挑选的临界值；

3) 计算突变点之后的各BLIMFs的峭度值, 利用改进的小波阈值函数对峭度值大于选定阈值的BLIMFs进行高频去噪；

4) 将根据HD、峭度挑取的有效BLIMFs, 及经过改进小波阈值去噪后的剩余BLIMFs相结合进行信号重构。

3.2.4 VMD-Wavelet联合去噪性能分析

用含2 dB高斯白噪声、长度为2 048位的Blocks、Bumps、Doppler和Heavy Sine 4种典型信号验证VMD-Wavelet算法去噪效果, 仿真结果如表3所示。

表3 VMD、Wavelet联合去噪性能分析

表2、表3的仿真结果表明： 笔者提出的VMD-Wavelet联合去噪算法对4种典型信号去噪时均取得最佳的峰值信噪比, 最小的均方误差, 去噪效果优于Wavelet-VMD, 同时, 也优于EMD、Wavelet相结合的联合去噪算法。

4 VMD-Wavelet在油气管道泄漏声波信号去噪中的应用

下面运用VMD-Wavelet算法对油气管道泄漏声波信号进行去噪处理。图5为低背景噪声时原始含噪信号和重构信号波形, 经VMD-Wavelet去噪重构后SNR为14.00 dB, MSE为0.013 V。

图6为利用VMD-Wavelet算法对实际运行的天然气管道在强背景噪声环境下所采集的大、小两种泄漏声波进行去噪后的波形, 大泄漏声波信号SNR为64.34 dB、MSE为0.000 8 V, 小泄漏声波信号SNR为50.31 dB、MSE为0.000 24 V。仿真结果表明： VMD-Wavelet联合去噪算法对强背景噪声下的泄漏声波信号具有很好的去噪效果, 可实际应用于油气输送管道的泄漏声波信号预处理。

图5 低背景噪声下小泄漏声波信号去噪效果Fig.5 Analysis of the performance of acoustic signal denoising in ideal state

图6 大噪声环境下泄漏声波信号去噪效果图Fig.6 Time domain waveform of leakage acoustic signal denoised by VMD-Wavelet in noisy environment

5 结 语

笔者通过Wavelet-EMD联合去噪的思想, 对小波阈值函数进行改进, 结合VMD分解, 提出了VMD-Wavelet联合去噪方法。该算法利用HD、峭度作为有效模态挑选的判定条件, 利用含噪的4种典型信号验证VMD-Wavelet的去噪效果, 仿真结果表明该联合去噪算法的SNR、MSE均优于常见去噪算法； 将该联合去噪算法应用于天然气管道泄漏声波信号处理, 发现在强背景噪声下该算法能获得很高的信噪比改善和很小的均方误差。