基于Copula理论和高斯混合近似的半不变量研究
王金玉, 赵梓翔, 孙伟丹
(1. 东北石油大学 电气信息工程学院, 黑龙江 大庆 163318;2. 大庆石油管理局 大庆油田力神泵业(太仓)有限公司, 江苏 苏州 215400)
0 引 言
概率潮流是评价当前和未来电力系统性能的重要决策工具[1]。确定性潮流完全忽略了输入不确定性。在输电层插入可再生能源, 如光伏发电, 增加了电力系统的不确定性水平。在传统发电中, 不确定性源于强迫停运率[2], 而在光伏发电中, 不确定性源于气候变化导致的太阳辐照度预测不准确[3]。另一方面, 负荷需求的不确定性来源于预测和测量误差。概率潮流通过将每个输入看作一个随机变量综合这些不确定性的影响。
目前, 概率潮流的主要方法包括模拟法、解析法和近似法。模拟法又称蒙特卡洛仿真法(MCSM: Monte Carlo Simulation Method), MCSM需要大量的模拟以计算精确的结果[4]。但MCSM存在收敛速度慢, 计算时耗长、代价大等缺点。针对MCSM的不足, 丁明等[5]提出拉丁超立方和MCSM相结合的方法, 提高了采样效率。陈伟等[6]提出了以组合抽样MCSM的概率潮流计算方法, 该方法采样效率高, 收敛速度快, 但缺点是未能涉及分布式电源的相关性问题。近似法是根据已知输入随机变量的概率分布, 求取输出随机变量各阶矩的概率统计方法[7], 该方法计算速度快, 但计算量随着随机变量数目的增加而增加[8]。解析法包括了卷积法和半不变量法(PLF-CM: Probability Load Flow Based on Cumulant Method), 其中PLF-CM是在卷积法的基础上提出的, 半不变量法的优势在于计算量少, 只需在基准点处进行一次确定性的潮流计算; 缺点是输入变量必须保持相对独立, 当功率波动较大时仅在基准点处展开, 存在较大误差。针对以上缺点, 朱星阳等[9]提出分段线性化减少误差, 再从半不变量定义出发, 推导出分段线性函数因变量与自变量的半不变量之间的定量关系。缺点在于假设输入变量相互独立且在输入变量的概率密度函数未知时, 不能满足定义推导的条件。
笔者采用高斯混合近似建立多模式分布, 用半不变量计算代替卷积运算, 引入Copula理论构建具有相关性输入随机变量的概率分布模型。这种技术节省了实现卷积运算的时间, 并且进一步有效地合并了多个输入相关性, 而且不受输入随机变量的边缘分布类型及是否线性相关的限制。考虑了输入的高斯分布、非高斯分布和离散分布的混合。还讨论了多个输入相关案例。通过与Gram-Charlier法(CCGCM: Copula Combined Cumulant and Gaussian Mixture Approximation Method)、Cornish-Fisher法(CCCFM: Combined Cumulant and Gram-Charlier Method)、卷积法(CM: Convolution Method)和MCSM的比较, 评价了改进半不变量的有效性。
1 概率潮流模型
由n条母线组成的电力系统, 基本线性化潮流模型[10]如下
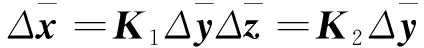
(1)
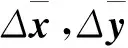
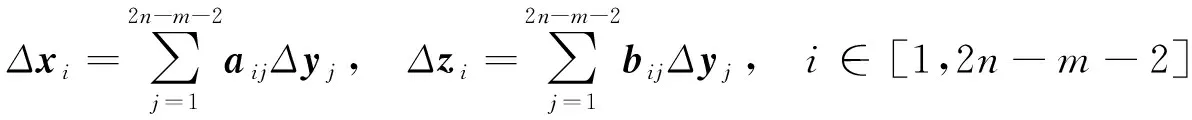
(2)
其中aij和bij(K1和K2的元素)为灵敏度系数,m为系统中PV(Power Voltage)总线的总数。式(2)中的向量xi和zi的元素如下
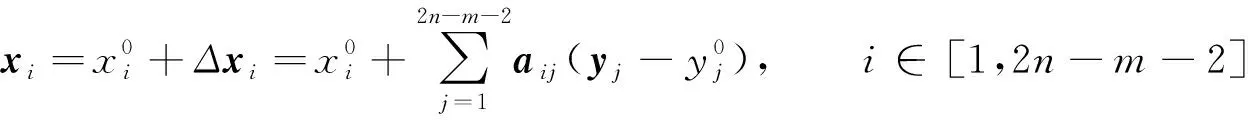
(3)
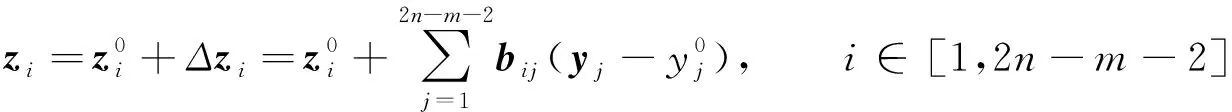
(4)
其中x0、y0和z0分别为x、y和z的期望值。式(3)和式(4)联立, 得
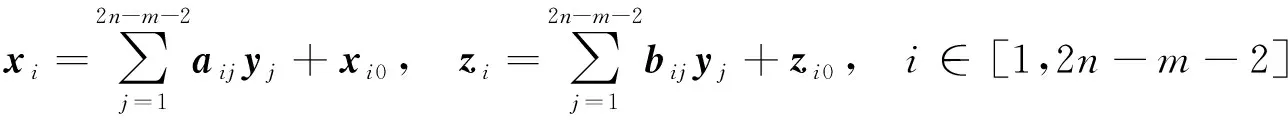
(5)
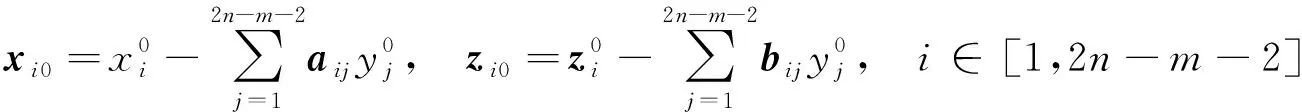
(6)
进一步简化式(5), 得
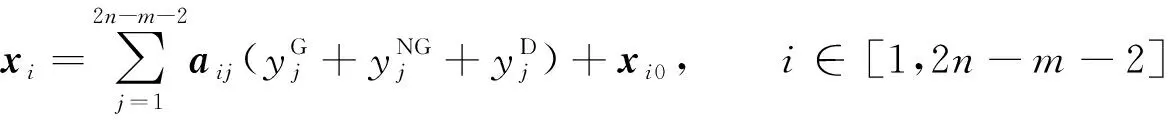
(7)
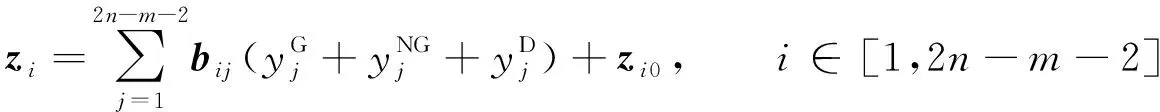
(8)
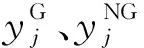
2 半不变量高斯混合近似法求解概率潮流
2.1 Copula理论
假设n个随机变量X1,X2,…,Xn的边缘分布函数分别为F1(x1),F2(x2),…,Fn(xn), 其联合分布函数为H(X1,X2,…,Xn), Copula函数是描述边缘分布和联合分布的连接函数。即有
F(x1,x2,…,xn)=C(F1(x1),F2(x2),…,Fn(xn))
(9)
其中C为Copula连接函数。
Copula函数的种类繁多, 考虑其计算精度和计算难度, 当前应用最为广泛的Copula函数共两大类: Archimedes Copula函数(包括Frank、Gumbel和Clayton Copula函数等)和椭圆Copula函数(包括正态和t-Copula函数等)。其中Archimedes Copula函数在收敛率和收敛速度上普遍优于椭圆Copula函数。
对Copula函数的求取, 笔者采用基于核密度估计的最短距离法, 用
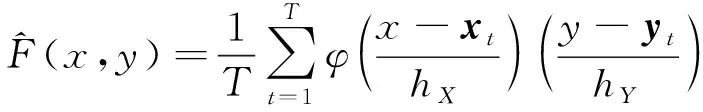
(10)
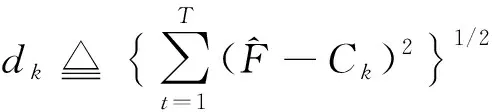
(11)
2.2 高斯混合近似法
非高斯总线功率y的概率分布可近似为g阶高斯和[12]如下
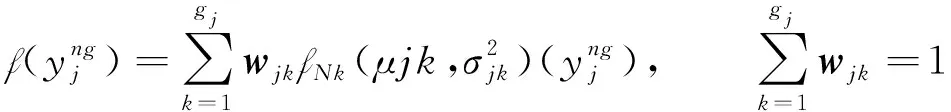
(12)
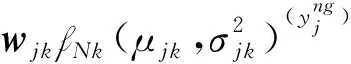
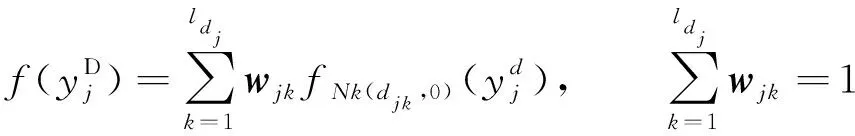
(13)
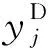
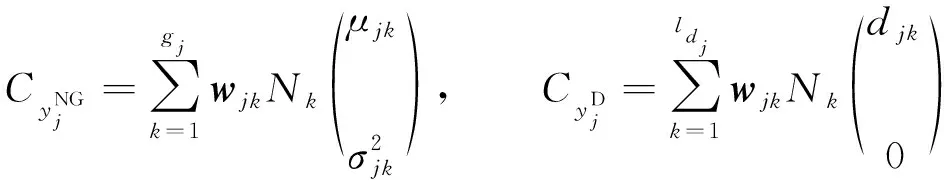
(14)
假设式(12)和式(13)中逼近所需随机变量的高斯分量的总数为Nr,Nr的值为所有与非高斯总线功率相关的高斯分量的数量和离散总线功率中存在的脉冲总数的乘积。因此, 期望随机变量的分布可以由Nr中得到的高斯分量分布的加权和建立。在每次评估中, 等效概率权重是评估所有高斯分量的概率权重的乘积。
2.3 输入相关线性组合的半不变量
皮尔逊积矩相关系数矩阵与正扩展无关。但与负扩展有关。如果是负扩展, 则其就会改变[13]。由于aij和bij是正的或负的, 因此,nr相关输入与皮尔逊积矩相关系数矩阵(ρx)nr×nr的线性组合被推广为
Y=±X1±X2±…±Xnr
(15)
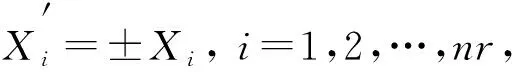
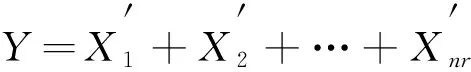
(16)
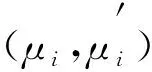
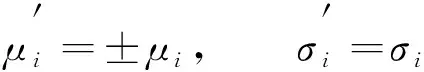
(17)
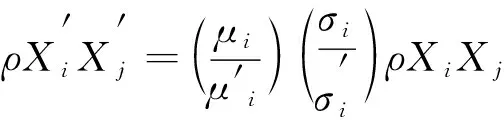
(18)
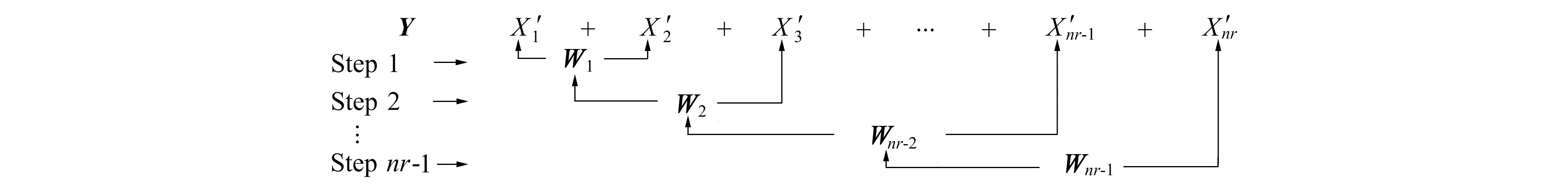
图1 相关输入随机变量的线性组合Fig.1 Linear combination of related input random variables
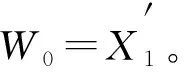
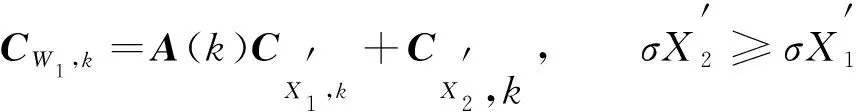
(19)
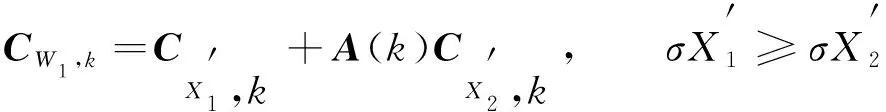
(20)
其中A(k)=(1+ρ)k-ρk
(21)
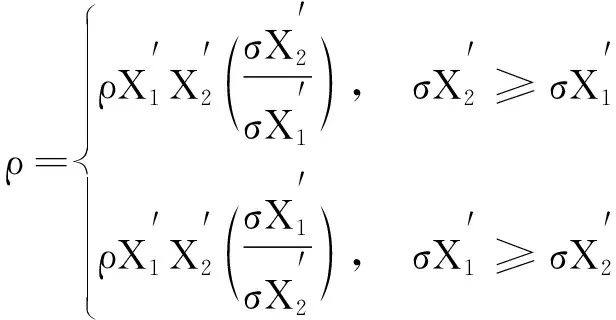
(22)
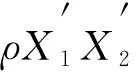
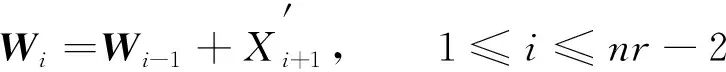
(23)
由此, 可得计算半不变量的参数
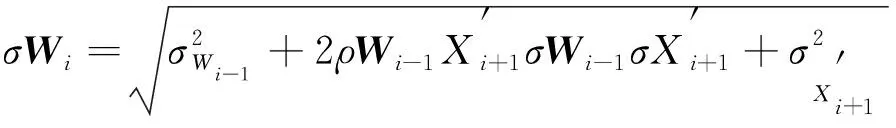
(24)
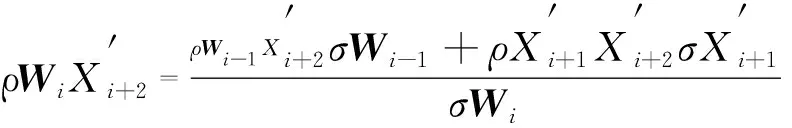
(25)
3 Copula函数结合高斯混合近似的半不变量法概率潮流计算
基于Copula函数结合高斯混合近似的半不变量法的核心在于根据输入变量的初始样本构建Copula联合分布模型并求得条件分布函数及产生满足相关条件的独立样本, 以简化为线性的交流潮流方程为基础, 再根据高斯混合近似, 在不使用任何级数展开方法的情况下, 精确地得到了与这些输入相关的多模母线电压和线路功率流的概率分布。同时, 考虑了多输入相关性, 进一步有效地合并了多个输入相关性, 而且不受输入随机变量的边缘分布类型及是否线性相关的限制。最后精确地得到了与这些输入相关的多模母线电压和线路功率流的概率分布。
计算步骤如下:
1) 根据光伏的历史测量数据采用非参数核密度计算每个光伏穿透水平的分布函数;
2) 根据光伏间的相互关系, 按2.1节的方法选择合适的Copula函数;
3) 根据Copula理论建立随机变量的联合概率分布并采样, 即先对一个变量均匀采样, 其后对另一个变量在条件概率分布下采样;
4) 求取其他不相关性的输入量的半不变量;
5) 根据2.3节的方法合并多个输入相关性变量;
6) 最后根据高斯混合近似半不变量法获得输出量的概率密度函数和累计概率分布曲线。
4 仿真分析
在Matlab平台上使用改进的IEEE 14和IEEE 57节点系统对Copula理论结合高斯混合近似法求解半不变量进行了验证。检验Copula理论结合高斯混合近似处理多输入相关的能力。求解精度和计算效率两个性能指标。其中详细参数见文献[16]。光伏穿透水平根据本地总线负载需求确定。在应用高斯混合近似时,gj的值被认为是2。假设属于两个不同非高斯总线功率的高斯分量之间的皮尔逊积矩相关系数与非高斯总线功率之间的皮尔逊积矩相关系数相同。采用以下约定指定所需的随机变量: |Vi|和δi分别是第i条母线上的母线电压幅值和电压角。PLi-j和QLi-j分别是连接总线i和j的线路中的实际功率和无功功率。估计任意期望随机变量X的标准差(σ)的绝对百分比误差
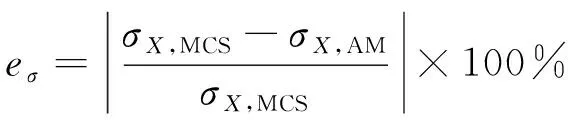
(26)
其中σX,MCS和σX,AM分别是使用蒙特卡洛和分析方法获得的X的标准偏差。
4.1 IEEE 14节点系统
概率潮流采用Copula理论高斯混合近似法(CCCGMA: Copula Combined Cumulant and Gaussian Mixture Approximation Method)、半不变量Gram-Charlier法(CCGCM)、半不变量Cornish-Fisher法(CCCFM)、卷积法(CM)和蒙特卡洛模拟法(MCSM)。当应用Copula理论高斯混合近似时,Nr的值为所有与非高斯总线功率相关的高斯分量的数量和离散总线功率中存在的脉冲总数的乘积,Nr为1 600。在CM中, 离散序列的序列间隔被设置为0.000 1。在应用CCGCM、CCCFM时, 考虑了期望随机变量的前6个累积量。具有20 000个数据样本的MCS足以产生最小的结果变化。图2和图3分别比较了使用上述方法的14节点电压、线路7-9有功潮流的累积概率图。
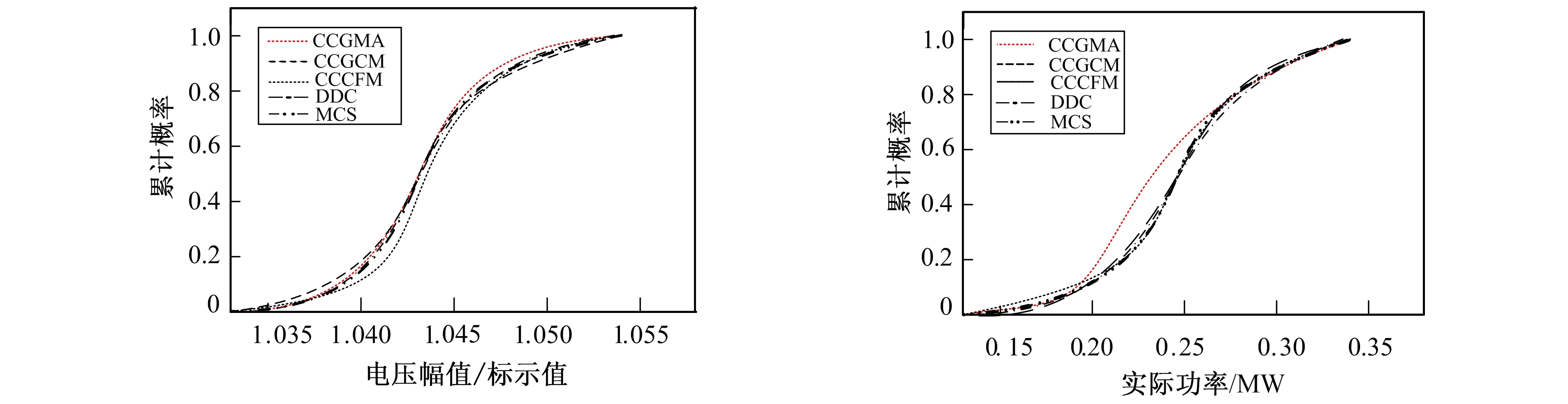
图2 14节点系统中节点14电压 图3 14节点系统7-9号线有功潮流 Fig.2 Node 14 voltage of IEEE14 node system Fig.3 Line 7-9 active power of IEEE14 node system
从图3可以看出, CCGCM使总概率值大于单位概率, 而CCCFM不能准确反映分布中的偏度和峰度参数。表1比较了CCGMA的性能。平均时间按总时间与期望随机变量总数之比计算(14总线系统为62)。使用所有分析方法获得任意期望随机变量分布所需的平均时间小于MCS。但CM的总时间超过MCS。CCGMA、CCGCM和CCCFM的平均时间基本相同。此外, 与CCGCM和CM相比, CCGMA的平均eσ较小。因此, CCGMA对于近似多模分布是准确和有效的。然而, 在没有离散输入的情况下, CCGCM和CCCFM是更好的选择。

表1 CCGMA在14节点总线系统中的性能比较
为了解多重输入相关性对期望随机变量分布的影响, 表2确定了3个相关条件。母线5、13和14处的负载功率因数假定为常数。C-3相关性对|V13|和δ13的概率密度图的影响如图4所示。表3比较了C-1、C-2和C-3相关性对平均值(μ)、标准差(σ)、偏度(γ1)和峰度(γ2)的影响。可以看出相关性对μ没有任何影响。但其对σ、γ1和γ2的影响相当显著。皮尔逊积矩相关系数的恒定变化导致σ、γ1和γ2几乎恒定变化。
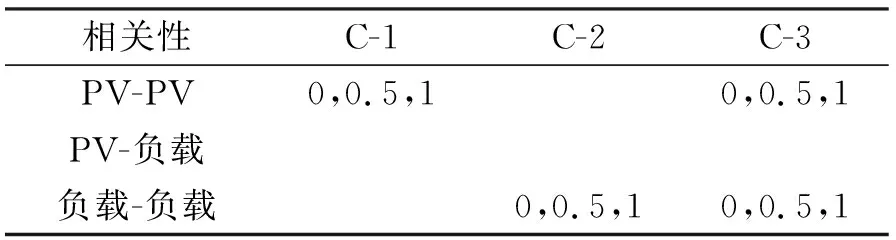
表2 不同的相关条件

图4 4C-3相关性对13母线电压和13母线电压角的影响Fig.4 Effect of C-3 correlation on node 13 voltage and node 13 voltage angle
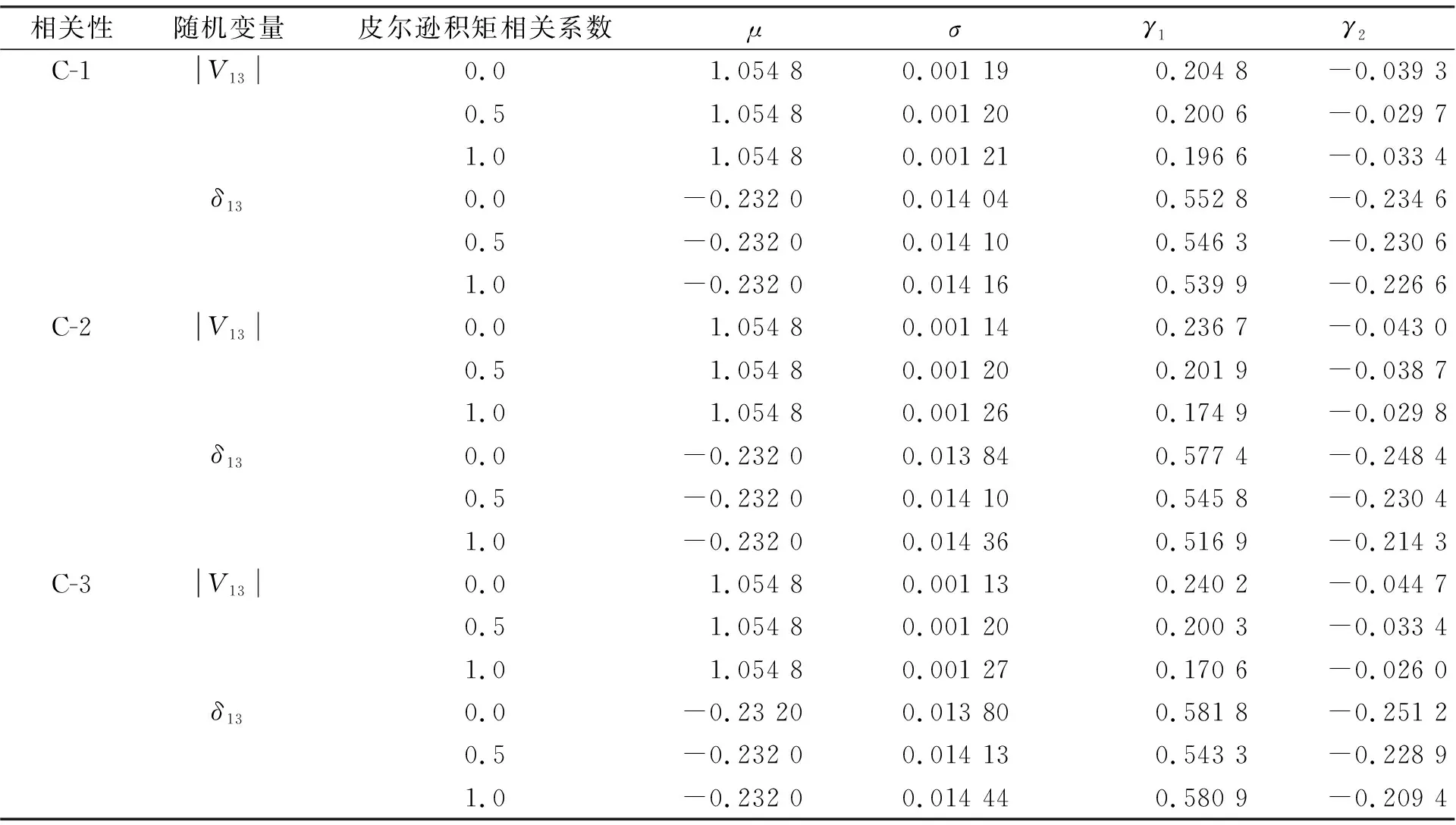
表3 不同相关条件的影响
4.2 IEEE 57节点系统
假定母线13、14、15、16和17处的实际和无功负荷功率服从高斯分布。输入和期望随机变量的总数分别为26和266。概率潮流PLF(Probabilistic Load Flow)采用CCCGMA、CCGCM、CCCFM、CM和MCS。K1和K2中表示(|Vi|,QLi-j)和注入实际总线功率以及(σi,PLi-j)和注入无功总线功率之间耦合的元素小于0.005, 因此被忽略。在应用CCGMA时,Nr为5 120。图5和图6分别比较了使用上述方法的δ16和PL12-16的累积概率图。
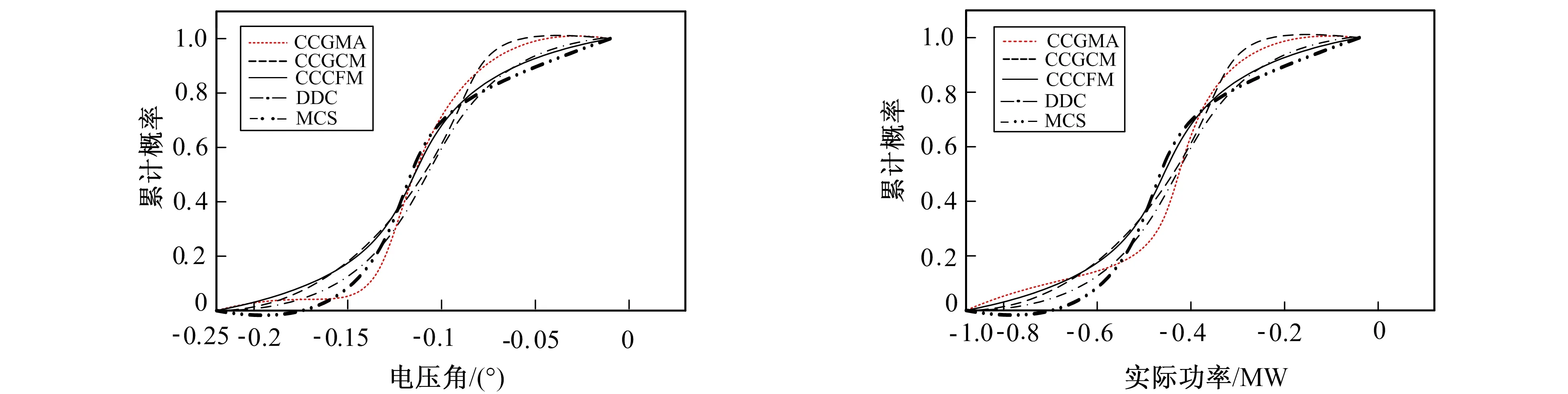
图5 57节点系统16节点电压角 图6 57母线系统12-16号线实际潮流比较 Fig.5 Node 16 voltage angle of IEEE 57 node system Fig.6 Line 12-16 active power of IEEE 57 node system
通过比较图5和图6中的曲线, 可得出与14总线系统相似的结论。CCCGMA和CM峰值分布与14总线系统大致相同, 而CCGCM和CCCFM在近似多峰分布方面是不准确的。表4比较了57总线系统的CCCGMA性能。虽然CCGCM和CCCFM的平均eσ较小, 但它们在近似多模分布时效率较低。与CM和MCS相比, CCCGMA的仿真运行时间较短。对比CCGCM、CCCFM、CM、MCS算法运行时间分别降低76%、85%、521%、97%。它还能近似地模拟所需随机变量的多模态分布。因此, CCCGMA能准确有效地建立期望随机变量的多模态分布。

表4 CCGMA在57节点系统中的性能比较
5 结 语
笔者提出的Copula结合高斯混合近似半不变量分别在IEEE 14和IEEE 57节点系统实验。与传统发电、光伏发电和系统负荷需求相关的输入不确定性被建模为相关的输入随机变量。有效地合并了多个输入相关案例。结果与CCGCM、CCCFM、DDC和MCS进行了比较。CCGMA精确地建立了期望随机变量的多模态分布, 而CCGCM和CCCFM未能精确地得到分布。DDC也被发现是准确的, 但计算时间相对较长。研究了两个系统不同相关值对期望随机变量的影响。需要注意的是, 相关性对二阶和高阶矩有显著影响, 而不影响平均值。最后, CCGMA还可以应用于其他电力系统不确定性分析问题, 如可靠性评估。

