分数阶时滞系统的Smith预估分数阶PI控制
韩 巍, 高丙坤, 郭浩轩
(东北石油大学 电气信息工程学院, 黑龙江 大庆 163318)
0 引 言
分数阶微积分完善了以往整数阶积分与微分, 提供了一种更精确的建模方式, 用以描述现实控制系统, 因此近年来分数阶系统的研究越来越受到关注。分数阶系统稳定作为非线性科学的一个重要课题得到了广泛的发展, 已经在安全通信、经济学、化学、物理和生物逻辑系统以及神经网络等领域得到了研究[1-3]。
尽管各类复杂控制策略的理论层出不穷, PID(Proportion Integral Derivative)控制依然在实际生产过程中被广泛应用。分数阶PID控制已有较多文献报道[4-6]。Podlubny[7]研究了PIλ以及PIλDμ控制器, 并得出了分数阶PID控制器与经典PID控制器相比能得到较好的系统响应。文献[8]基于模糊方法研究了分数阶模糊PID控制系统。文献[9-10]研究了分数阶PID控制系统的参数整定问题。文献[11]基于分数阶PID控制器解决了球罐液位控制的问题。严格意义上, 实际生产过程中的系统均存在时滞现象, 系统时滞对控制系统会造成不利的影响, 使系统的控制变得更为复杂。在工业控制过程中, 被控对象或多或少存在一定的纯滞后特性, 纯滞后特性往往使系统稳定性降低, 动态性能变坏, 可能引起超调和振荡; Smith预估器的引入很好地补偿了大迟延对象的纯滞后特性, 提高了系统的稳定性和动态性能。对以稳定性为首要要求、快速性为次要求的系统, 史密斯预估器十分有效。
为了研究分数阶系统的时滞问题, 笔者首先对分数阶系统PI控制进行稳定研究, 通过稳定分析推导出分数阶阶次对系统稳定时间的影响。其次对含有时滞的分数阶系统设计Smith预估PI控制器实现了系统的稳定控制, 并给出了较为简单的参数整定规则。最后通过数值仿真, 验证了所设计控制策略在分数阶时滞系统中具有良好的控制效果。
1 研究问题
1.1 问题说明
考虑如下分数阶时滞被控系统的传递函数

(1)
其中K为被控对象增益, 考虑不失系统的一般性K可设为1;α为系统分数阶系数, 为正实数;T为系统参数; e-τs为系统时滞项。

图1 控制原理
Fig.1 Control principle
G
c
s
Y
s
R
s
为研究上述稳定控制问题, 需要引用如下引理。


引理2[12]函数f(t)的α阶Riemann-Liouville导数定义如下
其中n-1<α 引理3[12]函数f(t)的α阶Caputo导数定义如下 其中n-1<α 由于分数阶系统(1)含有时滞项, 为有效控制系统, 笔者引入有Smith预估补偿控制策略, 该控制系统框图设计如图2所示。 图2 Smith预估控制原理Fig.2 Smith predictor control principle Gc(s)为分数阶控制器, 依据Smith预估控制的基本理论, 则有等效被控对象的传递函数为 W0(s)=G0(s)e-τs+G0(s)(1-e-τs)=G0(s) (2) 由式(2)看出, Smith预估控制可以有效消除系统中的时滞项。 为有效控制系统达到控制目标函数R(s), 设计分数阶PIλ控制器如下 (3) 系统没有时滞时, 系统函数 (4) 定理1 在控制器(3)作用下, 没有时滞的一阶分数阶系统(4)能有效达到目标函数R(s)。 证明 在控制器(3)作用下系统传递函数为 (5) 其中0<α<2,b≠0,ωn>0。当-cos(απ/2)<ξ<1时, 确保系统(5)是BIBO(Bounded Input Bounded Output)稳定的。 系统(5)可整理为如下形式 (6) 其中r*、λ*是r、λ的共轭转置, 并且有 (7) 式(6)右侧第1项的Laplace逆变换为 h1(t)=rtα-1Eα,α(λtα) 这里Eα,β表示双参数Mittag-Leffler函数 (8) 传递函数G(s)的脉冲响应为 阶跃响应终值可表示为 对双参数Mittag-Leffler函数(8), 当0<α<2,β是任意的复数时有 其中p≥1是任意的整数,O(·) 为高阶项。因而y(t)可表示为 (9) 稳态误差 (10) 系统有时滞时, 系统函数 (11) 定理2 在控制器(3)和Smith预估控制共同作用下, 有时滞的一阶分数阶系统(11)能有效地达到目标函数R(s)。 证明 Smith预估控制作用下 W0(s)=G0(s)+G1(s)(1-e-τs)=G1(s) 在控制器(3)作用下系统传递函数为 (12) 为分析系统的稳定性, 对式(12)进行因式分解得 其阶跃响应为 则 (13) 由式(13)可知, 随着时间t的增加, 稳态误差Eess(t)逐渐趋于0, 所以定理2成立。在满足系统稳定的情况下,ki越大, 系统越快达到其稳态值。 综上分析, 给出如下分数阶PI控制器参数整定的简单规则: 1) 依据式(5)确定一个合适的kp, 并确保系统满足BIBO稳定条件; 2) 选择一个尽可能大的ki, 确保系统快速稳定; 3)kp,ki的选择也要依据系统的特性参数及经验方法综合选定; 4) 分数阶阶次α的选择会直接影响系统的收敛速度,α越大系统的收敛时间越短。 为验证所设计控制策略有效性, 进行了如下数值仿真针对二阶分数阶时滞系统 其中T=2,τ=1,α=0.9, 则系统时滞时间为1 s, 系统阶次为0.8阶。当系统只采用分数阶PI控制时, 选择kp=0.9,ki=1, 仿真结果如图3所示。 图3 无Smith预估控制状态变量 Fig.3 The state variable without Smith predictor control 从仿真结果可以看出, 当系统含有时滞项时, 单纯分数阶PI控制下的系统状态与目标函数具有较大差距, 且状态不稳定。所以有必要采取Smith预估控制策略, 实现分数阶时滞系统的控制。 基于Smith预估控制策略, 结合参数整定规则, 选择kp=3,ki=30, 设计Smith预估分数阶PI 控制策略如图4所示, 仿真结果如图5所示。 从图5中可以看出, 系统在Smith预估控制策略作用下, 系统在时滞1 s后很快达到目标, 且趋于稳定。与图4比较, 含有Smith预估控制策略的分数阶PI控制具有更好的控制效果, 所以在分数阶时滞系统中, Smith预估分数阶PI控制策略比分数阶PI控制具有更好的可适用性。 为研究系统阶次对收敛时间的影响, 利用上述系统及Smith预估控制策略, 同时改变系统阶次。为更好地进行比较, 将各阶次的输出曲线及含有带有时滞的目标曲线绘入同一图中, 仿真结果如图6所示。 图4 Smith预估分数阶PI控制策略Fig.4 The PI control strategy with Smith predictor control 图5 Smith预估下状态变量 图6 不同阶次的系统响应曲线 Fig.5 The state variable with Smith predictor control Fig.6 System response curves of different orders 从图6中可以看出, 系统在Smith预估控制策略作用下, 不同阶次系统收敛时间不同,α较小时, 稳态误差Eess(t)具有更快的收敛速度。 笔者给出了Smith预估分数阶PI控制策略, 实现了一类含有时滞的分数阶系统稳定控制, 通过对分数阶控制系统进行特性分析, Smith预估分数阶PI控制有效克服了时滞对分数阶控制系统的不利影响。通过分析给出了分数阶PI控制器参数整定的简单规则, 仿真验证了Smith预估分数阶PI控制对系统时滞具有很好的控制效果, 且分数阶的阶次对系统稳定控制时间具有一定影响。1.2 Smith预估补偿控制

2 控制器的设计
2.1 无时滞系统时分数阶PIλ控制
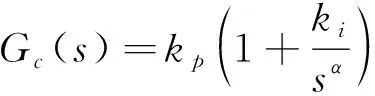
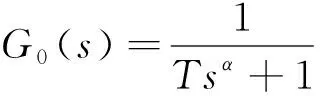


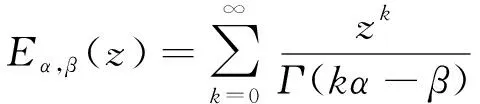


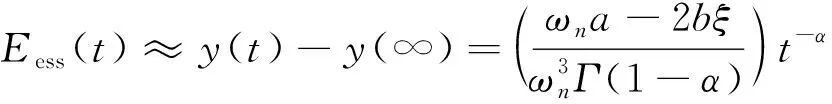
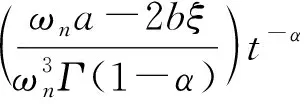
2.2 有时滞系统时Smith预估补偿控制
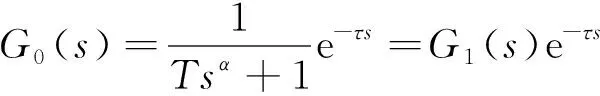
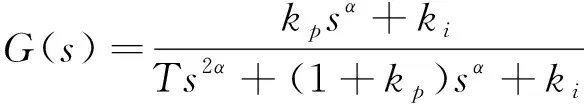

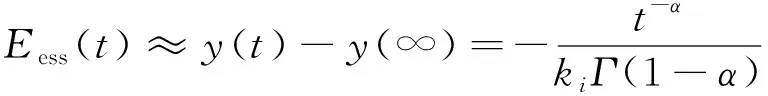
3 数值仿真



4 结 语

