量子教学优化算法及在函数优化中的应用

石 彤, 李盼池

(东北石油大学 计算机与信息技术学院, 黑龙江 大庆 163318)

0 引 言

随着现代科学技术的发展, 在进行科学研究以及工程应用时经常会遇到大量大规模非线性优化问题。经典的解析方法解决这类问题不仅需要目标函数连续可导, 往往还需要计算复杂的高阶导数, 这无疑增加了求解难度, 因此智能优化算法应运而生。一般来说, 智能优化算法是通过对生物智能、自然现象或物理规律建模而设计的随机搜索算法, 也称 “元启发式方法”[1], 如遗传算法(GA： Genetic Algorithm)[2]、差分进化(DE: Differential Evoluntionary)[3]、粒子群优化(PSO: Particle Swarm Optimization)[4]和人工蜂群算法 (ABC： Artificial Bee Colony)[5]等。

教学优化算法(TLBO： Teaching-Learning-Based Optimization)是基于教师与学生之间的交互而产生的一种新型群智能优化算法[6], 因其具有求解速度快、寻优能力强、以及没有自身的控制参数等优点, 已在各类工程优化问题中获得了很多成功应用。该算法包含两个过程： 学生互学、向教师学习。两个过程交互进行, 逐渐逼近优化问题的全局最优解。在该算法的改进方面, 文献[7]通过在教师阶段加入扰动机制, 在学生阶段加入了学生自我反思策略, 设计了一种改进的教学优化算法。然而由于该算法复杂度过高, 导致运行时间过长。文献[8]通过在教师阶段引入线性变化的学习因子, 一定程度上提升了算法的性能, 但同时算法也容易导致早熟收敛。文献[9]通过在向教师学阶段中加入精英保留机制, 在学生互学阶段加入对立学习机制, 提出精英教学优化算法(ETLBO： Elitist-TLBO)。该算法在寻优精度及速度上有所改进。文献[10]通过引入差分进化算法中的变异和交叉策略以及在学生阶段引入学生反馈机制, 设计了改进算法(ITLBO： Improved-TLBO)。算法的优化能力虽有所提高, 但算法运行时间过长。文献[11]将多目标自适应机制与教学优化算法相融合, 提出多目标教学优化算法。该方法的寻优能力有所改进。文献[12]通过修改教学阶段和学习阶段的学习行为, 提出了一种修改算法(MTLBO： Modified-TLBO), 提高了算法的全局搜索性能。文献[13]通过设计3种算子可行解发生器、教师相位算子以及学习者相位算子, 提出了一种简化教学优化算法(STLBO：Simplified-TLBO)。算法的优化能力虽有所提高, 但计算复杂度也随之增加。

量子计算[14]是一种全新的计算模型, 目前其与智能计算的融合主要有两类模式, 一类是面向量子计算机的纯量子智能计算, 例如量子机器学习[15]、量子支持向量机[16], 运行这类算法需量子硬件支撑, 目前属于超前的理论研究； 另一类是面向经典计算机的量子衍生智能, 如量子遗传算法[17]、量子粒子群算法[18]等, 这类算法是借用量子计算的某些机制(例如量子比特的旋转、翻转和测量)提升传统智能优化算法的性能。笔者提出量子教学优化算法属于第2类, 即通过在基本教学优化算法中引入量子计算机制, 提升其寻优能力, 从而揭示了量子衍生计算模型相比于对应的传统优化模型的优势。笔者详细给出了算法的基本原理、设计方案。以44个不同维度的标准测试函数为优化对象, 通过与基本教学优化算法及其他典型群智能优化算法对比, 全面考察了所提算法的优良性能。仿真结果表明, 在基本教学优化算法中引入量子计算, 以提升其优化性能的研究思路是可行的。

1 教学优化算法

教学优化算法[19]的灵感源于学校班级中, 老师教导学生以及学生相互学习的过程。整个过程中, 学生成绩的提高来源于教师的教学和学生的交流。基本教学优化算法分为两个阶段： 教师阶段和学生阶段。在教学优化算法中, 每个人视为一个个体, 而将老师视为适应度值最好的个体, 将学生所学习的科目视为不同的决策变量, 而学生的成绩视为适应度值。

设个体总数为N, 其中教师个数为1, 学生个数为N-1, 个体向量维度为D, 个体搜索空间为S=RD, 教师与学生种群为X=(X1,X2,…,XN), 初始种群为X(0), 迭代n次后的种群为X(n), 目标函数为f。以极小值优化为例, 教学优化算法可描述为以下两个阶段。

1.1 教学阶段

1) 对每个个体Xi(i=1,2,…,N), 计算出其目标函数值(即成绩), 选择班级成绩最优者为教师。

2) 设Mt为第t步迭代学生的平均水平(成绩),Tt为第t步迭代的教师, 通过将Tt看作全班学生新的均值Mnew, 可获得两个均值之间的差

Di=ri(Mnew-TFMt)

(1)

3) 按下式计算与Xi对应的Xnew,i

Xnew,i=Xi+Di

(2)

4) 若Xnew,i优于Xi, 则置Xi=Xnew,i, 否则Xi保持不变。

1.2 学习阶段

在学习阶段, 学生之间随机选择学习目标。假设学习者Xi随机选择学习者Xj≠i, 函数f(X)表示学生X的水平。Xi通过

(3)

获得新解, 然后采用贪婪选择策略决定是否保留该解。最后, 判断是否满足终止条件, 若满足, 则终止； 若不满足, 则返回至教学阶段第1)步。

2 量子教学优化算法

笔者提出一种量子教学优化算法(QTLBO： Quantum-Teaching-Learning-Based Optimization), 考虑到传统TLBO中, 在教师阶段教师自身不能进化, 在学生阶段缺乏优良个体的引领, 因此将QTLBO的两个核心过程修改为： 1) 教师自学； 2) 向教师学。这样做的好处是, 教师既能通过自学提升自身性能, 又能充当“路标”引领学生进化。

2.1 量子比特相关概念

2.1.1 量子比特的球面描述

量子比特是量子信息的基本单位, 1个量子比特可表示为基态|0〉和|1〉的叠加态, 如下所示

(4)

根据θ和φ的连续性可知, 一个量子比特可以描述无穷多个不同的状态。

2.1.2 量子比特的绕轴旋转

笔者算法在Bloch球面上建立搜索机制, 具体通过量子比特的绕轴旋转实现。采用的两种旋转如下。

1) 绕坐标轴旋转。根据量子计算理论, 量子比特绕3个坐标轴旋转δ弧度的旋转算子分别由以下酉矩阵描述[20]

(5)

(6)

(7)

记量子比特|φ〉=[cosθ/2,eiφsinθ/2]T, 则|φ〉绕3个坐标轴旋转δ弧度的旋转操作可分别写为|φx〉=Rx(δ)|φ〉, |φy〉=Ry(δ)|φ〉, |φz〉=Rz(δ)|φ〉。以绕y轴旋转为例, 具体旋转方法如图1所示。

2) 绕任意轴旋转。记P=[px,py,pz]和Q=[qx,qy,qz]为Bloch球面上任意两点, 根据量子计算原理, 量子比特以最短路径由点P向点Q旋转δ弧度的旋转轴为P和Q的向量积[21], 即Raxis=P×Q, 旋转矩阵可表示为

(8)

具体旋转方法如图2所示。其中I是单位矩阵,σ=[σxσyσz]为按下式定义的泡利矩阵

(9)

图1 量子比特绕y轴的旋转 图2 量子比特绕任意轴的旋转 Fig.1 The rotation of qubit about the y-axis Fig.2 The rotation of qubit about any axis

2.1.3 量子比特的投影测量

对量子比特实施投影测量的目的在于获得量子比特|φ〉的Bloch球面坐标值(x,y,z), 根据量子计算原理, 该过程可通过泡利矩阵实现

值得指出, 与基于单位圆的搜索机制相比, Bloch球面搜索的优点是对解空间的遍历更为精细, 也更能增强种群的多样性(对数值较为接近的两个候选解, 在Bloch球面上的距离可能较大, 从而可增强候选解的多样性), 进而避免早熟收敛； 缺点是计算量较大, 但作为非在线实施的优化问题, 优化精度是首先要考虑的因素, 因此笔者采用在Bloch球面建立搜索机制。实际上Bloch球面搜索是单位圆搜索的推广, 单位圆搜索是Bloch球面搜索的特例。当保持θ=π/2时, Bloch球面搜索即为单位圆搜索。

2.2 QTLBO编码方案

在QTLBO中, 个体采用基于Bloch球面描述的量子比特编码。设种群规模为N, 优化空间为D维, 记第t代种群为P(t)=[p1(t)p2(t) …pN(t)], 则种群初始化时第i个体pi(0)可按

pi(0)=[|φi1(0)〉|φi2(0)〉…|φiD(0)〉]

(13)

编码, 其中i=1,2,…,N。

2.3 解空间变换

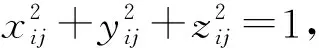
Xij=[Lj(1-xij)+Sj(1+xij)]/2

(14)

其中i=1,2,…,N,j=1,2,…,D。

2.4 教师学习阶段

由于教师是当代种群中的最优个体, 其没有可以参照的“路标”, 因此描述教师的量子个体采用绕着坐标轴旋转的方法产生新的候选解。

由于笔者采用了量子比特的x坐标作为优化解, 而量子比特绕x轴旋转时, 其x坐标不变, 因此采用绕y轴或z轴旋转。具体选择方法： 若|yj|≤|zj|, 则绕y轴旋转; 否则绕z轴旋转; 这样选择的依据是, 可使xj有较大的调整范围。关于旋转角度, 若选取区间过大, 可导致搜索步长过长, 容易错过全局最优解； 而选取区间过小, 则导致搜索步伐过小, 从而降低搜索效率。同时可变的角度区间势必增加算法的控制参数, 从而降低算法的普适性。经过大量重复实验, 将其设置为(-0.1,0.1)弧度之间均匀分布的随机数, 此时对绝大多数优化问题都可获得满意解。

在每步迭代中, 教师的自学次数设为N。即通过使教师个体上的每个量子比特绕着坐标轴旋转, 产生N个新个体, 然后在原教师和旋转产生的N个新个体中选择最优个体, 使其充当学生向教师学习阶段的“路标”。

2.5 向教师学习阶段

该阶段属于有“路标”的向导式学习, 所有N-1个学生个体都向经过自学后的新教师看齐。笔者采用使量子比特绕特定坐标轴旋转的方法实现, 具体方法简述如下。

1) 对第t步迭代的第i个个体pi(t),i=1,2,…,N, 从1,2,…,D中随机选择一维d。

2.6 算法终止条件

在群智能优化算法中, 终止条件一般为两种：精度阈值和迭代步数。精度阈值即当优化结果小于(极小值优化)或大于(极大值优化)给定阈值时, 终止算法运行； 迭代步数即当算法达到限定步数时不论是否满足给定阈值, 都终止算法运行。笔者采用迭代步数作为终止条件。

2.7 算法实现步骤

Step 1 初始化。按式(13)随机生成N个个体组成初始种群, 按目标函数值升序排序, 将第1个(对于极小值优化)或最后1个(对于极大值优化)个体作为教师, 其余N-1个体作为学生。设置迭代步数G, 置当前迭代步数t=0。

Step 2 实施教师自学, 通过使教师比特绕坐标轴旋转, 结合贪婪搜索策略实施教师自身更新, 为下一阶段提供路标。

Step 3 学生向教师学, 在D维搜索空间中随机选择一维, 采用学生比特和对应的教师比特建立旋转轴, 使学生个体向着教师逼近, 计算其目标函数值, 采用贪婪搜索策略实施个体更新。

Step 4 在整个种群的N个个体中选择最优解, 以此作为下一代种群中的教师。

Step 5t=t+1, 若t>G, 保存最优解, 算法终止； 否则转向Step 2。

3 仿真结果及分析

为充分验证QTLBO算法的优越性, 笔者将QTLBO算法与TLBO算法、人工蜂群算法(ABC)、粒子群优化 (PSO)、差分进化算法(DE： Differential Evolution)4种算法进行对比。利用以上5种算法对44个标准测试函数进行极小值优化, 下面首先给出测试函数。

3.1 测试函数

1) 低维函数。根据复杂程度, 16个低维函数(序号为F01～F16)分为如下4类。单峰可分离函数(US： Unimodal Separable)：f01～f02； 单峰不可分离函数(UN： Unimodal Non-Separable)：f03～f06； 多峰可分离函数(MS： Multimodal Separable)：f07～f09； 多峰不可分离函数函数(MN： Multimodal Non-Separable)：f10～f16。各函数解析式如下。

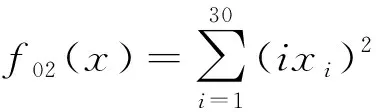
③f03(x)=-cos(x1)cos(x2)exp(-(x1-π)2-(x2-π)2)

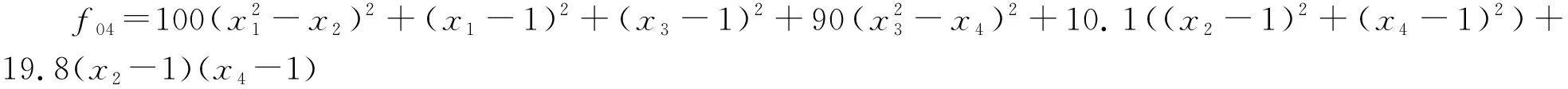
2) 高维函数。28个高维函数均来源于CEC2013中的标准测试函数[22]。其中包含单峰可分离函数(US)：f1,f5, 单峰不可分离函数(UN)：f2～f4, 多峰可分离函数(MS)：f11, 多峰不可分离函数(MN)：f6～f10,f12～f20, 复合可分离函数(CS： Composition Separable)：f22, 复合不可分离函数(CN： Composition Non-Separable)：f21,f23～f28。

3.2 相关参数设置

3.2.1 测试函数参数设置

1) 对28个高维函数, 除第8个函数的变量上限设置为32, 变量下限设置为-32, 其余函数的变量上限均设置为100, 变量下限均设置为-100。仿真中函数维度均取D=50。

2) 对16个低维函数, 根据函数的复杂程度设置不同的变量上下限以及函数维度D, 如表1所示。

表1 16个低维函数变量上下限表

3.2.2 算法参数设置

笔者经过多次仿真, 最终各算法参数设置如下。对种群规模, QTLBO设置为25, TLBO、DE、PSO、ABC均设置为50； 对PSO算法, 其加速常数(c1,c2)均设置为1.496 18, 惯性因子设置为随迭代次数的增加从0.9线性下降到0.4； 对ABC算法, 其探测阈值设置为L=100, 采蜜蜂和跟踪蜂的数目设置为(25,25)。对DE算法, 其缩放因子F设置为随迭代步数从0.2线性增加到0.9, 交叉概率C由当代归一化方差向量确定。TLBO与QTLBO均无特殊的控制参数。为使函数运算结果更加精确, 增强对比结果的客观性, 降低优化结果的随机性, 笔者将QTLBO、TLBO、ABC、PSO、DE 5种算法对每个测试函数均独立运行30次, 通过对比结果平均值评价算法性能。

3.3 仿真结果对比

不同算法的复杂度不同, 计算效率也不同, 若单纯考察相同迭代步数下的性能对比, 显然不够全面。因此, 考察5种对比算法在相同运行时间下的性能对比。关于如何才能保证算法有相同的运行时间, 笔者采用的方法是为各种算法设置依赖于自身复杂度的不同迭代步数, 作为算法的终止条件。关于每种算法迭代步数的具体设置, 根据相同迭代步数下各种算法所需时间的比值决定。例如, 在相同迭代步数下, 算法Alg_1和算法Alg_2的时间对比是k∶1, 若算法Alg_1的迭代步数设置为1 000, 则算法Alg_2的迭代步数可设置为1 000k。

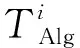
笔者将QTLBO的迭代步数设置为1 000, 根据上述比值, 对16个低维函数, 4种对比算法的迭代步数分别设置： TLBO为2 000, PSO为8 000, DE为6 000, ABC为3 000； 对28个高维函数, 迭代步数分别设置： TLBO为4 000, PSO为10 000, DE为8 000, ABC为5 000。

虽然运行结果能反映算法性能的优劣, 但优化结果还是存在一定的偶然性。为更客观地评价所提算法的性能, 对参与对比的5种算法的优化结果, 笔者采用概率统计理论中的秩和检验方法对其进行性能差异的显著性检验, 从而评价算法性能。

对秩和检验方法, 首先将统计阈值设置为α=0.05, 其原假设H0约定为： “对于同一函数, QTLBO的优化结果和其他算法的优化结果没有差异”。关于检验结果W, 约定W=“+”表示原假设H0被拒绝, 且QTLBO以至少95%的概率优于对比算法；W=“-”表示原假设H0被拒绝, 且QTLBO劣于对比算法。W=“=”表示原假设H0被接受。

将5种算法采用每个函数分别独立运行30次, 对优化结果采用秩和检验进行对比评价。表2给出了16个低维函数的秩和检验结果, 表2中对不同类型函数, 算法显著性结果的分类统计如表3所示。28个高维函数的秩和检验结果和相应的显著性统计结果如表4和表5所示。

从表2和表3可知, 4种类型的低维函数(US,UN,MS,MN)除了单峰变量可分离(US)这类函数, QTLBO与TLBO的优化性能大致相等外, QTLBO算法的优化性能均优于4种对比算法, 且对多峰变量不可分离函数, 相比于对比算法的优势更为明显, 这表明QTLBO对于求解复杂的多峰变量不可分离的优化问题具有较大优势。

从表4和表5可知, 6种类型的高维函数的对比结果展示了与低维函数优化基本相同的趋势。其中对单峰变量不可分离(UN)函数, QTLBO与TLBO大致相当, 但略弱于DE。除此之外, 对其他所有类型函数, QTLBO都优于对比算法。从而表明QTLBO对高维优化问题同样具有优势。

表2 16个低维函数QTLBO与TLBO、PSO、DE、ABC的威尔逊秩和检验结果

表3 16个低维函数QTLBO与TLBO、PSO、DE、ABC的统计结果对比(+/-/=)

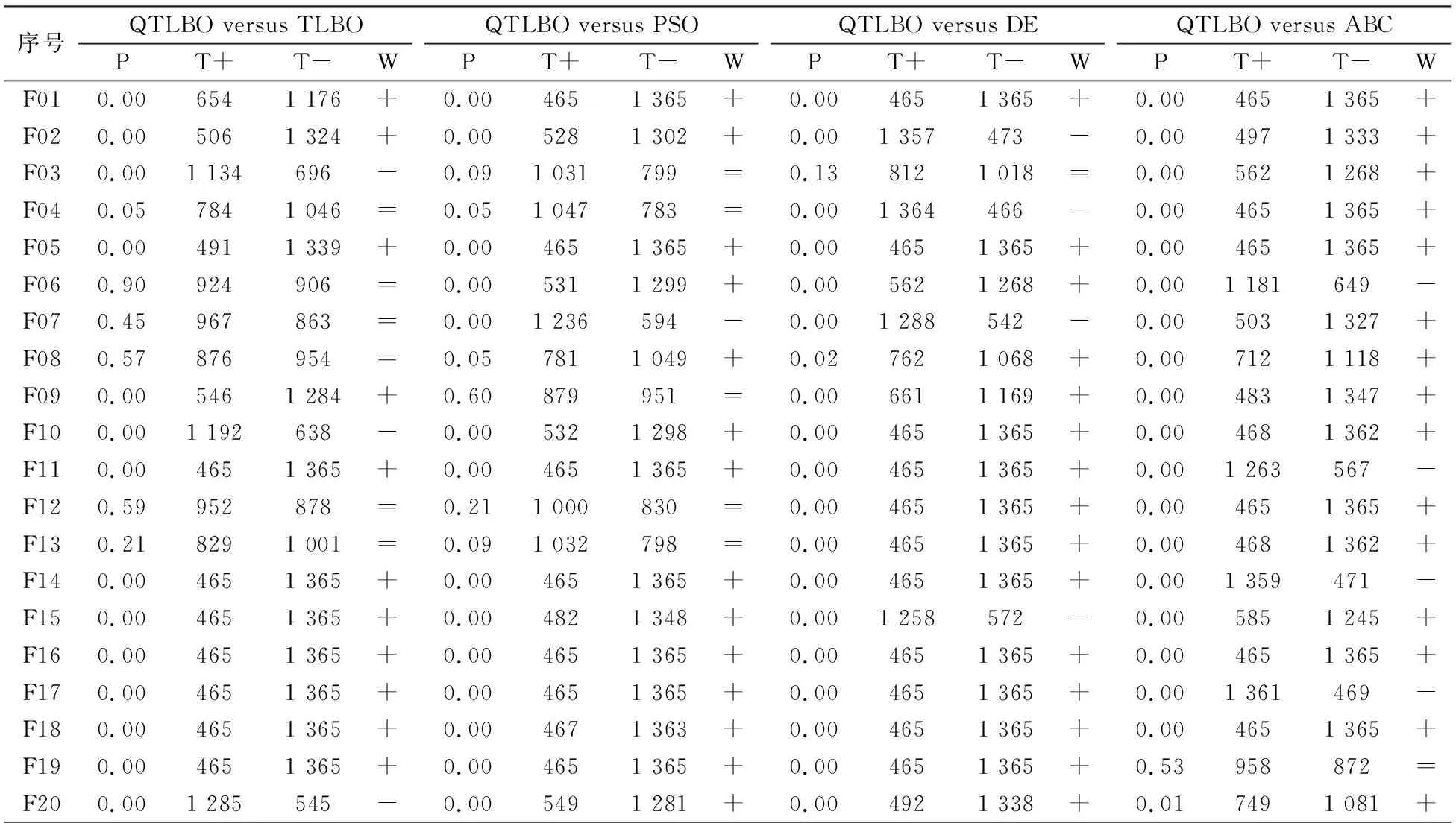
表4 28个高维函数相同运行时间下QTLBO与TLBO、PSO、DE、ABC的威尔逊秩和检验结果

(续表4)

表5 28个高维函数相同运行时间下QTLBO与TLBO、PSO、DE、ABC的统计结果对比(+/-/=)

3.4 仿真结果分析

对上述结果, 给出如下理论分析。

首先, QTLBO优于TLBO在于算法结构的改进。在QTLBO中, 采用“教师自学”和“向教师学”两种机制, 分别取代了TLBO中的“向教师学”和“学生互学”。在TLBO寻优过程的“向教师学”阶段, 教师仅起到“路标的作用”, 引领学生向自己学习, 而自身不再进行任何改进；在“学生互学”阶段, 方向性较差, 使寻优过程偏向随机搜索。而在QTLBO中, 在教师不仅充当“向教师学”的路标, 起到引领寻优方向的作用, 而且通过“教师自学”可以进一步提高自身能力, 以便为更好地引领学生提升整体知识水平, 即候选解质量。

其次, QTLBO优于4种对比算法的原因在于寻优机制的改进。QTLBO采用了量子计算机制, 使在解空间中每一维的寻优过程都在Bloch球面进行, 这种机制不仅使寻优过程更为精细, 而且不受实际解空间大小的影响, 便于制定统一的优化策略, 同时也提升了算法的鲁棒性。

值得指出, 就计算效率而言, QTLBO是5种算法中最低的。这是因为QTLBO采用了量子计算机制, 与其他算法比较, 增加了旋转轴和旋转矩阵的构造、解空间变换等操作。然而正是这些增加的操作使QTLBO的性能得以提升。换句话说, QTLBO是以牺牲计算效率为代价换取优化性能的提升, 然而这种代价是值得的。仿真结果表明, 就相同时间下的优化结果而言, QTLBO仍然好于对比算法。

4 结 语

笔者提出了量子教学优化算法, 通过将基本教学优化算法与量子计算原理融合, 达到了提升教学优化算法优化性能的目的。不同维度标准测试函数在相同运行时间下的优化结果表明, 笔者提出的QTLBO算法与传统教学优化算法以及其他经典群智能优化算法相比, 在复杂函数极值优化方面具有较大优势, 可应用于大规模非线性优化问题。