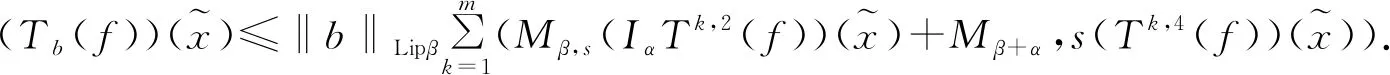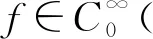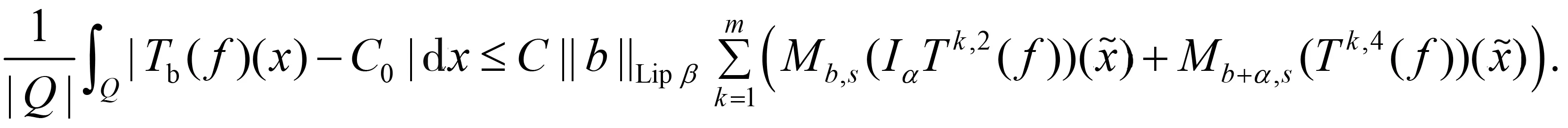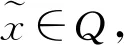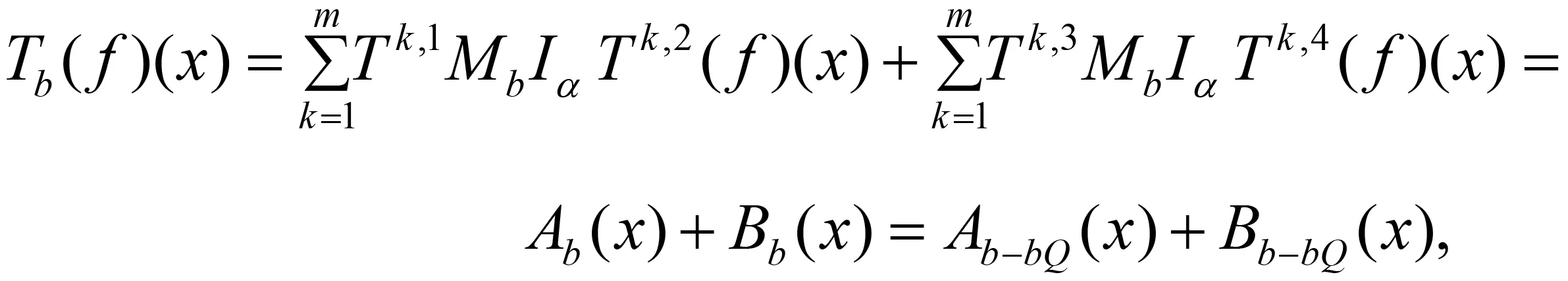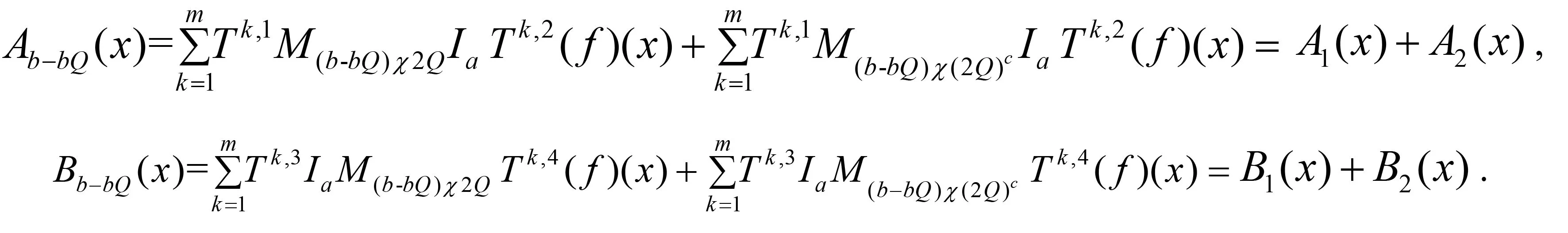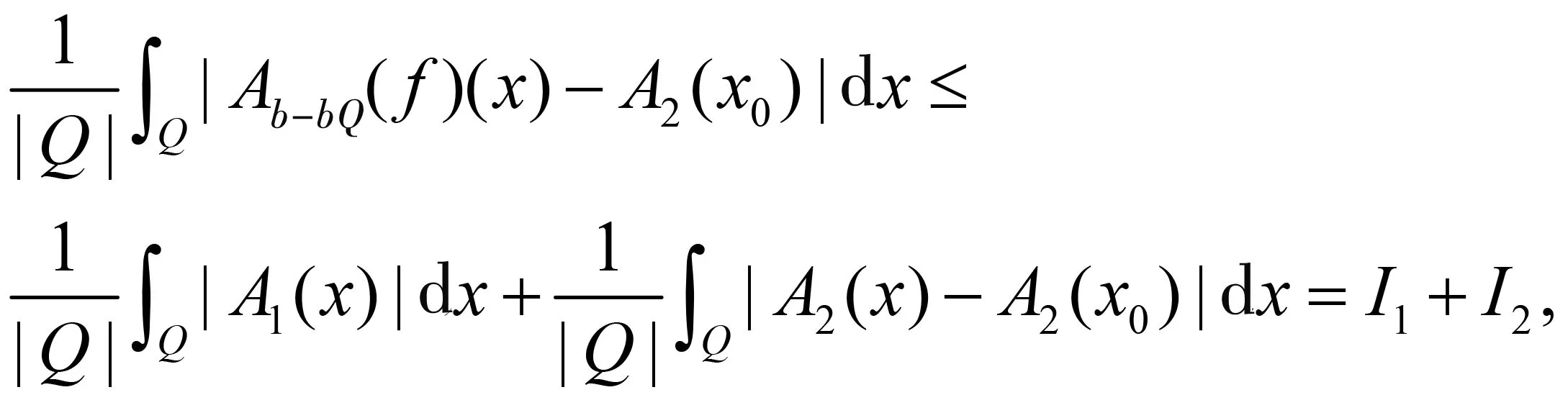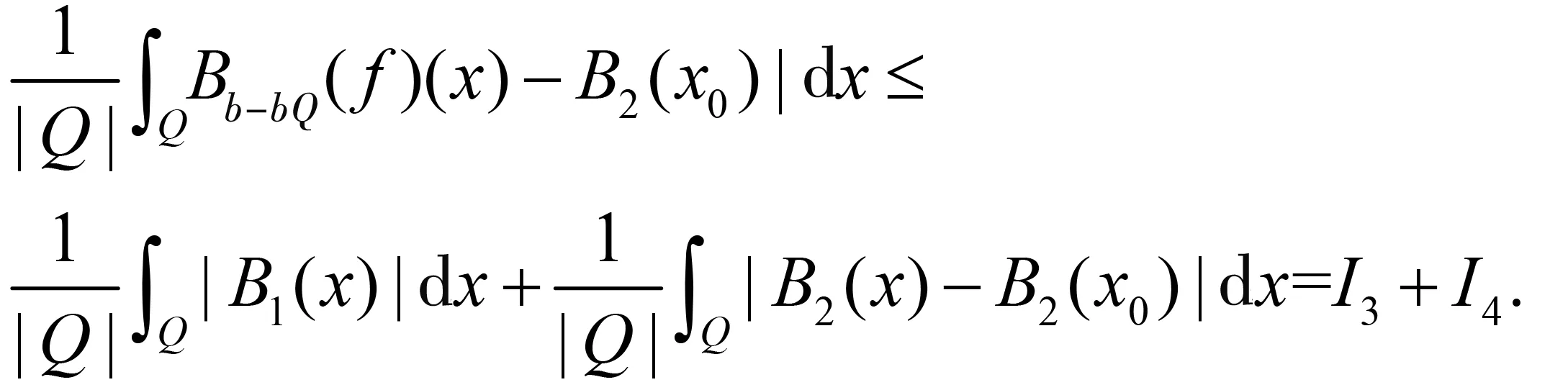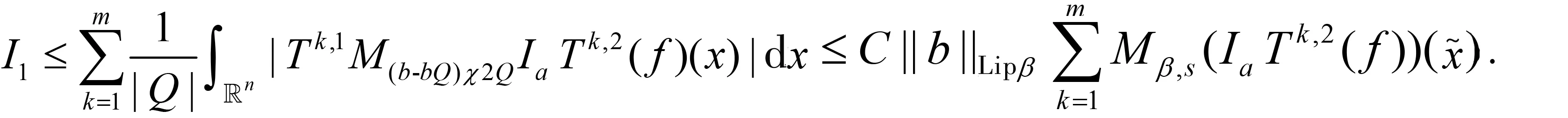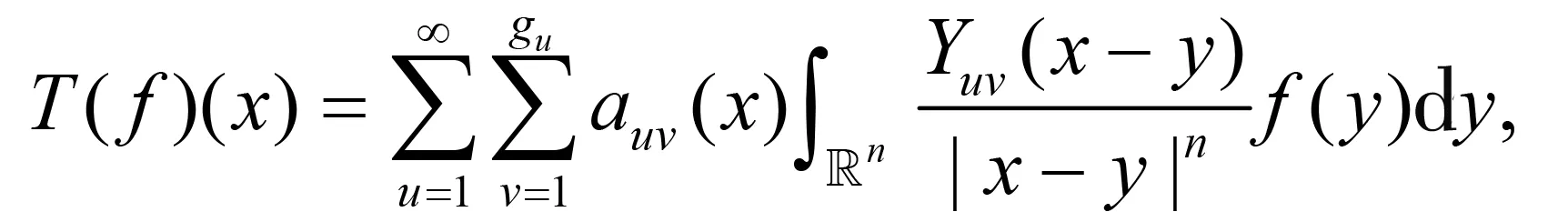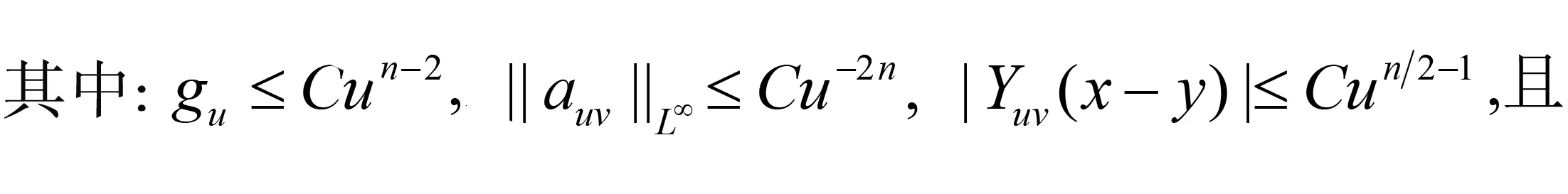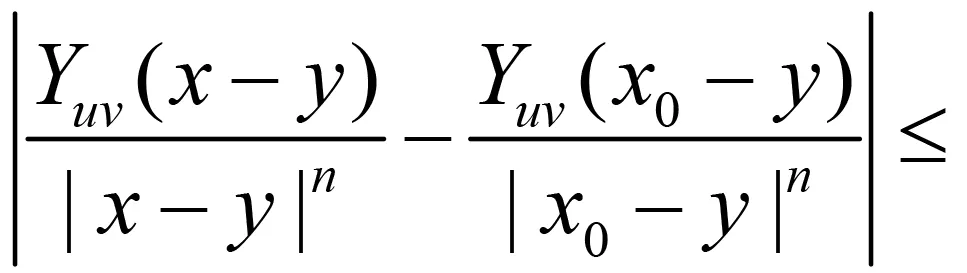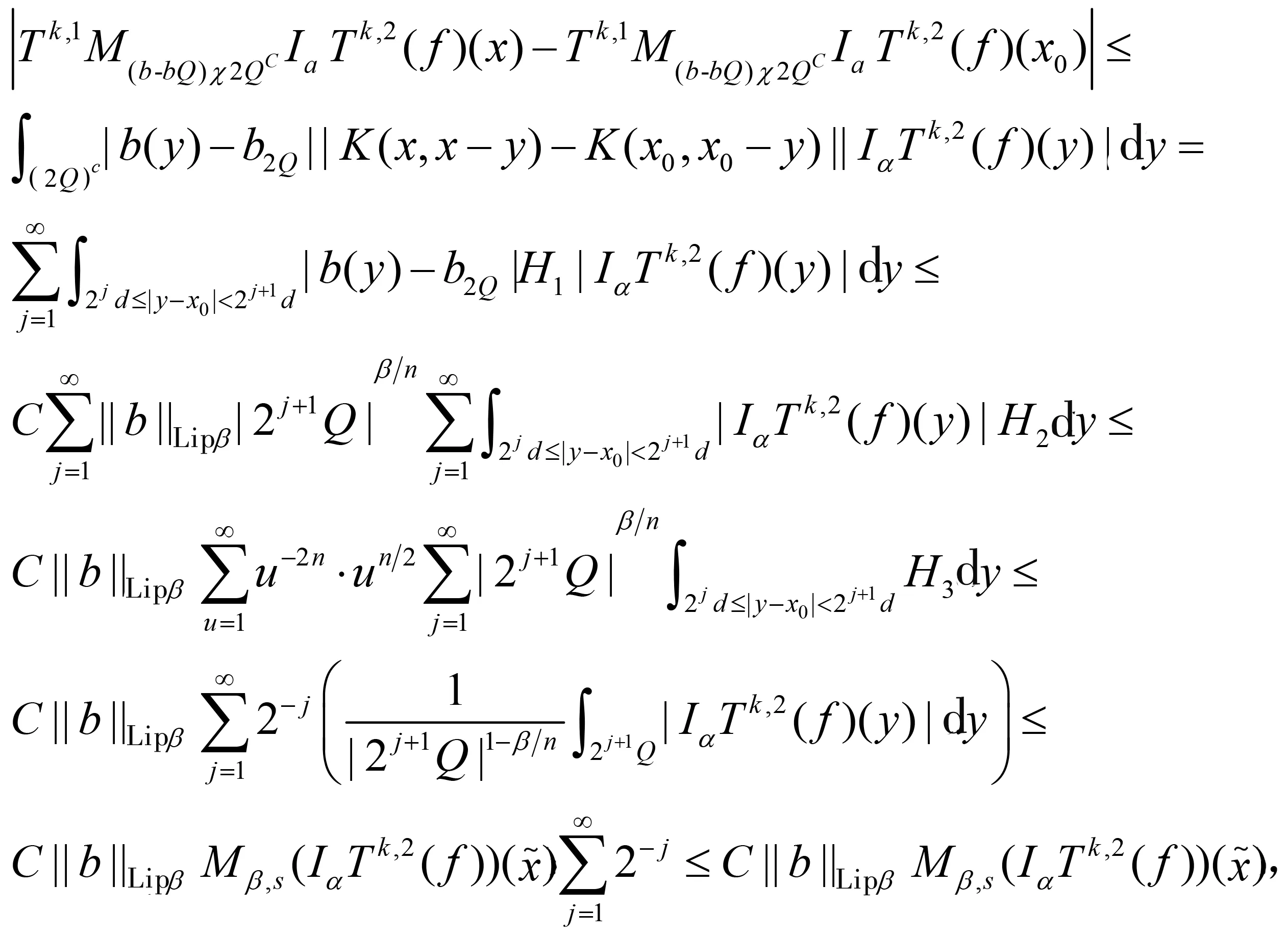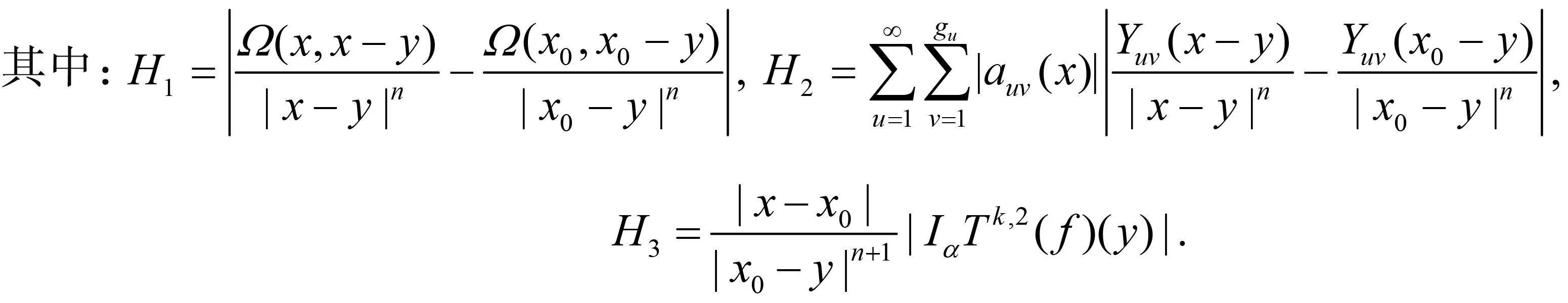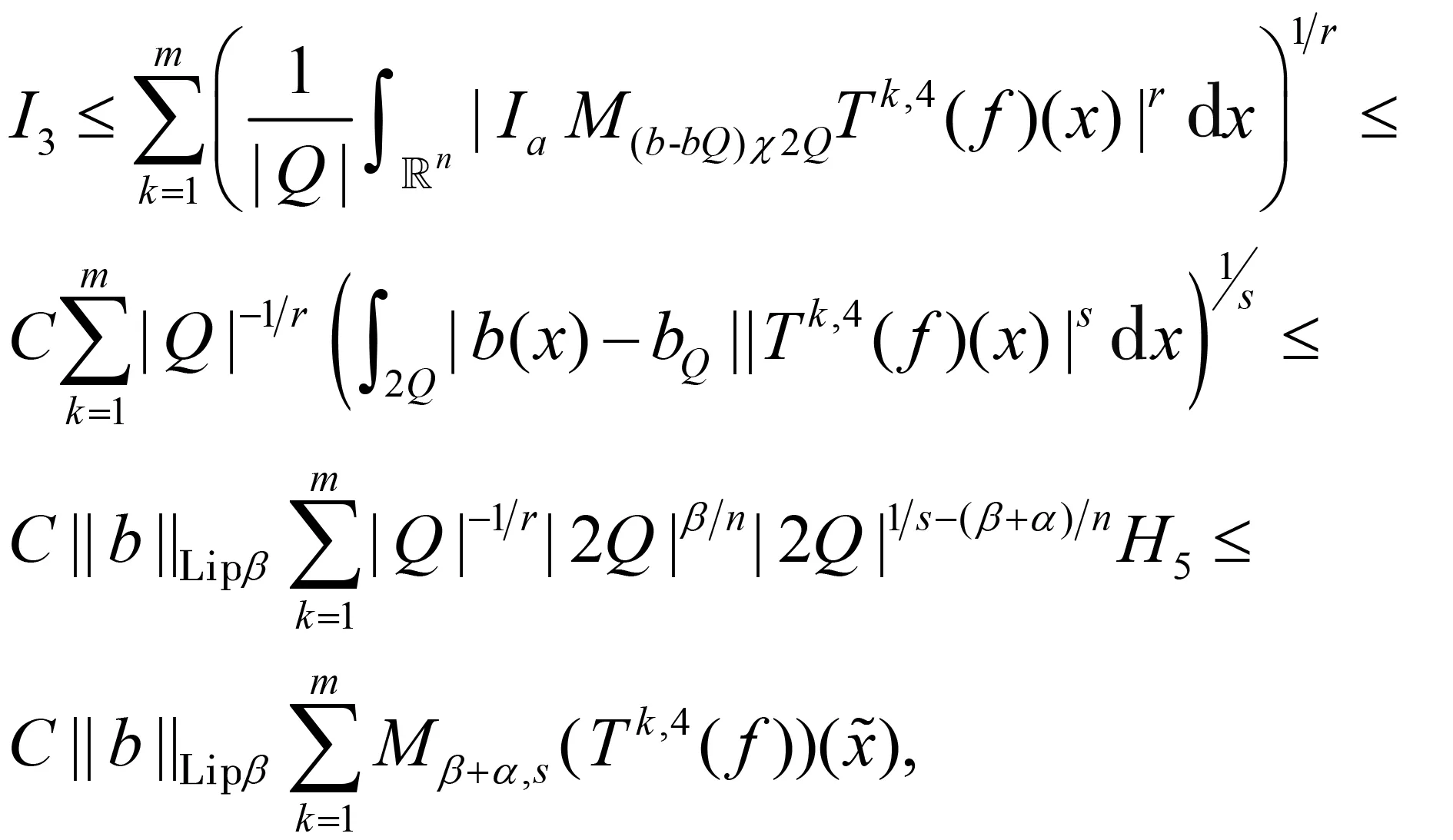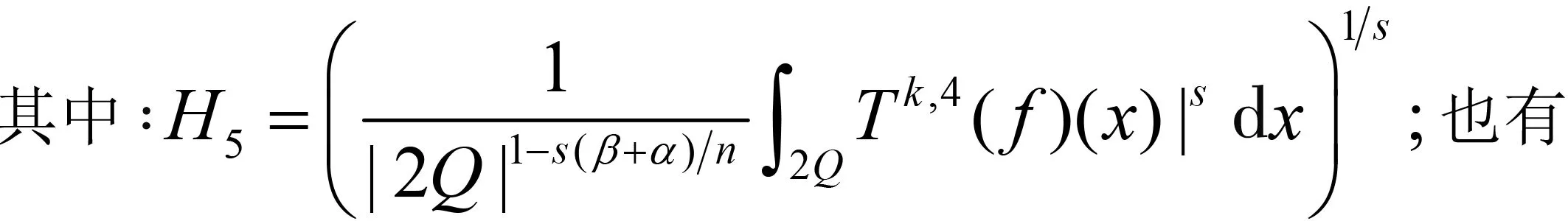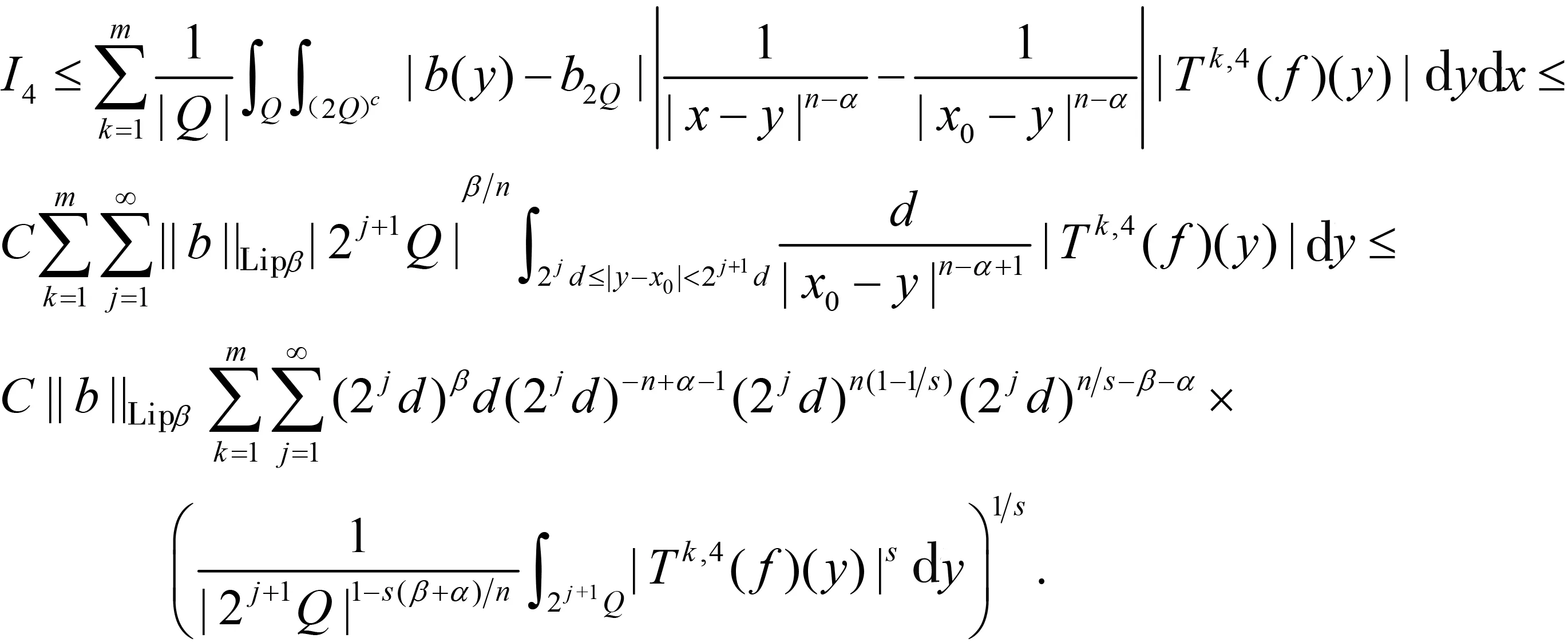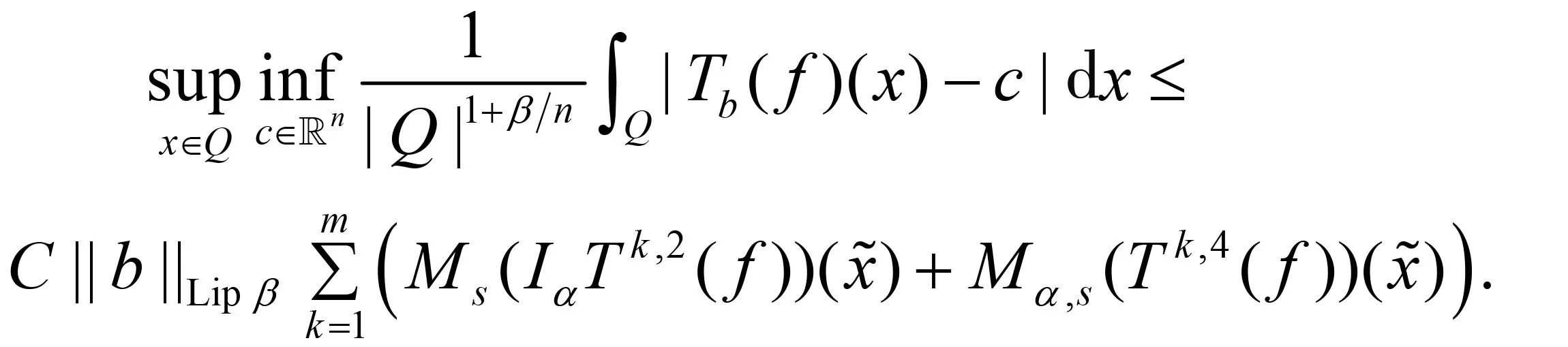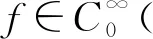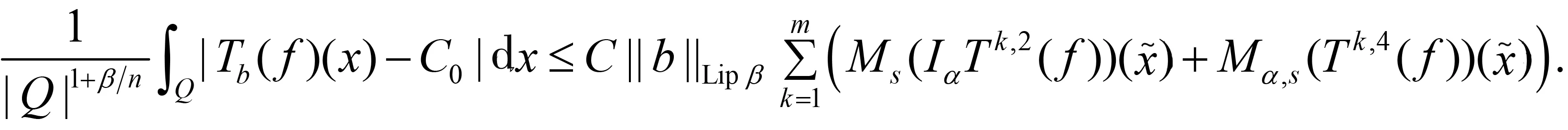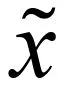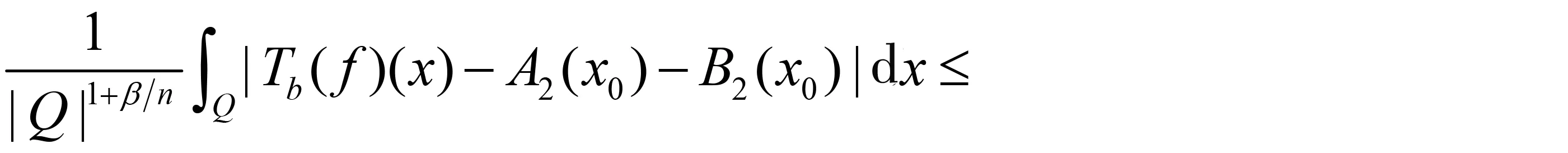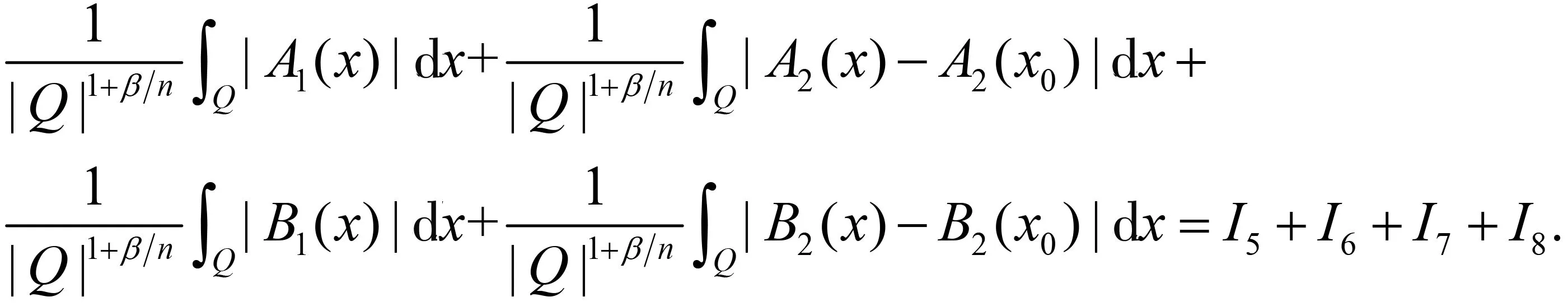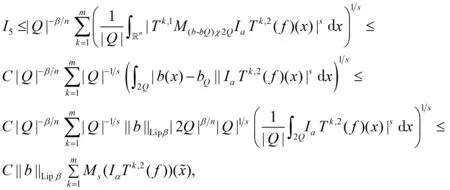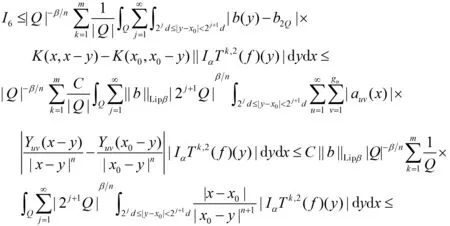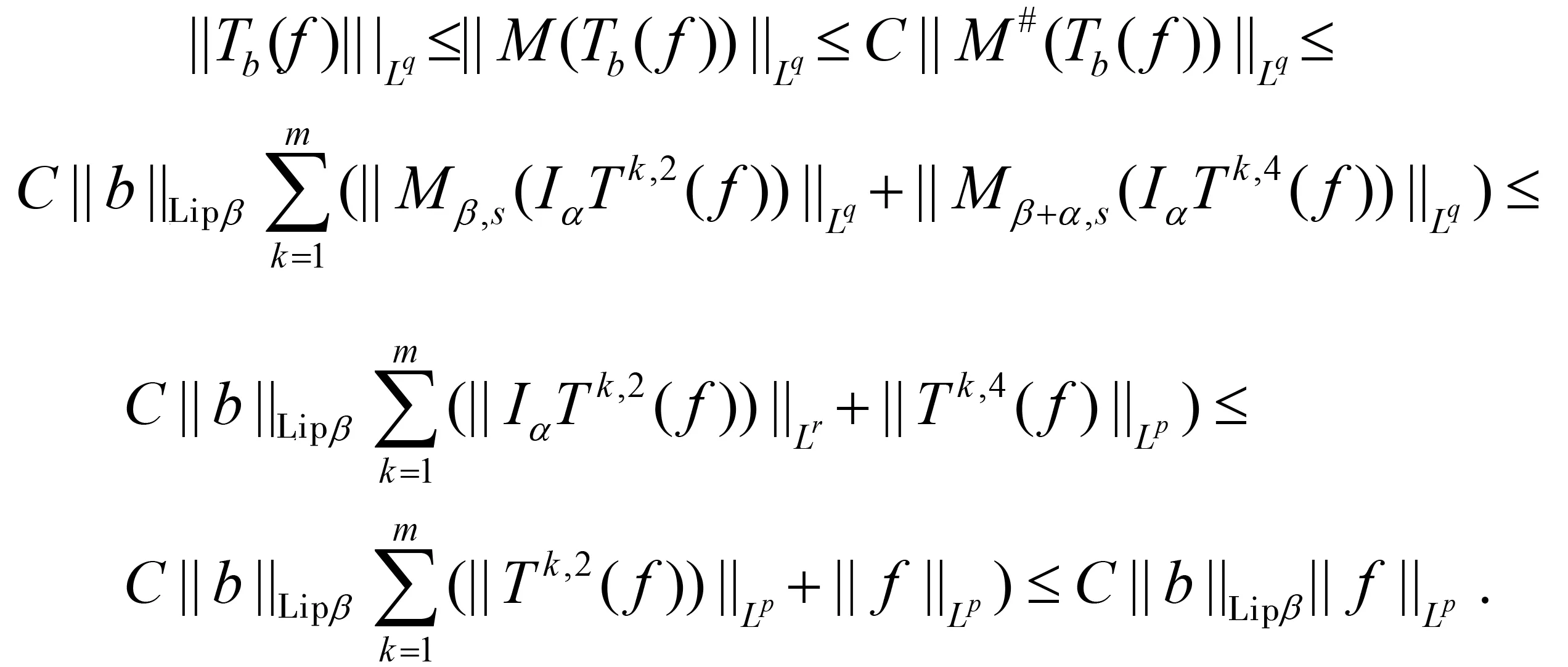带Calderón-Zygmund核的Toeplitz型算子的有界性
赵巧珍 ,黄得建
(1.嘉兴南洋职业技术学院 基础部,浙江 嘉兴 314003;2.海南热带海洋学院 理学院,海南 三亚 572022)
0 引言
随着奇异积分算子的发展[1-2],它们的交换子已经得到了很好的研究.文献[3-5]证明了1 本研究讨论了带Calderón-Zygmund核的奇异积分算子和Lipschitz函数生成的Toeplitz型算子的有界性.为了讨论方便,引入下面定义. 定义[9]222设K(x,y)=Ω(x,y)/|y|n:n×(n/{0})→.K称为可变Calderón-Zygmund核,且满足以下两个条件: (1)K(x,·)是一个Calderón-Zygmund核,x∈n; 设b是n上的局部可积函数,T是带有可变Calderón-Zygmund核的奇异积分算子,其数学表达式为 Toeplitz型算子定义为 其中:算子Tk,1是可变Calderón-Zygmund核的奇异积分算子T或±T(单位算子);算子Tk,2和Tk,4是线性算子,Tk,3=±I(k=1,2,…,m),Mb(f)=bf和Iα是分数积分算子(0<α 为了证明主要结论,本研究引入以下几个引理. 引理1[9]233设T是定义中的奇异积分算子,则T在Lp(n)(1 引理2[8]4对于0<β<1,1 引理3[11]635对于(1 引理4[11]636对于0<α ‖Iα(f)‖Lq≤C‖f‖Lp, ‖Mα,s(f)‖Lq≤C‖f‖Lp. 定理1设T是定义中的奇异积分算子,0<β<1,1 其中: 于是有 对于I1,利用Hölder不等式及引理1,有 因此有 对于I2,由文献[9]的公式4.1[9]230和文献[10]的定理2[10]463可知 Cun/2|x-x0|/|x0-y|n+1. 对于|x-y|>2|x0-x|>0,x∈Q,可得 因此 类似地,由引理4,对于1/r=1/s-a/n,有 定理2设T是定义中的奇异积分算子,0<β<1,1 类似定理1的证明方法,对于1/r=1/s-α/n,有 定理3设T是定义中的奇异积分算子,0<β<1,1 证明在定理1中取1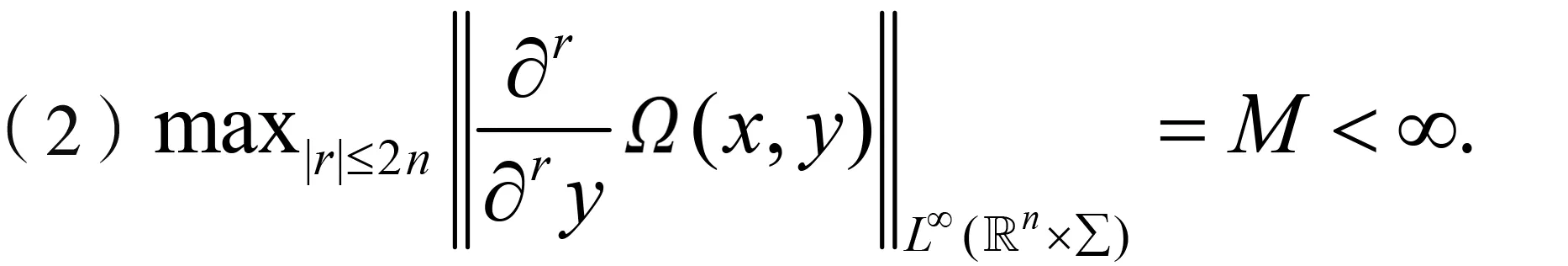

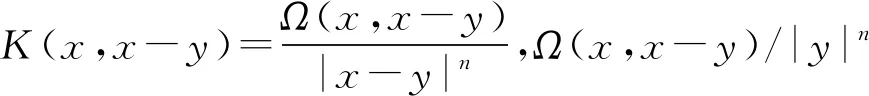
1 引理
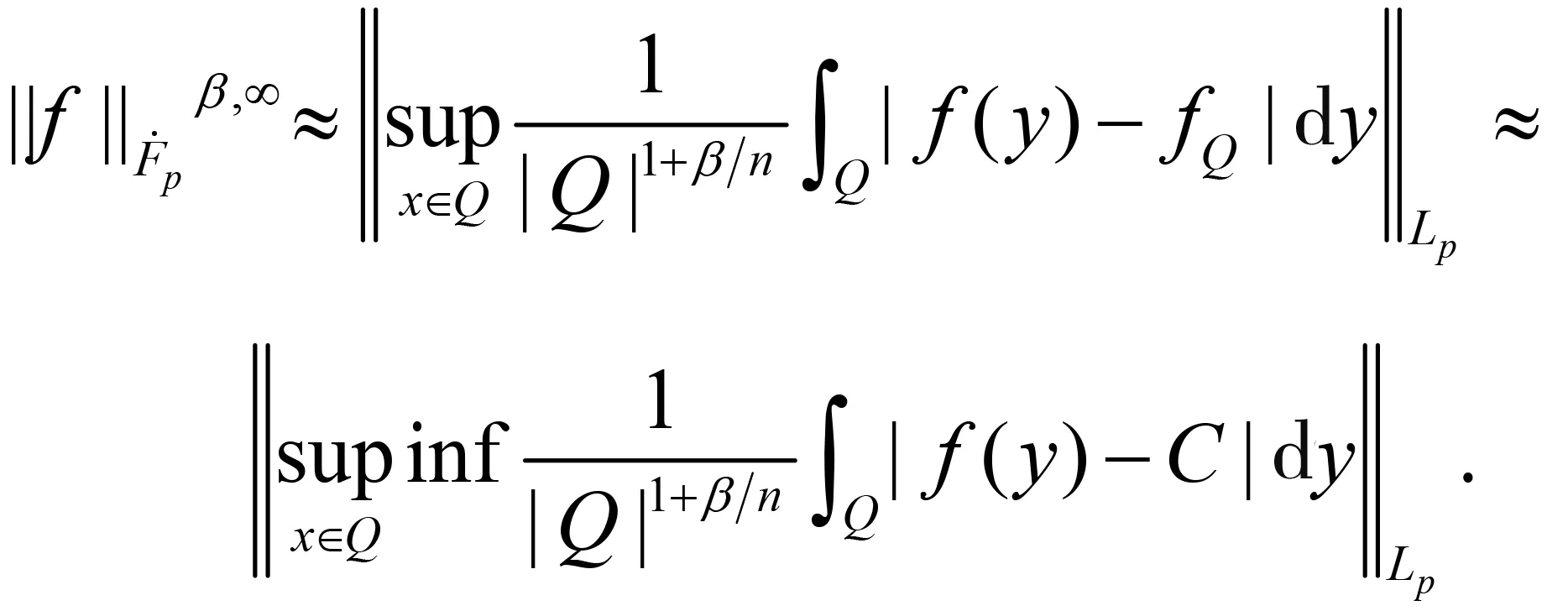
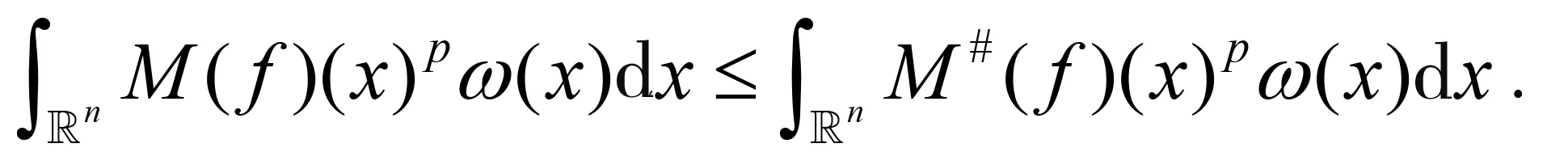
2 定理及其证明