三维空间的Thiessen-多面体及其性质
潘申润,李满枝
(1.福建师范大学 数学与信息学院,福州 350117;2.海南师范大学 数学与统计学院,海口 571158)
0 引言
Thiessen-多边形又称为Voronoi diagram,是由平面中的离散点所形成的三角形外接圆的圆心所形成的多边形.二维平面上Thiessen-多边形与Voronoi diagram所指的是同一类图形,因而长期以来人们习惯性地将Voronoi-多面体也称为Thiessen-多面体[1-4].但是本研究发现Thiessen-多面体与三维Voronoi diagram的形成机理不同,故Thiessen-多面体与Voronoi-多面体的定义与性质均存在不同.
本研究对二维Thiessen-多边形的定义进行拓展,给出Thiessen-多面体新的定义,研究其性质,发现该多面体的体积比原定义的体积更小,即Thiessen-多面体是Voronoi-多面体的改进结果.
1 Thiessen-多面体的提出
本研究将二维平面上的Thiessen-多边形拓展为三维空间下的Thiessen-多面体.
首先,将平面离散点拓展为空间离散点.由于在三维空间中最简单的空间图形为四面体,从而需要保证在中心离散点外存在至少4个外围离散点,对这4个外围离散点要求它们不在一个平面上,且由它们所形成的四面体包含中心离散点.从而本研究可以得到Thiessen-四面体的形成条件,即在Thiessen-多面体的中心离散点周围存在n个外围离散点(n≥4),这n个点不共面、不共球,且由这n个离散点所形成的多面体包含中心离散点.
其次,将三角形拓展为四面体.在Thiessen-多边形形成过程中,将二维平面中的中心离散点与相邻的两个外围离散点互相连接形成一个三角形.而在三维空间中,考虑将平面上的三角形拓展为空间中的四面体,即选取中心离散点为四面体的一个顶点,将相邻的三个外围离散点进行连接形成该四面体的底面.这样依次选取中心离散点外的n个外围离散点构建n个不同四面体的底面,从而形成n个四面体.
再次,将外接圆与外接圆圆心拓展为外接球与外接球球心.在Thiessen-多边形的形成过程中,将中心离散点与外围离散点进行连接形成若干个三角形,之后绘制各个三角形的外接圆并标记圆心位置.在n中圆和球都是紧集,本研究在形成n个四面体的基础上绘制出n个四面体的外接球并标记这n个外接球球心位置,由于要求外围离散点不共面且不共球,从而这个外接球的球心必不重合.
最后,将Thiessen-m多边形拓展为Thiessen-多边形的n个顶点.在Thiessen-多边形的形成过程中,m个外围离散点形成了m个三角形并标记了m个外接圆的圆心,从而形成了一个Thiessen-m边形,即若存在m个外围离散点,则形成的Thiessen-多边形具有m条边.而在Thiessen-多面体的形成过程中,n个外围离散点所形成的n个四面体,可绘制出n个外接球并标记出这个外接球的球心位置,由这个外接球球心所形成的Thiessen-多面体的顶点个数为n.
在对以上内容进行拓展后,得到了一个Thiessen-多面体.
命题1(Thiessen-多面体的形成条件一) 外围离散点所形成的多边形包含中心离散点.
命题1的判定条件有以下两类:一是先确定有可能穿过的包含k个顶点的所有的折线,然后对计算射线所穿透的链的数目进行判定[5];二是通过将多面体的面片和多边形的边组织成层次结构,运用二分查找算法判定[6].
命题2(Thiessen-多面体的形成条件二) 中心离散点与任意四个相邻的外围离散点不共面、不共球,即n个外围离散点所形成n个四面体的n个外接球球心不重合.
命题3(Thiessen-多面体的形成过程) ①选取中心离散点将其与外围3个相邻的离散点进行连接形成一个四面体,从而根据外围离散点的数目n形成n个四面体[图1(a)].②对于四面体按其面是否相邻,依次对面相邻的四面体进行排序.③绘制各个四面体的外接球并标记外接球球心[图1(b)].④依次连接各个外接球球心形成面,生成一个以外接球球心为顶点的多面体O1O2O3O4O5O6[图1(c)].

图1 Thiessen-多面体的形成过程
由图1可知,我们将由命题3所形成的多面体O1O2O3O4O5O6称为Thiessen-多面体,称M为中心离散点,而A,B,C,D,E和F为外围离散点,O1,O2,O3,O4,O5和O6为Thiessen-多面体顶点.
定义1(Thiessen-多面体的新定义) 根据Delaunay三角网形成法则,对M点相邻的n个离散点进行编号,以M为顶点,对于编号相邻的三点形成四面体的底面三角形,形成n个四面体.记Q(n)为这n个四面体外接球球心所组成的点集,则以Q(n)为顶点所形成的多面体称为以M为中心离散点的Thiessen-多面体.
2 Thiessen-多面体的性质
2.1 Thiessen-多面体的顶点、面、棱的性质
为更好地给出Thiessen-多面体顶点、面、棱的性质,先给出关于无效多面体底面、无效多面体与无效多面体面的定义,并给出了多面体欧拉定理作为引理.
定义2由非相邻的外围离散点所形成的四面体底面称为无效四面体底面;由无效四面体底面所形成的四面体称为无效四面体.
定义3由外接球球心组成点集Q(n)的某些元素所形成的一个面Γ,若存在Q(n)中的剩余元素分布在面Γ的两侧,则称面Γ为无效Thiessen-多面体面.
引理1(多面体欧拉定理) 简单多面体的顶点数V、面数F及棱数E间有如下恒等式关系:
V+F-E=2.
①
注:可以考虑通过类比法证明该引理成立[7].
性质1中心离散点与n个外围离散点(n≥4)所形成的Thiessen-多面体具有n个顶点.
证明结合命题1与命题2,可以发现由中心离散点与n个相邻的外围离散点形成了n个四面体,而这n个四面体对应着有n个外接球的球心恰好是点集Q(n)的元素,从而此时所产生的Thiessen-多面体具有n个顶点.
性质2中心离散点与n个外围离散点(n≥4)所形成的Thiessen-多面体最多具有(2n-4)个面,最多具有(3n-6)条棱.

2.2 Thiessen-多面体的凹凸性.
凸多面体是指把多面体的任何一个面伸展成平面,如果所有其他各面都在这个平面的同侧[8-9].
性质3任一Thiessen-多面体是凸多面体.
证明在排除无效多面体面之后,Thiessen-多面体面的个数最多为2n-4,且这(2n-4)个面均可以认定为是引理1中所描述的面ω.由于Thiessen-多面体的特殊形成条件,则任一Thiessen-多面体都是凸多面体.
3 Thiessen-多面体与Voronoi-多面体
3.1 Thiessen-多面体与Voronoi-多面体的定义
定义4(Voronoi-多面体的定义) 中心离散点与其近邻各外围离散点间连线的垂直平分面所围成的[10]、具有最小体积的多面体称为Voronoi-多面体[11].
定义5(Thiessen-多面体的另一定义) 假设V={V1,V2,…Vn}(n≥4)是3空间上的一个点集,并且这些点不共线、不共球.记ω(A,B)为点A,B间的垂直平分面,设P为3空间上的点,从而定义新的一个点集我们将由点集Q(n)为顶点所形成的多面体称为以P为中心离散点的Thiessen-多面体.
相较Thiessen-多面体与Voronoi-多面体的形成过程及定义,我们不难看出其中存在的区别,即Thiessen-多面体的形成在于规则地标记外接球的球心,根据外接球球心所组成的点集Q(n)为多面体顶点所形成的;而Voronoi-多面体则是由出中心离散点与其近邻各外围离散点间连线的垂直平分面所围成的多面体.
3.2 Thiessen-多面体与Voronoi-多面体的图形
为更为直观地展示Thiessen-多面体与Voronoi-多面体的区别,我们将同样条件下单独形成的Voronoi-多面体(图2),它为相同条件下所形成的Voronoi-多面体,它与Thiessen-多面体进行对比(比对情况图3),其中Thiessen-多面体为以中心离散点M与外围离散点A,B,C,D,E,F所形成的多面体.

二者最大的区别在于:Thiessen-多边形存在6个顶点、8个面;Voronoi-多面体存在8个顶点、6个面.可见相同条件下Voronoi-多面体的部分顶点与Thiessen-多面体的顶点和面是重合的.
3.3 Thiessen-多面体与Voronoi-多面体的新理论
由图3能够直观地看出Thiessen-多面体与Voronoi-多面体是两个不同的图形,但两者之间存在着一定的联系.
定理1Thiessen-多面体与Voronoi-多面体是两个不同的图形,当且仅当Thiessen-多面体为锥体时,Thiessen-锥体与Voronoi-锥体是重合的.
证明Thiessen-多面体与Voronoi-多面体是两个不同的图形,其最大的区别在于顶点与面的个数.性质1说明了n个外围离散点(n≥4)所形成的Thiessen-多面体具有n个顶点;而Voronoi-多面体是由中心离散点与其近邻n个外围离散点(n≥4)间连线的垂直平分面所围成的、具有最小体积的多面体,从而Voronoi-多面体具有n个面,这个面是由其n个外围离散点所提供的[12].由此,可以说明当空间一个中心离散点的外围存在n个外围离散点(n≥4)时,所产生的的Thiessen-多面体具有n个顶点,Voronoi-多面体具有n个面,即Thiessen-多面体与Voronoi-多面体是两个不同的图形.但我们也应当注意到,若一个空间图形具有n个顶点与n个面时,此时Thiessen-多面体与Voronoi-多面体重合.由棱锥的性质可以说明了Thiessen-锥体具有n个顶点与n个面,并且这n个面分别是中心离散点与n个外围离散点的垂直平分面,即Thiessen-锥体与Voronoi-锥体是重合的.
定理2Thiessen-多面体可看作若干个平面切割Voronoi-多面体所得出.
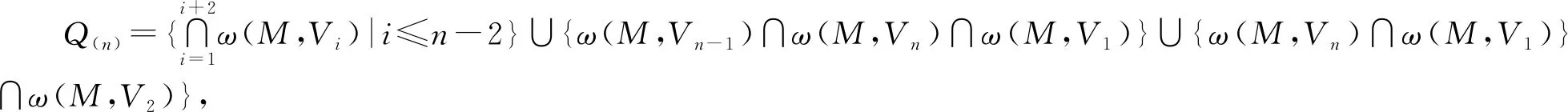
由定理2可以给出Thiessen-多面体的一个新的定义.
定义6(Thiessen-多面体的另一个新定义) 在中心离散点M与外围离散点形成Voronoi-多面体的基础上标记出外接球球心所组成的点集Q(n)中的所有元素,取过Q(n)的3个元素形成一个平面P,使得Q(n)中的剩余(n-3)个元素在该面的同一侧,Voronoi-多面体顶点所组成过的点集R(p)中的元素在该面的另一侧[17],用这样的P对Voronoi-多面体进行切割,剩余的部分为Thiessen-多面体.
定理3由中心离散点与外围离散点所形成的Thiessen-多面体嵌入在相同情况下形成的Voronoi-多面体中.
证明Thiessen-锥体与Voronoi-锥体重合时,此时可以认定Thiessen-锥体嵌入在Voronoi-锥体内.以下考虑非Thiessen-锥体的情况,由定义6可知,Thiessen-多面体可以由同等条件下的Voronoi-多面体通过平面切割的方式得到,Thiessen-多面体是在Voronoi-多面体中通过形成新增侧面所形成,且该侧面为Thiessen-多面体的一个面,它截去了Voronoi-多面体的一个顶点.经过若干次平面的切割后剩余的Voronoi-多面体嵌入在原有Voronoi-多面体中.从而推出由中心离散点与外围离散点所形成的Thiessen-多面体嵌入在相同情况下形成的Voronoi-多面体中.
定理4由中心离散点与外围离散点所形成的Thiessen-多面体的体积与表面积小于等于相同情况下形成的Voronoi-多面体的体积与表面积.


图4 Voronoi-多面体经平面ABC切割后被截去的棱锥D-ABC
对于任一棱锥,底面积恒小于其他面的总和,即SABC≤SDAB+SDBC+SDAC,图中SDAB,SDBC,SDAC为Voronoi-多面体表面积的一部分,经过平面ABC的截取后,面ABC为新增侧面,即此时的Thiessen-多面体的面,从而经过有限次的平面切割之后剩余的部分(Thiessen-多面体)的表面积小于Voronoi-多面体的表面积,即由中心离散点与外围离散点所形成的Thiessen-多面体的体积与表面积小于等于相同情况下形成的Voronoi-多面体的体积与表面积.
至此,我们讨论了Thiessen-多面体与Voronoi-多面体的区别与联系,并得到了几个重要的结论,也证明了Voronoi-多面体的体积并非最小,Thiessen-多面体是同等条件下形成的最小体积的多面体.为后续改进与优化现有利用Voronoi-多面体构造的数学模型[18-19]提供理论依据.
5 结论
本文主要介绍了一个全新的概念——Thiessen-多面体.一组空间的中心离散点与其相邻的三个外围离散点形成四面体,其外接球球心作为顶点构造出Thiessen-多面体.
根据这个新定义,推导了Thiessen-多面体的性质:①若Thiessen-多面体的顶点数为n,则最大的面数为2(n-2),最大的棱数为3(n-2);②Thiessen-多面体是凸多面体.
通过比较Thiessen-多面体与Voronoi-多面体的定义与性质,得到了几个结论:①提出并证明了Thiessen-多面体与Voronoi-多面体是两类不同的图形;②改进了Voronoi-多面体的一些理论,提出了在同等条件下体积最小图形的构造过程;③Thiessen-多面体可看作若干个平面切割Voronoi-多面体所得出;④Thiessen-多面体是嵌入在Voronoi-多面体中.这些新的理论与定理都将为进一步推导出Thiessen-多面体的新应用提供理论依据.
这些研究工作还值得进一步拓展,具体可以考虑以下几个方面:
1)推导Thiessen-多面体的更多性质.对Thiessen-多面体的其他性质做进一步补充和完善;
2)Thiessen-多面体的应用.在后续的研究中将重点研究根据Thiessen-多面体的性质,建立相应的数学模型以解决空间分割或计算体积等问题;
3)将Thiessen-多面体由三维拓展至更高维.三维空间下的Thiessen-多面体是由二维平面中的Thiessen-多面体拓展而得出的.从而可以考虑将空间维度进一步拓展至更高维度,以研究在高维空间下所形成Thiessen-空间体及其性质,因此将得到一系列新的概念与性质,并利用这些新理念解决社会生活中的实际问题.
——三角形一个共线点命题的空间移植

