基于非奇异终端滑模技术的DC-DC Buck变换器研究
郑则炯,黄 鹏,程晓燕
(1.广东轻工职业技术学院 机电技术学院,广东 广州 510300;2.日立电梯(中国)有限公司 技术研发部,广东 广州 511430)
1 研究背景
目前,DC-DC Buck变换器已在不同行业(如汽车新能源等)中陆续使用,其稳定性和响应快速性将决定它的使用寿命。所以,对DC-DC Buck变换器稳定性及动态性的深层次研究具有现实意义[1-2]。目前,国内外许多学者对DC-DC Buck变换器控制策略进行了研究,其中常见的非线性控制方法有:平均电流技术[3-4]、传统滑模技术[5-6]及终端滑模技术[7-10]等。
在平均电流技术方面,文献[3]提出了一种对平均电流进行改进的控制方法,其控制原理简单,但该方法的难点是要对2个补偿器进行设计及参数整定。文献[4]针对DC-DC Buck变换器的瞬态响应,提出了一种基于遗传算法控制平均电流的方法,但该方法相当复杂且稳定性较低。
在传统滑模技术方面,文献[5]采用传统比例积分控制器(proportional integral controller,PI)与滑模控制相结合的方法,即采用传统PI 技术对外环电压进行控制,同时采用滑模控制技术对内环电流进行控制,但该方法存在工作频率不固定、动态响应慢的缺点;文献[6]采用线性化反馈进行固频滑模控制,该方法的优点是具有快速的瞬态响应,不足的是稳态误差较大。
上述2种技术方法只有当时间趋向无限时,状态变量才无限趋近于稳定点,而终端滑模技术能使状态变量在有限时间内快速收敛于稳定点。例如文献[7]设计了一种有限时间终端滑模控制器,文献[8]提出了DC-DC Buck变换器电压-电流双闭环终端滑模控制方法。二者均采用指数趋近律来设计控制律,从而使DC-DC Buck变换器电压输出有快速的收敛,但因为符号函数不连续而导致输出控制量存在奇异性及不连续性,这会使变换器高频地震抖。又如文献[9]中所述的终端滑模控制器、文献[10]中所提的DC-DC Buck变换器滑模控制系统未建模动态诱发谐波分析方法,二者均能在有限时间内使DC-DC Buck变换器电压输出误差收敛到稳定点,但其不足在于收敛上限时间值会受初始状态变量值的影响,从而导致收敛上限时间值存在误差。
因此,针对在DC-DC Buck变换器中采用平均电流技术设计的系统补偿器较为复杂,及传统滑模技术中存在工作频率不固定、响应速度较慢的难点,本文将以脉冲宽度调制(pulse width modulation,PWM)为契机,进行非奇异终端滑模控制的研究,对开关器件占空比与控制变量进行等效控制。
2 DC-DC Buck变换器数学模型
DC-DC Buck变换器的电路拓扑图如图1所示。图中VIN表示直流输入电压,R表示负载,DC-DC Buck变换器处在CCM(continuous conduction mode)工作模式下,将系统的状态变量选定为电感电流iL和电容电压VC,开关管具有导通(VT=1)及关断(VT=0)状态,二极管电压VD。

图1 DC-DC Buck 电路图Fig.1 DC-DC Buck circuit diagram
当VT=1,即开关管导通时,负载R的电压将由直流电压VIN经过电感L分压后提供,而电容C也将进行充电,其数学方程为

当VT=0,即开关管关断时,负载R的电压将由电容C提供,而电感L将通过二极管续流,其数学方程为
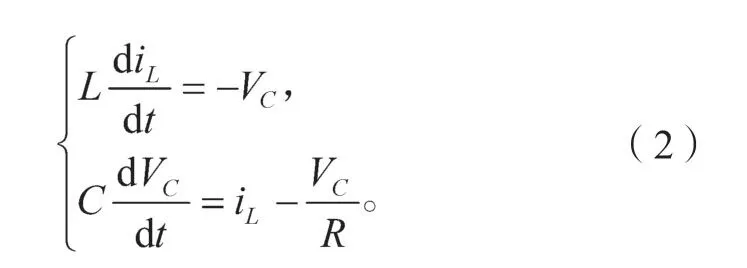
当DC-DC Buck变换器工作在CCM 下时,假设x1=iL,x2=VC,通过状态空间建立相应的空间方程为

式中µ为控制量。
3 非奇异终端滑模技术
3.1 利用双曲正切函数改善指数趋近律
为使DC-DC Buck变换器输出电压保持恒定,可以用DC-DC Buck变换器按输出电压误差及其微分的非线性组合构成,来确定非奇异终端滑模切换面函数。因此,定义输出电压误差

式中xΔ为输出电压参考值。
假设误差变量为e2,则

由式(3)~(5)得到以e1和e2两个误差为状态变量的状态方程为
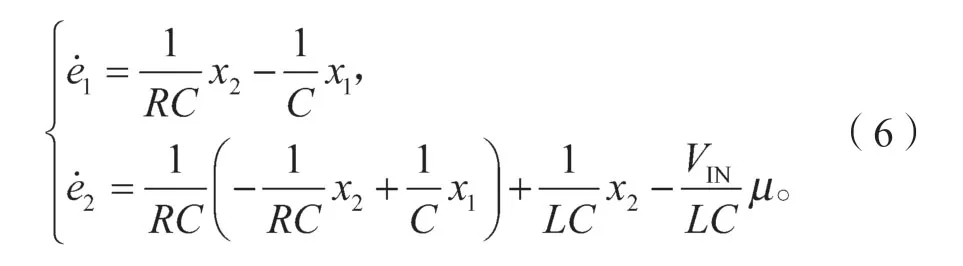
根据输出电压误差与其微分的非线性进行组合设计出切换面函数,即

式中:α为常数,且α>0;
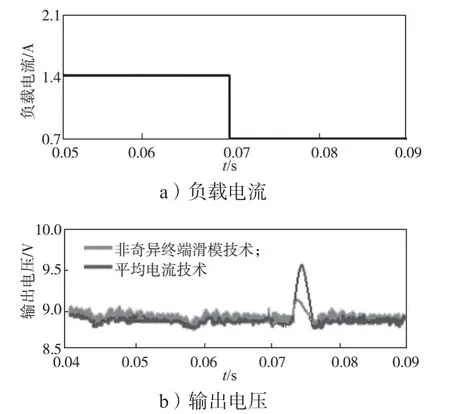
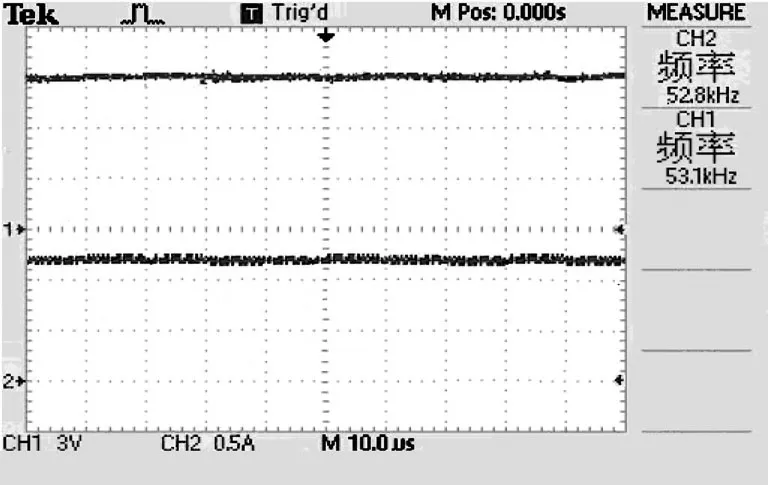
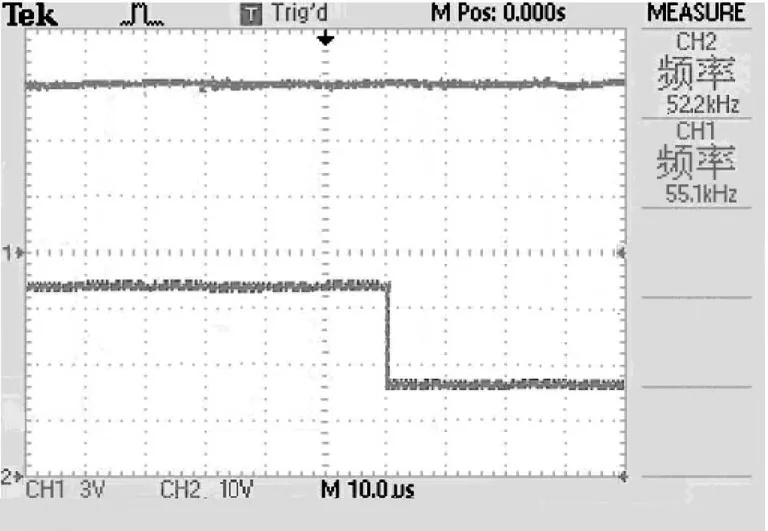
m、n是正奇数,且m 对S(x)求导数,并由式(6)可得 在滑模技术中,因为控制量μ是一种不连续状态,即取0或1[11],滑模技术的运用会导致开关频率不固定。因此,对DC-DC Buck变换器非连续控制量与占空比联系起来,建立等效方式[12]。 设计控制系统时,要求在有限时间里每个状态都要接近切换面。如果按指数趋近律设计控制律[13],其符号函数会呈现不连续现象,得出的设计控制量函数同样会不连续。为了使输出的控制量连续,本文以双曲正切函数来改善指数趋近律的设计[14],即 由式(8)和式(9)可解得所求控制量μ,但计算难度较大,因此在确保趋近律正确的前提下对μ进行简化[15],则有 下面分析所设计非奇异终端滑模技术系统的稳定性。 将式(10)代入式(8)可得 式中α>0, 将式(10)代入式(6)可得 因此,当S>0时,则<0,e2单调递减;当S<0时,则>0,e2单调递增;当=0时,将实现有限时间里使S=0。 通过Matlab Simulink 软件对搭建的DC-DC Buck变换器电路,进行本文所设计的非奇异终端滑模控制仿真研究,并与平均电流控制的情形进行对比,以检验当输入电压发生变化或负载电流发生变化时,非奇异终端滑模技术的响应速度及其稳定性。表1是DC-DC Buck变换器电路的相关参数,图2是非奇异终端滑模技术控制原理图。控制的基本思路是:将非奇异终端滑模控制量与PWM 锯齿波相比较,得出开关管VT控制信号,而锯齿波信号将控制开关管的开关频率fs,以保证开关频率的固定。 表1 Buck变换器参数Table1 Buck converter parameters 图2 非奇异终端滑模控制原理图Fig.2 Schematic diagram of nonsingular terminal sliding mode control 图3是DC-DC Buck变换器运用非奇异终端滑模技术后,输出电压与电感电流的仿真波形。由图可知,仿真过程中输出电压、电感电流均无超调量,且输出电压在短时间内快速递增并与参考电压(9 V)接近,而电感电流快速递减接近于1.2 A。 图3 输出电压和电感电流仿真图Fig.3 Simulation diagram of output voltage and inductance current 图4是系统空间状态e1和e2的轨迹仿真曲线。由图可知,两状态变量曲线分别趋近于0,并在0 位置上下波动。图中e1状态变量曲线波动范围较小,可知输出电压的误差将接近于0。 图4 e1和e2 空间状态轨迹仿真图Fig.4 Simulation diagram of e1 and e2 space state trajectory 图5是切换面函数S的仿真曲线。由图可知,函数S将快速趋近于0,并按一定的开关频率在滑模面周围来回振荡。 图6是输入电压出现阶跃突变时,变换器的输出电压仿真波形。由图可知,当t= 0.07 s时,输入电压从 36 V 阶跃降成18 V,当t=0.13 s时,输入电压从18 V阶跃升成36 V,呈规律变化。在整个输入电压发生阶跃突变的过程中,变换器输出电压基本为9 V。 图7是当负载电流发生阶跃突变时,变换器的输出电压仿真波形。由图可知,当t=0.07 s时,负载电流从1.4 A 阶跃降为0.7 A,当t=0.13 s时,负载电流从0.7 A 阶跃升成1.4 A,呈规律变化。在整个负载电流发生阶跃突变的过程中,变换器电压输出始终也保持在9 V 左右。 图5 切换面函数S 仿真图Fig.5 Simulation diagram of switching surface function S 图6 输入电压阶跃突变时变换器输出电压仿真图Fig.6 Output voltage simulation diagram of converter with input voltage step mutation 图7 负载电流阶跃突变时变换器输出电压仿真图Fig.7 Simulation diagram of output voltage of converter with load current step mutation 通过与平均电流技术方法比较,以验证非奇异终端滑模技术的稳定性。当输入电压发生阶跃突变时,变换器输出电压仿真波形如图8所示。由图可知,当t=0.07 s,输入电压从36 V 阶跃降成18 V时,运用平均电流技术输出电压有0.1 V的误差,而运用非奇异终端滑模技术输出电压基本保持为9 V。可见本文的非奇异终端滑模技术抗干扰能力比平均电流技术好。 图8 输入电压阶跃突变时变换器输出电压仿真结果对比Fig.8 Simulation results comparison of output voltage of converter with input voltage step mutation 当负载电流发生阶跃突变时,变换器输出电压仿真波形如图9所示。 图9 负载电流阶跃突变时变换器输出电压仿真结果对比Fig.9 Simulation results comparison of output voltage of converter with load current step mutation 由图9可知,当t=0.07 s,负载电流由1.4 A 阶跃降成0.7 A时,运用平均电流技术方法,输出电压有0.6 V的超调量,而运用非奇异终端滑模技术方法,输出电压的超调量只有0.3 V。可见运用非奇异终端滑模技术比平均电流技术,输出电压自适应调整快。 为进一步验证非奇异终端滑模技术比平均电流技术好,对非奇异终端滑模技术进行实验,如图10所示。实验的主要设备包括Buck变换器、dSPACE实时控制器、直流电源、电压传感器及示波器。实验时,Buck变换器相关参数如表1所示;与控制器参数及控制信号相关的变量文件由系统RTI 产生,通过Control Desk 进行访问;RTI 将完成Matlab Simulink仿真后生成dSPACE 实时控制器硬件系统所需机器代码的下载任务;系统采样时间设为20 μs。 图10 非奇异终端滑模技术实验平台Fig.10 Experimental platform of nonsingular terminal sliding mode technology 实验连接图如图11所示。Buck变换器所选低压功率MOS 管为SSM3K131TU,其工作原理是:通过Matlab Simulink系统控制dSPACE 实时控制器提供PWM 控制信号,然后去控制Buck 拓扑电路中低压功率MOS 管SSM3K131TU;再由电压传感器采样电压输出信号反馈回给Matlab Simulink系统进行误差分析,实现非奇异终端滑模技术控制。整个电路搭线简单直观。 图11 非奇异终端滑模技术实验连接图Fig.11 Experimental connection diagram of nonsingular terminal sliding modetechnology 实验的输出电压与电感电流波形如图12所示。由图12可知,电压输出接近于参考电压9 V,而电感电流接近于1.2 A,均无超调量。 图12 非奇异终端滑模技术输出电压与电感电流实验波形Fig.12 Experimental waveforms of output voltage and inductance current of nonsingular terminal sliding mode technology 当输入电压由36 V 阶跃降成18 V时,分别以平均电流技术与非奇异终端滑模技术进行实验,变换器输出电压波形见图13~14。由图可知,瞬时动态响应测试波形与前面的仿真验证基本一致。因输入电压的变化,运用平均电流技术的变换器,输出电压约产生1 V的误差;而运用非奇异终端滑模技术的变换器,输出电压基本保持为9 V,其抗干扰性较好。 图13 输入电压发生变化时平均电流技术输出电压实验波形Fig.13 Output voltage experimental waveforms of average current technology when input voltage changes 图14 输入电压发生变化时非奇异终端滑模技术输出电压实验波形Fig.14 Output voltage experimental waveforms of nonsingular terminal sliding mode technology when input voltage changes 当负载电流由1.4 A 阶跃降成0.7 A时,同样以平均电流技术与非奇异终端滑模技术分别实验,变换器输出电压的波形分别如图15和图16所示。由图15和图16可知,所测波形与前面的仿真波形也基本一致。因负载电流突然变小,运用平均电流技术的变换器,输出电压有0.6 V的超调量;而运用非奇异终端滑模技术的变换器,输出电压超调量只有0.3 V,其自适应调整较快。 图15 负载电流发生变化时平均电流技术输出电压波形Fig.15 Output voltage waveforms of average current technology under load current changes 图16 负载电流发生变化时非奇异终端滑模技术输出电压波形Fig.16 Output voltage waveforms of nonsingular terminal sliding mode technology when load current changes 非奇异终端滑模技术作为一种非线性控制方法,在输入或输出发生改变时DC-DC Buck变换器具有快速收敛性。这与平均电流技术方法的仿真及实验波形相比较,效果很明显。当输入电压由36 V 阶跃降至18 V时,采用平均电流技术的变换器输出电压的压降远高于非奇异终端滑模技术的;当负载电流由1.4 A 阶跃降至0.7 A时,采用平均电流技术的变换器输出电压有0.6 V的超调量,而非奇异终端滑模技术的只有0.3 V的超调量。可见,非奇异终端滑模技术对系统的动态调节具有很强的响应性及稳定性。


3.2 验证非奇异终端滑模技术的稳定性




4 仿真验证


4.1 非奇异终端滑模技术的稳定性检验

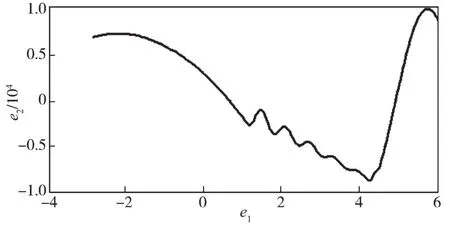



4.2 两种技术的稳定性比较
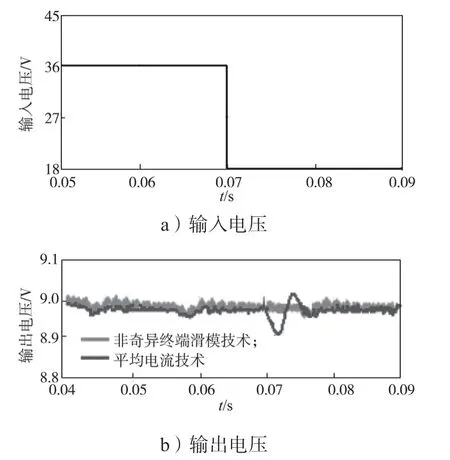
5 实验验证





6 结语

