高效保密的参数区间估计*

陈明艳, 成 雯, 窦家维

1. 陕西师范大学 数学与信息科学学院, 西安710062

2. 陕西师范大学 计算机科学学院, 西安710062

1 引言

随着信息时代的来临, 信息的隐私保护越来越成为人们所关注的问题. 同时人们希望合作对双方甚至多方的信息进行分析计算, 但是实际中拥有数据的各方参与者在计算中并不想泄露自己的数据, 那么如何针对各方的隐私数据合作进行保密判计算成为一个重要的问题. 由于这些隐私保护需要的推动, 安全多方计算(Secure multiparty computation, SMC) 已发展成一个重要的研究方向, 并且成为解决隐私保护问题的重要方法和有力工具[1-5]. 安全多方计算问题是解决两个或多个互不信任的参与者之间为保护隐私而进行的协同计算, 计算结束后, 参与计算的各方除了得到他们设定的计算结果外, 不能获取其他参与方所拥有的隐私数据的任何信息.

姚期智教授在文献[6] 中首次提出两方安全计算问题, 随后Ben-Or 和Goldwasser[7]提出了多方安全计算问题, Goldwasser[8]曾预言安全多方计算将成为计算科学中必不可少的组成部分. 经过众多学者多年来的潜心研究, 目前安全多方保密计算已经形成了较为完整的理论体系, 针对各种实际应用问题研究设计简单高效的保密计算协议大大推动了安全多方计算研究的发展. 安全多方计算在隐私数据的计算、电子商务、保密拍卖、保密存储、计算外包、保密远程访问、入侵检测等方向都有着广泛且重要的应用, 具体可归结为下面几大类: (1) 保密的科学计算[9-11]; (2) 保密的统计分析[12,13]; (3) 保密的几何计算[14-16];(4) 保密的数据挖掘[17]; (5) 保密的数据库查询[18,19]; (6) 其他安全多方计算问题.

随着时代与技术的发展, 多数人都想依靠更精准的数据来使自己的利益最大化, 同时不想泄露自己的隐私. 由于在数据众多的情况下无法做到统计所有的数据, 因而无法得到完全准确的数据结果. 根据统计学的知识, 在数据总体巨大时, 我们可以选取一定数量的样本数据, 通过分析样本数据, 由样本统计量来构造总体参数的估计区间, 这个区间称为参数的置信区间. 置信区间的保密判定在保密的网络波动判断, 保密的患病数据预测, 实际的市场交易中有重要的应用. 例如: (1) 一个公司想要保密的检测另一个公司的产品参数方差是否满足自己的要求. 为不泄露对产品参数方差的要求程度, 保密选取置信度1-α, 判定此参数方差的置信区间是否含于自己的区间中. (2) 两个公司生产同一类产品, 其中一个公司想要保密检测自己公司的产品与另一家公司产品参数均值的差异, 并不泄露产品数据. 则需要保密计算产品参数均值差的置信区间是否含于自己的区间中, 来观察两家产品数据的差异. 为解决类似的参数估计保密判定问题, 本文提出并研究了单个正态总体, 两个正态总体的区间估计保密判定问题.

在统计学中, 参数估计分为点估计和区间估计, 点估计常用的方法包括矩估计、极大似然估计等[20].文献[21] 分别以水平型分布数据和垂直型分布数据为条件设计了保密的极大似然估计协议, 研究解决了有关点估计的保密计算问题. 据我们所知, 区间估计目前还没有很好的研究成果. 本文主要研究参数区间估计的保密判定问题, 计算单个正态总体下方差, 两个正态总体下均值差的置信区间, 结合Paillier 加密算法、Lifted ElGamal 门限加密算法, 得到置信区间端点的密文, 并保密判定此置信区间是否含于一个一方参与者已知的区间. 在已有的研究成果中, 点与区间以及区间与区间位置关系的判定都是在已知明文下进行保密计算的. 文献[22] 首次提出了区间的保密计算, 将区间保密计算问题转化成有限集合包含问题. 文献[23] 利用二叉树中的一个(固定大小的) 节点集来表示整数点和区间, 根据两个节点集的交集显示整数点是否在区间内, 来判定整数点与区间的关系, 提高了计算效率. 文献[24] 根据函数的单调性结合Paillier加密算法, 将离散点与离散整数区间位置关系的保密判定扩展到实数点与连续的实数区间位置关系的保密判定. 文献[25] 利用密码学以及同态加密的相关知识, 设计了从两个明文区间的重叠中选择一个随机的子区间的隐私保护协议并将其应用于物物交换. 由此可见, 保密地判定明文点与明文区间, 明文区间之间关系的研究已经有比较丰富的成果, 但是目前对密文区间与明文区间位置关系的保密判定研究成果还较少,同时在统计分析中针对参数区间估计的保密计算问题还没有好的研究成果. 因此, 针对这一研究现状以及实际应用的需要, 本文研究设计了参数区间估计问题的保密判定协议.

本文主要贡献如下:

(1) 提出并研究了保密统计分析中的新问题, 即参数区间估计的保密判定问题. 拓展了保密统计分析的研究内容.

(2) 提出判定密文区间与明文区间位置关系的解决方案. 通过添加随机数的方法, 将保密判定密文区间与明文区间的位置关系转化成保密判定数据相等问题, 首次解决了密文区间与明文区间位置关系的保密判定问题.

(3) 结合Paillier 加密算法, Lifted ElGamal 门限加密算法, 通过密文区间与明文区间的保密判定, 设计了单个正态总体参数区间估计, 两个正态总体参数区间估计的保密判定协议. 并对协议的安全性和正确性进行了严格证明.

本文第2 节介绍了协议设计中需要用到的预备知识; 第3、4 节设计了具体的协议解决单个正态总体参数区间估计, 两个正态总体参数区间估计问题, 并对其进行了正确性以及安全性分析; 第5 节对本文协议进行了效率分析; 第6 节对全文进行了总结.

2 预备知识

2.1 半诚实模型及其安全性定义

一个半诚实参与者[26]应严格按照协议的要求执行协议, 但有可能会保存在协议执行过程中所得到的信息, 试图在执行协议后推导计算出其他参与者隐私数据的额外信息. 若在协议中所有参与者全部为半诚实参与者, 称这样的模型为半诚实模型.

设f(x1,x2) = (f1(x1,x2),f2(x1,x2)) 是一个概率多项式时间函数, π 是计算函数f 的双方协议. 对于i=1,2, 参与者Pi的输入为xi, 在执行协议中Pi得到的信息序列记作

如果需要证明一个两方计算协议在半诚实模型下是安全的, 就必须构造出满足式(1) 和式(2) 的模拟器S1与S2. 本文所有协议是在半诚实模型下设计的安全计算协议.

2.2 Paillier 加密方案

加法同态性Paillier 加密方案具有加法同态性, 即有下面性质成立: 假设

则有

进一步还可得到Paillier 加密方案的下述乘法性质

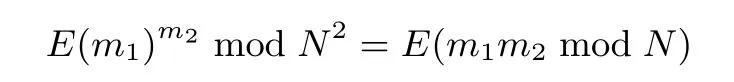
在Paillier 加密方案中, 若选取g = 1+kN(k 为正整数), 则E(m) = (1+kN)mrNmod N2=(1+mkN)rNmod N2. 此时, 加密一个明文m 时, 需要1 次模指数运算; 在解密密文c 时, 由于解密运算中的gλ可以重复使用, 因此解密一个密文也仅需要1 次模指数运算. 下文中都将g 选定为1+kN 的形式.

2.3 Lifted ElGamal 门限加密方案

在门限密码体制中, n 个参与者联合生成公钥, 参与者共同分享私钥. 所有参与者都可以用公钥加密消息, 但解密时必须由t 个(1 ＜t ＜n) 参与者合作才能完成, 少于t 个人联合都无法解密任何消息, 这样的门限密码称为(t,n) 门限. 为保证数据的安全性, 抵抗n-1 个参与者的合谋攻击, 在一般的门限密码体制中, 参与者会选择构造(n,n) 门限.

Lifted ElGamal 门限加密算法的产生是基于ElGamal[28]加密算法, 对ElGamal 算法中明文m 进行处理, 用gm替换m. 下面详细说明Lifted ElGamal 门限加密方案的构造过程.

密钥生成给定安全参数λ, 密钥生成算法生成一个λ 比特的大素数p 以及的一个生成元g. 每个参与者Pi随机选取ki∈作为私钥, 并计算hi=mod p. 公钥为:

加密为加密明文m, 选择随机数r, 按照下式计算密文c:

解密对于密文c=(c1,c2), 每个参与者Pi按照下式解密:

2.4 参数区间估计

在统计学中, 参数估计分为点估计(Point estimation) 和区间估计(Interval estimate). 区间估计是在点估计的基础上, 给出总体参数一个估计的区间范围, 该区间通常通过样本统计量与估计误差结合运算得到. 与点估计不同的是, 在进行区间估计时, 根据所测量的样本统计量不同的抽样分布可以要求一个样本统计量与总体参数的接近程度的概率. 一般地, 利用样本的置信区间(Confidence interval) 对这个样本的总体参数进行区间估计. 置信区间展现的是被估计参数的真实值在一定概率情况下落在所测量结果周围的程度. 它给出的是被测参数通过计算得到的测量值的可信程度, 即为前面所要求的“概率”, 这个概率被称作置信水平. 常见的置信区间分为单个正态总体的置信区间, 两个正态总体的置信区间, 本文分别对这两个问题进行保密的参数区间估计.

对于单个正态总体的参数区间估计, 本文以总体方差为例, 在总体均值未知的情况下, 判断总体方差的置信区间是否含于另一个已知的区间中. 设(x1,x2,··· ,xn) 为取自总体N(μ,σ2) 的样本, 样本方差为s2. 均值μ 未知情况下, 方差σ2置信区间为:

3 单个正态总体的参数区间估计

3.1 问题描述及计算原理

3.2 单个正态总体的参数区间估计保密判定协议

协议1 单个正态总体的参数区间估计保密判定协议

(4) Bob 选择随机数r*, 计算X =(E(t)E(l+4)-1)r*, 并将X 发送给Alice.

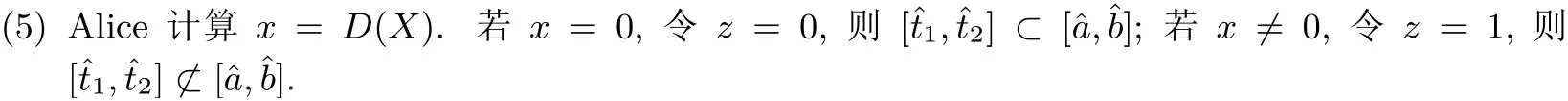
3.3 协议的正确性

3.4 协议的安全性

定理1 协议1 在半诚实模型下是安全的.

证明: 通过构造满足式(1) 和式(2) 成立的模拟器S1,S2证明定理1, 首先构造S1.

令

因此, 协议1 在半诚实模型下是安全的.

4 两个正态总体的参数区间估计

4.1 问题描述及计算原理

4.2 两个正态总体的参数区间估计保密判定协议

4.3 协议2 的正确性与安全性分析

正确性分析

安全性分析

定理2 协议2 在半诚实模型下是安全的.

5 效率分析

在统计学中, 参数估计分为点估计和区间估计, 点估计常用的方法包括矩估计、极大似然估计等. 文献[21] 主要研究了点估计保密计算有关问题, 分别以水平型分布数据和垂直型分布数据为条件设计了保密计算极大似然估计协议. 本文研究了参数估计的另一个方向, 即参数区间估计, 据我们所知, 目前还未见到关于参数区间估计的研究结果. 本文主要研究设计包括单个正态总体、两个正态总体参数区间估计的保密判定协议. 本文与文献[21] 同属参数估计研究方向, 但研究的问题完全不同, 因此无法将本文结果与文献[21] 进行比较. 下面, 我们对本文所设计的两个关于参数区间估计保密判定协议进行效率分析.

通信复杂度本文应用协议所需要的通信次数来衡量通信复杂性.

在协议1 中, Alice 给Bob 共发送3 次信息, Bob 给Alice 发送2 次信息, 所以协议1 通信次数为5次.

在协议2 中, Alice 给Bob 共发送5 次信息, Bob 给Alice 发送3 次信息, 所以协议2 通信次数为8次.

协议效率实验测试 为了进一步分析协议的效率和方案的实际可行性, 本部分通过模拟实验来测试本文协议具体执行中所用的时间. 本文所做的模拟实验均在下面的实验环境中进行.

实验环境 Windows 10 64 位操作系统, 处理器参数为Intel(R) Core(TM)i5-4590s CPU@3.00GHz,4GB 内存. 用Java 语言在Eclipse 上运行实现, 本文所有模拟实验均在此环境下进行. 本文协议1 利用Paillier 加密系统进行模拟, 协议2 利用Lifted ElGamal 门限加密系统进行模拟, 且都忽略预处理时间.由于Alice 与Bob 所做工作有很大不同, 本文分别对两方参与者分别进行实验(见表1).

表1 协议实验效率分析Table 1 analysis on experimental eきciency

6 结论

本文提出了新的多方保密计算问题, 即参数区间估计保密计算. 首先, 根据Paillier 加密算法设计了单个正态总体的参数区间估计保密计算协议. 在此协议中我们同时解决密文区间与明文区间的位置关系保密判定问题, 通过添加随机数的方式, 将密文区间与明文区间的位置关系的保密判定转化为保密判定数据相等问题. 进一步结合Lifted ElGamal 门限加密算法, 设计了两个正态总体的参数区间估计问题, 并证明了协议的安全性. 在后续的研究工作中, 我们将进一步研究恶意模型下有关参数估计的安全计算问题.