基于Rotation-XOR 的MDS 线性变换的研究*

张 晶, 王 鑫, 张丽娜, 杨 波, 胡冰洁

陕西师范大学计算机科学学院, 西安710119

1 引言

Shannon[1]提出密码系统设计的两个基本原则: 混淆和扩散, 分别在迭代型分组密码的混淆层和扩散层具有广泛应用. 混淆层采用非线性的并置S 盒构造. 扩散层采用有限域(Fm2)n上的线性变换构造, 其中m 表示一个S 盒的比特长度, n 表示S 盒的个数. 性能良好的扩散层可抵抗差分密码分析[2]和线性密码分析[3], 其性能通过分支数的大小来衡量, 其中分支数指任意连续两轮运算间最小的活跃S 盒数目.分支数达到最大的扩散层为最优扩散层, 即MDS (Maximum Distance Separable) 扩散层, 其本质是一个MDS 线性变换, 它对应的矩阵为MDS 矩阵, 其中最大分支数为S 盒的数目加1.

MDS 矩阵被广泛应用于各种分组密码算法的设计中, 例如AES[4]、SMS4[5]、Twofish[6]、FOX[7]、流密码算法MUGI[8]、散列函数Maelstrom[9]以及PHOTON 轻量级散列函数族[10]等. 目前构造MDS矩阵主要方法有[11]: 线性码[4]、特殊矩阵[12-19]、线性反馈移位寄存器[9,10,20-22](Linear Feedback Shift Register, LFSR)、循环移位和异或运算[23-27](Rotational-XOR) 等. 其中, 利用线性码、特殊矩阵构造的MDS 矩阵硬件实现效率较低, 因此不适用于资源受限的环境; 基于LFSR 构造MDS 矩阵可节省内存空间, 但需要大量时钟周期, 因此不适用于低时延环境. 基于Rotational-XOR 构造的MDS 线性变换同时具备利用线性码、特殊矩阵和LFSR 构造的优势, 并能增强密码算法抵抗各种密码分析的能力, 故已被很多对称密码算法采用, 例如SMS4 算法、3GPP LTE 国际加密标准ZUC 算法、MD6、SHA-256 等.

2007 年, Wang[23]提出一个基于Rotational-XOR 构造MDS 线性变换的必要条件: 异或项数大于等于n+1, 线性变换中有n 项移位的区间固定; 给出一个构造分块规模为4 的MDS 线性变换的通式.2012 年, 李瑞林、熊海等人[24]研究了基于Rotational-XOR 的对合线性变换, 给出这类线性变换的计数公式, 指出它们的分支数上界为4. 同年, 曹云飞和刘瑶[25]提出一类基于Rotational-XOR、分组规模为32 的MDS 线性变换的构造方法. 2017 年, 郭等人[26]首次在没有辅助搜索的前提下构造出分块规模为4 的MDS 线性变换, 并指出其对应的MDS 矩阵需满足的必要条件, 利用该条件筛选出此规模下MDS线性变换的可能形式. 2018 年, 董新峰等人[27]提出一类基于Rotational-XOR 的轻量化MDS 线性变换的最简形式和构造方法, 并给出分组规模为16 时该类MDS 线性变换的计数结果和相应实例. 然而, 以上文献的研究主要集中在分组规模为16 和32、分块规模为4 的情况, 所得通式也不适用于更大规模. 基于Rotational-XOR 且具有时延低、运算快、计算资源小等特性, 研究更大规模下的MDS 线性变换将缩短数据加解密所用的时间, 使信息传输更加高效.

本文在文献[23,26] 的基础上研究分组规模为64、分块规模为8 的MDS 线性变换的必要条件, 探寻该规模下的MDS 线性变换. 首先通过分析首行矩阵的性质, 给出MDS 矩阵的一个必要条件为矩阵中不可能有连续三个矩阵块相同, 根据该条件证明此规模下异或项数取最小值9 项时不存在MDS 线性变换,并利用Magma 软件验证该结论. 进而研究异或项数为11 项时的MDS 线性变换, 将此情况下的所有线性变换分为三种情况, 分别是一个矩阵中至多有一个自由项、存在两个自由项落在同一矩阵中和三个自由项恰好落在同一矩阵中. 这三种情况将该规模下的88×56×55×54 个线性变换等价划分为15 种形式,设计15 个算法分别搜索后得到此规模下异或项数取11 项时也不存在MDS 线性变换.

2 预备知识

2.1 基本符号

2.2 分支数

定义1 L 的差分分支数定义为:

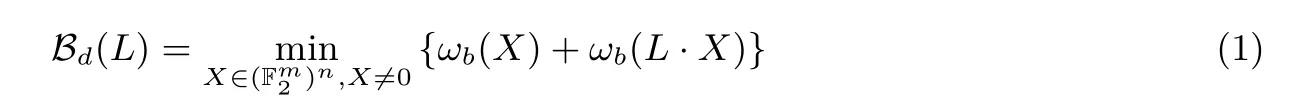
定义2 L 的线性分支数定义为:

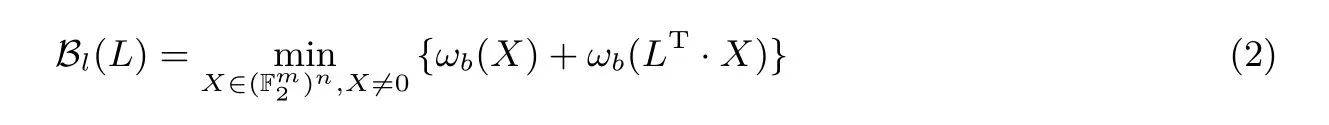
其中LT是L 的转置.

当Bd(L) = Bl(L) = n+1 时, 称分支数达到最大. 此时L 为MDS 矩阵, 其对应的线性变换L(X)称为最优线性变换或MDS 线性变换.

定义3 定义分块矩阵L=(Li,j),1 ≤i,j ≤n, 其中(Li,j) 是F2上的m 阶方阵, 则有如下形式:

其中, m ＞1 时称(L1,1,L1,2,··· ,L1,n) 为L 的首行矩阵.

定理1[11](MDS 矩阵判定定理) 假设分块矩阵L = (Li,j),1 ≤i,j ≤n, 将Li,j看作L 的1 阶子矩阵. L 为MDS 矩阵的充要条件是L 的任意t 阶子矩阵均满秩(1 ≤t ≤n).

3 基于Rotational-XOR 的线性变换

其中0 ≤li＜mn, S 是包含I 个元素的整数集合.

通过限制li的区间, 能够筛选出可能的MDS 线性变换, 因此给出依据li判断MDS 线性变换的必要条件.

引理1[23]L(X) 为MDS 线性变换的必要条件:

(1) 异或项数I 为奇数, 且I ≥n+1;

(2) 存在n 项li, 满足mi ≤li＜m(i+1).

根据引理1 可知MDS 线性变换异或项数的最小值为n+1, 因此本节研究I =n+1 时的线性变换.

其中0 ≤li＜mn, li两两互不相等.

由引理1 可知, 此时L(X) 中仅第n+1 项ln的区间不受限制, 因此约定ln为自由项. 为表述方便,将公式(5)中的li按照从小到大的顺序排列, 即令li＜li+1恒成立.

假设自由项位于区间[0,m) 内, 线性变换L(X) 可表示为:

其中0 ≤di＜m,0 ≤i ＜n+1, d1为自由项.

定义4 若矩阵的每行元素均由前一行各元素依次循环右移一个位置得到, 则称这个矩阵为循环矩阵,形式为:

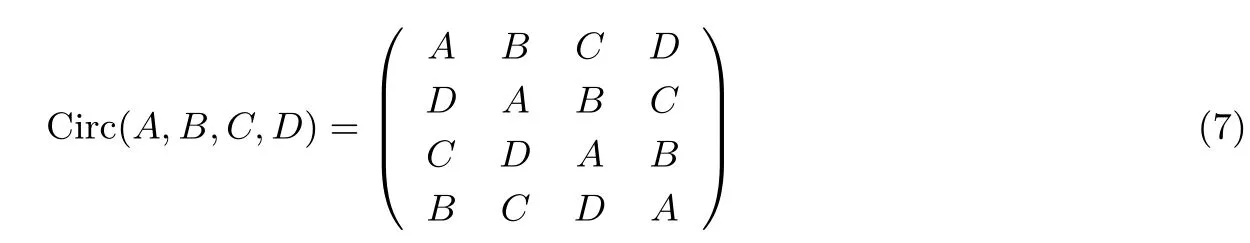
其中A,B,C,D 既可以是单个元素, 也可以是t 阶方阵(t ＞1).

线性变换L(X) 对应的矩阵L 就是一个循环矩阵, 可表示为L = Circ(L1,L2,··· ,Ln), 其中Li表示m 阶方阵(i=1,2,··· ,n). L 首行矩阵的一般形式为图1 所示.

图1 L 首行矩阵的一般形式Figure 1 General type of first row’s matrix of L

定义5 若m 阶方阵A 表示为t 个同阶对角矩阵之和的形式, 可定义为:

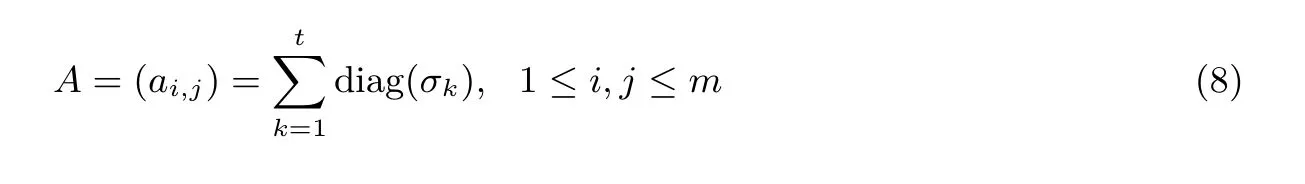
其中ai,j是F2中的一个元素, diag(σk) 表示m 阶对角矩阵. diag(σk) 在所有j-i = σk的位置上都满足ai,j=1, 其余位置上满足ai,j=0.

满足定义5 的方阵均可表示为多个同阶对角矩阵之和的形式. 例如图2 中的矩阵可表示为A=diag(5)+diag(0)+diag(-3).

图2 A 的对角矩阵表示形式: A=diag(5)+diag(0)+diag(-3)Figure 2 Representation of diagonal matrix of A: A=diag(5)+diag(0)+diag(-3)

引理2 L(X) 是MDS 线性变换的必要条件是:

(1) d0／=d1;

(2) di≥di+1, 其中i=2,3,··· ,n-1;

(3) max{d0,d1}≥d2;

(4) min{d0,d1}≤dn.

证明: 假设L 是MDS 矩阵, 根据定理1, L 的所有1 阶子矩阵均满秩.

(1) 若d0=d1, 则L1定为奇异矩阵, 因此d0／=d1;

(2) 若di＜di+1,则Li+1中元素个数小于m,即Li+1是奇异矩阵,因此di≥di+1(i=2,3,···,n-1);

(3) 假设d0＜d1, 若此时d1＜d2, 则L2中元素个数小于m, 即L2是奇异矩阵, d1＜d0时同理,因此需满足max{d0,d1}≥d2;

(4) 假设d0＜d1, 若此时d0＞dn, 则L1中元素个数小于m, 即L1是奇异矩阵, d1＜d0时同理,因此需满足min{d0,d1}≤dn;综上所述, 引理2 得证.

引理3[26]若L = Circ(L1,L2,··· ,Ln) 是MDS 矩阵, 当L 首行有两个连续相同的矩阵块时, 其它任意两个连续矩阵块之和都应是非奇异的.

推论1 若L=Circ(L1,L2,··· ,Ln) 是MDS 矩阵, 则L 中不可能有连续三个矩阵块相同.

证明: 假设L1= L2= L3, 显然L2+L3是奇异矩阵, 不满足引理3, 因此MDS 矩阵L 中不存在连续三个矩阵块相同的情况.

4 I = 9 时有限域(F82)8 上基于Rotational-XOR 的MDS 线性变换的存在性证明

基于Rotational-XOR 的线性变换可用一个循环矩阵乘以一个向量来表示, 所以通过研究循环矩阵L的性质可确定()8上MDS 线性变换的存在性. 根据引理1, 有限域()8上基于Rotational-XOR 的MDS 线性变换最小异或项数为9 项. 令I = 9 且自由项d1位于区间[0,m), L 首行矩阵的一般形式为图3 所示(假设d0＜d1).

为了简化, 可用(d0,d1,d2,d3,d4,d5,d6,d7,d8) 唯一地表示一个线性变换(例如图4 表示线性变换(0,1,1,1,1,1,1,1,1)). 显然,图3 中矩阵C 至矩阵H 均由两个对角矩阵构成,可表示为diag(α)+diag(-β).

引理4[26]m 阶方阵A=diag(α)+diag(-β)(其中α,β ＞0) 是非奇异的当且仅当(α+β)|m.

图3 I =9 时L 首行矩阵的一般形式Figure 3 Representation of diagonal matrix of L when I =9

图4 (0,4,4,4,4,4,4,4,4) 的首行矩阵Figure 4 First row’s matrix of (0,4,4,4,4,4,4,4,4)

在表1 中, 行表示diag(α), 列表示diag(-β). 令-β = di-8, α = di+1, “✓” 表示这两个对角矩阵之和满秩.

表1 ()8 上的所有满秩矩阵A, 其中A = diag(α)+diag(－β),α,β ＞0Table 1 All non-singular matrix A on ()8, where A = diag(α)+diag(－β),α,β ＞0

表1 ()8 上的所有满秩矩阵A, 其中A = diag(α)+diag(－β),α,β ＞0Table 1 All non-singular matrix A on ()8, where A = diag(α)+diag(－β),α,β ＞0

-β α 1 2 3 4 5 6 7-1✓ ✓ ✓-2 ✓ ✓-3 ✓ ✓-4 ✓-5 ✓-6 ✓-7 ✓

表2 I = 9 时集合{4} 所有可能的MDS 线性变换Table 2 All possible MDS linear transformation in {4} when I = 9

由表3 可知, 确定集合后di必须按照集合中元素的顺序依次选取. 下面对不同类型的集合分别证明.

表3 I = 9 时集合{4} 所有可能的MDS 线性变换Table 3 All possible MDS linear transformation in {4} when I = 9

(1) 集合中只有一个元素. 此时共有5 种集合可选, 分别是: {1},{2},{3},{4},{0}. 不失一般性地假设di取自集合{4}. 如图4 所示, 线性变换(0,4,4,4,4,4,4,4,4) 的首行矩阵中B =C =D =E =F =G=H, 与推论1 矛盾, 所以(0,4,4,4,4,4,4,4,4) 不是MDS 线性变换;

(2) 集合中有两个元素. 此时共有4 种集合可选, 分别是: {1,0}, {2,0},{3,0},{4,0}. 不失一般性地假设di取自集合{4,0}, 根据引理1 可知d0≤d8, 因此有d0= 0. 由表3 可知此时至少有4 个di取值相同, 与之对应, 一定有某三块连续的矩阵块相同. 如图5 所示, 线性变换(0,4,4,4,4,0,0,0,0)的首行矩阵中B = C = D 且F = G = H, 与推论推论1 矛盾, 所以(0,4,4,4,4,0,0,0,0) 不是MDS 线性变换.

图5 (0,4,4,4,4,0,0,0,0) 的首行矩阵Figure 5 First row’s matrix of (0,4,4,4,4,0,0,0,0)

由表4 可知, 确定集合后, di必须按照集合中元素的顺序依次选取. 下面对不同类型的集合分别证明.

(1) 集合中只有一个元素. 此时共有4 种集合可选, 分别是: {5},{6},{7},{0}. 不失一般性地假设di取自集合{5}. 如图6 所示, 线性变换(0,5,5,5,5,5,5,5,5) 的首行矩阵中B = C = D = E = F =G=H, 与推论推论1 矛盾, 所以(0,5,5,5,5,5,5,5,5) 不是MDS 线性变换;

(2) 集合中有两个元素. 此时共有9 种集合可选, 分别是: {5,1},{5,0},{1,0},{6,2},{6,0},{2,0},{7,1},{7,3},{7,0}. 不失一般性地假设di取自集合{5,1},此时至少有4 个di取值相同,与之对应,一定有某三块连续的矩阵块相同. 如图7 所示,线性变换(0,5,5,5,5,1,1,1,1)的首行矩阵中B =C =D且F =G=H, 与推论推论1 矛盾, 所以(0,5,5,5,5,1,1,1,1) 不是MDS 线性变换;

(3) 集合中有三个元素. 此时共有4 种集合可选, 分别是: {5,1,0},{6,2,0},{7,1,0},{7,3,0}. 不失一般性地假设di取自集合{5,1,0}, 由表4 可知此时至少有3 个di的取值相同. 如图8 所示, 线性变换(0,5,5,5,1,1,1,0,0) 的首行矩阵中B = C, 并且G 与H 之和为奇异矩阵, 与引理3 矛盾, 所以(0,5,5,5,1,1,1,0,0) 不是MDS 线性变换.

表4 d0 = 0 及I = 9 时集合{5,1,0} 所有可能的MDS 线性变换Table 4 All possible MDS linear transformation in {5,1,0} when d0 = 0 and I = 9

图6 (0,5,5,5,5,5,5,5,5) 的首行矩阵Figure 6 First row’s matrix of (0,5,5,5,5,5,5,5,5)

图7 (0,5,5,5,5,1,1,1,1) 的首行矩阵Figure 7 First row’s matrix of (0,5,5,5,5,1,1,1,1)

图8 (0,5,5,5,1,1,1,0,0) 的首行矩阵Figure 8 First row’s matrix of (0,5,5,5,1,1,1,0,0)

其余线性变换的证明过程类似于这三种形式, 且结果均与推论1 或引理3 矛盾, 此处不再赘述. 因此当d0=0 且I =9 时, 有限域()8上不存在MDS 线性变换.

引理7 当d0／=0 且I =9 时, 有限域()8上不存在MDS 线性变换.

证明: 根据引理2 可知d0≤d8, 所以当d0／= 0 时, 有d8／= 0. 已知d1＞4, 为使所有一阶子矩阵满秩, di(i=2,··· ,8) 的取值集合共有8 种, 分别是: {5,1},{6,2},{7,1},{7,3},{5},{6},{7},{0}. 确定集合后, di必须按照集合中元素的顺序依次选取. 下面对不同类型的集合分别证明.

(1) 集合中只有一个元素. 此时共有4 种集合可选, 分别是: {5},{6},{7},{0}. 不失一般性地假设di取自集合{5}. 如图9 所示, 线性变换(3,5,5,5,5,5,5,5,5) 的首行矩阵中C = D = E = F = G = H, 与推论1 矛盾, 所以(3,5,5,5,5,5,5,5,5) 不是MDS 线性变换;

图9 (3,5,5,5,5,5,5,5,5) 的首行矩阵Figure 9 First row’s matrix of (3,5,5,5,5,5,5,5,5)

(2) 集合中有两个元素. 此时共有4 种集合可选, 分别是: {5,1},{6,2},{7,1},{7,3}. 不失一般性地假设di取自集合{5,1}, 此时至少有4 个di取值相同, 与之对应, 一定有某三块连续的矩阵块相同. 如图10 所示, 线性变换(1,5,5,5,5,1,1,1,1) 的首行矩阵中C = D 且F = G = H, 与推论1 矛盾, 所以(1,5,5,5,5,1,1,1,1) 不是MDS 线性变换.

图10 (1,5,5,5,5,1,1,1,1) 的首行矩阵Figure 10 First row’s matrix of (1,5,5,5,5,1,1,1,1)

其余线性变换下的证明过程类似于这两种形式, 且结果均与推论1 矛盾, 此处不再赘述. 因此d0／= 0且I =9 时, 有限域()8上不存在MDS 线性变换.

上述证明过程中, 限定自由项d1位于区间[0,m) 内且d0＜d1. 事实上这两个限制条件对有限域()8上满足引理1 的所有9 项线性变换进行了等价划分:

(1) 根据L(X) 循环移位m 的倍数时分支数保持不变可知, 自由项d1位于区间[mt,m(t+1)),t =1,2,··· ,7, 等价于对自由项d1位于区间[0,m) 时的线性变换L(X) 循环右移mt 位, 例如线性变换(1,5,5,5,1,1,0,0,0) 和线性变换(0,1,5,5,5,1,1,0,0) 的分支数相同, 但前者的自由项位于区间[0,8), 后者的自由项位于区间[8,16), 如图11 所示线性变换(0,1,5,5,5,1,1,0,0) 等价于对线性变换(1,5,5,5,1,1,0,0,0) 循环右移8 位, 因此MDS 线性变换不存在的结论在d1位于其它区间时仍然成立;

(2) d0和d1均位于矩阵A 中, 在其余项数均不变时交换d0和d1的顺序, 线性变换不变. 例如:(1,5,5,5,5,1,1,1,1) 和(5,1,5,5,5,1,1,1,1) 是同一个线性变换. 因此令d0＜d1时证明的MDS 线性变换不存在的结论在d0＞d1时仍然成立.

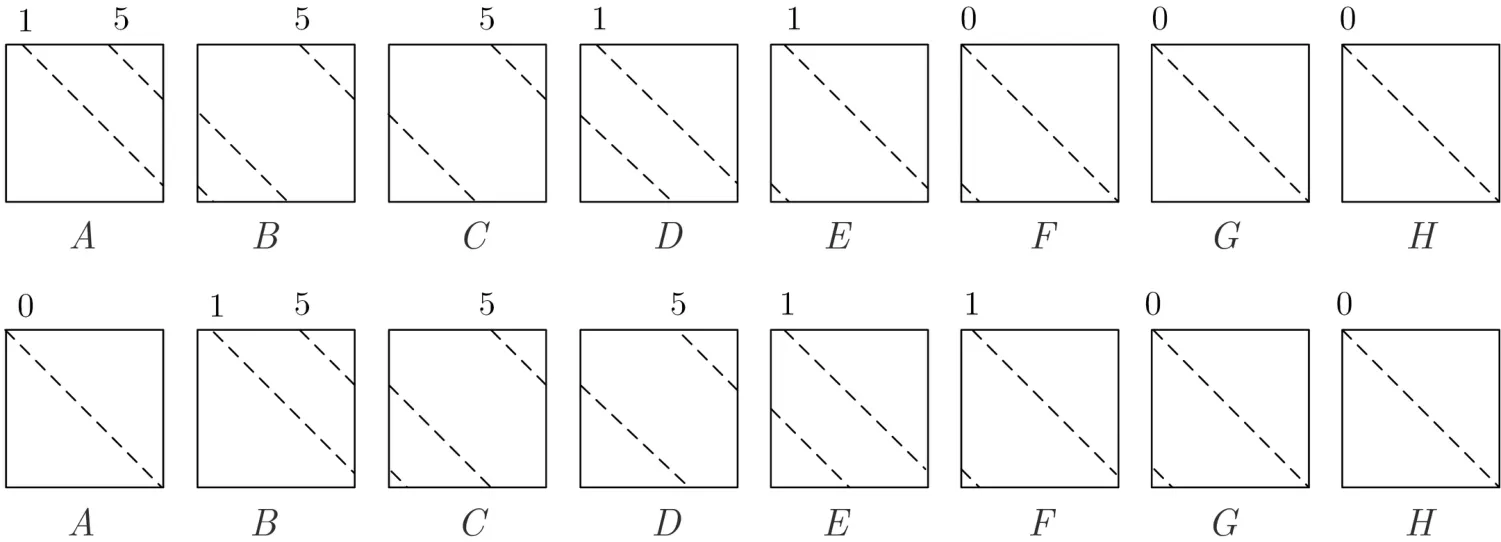
图11 (1,5,5,5,1,1,0,0,0) 和(0,1,5,5,5,1,1,0,0) 的首行矩阵Figure 11 First row’s matrix of (1,5,5,5,1,1,0,0,0) and (0,1,5,5,5,1,1,0,0)

(1) 将计数器S 的初值设置为0, S 表示I =9 时可能的MDS 线性变换个数;

(2) 共嵌套9 层循环限定di(i=0,1,··· ,8) 的范围, 其中di∈[0,8);

(3) 判断线性变换L(X) 是否满足引理2 至引理4, 若不满足任意一条引理, 将其丢弃; 否则L(X) 可能是MDS 线性变换, 令S 加1;

(4) 循环结束后返回可能的MDS 线性变换个数S.

算法1 搜索I =9 时有限域(F82)8 上可能的MDS 线性变换Input: I = 9 时有限域(F82)8 上的所有线性变换Output: MDS 线性变换的可能个数S 1 S ←0;2 for d0 ∈[0,8) do 5 if 不满足引理2 ‖ 不满足引理3 ‖ 不满足引理4 then 3 ··· //嵌套7 层循环, 限定d1 至d7 的取值区间;4 for d8 ∈[0,8) do 6 continue;7 end S++;9 end 10 ···;11 end 12 return S;8

算法1 实验环境的主要参数如表5 所示, 利用Magma 软件调用算法1, S 的返回结果为0, 进而验证了引理5 至引理7.

表5 实验环境的主要参数Table 5 Main parameters of experimental environment

综上所述, 可得到定理2.

5 I = 11 时有限域()8 上基于Rotational-XOR 的MDS 线性变换的研究

第4 节证明了异或项数取最小值9 时, 不存在基于Rotational-XOR 的MDS 线性变换. 根据引理1,有限域()8上的MDS 线性变换L(X) 异或项数至少为11 项, 因此研究I = 11 时MDS 线性变换的存在性问题. 首先将I = 11 时满足引理1 的88×56×55×54 个线性变换等价划分为15 种形式, 然后分别研究各种形式下的线性变换.

5.1 I =11 时线性变换的等价划分

根据引理1, I =11 时L(X) 中有3 个自由项, 而L(X) 对应的循环矩阵L 首行共有8 个矩阵, 因此可分为三种情况: 一个矩阵中至多有一个自由项; 存在两个自由项落在同一矩阵中; 三个自由项恰好落在同一矩阵中. 下面依次进行分析.

此处引入一种表述方法: 用三个数字表示自由项依次在L 首行矩阵块中的位置. 例如: “124” 表示自由项分别位于第一块、第二块、第四块矩阵中; “113” 表示有两个自由项位于第一块矩阵中, 第三个自由项位于第四块矩阵中; “111” 表示三个自由项均位于第一块矩阵中.

(1) 一个矩阵中至多有一个自由项第(1) 种情况共需搜索(88×7×7×7)×7×8×6 个线性变换, 如表6 所示, 共有56 种分配方式满足一个矩阵中至多有一个自由项.

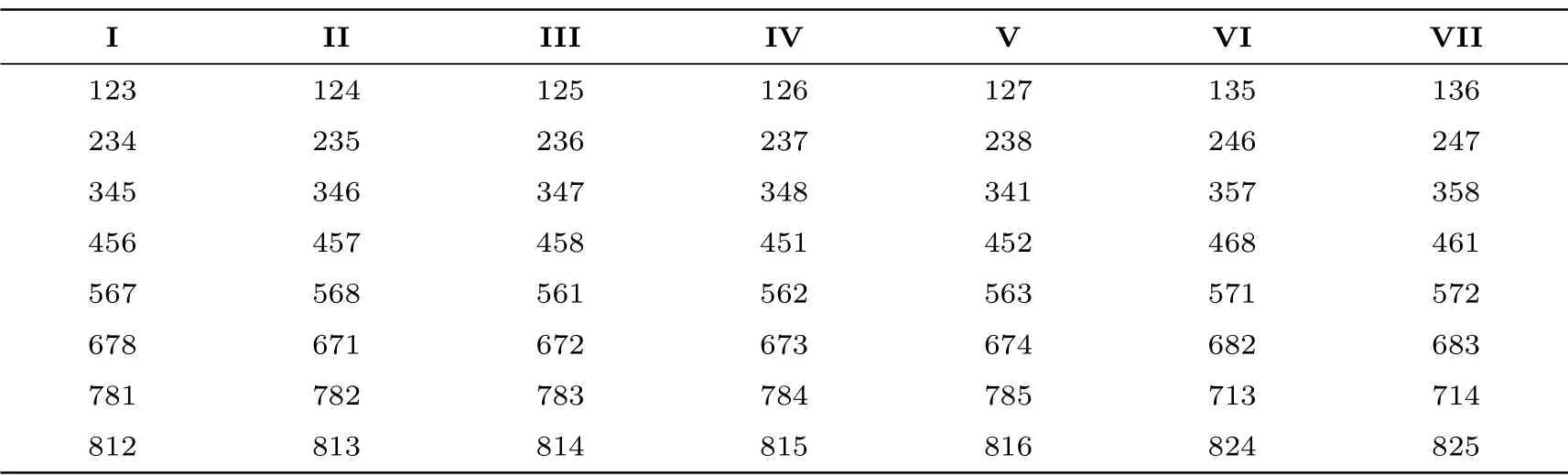
表6 一个矩阵中至多有1 个自由项的所有情况Table 6 All cases where there is at most one free term in one matrix

(a) 由于L(X) 循环移位m 的倍数时分支数保持不变, 因此表6 同列的任一行中3 个自由项位置均可由前一行循环右移一个矩阵得到, 所以同列的8 种形式等价, 首行的7 种形式涵盖了这56 种分配方式.

(b) 假设3 个自由项分别位于“123” 中, 此时自由项的全排列共有6 种方式, 它们是相等的. 例如: 3 个自由项d1,d2,d3位于“123” 中和d2,d1,d3位于“123” 中是同一个线性变换.

通过上述等价划分,同一矩阵中至多有一个自由项时共有7 种形式,分别为: “123”,“124”,“125”,“126”, “127”, “135”, “136”, 判断该情况下是否存在MDS 线性变换仅需搜索(88×7×7×7)×7个线性变换即可.

(2) 存在两个自由项落在同一个矩阵中第(2) 种情况共需搜索(88×7×6×7)×7×8×3 个线性变换, 如表7 所示, 共有56 种分配方式存在两个自由项落在同一个矩阵中.

(a) 由于L(X) 循环移位m 的倍数时分支数保持不变, 表7 同列的任一行中3 个自由项位置均可由前一行循环右移一个矩阵得到, 所以同列的8 种形式等价, 首行的7 种形式涵盖了这56种分配方式.

(b) 假设3 个自由项分别位于“113” 中, 此时自由项的全排列共有3 种方式, 它们是相等的. 例如: 3 个自由项d1,d2,d3位于“113” 中和d2,d1,d3位于“113” 中是同一个线性变换.

表7 存在2 个自由项落在同一个矩阵的所有情况Table 7 All cases where there are 2 free terms in same matrix

通过上述等价划分,存在两个自由项落在同一矩阵时共有7 种形式,分别为: “112”,“113”,“114”,“115”, “116”, “117”, “118”, 判断该情况下是否存在MDS 线性变换仅需搜索(88×7×6×7)×7个线性变换即可.

(3) 三个自由项恰好落在同一个矩阵中第(3) 种情况共需搜索(88×7×6×5)×8 个线性变换, 如表8 所示, 共有8 种分配方式三个自由项恰好落在同一个矩阵中. 由于L(X) 循环移位m 的倍数时分支数保持不变, 所以表8 中的3 个自由项位置均可由前一列循环右移一个矩阵得到, 因此这8 种形式等价. 通过上述等价划分, 三个自由项恰好落在同一矩阵块时仅有一种形式, 即“111”, 判断该情况下是否存在MDS 线性变换仅需搜索88×7×6×5 个线性变换即可.

表8 3 个自由项恰好落在同一个矩阵的所有情况Table 8 All cases where there are exactly 3 free terms in same matrix

由于(88×7×7×7)×7×8×6+(88×7×6×7)×7×8×3+(88×7×6×5)×8=88×56×55×54,因此上述等价划分方法将有限域()8上基于Rotational-XOR 的全体11 项线性变换划分为15 种不同的形式.

5.2 算法实现

对满足引理1 的线性变换进行等价划分后, 应分别搜索每种形式下MDS 线性变换的数目, 5.2 节给出通用搜索算法2. 算法步骤如下:

(1) 将计数器S 的初值设置为0, S 表示I =11 时MDS 线性变换的个数;

(2) 共嵌套11 层循环限定di(i=0,1,··· ,10) 的范围, 其中di∈[0,8);

(3) 判断线性变换L(X) 是否满足引理2 至引理4, 若不满足任意一条引理, 将其丢弃; 否则L(X) 可能是MDS 线性变换, 令S 加1;

(4) 在X ∈[0x1,0xFFFFFFFFFFFFFFFF] 上对L(X) 进行穷搜, 令count 表示某个线性变换的分支数(每次穷搜一个线性变换前置零)、x0至x7表示X 的8 个分量、y0至y7表示L(X) 的8 个分量, 若a／=0(其中a ∈[x0,··· ,x7]∪[y0,··· ,y7]), count 加1;

(5) 若X 和Y 的16 个分量中非零个数小于9, 说明L(X) 不是MDS 线性变换, 令S 减1 并退出本层循环;

(6) 循环结束后返回MDS 线性变换的个数S.

算法2 实验环境的主要参数如表5 所示. 使用Magma 软件调用算法2 对表6-表8 中15 种形式的线性变换进行等价意义下的穷搜, S 的返回值均为0. 由此给出定理3.

算法2 搜索I =11 时有限域(F82)8 上的MDS 线性变换Input: I = 11 时有限域(F82)8 上的所有线性变换Output: I = 11 时MDS 线性变换的个数S 1 S ←0;2 for d0 ∈[0,8) do 3 ··· //嵌套9 层循环, 限定d1 至d9 的取值区间;4 for d10 ∈[0,8) do 5 if 不满足引理2 ‖ 不满足引理3 ‖ 不满足引理4 then 6 continue;7 end 8 S++;9 for X ∈[0x1,0xFFFFFFFFFFFFFFFF] do 10 Y = L(X),count ←0;11 x0 = X&0x00000000000000FF;12 x1 = X&0x000000000000FF00;13 ···;14 x7 = X&0xFF00000000000000;15 y0 = Y&0x00000000000000FF;16 y1 = Y&0x000000000000FF00;17 ···;18 y7 = Y&0xFF00000000000000;19 for a ∈[x0,··· ,x7]∪[y0,··· ,y7] do 20 if a /= 0 then 21 count++;22 end 23 end 24 if count ＜9 then 25 S--;26 break;27 end 28 end 29 end 30 ···;31 end 32 return S

6 结论

本文研究并给出分组规模为64、分块规模为8 的MDS 线性变换的必要条件, 探寻该规模下的MDS线性变换. 通过分析首行矩阵的性质, 证明此规模下异或项数取最小值9 项时不存在MDS 线性变换, 并利用Magma 软件验证该结论. 进而研究异或项数为11 项时的MDS 线性变换, 得出此规模下异或项数取11 项时也不存在MDS 线性变换. 这两个结论为之后设计有限域()8上基于Rotational-XOR 的MDS 扩散层提供了理论参考.

在未来工作中, 一方面, 我们会继续研究异或项数为13 项时有限域(F82)8上的MDS 线性变换的存在性问题; 另一方面, 若降低一部分对安全性的需求, 也可研究有限域()8上的类MDS 线性变换.