关于半对偶模的弱Ding-投射模

何东林， 樊 亮

(陇南师范高等专科学校数信学院， 甘肃 陇南 742500)

引 言

Gorenstein同调理论是相对同调代数的研究热点之一，许多学者先后对其进行了研究和推广。特别地，Holm和Jørgensen[1]在交换Noether环上引入了C-Gorenstein投射模和C-Gorenstein内射模的概念，并研究了与其相关的投射模类。White[2]进一步讨论了一般交换环上的C-Gorenstein投射模和C-Gorenstein内射模，并称之为GC-Gorenstein投射模和GC-Gorenstein内射模。Gillespie[3]介绍了Ding-投射模和Ding-内射模。Ding-投射模与强Gorenstein平坦模[4]是一致的，而Ding-内射模与Gorenstein FP-内射模是一致的。为了研究Ding-投射模和Ding-内射模的可数部分及相关的投射和内射模类，Zhang等[5]引入了DC-投射模和DC-内射模。f-投射模[7]是投射模的一个重要推广，每个投射模都是f-投射模，每个f-投射模都是平坦模，但反之不真。C-Gorenstein投射模与C-投射模[8]密切相关，DC-投射模与C-平坦模[8]密切相关。Mao[9]引入的关于半对偶模C的C-f-投射模是介于C-投射模与C-平坦模之间的一类模。因而，可考虑与C-f-投射模密切相关的模类。本文主要研究关于半对偶模C的弱Ding-投射模(即弱DC-投射模)，并讨论弱DC-投射模与DC-投射模及C-Gorenstein投射模之间的关系，以及弱DC-投射模的若干性质和等价刻画。

1 定义和引理

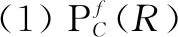
引理2[9]设M是R-模，则

(2)M是C-f-投射模当且仅当HomR(C,M)是f-投射模。

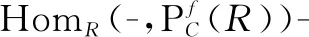
其中Pi(i∈Ζ)是投射R-模，使得M≅Coker(P1→P0)。用wDPC(R)表示所有弱DC-投射模组成的类。

引理3以下说法成立：

(1)DPC(R)⊆wDPC(R)⊆GPC(R)。

(2)当R是Noether环时，弱DC-投射模与DC-投射模一致，从而DPC(R)=wDPC(R)。

引理4[8]设0→X′→X→X″→0是R-模正合列。若X′和X″是C-投射模，则该正合列可裂且X也是C-投射模。

2 主要结果

定理1设M是R-模，则以下条件等价：

(1)M是弱DC-投射模。

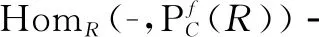
(1)

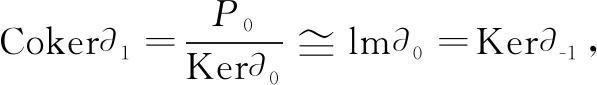
…→P1→P0→M→0，

(2)

(3)

0→HomR(M,Q)→HomR(P0,Q)→HomR(P1,Q)→…

(4)

其中Pi(i<0)是投射R-模。不妨取M的投射分解

…→P1→P0→M→0，

(5)

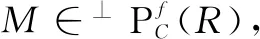
其中Pi(i∈Ζ)是投射R-模，使得M≅Coker(P1→P0)。因此M是弱DC-投射模。

定理2设M是弱DC-投射模，如果存在正合列

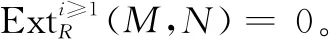
定理3设P是有限生成投射模且M是弱DC-投射模，则HomR(P,M)是弱DC-投射模。

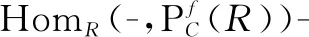
(6)

其中Pi(i∈Ζ)是投射R-模，使得M≅Coker∂1。因为P是有限生成投射模，所以用函子HomR(P,-)作用于序列(6)后仍正合，即序列

正合，且HomR(P,M)≅Coker(HomR(P,∂1))。因为P是有限生成投射模且R为交换环，根据文献[14]中命题20.10可得，对任意整数i<0，有同构

由文献[15]中P14stability中第6条可得，HomR(P,Pi)(i∈Ζ)是投射模。从而有正合列

(7)

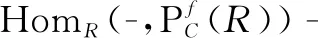
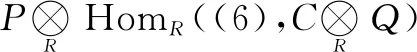
综上所述，HomR(P,M)是弱DC-投射模。

证明证明过程与定理3对偶。

定理5设M是任意R-模，则存在正合列…→W1→W0→M→0，其中Wi(i≥0)是弱DC-投射模。

证明设M是任意R-模，由文献[6]中命题1.8可得，M具有DC-投射分解，即存在正合列

…→W1→W0→M→0

其中Wi(i≥0)是DC-投射模。又由引理3知，DPC(R)⊆wDPC(R)，所以Wi(i≥0)是弱DC-投射模。

定理6弱DC-投射模类wDPC(R)关于任意扩张封闭。

图1 正合交换图

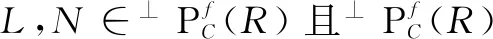
定理7弱DC-投射模类wDPC(R)关于任意满同态的核封闭。

证明由定理1和Ext函子的性质可证。

定理8弱DC-投射模类wDPC(R)关于任意满同态的核封闭。

定理9弱DC-投射模类wDPC(R)是投射可解的且关于任意直和因子封闭。

证明由引理3及文献[6]中命题1.8知，wDPC(R)包含所有投射模。根据定理6和定理8可得，wDPC(R)关于任意扩张和满同态的核封闭。从而弱DC-投射模类wDPC(R)是投射可解的。又因为wDPC(R)关于任意直和封闭，由文献[16]中命题1.4可得，wDPC(R)关于任意直和因子封闭。

3 结束语

利用环模理论和同调代数的方法，讨论了弱DC-投射模与DC-投射模及C-Gorenstein投射模之间的关系。研究了弱DC-投射模的若干性质和等价刻画。结果表明：所有弱DC-投射R-模组成的类是投射可解的且关于任意直和因子封闭。从而补充了Gorenstein同调代数中的相关理论，并进一步完善了对Gorenstein模类及其维数后续问题的研究，具有一定的理论价值。