基于扩展有限元法的表面裂纹平板拉伸极限载荷研究

孙国栋， 刘宇杰， 康国政

(西南交通大学力学与工程学院， 成都 610031)

引 言

裂纹导致的工程构件失效，在现代工业结构和机械中屡屡发生。对于含裂纹的工程构件进行断裂力学评定对于结构的设计和安全评估是非常重要的。自20世纪50年代以来，以线弹性断裂力学和弹塑性断裂力学为代表的断裂力学理论和方法得到了迅速发展和应用。然而，大多数的经典断裂力学理论和成熟的设计规范都是基于二维断裂理论的。对于断裂韧性、裂纹扩展速率等材料断裂特性的标准测试也多基于二维穿透型裂纹来开展试验的。通常在裂纹扩展问题的断裂分析中，判断裂纹进入临界失稳断裂状态的方法是当裂纹尖端附近的应力强度因子值K等于材料试验测得的断裂韧性KIC时，认为裂纹将要失稳扩展。Coppe等[1]在计算裂纹体的剩余寿命时，判断停止计算的临界裂纹尺寸是工程上给定的一个希望修复的裂纹尺寸，同时也指出了一般使用材料的断裂韧性来计算临界裂纹尺寸。杨海宾等[2]在计算车体的剩余寿命时，判断计算停止的条件是应力强度因子值等于材料的断裂韧性值，即根据施加载荷的大小和裂纹扩展到某一长度时计算出的应力强度因子值等于临界应力强度因子值时停止计算剩余寿命。高云等[3]在计算裂纹体的剩余寿命时，停止计算裂纹扩展的条件也是某一裂纹长度计算出的应力强度因子值达到材料断裂韧性时，裂纹停止扩展。由于几何和受力的复杂性，大部分实际裂纹问题的裂纹尖端附近的应力场是三维应力场。Yuan和Brocks[4]的研究表明，三维应力下的约束情况对材料的断裂行为有显著的影响。在国内，郭万林院士课题组[5-7]开展了大量的应力约束条件下的三维裂纹断裂研究，建立了双参数K-Tz或J-Tz模型，取得了良好的效果。由于断裂问题的复杂性，大量的断裂问题研究还是必须借助有限元分析来开展。最早由美国西北大学的Belytschko和Black[8-9]提出的扩展有限元方法(Extended Finite Element Method, XFEM)是在标准有限元框架下，在不连续的间断区域引入新的能够反映间断特性的的位移函数。扩展有限元方法在处理裂纹问题时，能够避免繁琐的裂纹网格重划分，在相对较为粗糙的裂尖网格下获得比较精确的数值解。因此扩展有限元方法在裂纹扩展、动态断裂等方面得到越来越多的应用。大量学者[10-12]基于扩展有限元方法开展了大量的断裂问题研究，取得了良好的效果。

目前利用XFEM开展的断裂问题模拟，多集中于裂纹扩展分析[13-15]，应力强度因子计算[16-17]等方面，对于结构失稳断裂时极限载荷方面的研究还较少。本文首先对车钩铸造E级钢CT试样开展了断裂韧性试验，获得了材料的断裂韧性。然后基于扩展有限元方法，建立三维模型对CT试样在试验中的裂纹扩展过程进行了模拟，通过与试验获得的载荷-裂纹张开位移曲线的对比，验证数值模拟的合理性。进而对带有椭圆形表面裂纹的不同厚度的平板的断裂行为进行了模拟，获得了不同情况下带表面裂纹平板的拉伸极限载荷，并与通常利用材料断裂韧性来确定的拉伸极限载荷进行了对比研究。

1 扩展有限元法

扩展有限元法是在传统有限元方法的基础上进行重要改进而提出的方法，核心思想是在常规有限元位移函数的基础上，引入一些加强函数以反映间断问题的不连续性。间断问题分为强间断(位移不连续)和弱间断(位移导数不连续)两种，在扩展有限元中要采用不同形式的加强函数。

在使用扩展有限元法分析裂纹问题时，由于裂纹两侧位移被间断，所以要选用处理强间断问题的加强函数，在扩展有限元中经过加强的位移模式表示为[8]：

(1)

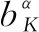
图1所示为对裂纹尖端附近的一层节点进行加强时的节点分布，其中“○”表示裂纹尖端所处单元的节点，“□”表示裂纹贯穿单元的节点，其余均为常规节点(图中没有标出)。

图1 XFEM中节点分布

式(1)中等号右边：第一项代表没有被裂纹影响到的单元区域，和传统有限元方法的形函数完全一致；第二项代表被裂纹贯穿的单元区域；第三项代表裂纹尖端所处的单元区域，其中，α=1,2,3,4，裂纹尖端渐进位移场的附加函数φα(x)的具体表达形式为[9]：

(2)

式(2)中：(r,θ)表示裂尖的极坐标系，r为节点到裂尖的距离，θ表示节点和裂尖之间连线的角度，裂尖切线方向θ为0°。

2 车钩铸造E级钢断裂韧性试验及模拟

2.1断裂韧性试验

根据GB/T 21143-2014《金属材料准静态断裂韧度的统一试验方法》，采用如图2所示的带有侧槽的CT试样进行断裂韧性试验。在进行断裂韧性试验前，在低载荷下进行了疲劳预制裂纹，保证裂纹前缘的尖锐，疲劳预制裂纹时的裂纹扩展量约为2 mm。在疲劳预制裂纹完成后以0.01 mm/s的位移速率控制加载直至断裂，得到如图3所示的载荷-裂纹张开位移曲线。对试验数据进行处理，若用K因子来表征该材料的断裂韧性值，其大小为5045 MPa*mm1/2。

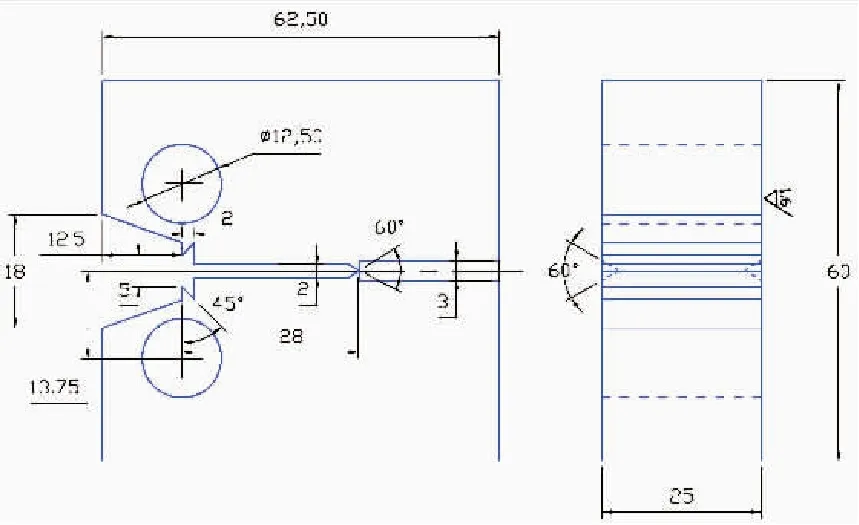
图2 带有侧槽的CT试样几何尺寸

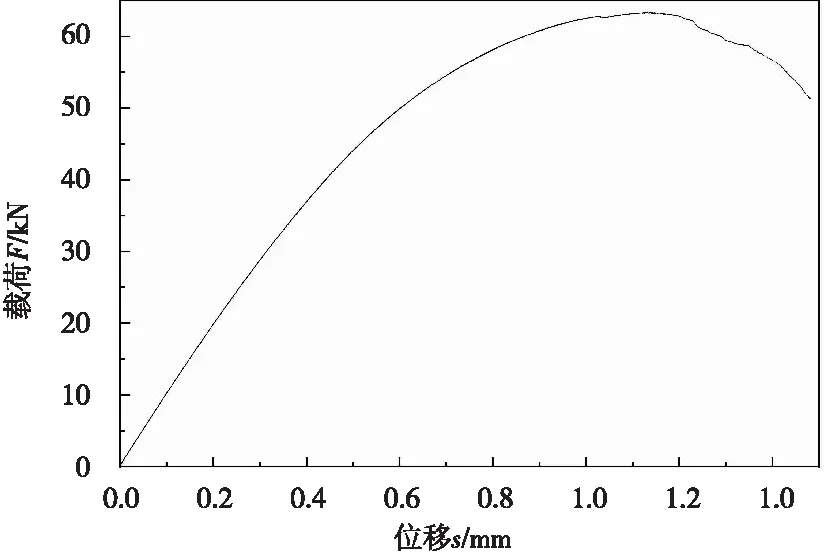
图3 断裂韧性试验中的载荷-裂纹张开位移曲线寸

2.2扩展有限元模拟

在ABAQUS软件中根据图2所示的CT试样尺寸建立如图4所示的有限元模型。试验中通过穿过上下两个孔的销钉施加位移载荷，建立了两个设置为刚体的圆棒状的销钉，建立两个参考点分别和两个销钉耦合，以便施加位移载荷和获取载荷数据，销钉表面和CT试件圆孔之间设置面面接触，使其接触时可以滑动，使有限元模拟更加接近试验时的真实情况。

图4 CT试样的有限元模型

在材料属性中设置弹性模量为206915 MPa，泊松比为0.3，屈服强度值为640 MPa，抗拉强度值为805 MPa，这些材料参数均通过对圆棒试样的拉伸试验获得。裂纹设置为XFEM裂纹类型，裂纹的长度设置为疲劳预制裂纹后的长度30 mm，裂纹面和CT试件之间设置为切向无接触，法向硬接触的接触属性。损伤演化采取最大主应力准则，最大主应力设置为805 MPa，即为材料的抗拉强度值，裂纹扩展所需能量设置为1220 N/m。网格划分采用C3D8H单元，在裂纹附近采用结构化网格，在孔周围采用自由网格，并在裂纹附近进行网格加密。加载边界条件设置为在上端参考点RP-3上施加位移载荷，下参考点RP-1固定。待计算完毕后提取加载点的载荷和缺口处的位移，形成载荷-裂纹张开位移曲线和试验数据进行对比。扩展有限元模拟得到的载荷-裂纹张开位移曲线和试验结果对比如图5所示。

图5 CT试样有限元模拟结果

从图5可以看出，有限元模拟得到的轴向载荷-裂纹张开位移曲线和试验曲线的趋势一致，有限元模拟曲线略高于试验曲线。原因可能在于，在有限元模拟中下参考点RP-1采用了固定约束，而在实际中，由于试验机夹具不可能是无限大，与加载销钉关联的下参考点并不能保持完全固定。因此模拟曲线的刚度比试验曲线略高。从最大载荷的数值上看，有限元模拟的最大载荷为65.154 kN，试验中最大载荷为63.112 kN，两者仅相差3.1%，由此验证了本文有限元模拟的准确性。

3 受拉伸的带表面裂纹平板的扩展有限元模拟

3.1有限元模型与计算流程

在ABAQUS中建立如图6所示的平板有限元模型，初始裂纹形状设置为半椭圆表面裂纹，位于平板侧边中部。平板的厚度(B)分别为：2 mm，4 mm，8 mm，16 mm，32 mm，64 mm，宽度62.5 mm,高60 mm。裂纹尺寸为2a/B=0.5,c/a=0.6，其中2a代表裂纹长度，c代表裂纹深度。在平板的上下顶面施加位移，对带表面裂纹的平板受到拉伸载荷作用时的断裂行为进行模拟。在裂纹扩展区域对网格进行加密，单元类型设置为C3D8H。在平板上下表面外，分别设置两个参考点和上下表面的全部节点进行耦合，在两个参考点上施加与裂纹面垂直方向的位移载荷，在后处理结果中提取参考点的载荷-位移曲线。材料参数与裂纹属性设置与2.2节中设置一致。

图6 带表面裂纹的平板的有限元模型

在ABAQUS软件的后处理模块中，可以输出每一分析步对应的裂纹尺寸和拉伸载荷值，直接得到裂纹扩展过程中的载荷-位移曲线，并得到最大极限载荷。但是并不能动态输出应力强度因子K的数值。为获得应力强度因子K达到材料断裂韧性时对应的极限载荷，还需要进行静态应力强度因子的计算。在进行静态应力强度因子计算时，将裂纹设置为不能扩展，并在结果文件中输出对应裂纹的K因子值，每一次计算只能得到固定裂纹尺寸的应力强度因子的值。为得到应力强度因子随裂纹尺寸的变化，就需建立不同裂纹尺寸的几何模型来得到相应的应力强度因子。当计算出的K因子达到试验获得的材料断裂韧性时，输出此时的载荷，并与按照扩展有限元能量准则计算出的扩展过程中的最大载荷进行对比。

3.2模拟结果与讨论

图7给出了扩展有限元模拟得到的厚度为16 mm的带表面裂纹平板的载荷-位移曲线，这里的位移选取为上下表面参考点的相对位移。整个曲线大致可分为三个阶段：第一阶段，当位移较小时，载荷和位移之间几乎呈线性关系，载荷和位移成比例增大；第二阶段，载荷随位移缓慢增加，裂纹稳定扩展；第三阶段，载荷随位移的增大而下降，进入裂纹失稳扩展阶段，直至完全断裂。 在图7给出的16 mm厚平板的扩展有限元模拟载荷-位移曲线中，最大载荷为779.96 kN。在常规有限元计算中，带裂纹结构能承受的最大载荷使用强度因子准则来确定, 即将裂纹尖端最大应力强度因子K达到断裂韧性KIC时对应的载荷作为结构能承受的最大载荷值。若采用强度因子准则，对于本节计算的16 mm厚带表面裂纹平板能承受的最大载荷为599.21 kN，这比用扩展有限元法的能量准则计算出的最大载荷要低23.2%。这说明按照传统的平面断裂准则得到的极限载荷比按照三维裂纹准则得到的极限载荷要低，采用传统的平面断裂准则在三维裂纹情况下偏保守。

图7 16 mm带裂纹平板载荷-位移曲线计算结果

在ABAQUS扩展有限元模块中可以输出场变量PHILSM(Signed distance function to describe the crack surface)来描述裂纹面。图8给出了裂纹扩展过程中的PHILSM的变化，图中蓝色部分表示裂纹面。图8(a)为初始裂纹形状，图8(b)为裂纹沿深度扩展1 mm之后的裂纹形状，裂纹沿宽度也同样扩展了1 mm，图8(c)为裂纹沿深度扩展2 mm之后的裂纹形状，此时裂纹沿宽度方向扩展不足2 mm，图8(d)为裂纹沿深度扩展3 mm之后的裂纹形状，也是计算KIC时的裂纹尺寸，因为裂纹形状不是十分规则，计算KIC时将其近似为一个规则圆弧进行计算。图8(e)～图8(j)分别为裂纹沿深度扩展4 mm，6 mm，8 mm，10 mm，12 mm，14 mm时的裂纹形状。这些图中可见，裂纹在深度方向上的扩展量是大大高于宽度方向上的扩展量。随着裂纹的扩展，表面裂纹逐步加深加宽，最终穿透厚度方向成为穿透型裂纹。

图8 裂纹形状变化

为了讨论厚度对包含表面裂纹平板极限载荷的影响，本文计算了平板的厚度(B)分别为：2 mm，4 mm，8 mm，16 mm，32 mm，64 mm，宽度为62.5 mm，高为60 mm，裂纹尺寸为2a/B=0.5,c/a=0.6，共6种厚度情况下含表面裂纹平板的拉伸裂纹扩展情况。图9给出了6种厚度下带表面裂纹平板在拉伸情况下的载荷-位移曲线。

图9 不同厚度平板的载荷-位移曲线

从载荷-位移曲线的变化趋势上看，厚度影响不大，不同厚度带表面裂纹平板的载荷-位移曲线的趋势基本一致，呈现前述的三阶段的特点。随着厚度的增加，带表面裂纹平板的极限载荷在增加，同时达到极限载荷时对应的临界位移在降低。这表明随着平板厚度的增加，断裂模式从韧性断裂向脆性断裂转变。

表1给出了不同平板厚度的情况下，分别用扩展有限元能量准则得到的极限载荷和用常规应力强度因子准则得到的极限载荷。

表1XFEM求得极限载荷值和KIC对应极限载荷值对比

由表1可见，按照传统的KIC平面断裂准则计算得到的极限载荷在三维裂纹情况下偏保守。两种方法计算得到的极限载荷之间的差异随着板厚度的增加而增大。

为了进一步揭示平板厚度对极限载荷的影响，对当裂纹前缘应力强度因子达到KIC时裂纹前缘的塑性区情况进行了分析。图10给出了在计算KIC的有限元模型中提取裂纹前缘等效塑性应变(PEEQ)云图。

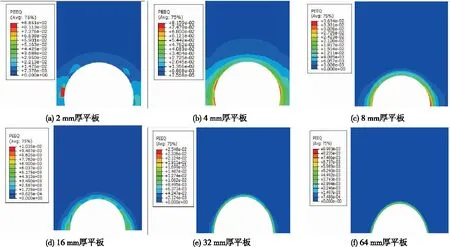
图10 应力强度因子达到KIC时的塑性区

从图10可以看出，在平板厚度较小时，塑性区的面积比较大，随着平板厚度的增加，裂纹前缘的塑性区逐步减小。在平板厚度较小时(如2 mm厚，4 mm厚)，裂纹前缘附近均发生塑性变形，这与穿透型裂纹达到临界扩展时塑性区的分布相似，故两种方法计算出的极限载荷更加接近。而在厚板的情况下，由于有较强的约束，导致应力强度因子达到KIC时，裂纹尖端塑性区很小，这与达到临界扩展时裂尖塑性区比较大的状态有较大区别，故按照KIC计算出的极限载荷比扩展有限元计算的结果要低很多。

4 结 论

(1)利用ABAQUS的扩展有限元模块，设置合理参数对车钩E级铸钢CT试样的断裂行为进行较为准确的模拟，得出载荷-裂纹张开位移曲线和试验结果吻合得很好。

(2)对不同厚度的带表面裂纹平板拉伸情况下的断裂行为模拟发现，按照材料断裂韧性KIC计算出的极限载荷在三维裂纹情况下偏保守。材料断裂韧性对应的最大载荷和扩展有限元方法计算得出的最大载荷值之间的差异随着板厚度的增加而增大。在计算表面裂纹厚板的断裂极限载荷时必须考虑裂纹的三维约束效应。