异常涡旋光束的拓扑荷的测量

余丽芳,黎 芳

(北京建筑大学理学院,北京 102616)

1 引 言

涡旋光束是近年来国际上研究的热点领域之一,已经在量子信息编码、空间信息传输与通信、遥感成像、光学微操纵、生物医学等领域得到了广泛且重要的应用[1-8]。近年来受关注较多的涡旋光束有拉盖尔-高斯(Laguerre-Gaussian,LG)光束[9-11]和复宗量拉盖尔-高斯(elegant Laguerre-Gaussian,ELG)光束[12-13]。其中ELG光束虽比普通LG光束具有更好的对称性,却一直没有得到更大的应用,限制其发展的一个主要原因是其不容易实现。2013年,异常涡旋光束(anomalous vortex beam,AVB)[14]是被提出且实验产生的一种新的涡旋光束,这种光束在远场传输后可以变成ELG光束,即它可以作为产生ELG光束,甚至更进一步产生贝塞尔-高斯光束、贝塞尔涡旋光束的光源。

涡旋光束之所以受到广泛关注主要是其每个光子具有确定的轨道角动量,其轨道角动量值仅由涡旋光束的拓扑荷决定。因此测量涡旋光束的拓扑荷对于其在各领域中的应用具有重要的意义。然而,目前针对拓扑荷的测量主要针对于LG光束[15-17],对于异常涡旋光束的拓扑荷的测量尚未见相关报道。本文提出用一种掩模板来对异常涡旋光束的拓扑荷进行测量。该方法能简单方便测量出拓扑荷,其对于促进异常涡旋旋光束在光束传输、通信遥感等领域的应用具有显著的价值。

2 理论推导

AVB在源平面z=0处的光场表达式为：

(1)

其中,C0为常数;n为AVB的阶数;m为拓扑荷;w0为束腰半径。

根据惠更斯-菲涅尔积分可以推出AVB在接收平面z处的光场表达式为:

(2)

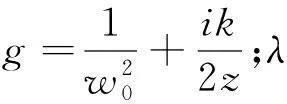
把AVB光束通过图1所示的掩模板,根据接收面上的光强图来判别AVB的拓扑荷值。该掩模板具有Q个等间距环,每个环有L个孔径。由图可知掩模板的透过率函数为:

(3)

图1 掩模板图样

当异常涡旋光束u0照射这个掩模板时,根据夫琅各费衍射公式可知,观察面上强度分布为:

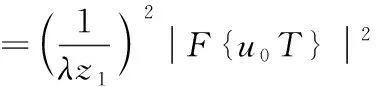
(4)

其中,z1为掩膜板到接收面的距离;F表示傅里叶变换;⊗表示卷积。

由δ函数的傅里叶变换性质可得:

(5)

对式(2)进行傅里叶变换,并利用式(6)和式(7)可得式(8):

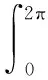
2π(-i)mJm(kρr0)exp(-imφ)

(6)

(7)

(8)

将式(5)和式(8)代入式(3)且把直角坐标系中的变量变换为极坐标系中的变量,可以得到:

(9)

再利用式(6)和式(7)解得:

(10)

3 数值仿真

为了得到光强分布图,可以对强度解析表达式(10)进行数值仿真。在仿真中,选用的AVB的波长为λ=1550 nm,光斑半径w0=1 mm。掩模板有4个环,外环半径a=1 μm,且每个环上均匀分布15个点,即Q=4,L=15。根据解析式(10)可以得到光束传输任何距离后,经掩模板作用后接收平面上的强度图。仿真发现光强图与光束的阶数无关,与拓扑荷值有关。

图2是不同拓扑荷值的异常涡旋光束在自由空间中传输了z0距离后再穿过掩模板后的强度图。由仿真结果可以得出,光强图为环状结构,而且拓扑荷值不同,对应的光强图的环数不同。如本图中光环数为4时,对应于拓扑荷为1,光环数为2时,对应拓扑荷为2,依次递减。因此,只要根据接收面上的光强图的环数就可以测量发射异常涡旋光束的拓扑荷。环数对应的拓扑荷值与每个环上的孔径数L值成正相关,即L越大,可测得的拓扑荷值越多,但是分辨率会有所下降。因此若需测量的异常涡旋光束的拓扑荷较多,可适当增加掩膜板上的孔径数。

图2 接收平面的光强图

若异常涡旋光束的拓扑荷值为零时,所得光强图(图3所示)中心不是暗芯,而为一个亮斑。因此此时无需通过环数来判断拓扑荷,由亮斑便可知拓扑荷为零。

图3 m=0时接收平面的光强图

4 结 论

本文提出用一种掩模板的方法来测量异常涡旋光束的拓扑荷值。在接收孔径之前放置一个特殊样式的掩膜板,通过接收平面的光强图来分辨异常涡旋光束的拓扑荷值。研究表明,接收平面上的强度分布图为多环结构,环数与异常涡旋光束的拓扑荷值一一对应,由光环数便可知拓扑荷值。研究成果对于促进异常涡旋光束的应用具有重要作用。