依托图式迁移促进自主建模——《笔算小数加法和减法》教学实录与评析

执教/陈静 评析/韩梅

【教学内容】

苏教版五年级上册第48~50页。

【教学过程】

一、激发兴趣，唤醒图式

师：之前的学习中，我们与小数已有了亲密的接触。今天，老师想和你们做个和小数有关的游戏。（板书：0.8）

师：用你的语言描述一下0.8，把它介绍给同伴。

生：8个0.1；十分之八；比1小0.2；80个0.01；0.7和0.9之间的一位小数……

【评析：小数的意义、计数单位、和差关系……都是本节小数加减法的学习基础和知识支撑。游戏化教学激发了学生从“数量、运算、关系”等角度描述小数的兴趣，唤醒了他们对已有知识的回忆，并激活已有的学习经验。在生生互动、师生互动中，达成对已习得小数图式的反刍与交流。】

二、丰盈图式，探究建模

1.提出问题，探究联结。

师：老师打算采购这些文具中的一样或几样：钢笔8元/支、笔记本3.4元/本、讲义夹4.75元/个、水彩笔2.65元/支。

师：根据这些信息，你能提一个用加法或者减法计算的问题吗？

生：一个讲义夹比一本笔记本多多少元？

生：买一支钢笔和一个讲义夹，一共多少元？

生：一支钢笔比一本笔记本多多少元？

生：这几类文具分别买一个需要多少元？

生：买一本笔记本和一个讲义夹，一共多少元？

师：咱们先来解决“买一本笔记本和一个讲义夹，一共多少元？”这个问题。怎么列式？

生：3.4+4.75。

师：观察这两个加数，你有什么想说的？

生：这两个加数都是小数，一个是一位小数，一个是两位小数。

生：他们可以分别转化成整数340分和475分。

生：也可以转化成3元4角和4元7角5分。

生：老师，我估算了一下，它们的得数约等于5+3=8。

师：那你估一估，这道算式的结果，到底在哪两个整数之间？

生：先把它们当成比它们小的整数、再当成比它们大的整数，结果在4+3=7和5+4=9之间。

师：结果是不是在这两个数之间呢？自己列竖式，尝试一下。

反馈：出示四位学生写的竖式。你看明白了哪道？

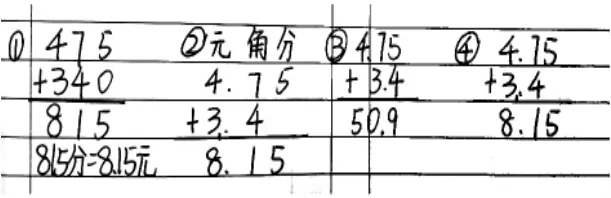
生：我看明白了第一道竖式，因为它就是我们之前研究过的整数加法。

师：笔算整数加法，有哪些算法要求？

（板书：相同数位对齐，从低位算起，满十进一）

生：我看明白了第二道竖式，它是相同数位相加，满十进一。

师：谁有疑问？

质疑1：从低位算起，这个3.4的最低位4为什么不和4.75最低位的5相加？就像第三种方法那样。

生：4代表的是四角，而5代表的是五分。

质疑2：那3元4角后面是几分呢？

生：它的后面有一个隐藏的零，代表0分。

师：小数的末尾添上0，小数的——（学生回忆小数的性质）

师：第三种方法是“从低位算起”吗？

生：不是，这里的“低位”指的是两个加数相同的最低数位。

小结：同学们真是善于用联系的眼光看问题，用源于生活的思考，发现了小数加法与整数加法“相同数位”之间的联系；用源于小数意义的思考，发现了“从低位算起”的实质。

师：谁来评价第四种方法？

生：第四种方法是正确的，它关注到了相同数位对齐，从低位算起，满十进一。

师：在小数中，“相同数位对齐”其实也就是关注到了什么？

生：小数点对齐。

师：“小数点对齐”指的是哪几个数中的小数点对齐？

生：加数、和。

师：看一下计算的结果，与估算的结果差不多吗？在估算的范围内吗？

【评析：本环节通过学生熟悉的文具采购问题切入，将数学知识自然融入到现实生活中，学生源于生活经验提出多个问题。解决问题时，教师通过引导学生观察算式，实现小数到整数的转化、数到量的转化，并适时渗透了估算意识。笔算方法的形成过程是先由学生尝试解决，再交流总结得出的。抓住学生在探究算法的过程中生发出的“整数竖式”“量的竖式”突破本节课教学难点，让学生深入思考、群体分享、互动质疑，加深了对小数加法的算理、算法的理解。】

2.算法迁移，助力建模。

师：接下来研究一个类别不一样的问题——

生：一个讲义夹比一本笔记本多多少元？

师：类别不一样在哪儿？

生：这是用小数减法计算的问题，算式是：4.75-3.4。

师：你能利用刚刚学习小数加法的经验，试着解决这道小数减法吗？

师：说说小数减法列竖式计算时要注意些什么，为什么？

强调：相同数位对齐，从低位算起。

师：如果某一位不够减，要怎么办？

生：退一当十。（板书）

【评析：学生在经历过探究小数加法的计算方法后，已经对“相同数位对齐”“小数点对齐”“从低位算起”有了较好的理解，此时引导他们将小数加法的算理、算法迁移至小数减法的笔算中，运用探索小数加法时积累的学习经验，通过观察、思考、操作、归纳等活动，充分经历小数减法运算方法自我建构过程，体会小数计算的价值，助力加、减法图式建模的达成。】

3.引导检验，沟通联结。

师：这两道算式的运算过程可以互用作彼此的检验方法吗？

师：还有没有其他的检验方法呢？

生：加法还可以使用交换律进行检验。

生：减法也可以用“被减数-差=减数”进行检验。

师：选择一种方法检验其中的一道题。

【评析：在探索明了小数加法计算方法、自主迁移完善小数减法计算方法的学习后，教师引导学生联系加、减法互为逆运算的关系图式，在运算对比中再次理解小数加、减法的算理，建立起小数加、减法的计算模型。多类别检验方法的追问与回忆，便于学生在更高和更为抽象的层面上理解和把握知识间的联系。】

4.举例归纳，完成建模。

师：刚才研究的小数加、减法（板书课题：笔算小数加法和减法），只探讨了一道加法、一道减法，接下来想怎么研究？

活动：自己做小老师，联系生活出一道不同类别的用小数加、减法解决的题目，同桌交换列竖式计算解决。

师：同学们开动小脑筋，想出了好些不同类别的题目，咱们一起来分享一下（答案折叠起来）。

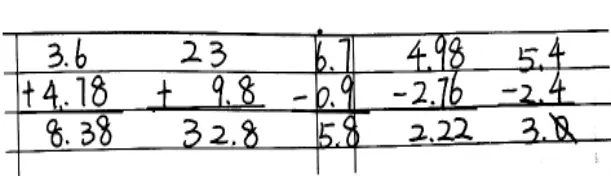
师：看出它们分别是哪个类别了吗？

师：挑选其中的两道，在作业纸上试着做一做。

强调：得数能化简的要化简；整数部分占位的0不能省略；整数在个位的右下角有隐藏的小数点。

【评析：探究——迁移——建模——创编的学习顺序，符合学生旧知转化、图式再创的认知过程。本环节，教师引导学生自编“不同类别”的题目，促发了学生对不同题型的思考；引导其他学生讲述“差异化的类别”、实际操作“其中的两道”……学生在思考与操作中感悟算理、形成算法，自主建立起运算模型，也实现了灵活用模的目标。】

三、灵活运用，深化理解

1.火眼金睛。（小数点位置没对齐、结果末尾的0没去掉、得数整数部分的0没写）

2.想竖式说得数。2.22+0.072.22+0.72.22+7

师：说说看，你的脑海中，哪个数没变，哪个数在变？