拓展高职学生的数学美学教育
潘敏 刘志林


【摘 要】本文以“斐波那契(Fibonacci)数列与黄金分割比”以例,向高职学生渗透数学美学教育。
【关键词】美育;斐波那契数列;黄金分割比
一直以来,在应试教育的压力下,高职学生对数学的普遍感受就是難和枯燥,他们无法领会数学的美,更多的是厌倦。如何改变这一现状,重新激发起学生学习高等数学的兴趣,是每一个高职数学老师面临的问题。笔者通过多年的教学实践,发现如果能让学生感受到数学美,让学生对数学另眼相看,会极大地提高学生学习数学的热情,使得高等数学的学习能够更加轻松,从而让学生感叹,原来数学可以这么美好!本文以“斐波那契(Fibonacci)数列与黄金分割比”以例,向高职学生渗透数学美学教育。由于其中涉及到极限相关运算,可以在讲数列极限运算时引入。
斐波那契数列又称兔子数列,是中世纪意大利数学家莱昂纳多·斐波那契在研究兔子繁殖时提出的,而就是这样一个看似简单的数列却蕴涵着大学问,让我们看到了自然与美。
1、斐波那契数列定义
问题的由来:假设一对新生的兔子需要一个月的时间才成长为成熟的兔子,而一对成熟的兔子每月可以生一对新生的兔子。现有一对新生的兔子,问 N 个月后有多少对兔子?由每月兔子的总数量构成的数列即称为斐波那契数列。
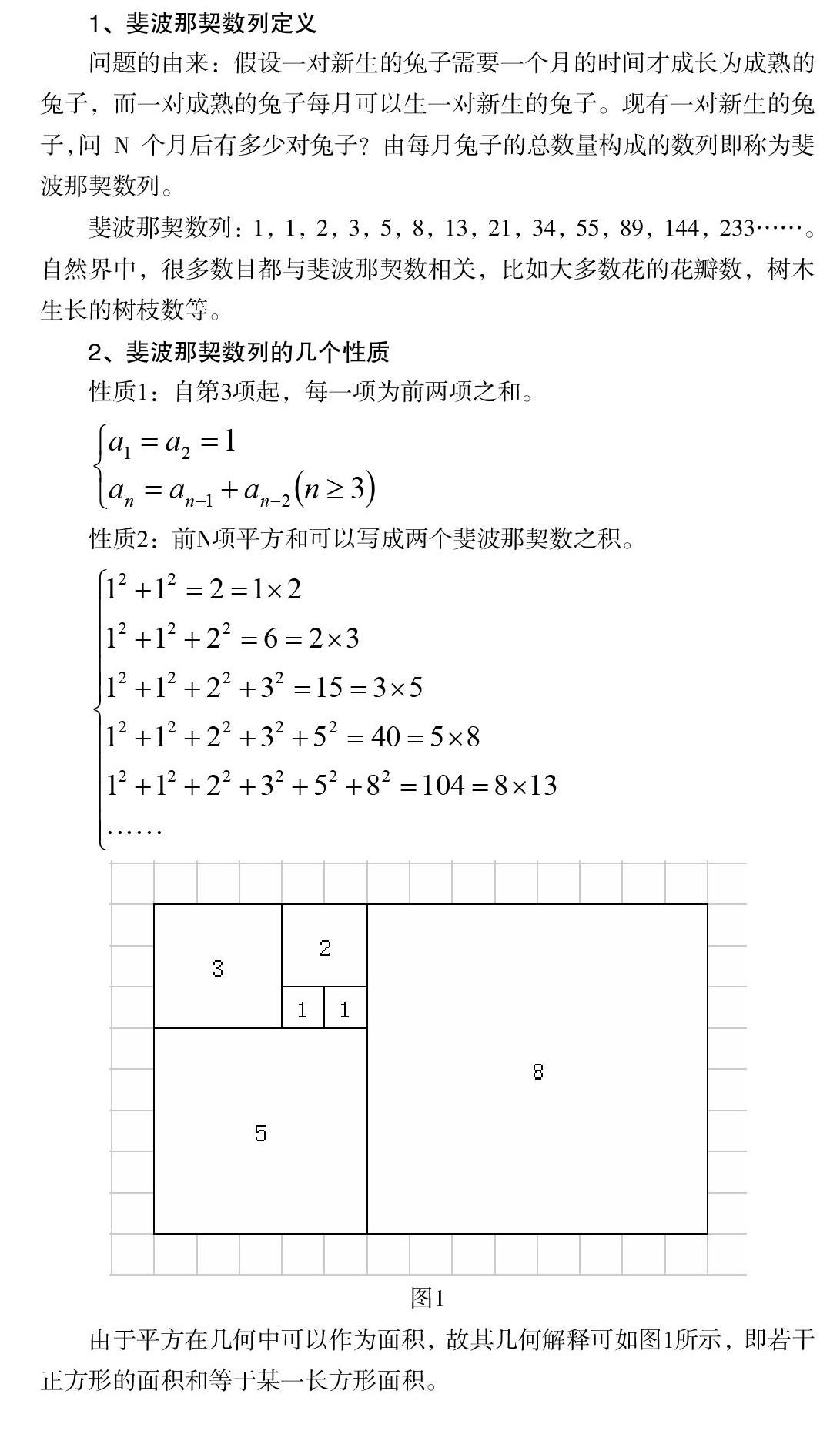
斐波那契数列:1,1,2,3,5,8,13,21,34,55,89,144,233……。自然界中,很多数目都与斐波那契数相关,比如大多数花的花瓣数,树木生长的树枝数等。
4、斐波那契螺旋线
由性质2,可以构造出斐波那契螺旋线(见图2),自然界中存在许多斐波那契螺旋线的图案,比如鹦鹉螺的形状、植物花苞中种子的排列、银河系的构成等,由于具有黄金比例特性,是非常美丽的自然构造。斐波那契螺旋线也称黄金螺旋线,由于其美感,很多艺术设计也是基于黄金螺旋线,比如达芬奇的画、苹果公司Logo的设计、摄影技巧与音乐编曲等。
参考文献:
[1]郭培俊.挖掘数学之美,拓展通识视域[J].浙江工贸职业技术学院学报,2017,17(02):76-79.
作者简介:
潘敏,1984年4月10日出生,女,汉族,江苏泰州,硕士,副教授,高等数学。

