TiAl合金低压涡轮叶片榫头磨削温度场研究*

奚欣欣, 陈 涛, 丁文锋

(南京航空航天大学 机电学院， 南京 210016)

近年来，随着材料性能与工程应用研究取得的进展，TiAl合金逐渐成为“轻质、高强、耐热”材料的典型代表。该类材料的密度(约为4 g/cm3)仅为镍基高温合金的1/2，服役温度比普通钛合金高约200 ℃[1-3]。因此，TiAl合金未来有望被广泛应用于制造航空发动机的重要零部件，如低压涡轮叶片和高压压气机叶片等。GE公司已成功将Ti-48Al-2Cr-2Nb合金应用于其GEnx发动机的第6、7两级低压涡轮叶片，单台发动机质量减轻约90 kg。

由于塑性差、导热系数低和化学性能活泼等原因，TiAl合金被认为是典型的难加工材料。磨削是加工钛合金和高温合金等强韧类难加工材料的重要方法，可以同时获得良好的表面质量和较高的加工精度[4]。研究表明：相比切削加工，TiAl合金塑性差的性能特点对其磨削加工过程的影响较低：在其磨削表面并未发现严重的材料剥离现象[5]。然而，磨削加工过程消耗的能量显著高于切削加工的[6]。若磨削条件选择失当(例如材料去除率过大或切削液供给不足)，极易导致磨削温度过高，引发磨削烧伤。该问题在磨削TiAl合金等强度高、导热系数低的材料时更为突出[7-9]。

在成型磨削过程中，型面的存在导致磨削温度在工件表层的分布更为复杂。MIAO等[10-11]基于有限元分析法研究了刚玉砂轮磨削GH4169枞树形榫齿时的温度分布，最高温度的有限元模拟结果与实测值的误差低于20%，齿顶处的最高磨削温度比齿根处的高约15%～50%。SU等[12]探讨了磨削渐开线齿轮时的温度特征，发现齿面中心区域的最高温度比边缘的高约50%，磨削烧伤主要发生于齿面中心区域。现代商用航空发动机的低压涡轮叶片榫头多为燕尾形，目前少有关于该形状榫头磨削过程中温度分布的报道。

研究拟采用有限元法探索TiAl合金低压涡轮叶片榫头磨削过程中的温度分布特点。第一部分介绍有限元建模的基本方法；第二部分通过与实测温度的对比验证有限元法的合理性；第三部分讨论磨削温度的分布特征，包括型面特征对温度分布的影响和典型位置的最高温度差值等。

1 低压涡轮叶片榫头磨削温度仿真模型

1.1 几何建模和网格划分

试验涉及的TiAl低压涡轮叶片榫头结构如图1所示。实际操作中，几何模型的建立在SolidWorks软件中完成，将生成的.x_t文件导入ANSYS软件用于后续有限元分析。

本试验选用solid70六面体单元进行网格划分。该单元有8个节点，每个节点上都有1个温度自由度。相比四面体单元，采用六面体单元计算温度场的精度较高，并且网格数量较少，计算效率较高。由于工件表层温度梯度大，为兼顾计算效率和精度，采用表层密、里层疏的网格划分方法，如图2所示。

图1 低压涡轮叶片榫头结构Fig. 1 Structure of low-pressure turbine blade tenon图2 几何模型的网格划分Fig. 2 Meshing geometric model

1.2 几何建模和网格划分

磨削过程中，总热流密度qt有4个主要去向：传入工件的热流密度qw、传入砂轮的热流密度qs、切削液导出的热流密度qf以及磨屑带走的热流密度qch[13]，即：

qt=qw+qs+qf+qch

(1)

其中，传入工件的热量比例ε可表示为：

(2)

qt为单位面积承载的热流量。针对磨削过程，可表示为磨削弧区产热的总功率P与磨削弧区面积S的比值：

(3)

其中：Ft表示切向力，vs表示磨削速度，ap表示切深，ds表示砂轮当量直径，lc表示磨削弧区长度，b表示磨削宽度。

LAVINE等[14]将磨料及其裹挟的切削液简化为一种复合材料，提出了计算ε的方法：

(4)

其中:k、ρ和c分别为导热系数、密度和比热容。(kρc)w是工件材料的热接触系数，(kρc)c是复合体的热接触系数。(kρc)c可由式(5)和式(6)获得。下标c、f和g分别代表复合材料、切削液和磨粒，φ是砂轮近表面气孔率，可由文献[15]获取。该方法已被成功用于计算镍基高温合金GH4169磨削过程中传入工件的热量比例[10-12]。

kc=φkf+qs+(1-φ)kg

(5)

(pc)c=φ(pc)f+(1-φ)(pc)g

(6)

传入磨屑的热流密度qch可近似由极限磨屑融化能获得[16]：

(7)

Tm指工件材料熔点，vw指工件进给速度。将式(1)～式(7)合并，可知流入工件的热流密度是：

(8)

发生磨削烧伤处切削液与工件没有直接接触，磨削条件类似于干磨。此时ε可通过式(9)计算[16]：

(9)

此处r0表示磨粒的有效接触半径，其取值可以参考文献[16]。

计算所需的工件材料、切削液和磨粒性能参数总结于表1和表2。

表1 工件材料的热导率k和比热容c

表2 切削液与磨粒的性能参数

1.3 热源选择与加载

热源分布方面，应用较为广泛的有矩形热源和三角形热源等分布模型。本试验选择直角三角形热源模型进行温度仿真，以对应磨粒切削前期热源强度低、后期热源强度高的分布特点[17]。此外，在普通磨削条件下，需在工件四周(底部除外)施加对流换热系数，以表示切削液的冷却作用。ROWE等[16]的研究表明：水基乳化液的对流换热系数为6 700 W/(m2· ℃)。计算时将连续不断的磨削过程离散，以“时间步和子步”进行处理[17]。在本试验中，共分60时间步，步长为工件长度与工件进给速度的比值。

1.4 边界条件设定

本试验涉及的温度场仿真属三维范畴。在求解区域Ω内，瞬态温度场的场变量T(x,y,z,t)在直角坐标中应满足以下热量平衡方程：

(10)

其中：t表示时间；Q(x,y,z,t)表示物体内部的热源密度。等式左边第一项为微分体升温所需要的热量；第二、三、四项分别为x、y、z方向传入微分体的热量；等式右边为微分体内热源产生的热量。

在计算温度场时，应满足三类边界条件：

(1)在Γ1边界上设定温度T(Γ,t)

T=T0

(11)

其中：T0为磨削前的工件温度，设定为20 ℃。

(2)在Γ2边界上设定热流密度q(Γ,t)：

(12)

其中：kx、ky和kz分别表示材料沿x、y和z方向的导热系数；nx、ny和nz为边界外法线的方向余弦。

(3)在Γ3边界上设定对流换热的条件：

(13)

在自然对流和强迫对流条件下，Ta(Γ,t)分别为外界环境温度和边界层的绝热壁温度。

求解区域Ω全部边界Γ应满足：

Γ1+Γ2+Γ3=Γ

(14)

2 仿真合理性验证

工件使用经热等静压的Ti-45Al-2Mn-2Nb-0.1B合金，材料的主要物理/力学性能总结于表3。磨削工艺选择航空发动机低压涡轮叶片榫头常用的缓进深切磨削工艺，使用电镀金刚石砂轮(400 mm×10 mm×127 mm，磨粒粒度为80/100)，磨削方式为顺磨，主要磨削条件见表4。采用K型标准热电偶测量磨削温度。

表3 Ti-45Al-2Mn-2Nb-0.1B合金性能

表4 仿真结果验证试验的主要磨削条件

叶片榫头位置Ⅰ和位置Ⅱ的最高磨削温度的仿真和试验对比结果如图3所示。仿真结果与实测值之间的误差约为15%，说明采用上述有限元法可以用于分析TiAl合金低压涡轮叶片榫头磨削温度场特征。

(a) 测量位置 Tested position(b)ap=0.5 mm(c) ap=1.2 mm图3 最高磨削温度的仿真与试验结果对比 Fig. 3 Comparison between simulated and experimental results of maximum grinding temperature

3 磨削温度分布的结果与讨论

3.1 磨削表面的温度分布

不同时间步的磨削表面温度分布如图4所示。随着时间步的递增，最高温度逐渐增大。在不同磨削条件，第1个时间步后磨削表面的最高温度仅为54.3 ℃和367.9 ℃，第30个时间步后则分别上升至106.6 ℃和818.2 ℃。该结果与MALKIN等[15]总结的缓进深切磨削温度的变化规律相一致，即最高磨削温度需要一定的时间/磨削路程才能到达稳定状态。

(a)ap=0.5 mm,时间步1ap=0.5 mm, Time step 1(b)ap=1.2 mm,时间步1ap=1.2 mm, Time step 1(c) ap=0.5 mm,时间步4ap=0.5 mm, Time step 4(d)ap=1.2 mm,时间步4ap=1.2 mm, Time step 4(e) ap=0.5 mm,时间步30ap=0.5 mm, Time step 30(f)ap=1.2 mm,时间步30ap=1.2 mm, Time step 30图4 磨削表面的温度分布 Fig. 4 Temperature distribution on ground surface

以磨削切入端的齿顶圆弧中心处为起点，沿磨削方向不同距离l处的磨削温度随时间变化的规律如图5所示。可以认为，在距离起点约7 mm处，最高磨削温度到达稳定状态。这同时说明，在采用有限元法模拟磨削温度时，工件长度应设置在该值以上。

(a)ap=0.5 mm(c) ap=1.2 mm图5 齿顶区域不同位置温度对时间的响应 Fig. 5 Temperature response to grinding time on different positions on top of tenon teeth

3.2 横截面磨削温度分布

成型磨削时工件内部的温度分布较为复杂，尤其是叶片榫头等复杂结构。工件内部的温度分布可通过横截面反应，如图6所示。图6中：在工件表层，最高温度出现在圆弧形榫齿的齿顶位置，接近榫齿对称轴线的位置温度较低，右侧齿底位置的温度则介于二者之间；榫头下半部分基本不受影响。产生这一温度分布特征的原因在于，在榫齿顶部，热量多数在齿顶内部传导。换言之，在该区域内单位体积工件材料承载的热流密度较高。齿根部的热量则可以传导至榫头下半部。

(a)ap=0.5 mm(b)ap=1.2 mm图6 工件材料内部的温度分布 Fig. 6 Temperature distribution in workpiece material

磨削温度可传导至表面以下一定深度，在表层形成“热影响区”。过高的磨削温度可能对表面完整性产生不利影响，催生白层、残余拉应力和微观裂纹。有限元法可以输出不同深度的温度值，结合诱发上述问题的临界温度，理论上可以预测磨削热影响的程度。位置Ⅰ不同深度d的最高温度如图7所示。

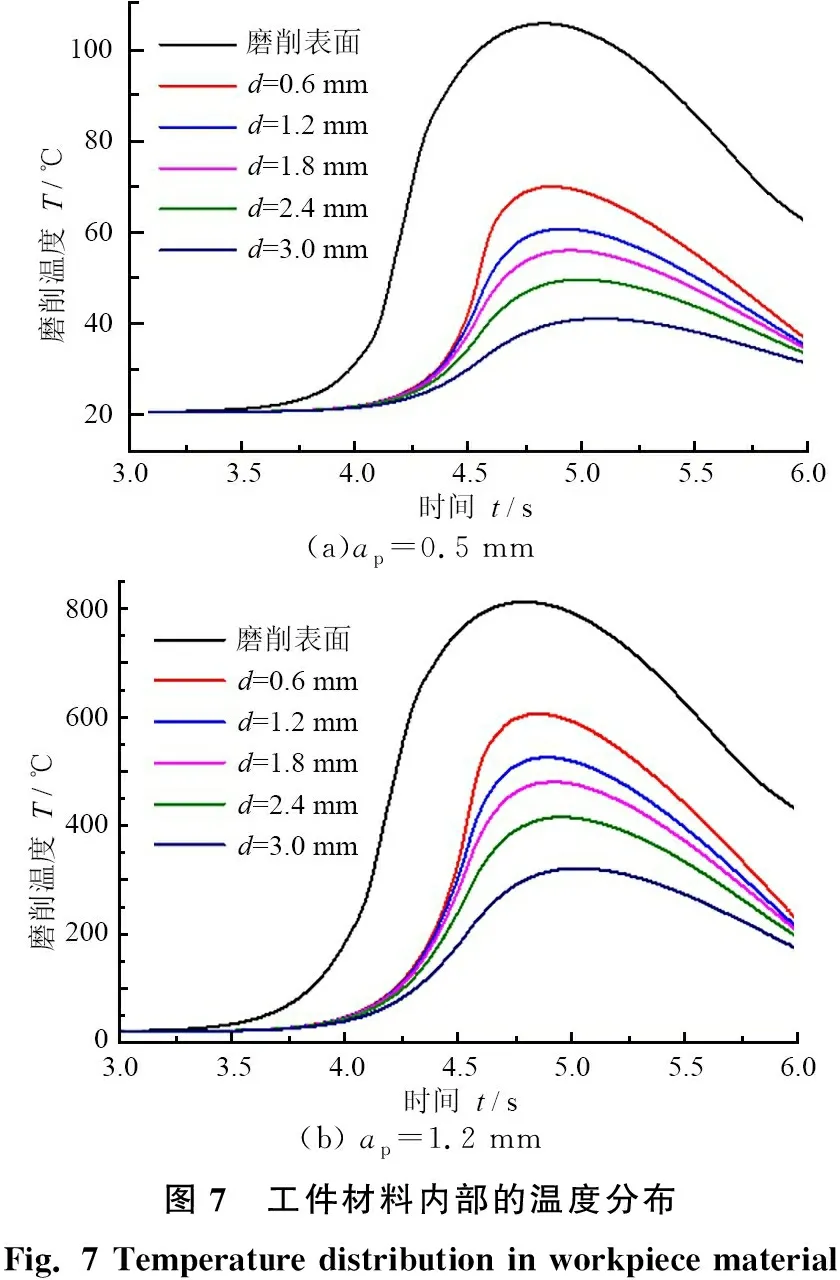
(a)ap=0.5 mm(b) ap=1.2 mm图7 工件材料内部的温度分布 Fig. 7 Temperature distribution in workpiece material

图7中，ap=0.5 mm和1.2 mm对应的磨削表面最高温度分别为107 ℃和818 ℃；在表面0.6 mm以下分别下降至70 ℃和608 ℃；在表面3.0 mm以下进一步下降至40 ℃和324 ℃。

3.3 横截面磨削温度分布

磨削用量对最高磨削温度的影响如图8所示。最高磨削温度随磨削速度、工件进给速度和切削深度的增大而升高。加快磨削速度可使工件材料被分割得更细，磨削过程中的滑擦和耕犁增多，因此磨削温度升高。切削深度增大时，磨削过程中的磨屑变形力和摩擦力均增大，因此磨削能耗增大，磨削温度升高。工件进给速度增大时，热源强度增大，但其在工件表面上的移动速度变快[13]。图8的结果表明：齿顶对磨削温度的增大效果强于齿根对其的减弱效果。在本试验的条件下，位置Ⅰ与位置Ⅱ的温度差异为30%～40%。

(a)磨削速度 Grinding speed(b) 切深 Depth of cut(c) 工件进给速度 Workpiece infeed speed图8 最高磨削温度随磨削用量的变化 Fig. 8 Changes in maximum temperature as function of grinding parameters

4 结论

(1)探索了基于有限元仿真模拟TiAl合金低压涡轮叶片榫头磨削温度的可行性。最高磨削温度的仿真与试验结果差异约15%。该方法可用于预测低压涡轮叶片榫头磨削温度分布和热影响区深度等。

(2)最高磨削温度随磨削的行进逐渐增大，在距离起点约7 mm处到达稳定状态。

(3)磨削温度随磨削速度、工件进给速度和切深增大而增大。由于齿顶处的热传导条件较为恶劣，因此最高磨削温度高于其他位置。在本文涉及的磨削条件下，其值比齿根处高约30%～40%。